公交停靠站区域长度优化研究

宫克，罗钿

（1.长安大学汽车学院，陕西 西安 710064；2.兰州工业学院汽车工程学院，甘肃 兰州 730050）

引言

公交停靠站的区域长度是衡量公交停靠站通行能力的重要指标。公交停靠站的区域长度对停靠站的通行能力和泊位的有效利用率都具有重要的影响。

对于公交停靠站区域长度的取值，若公交停靠站的区域长度过短，则到达停靠站的公交车辆必须在站外等候排队进站。尤其在距离信号交叉口较近的停靠站，还会降低交叉口通行能力及公交停靠站的通行能力。在这种情况下，不仅会造成乘客等待公交出行的时间成本增加，还会降低社会车辆和与之受影响的其他交通工具的运行效率；反之，若公交停靠站区域设计长度过长，虽然从理论上提高了公交停靠站的通行能力，但造成公交车辆无序进站停靠，停靠站的实际通行能力并不随停靠区域长度的增加而增加，公交停靠站的有效使用效率降低，浪费用地，增加停靠站成本，无形中造成不必要的浪费。

1 公交停靠站区域长度分析基本思路

确定公交停靠站区域长度时，通常有以下两种思路：

第一种思路：公交停靠站区域长度直接影响公交停靠站通行能力，对于需要新建的停靠站，可以先计算或预测出站点的通行能力，根据通行能力，确定满足需求的公交停靠站泊位数，以确定停靠站的区域长度[1]；对于需要改建的站点，先计算现有公交停靠站泊位数所能提供的通行能力，将其与此站点实际公交流量比较，从而可知现有站点公交停靠的区域长度能否满足需求。

第二种思路：公交车到站规律近似服从何种分布，服务时间的规律，研究公交车辆在某时间段内的排队长度和满足停靠需求的缓冲空间。这两个参数作为确定停靠站的区域长度的重要依据。

2 基于车辆到达的停靠站区域长度模型

2.1 平均排队长度

步骤1：每辆车到达时的排队车辆数确定

根据马尔可夫理论，定义泊位上的公交车辆离开的瞬时时刻作为一个再生点，两个连续再生点间的时间间隔为一个周期[2]。

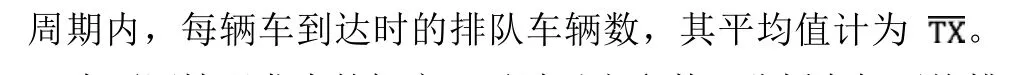
对以下五种情况进行分析：

情形1：第n个周期之初和之末，停靠站区域内无排队车辆。在该种情况下，第 n个周期内无车辆排队，即i=j=0,TX=0。

情形2：第n个周期之初，有i辆车排队等候，且排队车辆不超过泊位数。但在该周期末，系统内车辆全部清空，即 i≤c，TX=0。

情形3：在第n个周期之初无排队车辆，但在该周期末，进入系统的车辆未清空，有 j辆车排队等候出站，即i=0,j>0,TX=j。

情形4：第n个周期之初，i辆车排队等候，等待车辆数不超过泊位数；该周期末排队车辆未清空，仍有j辆车排队。在该种情况下，整个周期内，停靠站满负荷；当c-i车辆到达时，所有未满泊位占满，第c-i+1辆车等待服务。j-1辆车依次排队形成从1到j-1的长队列，即：

情形5：第n个周期之初，i辆车排队等候，且排队车辆数大于泊位数；该周期末，仍有j辆车排队且j≥i-c＞0。在这种情况下，第 i-c辆车仍然滞留在队列进口处，后续到达车辆依次形成i-c，i-c+1，…，j-1的序列，即：

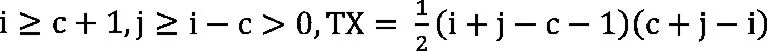
步骤2：转移概率Pij的确定

理想状态下，不考虑城市道路的交通情况、信号交叉路口等因素的影响，按照发车时刻表，公交车辆会以确定的时间间隔均匀到达每个公交停靠站。高峰时段，到达时刻处于不可接受间隙期间。该情况下，到达车辆必须等待可接受间隙之间的车辆通过后，可接受间隙出现时方可通过。此时，车辆间相互影响比较微弱时，因而路段交通流可以近似采用泊松分布加以描述[3][4]。

根据假设条件，车辆的到达过程满足泊松过程，在停靠站内的停留时间满足定长分布，五种不同情形的概率为：

当泊位数C一定，则取决于五种情形的i、j、TXn。因此，通过加权平均的方法获得：

步骤3：平均排队长度的确定

c—泊位数(个)；

dv—公交车辆长度(m)；

ds—停靠站内公交车辆的安全距离 (m)，为了保证公交车辆在站内停靠的安全性，站内公交车辆之间的安全距离通常为3米[5]。

对于港湾式停靠站，要考虑加速渐变段与减速渐变段长度。由运动学知识，渐变加速段和渐变减速段的计算公式为

[6]：

渐变加速段长度为：

d—公交车辆进出站的减速度(m/s2)；

VT—公交车辆通过速度（m/s）；

VT—公交车辆站内速度（m/s）。

步骤5：参数的标定

（1）λT的确定

λ为高峰时段公交车辆的到达率，辆/秒；T为确定的单位时间，s。λT—T时间内，到达的平均车辆数。

将在目标停靠站采集到的实际数据进行换算，可通过以下公式计算：

Q为实际调查每小时车流量，pcu/h。

（2）最大到达车辆数Qn的确定

设车辆到达过程服从泊松过程，设Tn为第n个周期的时间，KTn为第n个周期内到达的车辆数。因此，

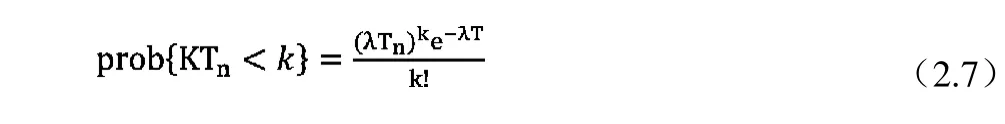
其中，λ-高峰时段车辆的到达率，辆/秒；λT—第n个周期内到达的平均车辆数。

假设置信概率为α，则在车辆在 Tn内的最大车辆数为Qn。由此可知：

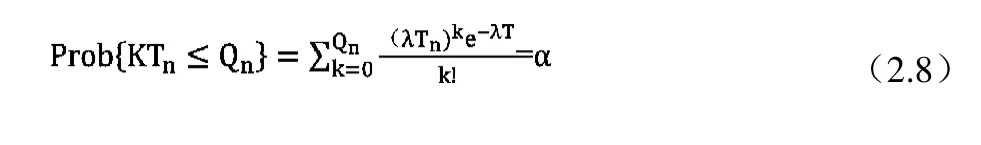
3 实例分析

车辆到达服从泊松到达过程，取置信概率为α=0.997，则在车辆时间T内的最大车辆数为Qn。由公式2.8知，在周期内最大到达车辆数Qn=5。通过公式2.1得：

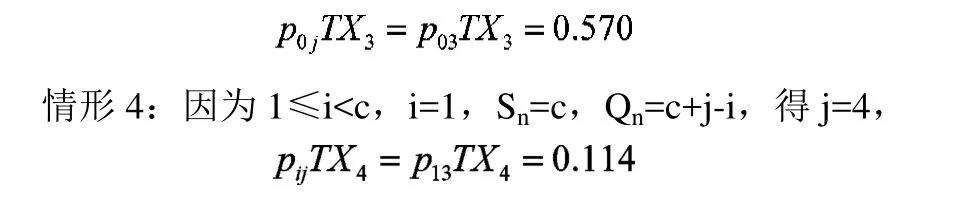
（3）情形 5：i≥c，即 i≥c 且 j≥i-c＞0。

i为周期之初排队的车辆数，此时可通过第n-1个周期末滞留的车辆数得出。

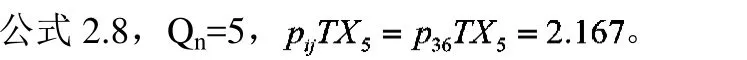
为了满足公交停靠站线路容量和停靠要求，根据高峰时段确定的平均排队车辆数，翠华路公交停靠站的区域长度至少要满足三辆车同时在站时的长度。

对于直线式公交停靠站的区域长度为车辆平均排队长度与停靠站内公交车辆间的安全距离相加。为了研究的统一性和合理性，以便在VISSIM仿真过程中参数的标定和统计结果的分析。因此，取VISSIM仿真软件公交车辆的长度默认值11.54m，停靠站内公交车辆之间的安全距离通常取为3米。因此，VISSIM 仿真软件，该公交停靠站的区域长度应该设置为43.62m。

4 VISSIM仿真分析

4.1 基本参数的确定

4.1.1 基本交通状况

陕西省西安市雁塔区小寨东路连接小寨商圈与大雁塔旅游区，小寨东路的翠华路站位于翠华路与小寨东路交叉口上游55m处，北临陕西省历史博物馆。小寨东路与翠华路交叉口所在道路情况：北进口道路为双向四车道，单车道宽度为3.5m；东、西、南进口道路均为双向六车道，单车道宽度为3.5m。

小寨东路翠华路公交停靠站距离下行方向的人行横道35.6m。在调查区域内和时间内，无社会车辆停靠和非机动车停靠。路面平整、坡度符合设计要求[10]。停靠站形式为直线式，区域长度24m，设计泊位2个。

4.1.2 公交车高峰时段的发车间隔及清空时间

通过对小寨东路翠华路公交站的实际调查情况可知，高峰时段车辆的到达密度较大。因此，考虑到数据的准确性，调查该停靠站所在的上游交叉口的信号周期为120s。因此，在车辆时间间隔的调查过程中，以120s作为一个时间单位，记录相继到达停靠站公交车辆的时间。记录早高峰（7：30-8：30）和晚高峰（18:0 0-19:00）这两个高峰时段的同线路公交车的到达时间，然后计算相继到达的同线路公交到达时间的间隔，求多组数据的平均值。通过对翠华路停靠站的实际调查，12条公交线路的公交车辆在高峰时段公交车辆的平均到达间隔为△T=17s。

清空时间由公交车辆启动和行驶出停靠泊位的时间和公交车辆重新汇入车道的等候时间之和确定。通过实际的观测值，该值在9s-20s之间[2]。对于直线式停靠站，不计入公交车辆重新汇入车流的等待时间。因此，在翠华路站的仿真参数的设定中，清空时间TC=15s。

通过实际情况的调查，翠华路站现有区域长度设置为24m。在线路容量、车流量、公交车发车间隔、公交车站内清空时间等参数不变的情况下，将直线式停靠站改建为港湾式停靠站。VISSIM软件中默认车辆速度分布为30-35km/h，市内公交停靠站内的速度为 13-23km/h[10]。因此，确定停靠站停靠区域长度为36m。

4.2 仿真结果分析

4.2.1 排队长度对比分析

模型结果的仿真结果：随着仿真时间的增加，数据稳定性会更好；对于上游排队检测器，1800-4800s仿真时间内，平均排队长度为仅为 2m。公交车辆对于整个停靠站系统的负荷较小；对于下游排队检测器，1800-4800s仿真时间内，平均排队长度为27m。通过马尔可夫模型的计算结果，该停靠站的设计泊位数为3个。

针对实际情况，通过VISSIM仿真，可得到以下结论：实际情况的仿真结果，上游排队检测器，2400-4200s仿真时间内，平均排队长度为66m，最大排队长度为97m。因此，车辆在停靠站区域进口处会出现排队现象；对于下游排队检测器，3000-4800s仿真时间内，平均排队长度为48m，最大排队长度53m。实际情况下，该停靠站的设计泊位数为2个。因此，该停靠站的设计通行能力不能满足高峰时段的车流量需求。

针对改建方案的仿真结果：对于上游排队检测器，1200-4800s仿真时间内，最大排队长度为 98m。因此，车辆在区域进口处会出现排队现象；对于下游排队检测器，3000-4800s仿真时间内，平均排队长度为44m，最大排队长度55m。改建方案，该停靠站的设计泊位数为2个。因此，该停靠站的设计通行能力不能满足高峰时段的车流量需求。

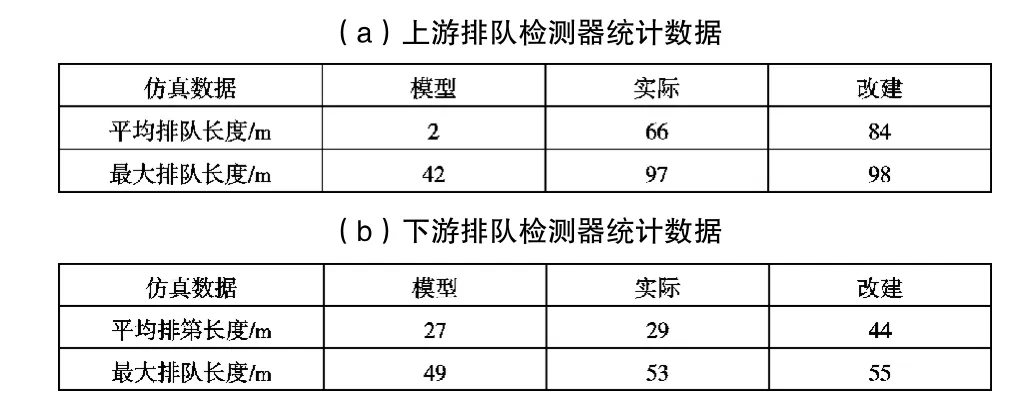
表 1 3600s仿真时间长度对比分析

3600s的仿真数据较为平稳。因此，取3600s仿真时间，分析三个仿真结果由图1所示。

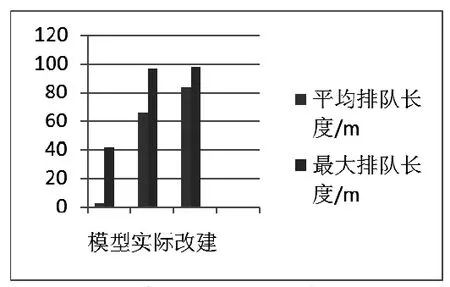
图1 3600s仿真时间内上游检测器排队长度对比

如图1上游排队检测器的检测数据中，平均排队长度和最大排队长度反映了该公交停靠站区域进口处车辆的排队情况和通行能力。基于马尔可夫区域长度的模型优势最为明显。相比于其他两个方案，平均排队长度和最大排队长度最小。

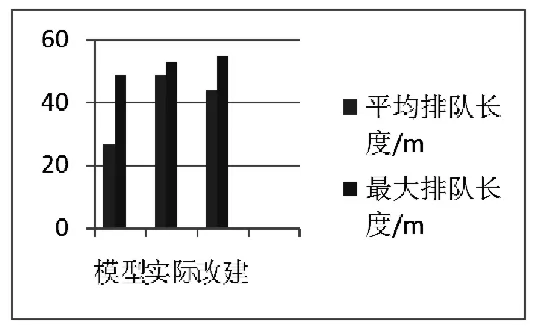
图2 3600s仿真时间内下游检测器排队长度对比图

如图 2，下游排队计数器采集到的数据中，平均排队长度和最大排队长度反映了停靠站区域内的车辆排队情况和通行能力。基于马尔可夫区域长度的模型优势最为明显。相比于其他两个方案，平均排队长度和最大排队长度最小。

4.2.2 公交车延误分析

随仿真时间的增加，公交车延误、平均停车时间和停车次数的数据稳定性愈好。根据调查，公交车的清空时间通常为9-20s，模型仿真结果得出的公交车的平均停车时间小于清空时间。

根据延误最小原则，随仿真时间的变化，基于马尔可夫的停靠站区域长度模型的公交车总延误最小。若将目前的直线式停靠站改为港湾式停靠站，公交总延误较大。因此，就缩短延误时间而言，基于马尔可夫的停靠站区域长度模型有较大的优越性，如图3。

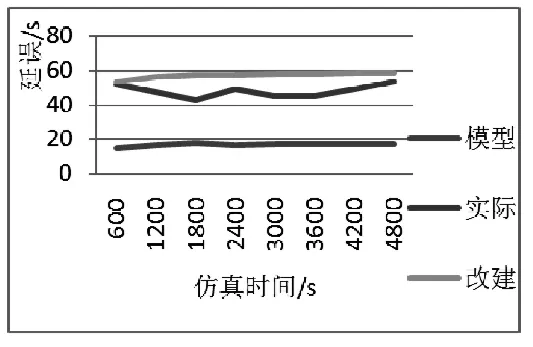
图3 公交车辆延误时间对比

同样的，仿真时间3600s的数据稳定性较好，公交车延误、平均停车时间、平均停车次数以及行程时间内的通过车辆数对比分析。

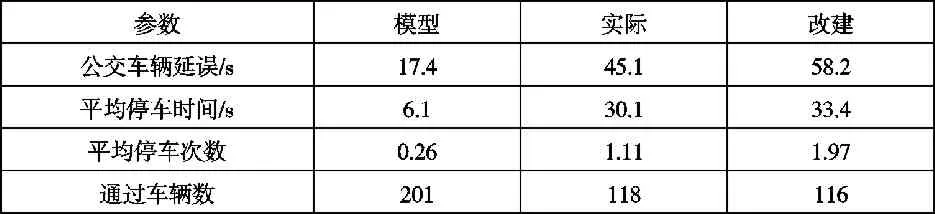
表2 3600s仿真时间内的延误对比

从表2可知，在3600s仿真时间内，对应的停靠站区域长度，基于马尔可夫的停靠站区域长度模型得出的仿真结果中，公交车延误与平均停车时间最短，平均停车次数最少，相同时间内通过的车辆数最多。

4.3 优化方案的选择

通过对马尔可夫模型、实际情况和改建模型的仿真结果，马尔可夫模型得出的结果相比于其他两个方案，平均排队长度和最大排队长度较低小，延误时间的值都较低。所以，基于马尔可夫的停靠站区域长度模型的对于确定停靠站的区域长度有明显的优越性。

将24m直线式停靠站改建为36m港湾式停靠站是不合理的，排队长度增加，且延误也随之增加，用地面积增加，对路段通行能力造成较大的负荷。

对于翠华路停靠站，最优的选择方案为将现有区域长度增加为43.62m，不需要改变现有的设施，只需划定该区域范围，通过道路标志标牌明确在高峰时段，该区域内，不允许社会车辆停靠；在平峰时段，则不做限制。因此，该种方案是具有较强的可行性，且最大程度上节约用地，改建成本较低。

5 结语

运用VISSIM仿真软件，对典型的公交停靠站进行改造方案仿真分析，通过平均排队长度、最大排队长度以及公交车辆的延误等统计结果，确定合理的改造方案，优化现有的停靠站区域长度。验证马尔可夫模型在确定停靠站区域长度的可行性及合理性。

参考文献

[1] 何赟.多线路公交停靠站站址与站位问题研究[D] .成都:西南交通大学,2011

[2] Sheldon M .ROSS. Introduction to Probability Models[M]. 2010

[3] Akcelik R, Chung E.Calibration of the bunched exponential distribu-tion of arrival headways[J]. Transport Research,1994, （3）: 42-59.

[4] 肖和华,张显尊等.公交停靠站设置形优化选择研究[J]交通工程2011.9(18):45-50

[5] 建设部.中华人民共和国行业标准—城市道路设计规范CJJ37-90.北京:中国建筑工业出版社,1991

[6] 吕林.城市公交停靠站优化设计方法研究[D].南京:东南大学,2006.

[7] Fernández, R., 2007. Passion 5.0-a model for microscopic simulation of multiple-berth bus stops. Traf fi c Engineering and Control 48 (7),324-328.

[8] Basso, L. J. and H. E. Silva (2010). A microeconomic analysis of congestion management policies. 5th Kuhmo Nectar Conference in Transport Economics Valencia, Spain, July 8-9.

[9] Alejandro Tirachini. The economics and engineering of bus stops:Spacing, design and congestion[R]. The University of Sydney ,May 2012.

[10] 王炜,杨新苗,陈学武.城市公共交通系统规划方法与管理技术.北京:科学出版社,2002.

[11] 李静涛.基于 VISSIM 仿真的公交港湾式车站设置条件研究[D].石家庄:石家庄铁道学院,2010.