基于改进CPSO算法的含随机负荷配电网重构

徐文彬， 马立新

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

配电网重构技术是通过改变配电网络线路中不同的联络开关与分段开关来改变网络的拓扑结构，同时在满足配电网潮流约束和配电网辐射状运行等要求的约束下，使配电网线损、供电质量、负荷均衡度等指标达到最优的运行方式。近年来，分布式能源以及电动汽车发展迅速，其经济性、环保性的特点也越来越受到重视，必将得到更广泛的应用[1-2]。

针对分布式能源的接入以及随机负荷的影响下，如何提高配电网的效益，文献[3]在综合考虑降低网络损耗和开关操作的问题下，导出不影响结果的必选支路，改进遗传算法中的编码方式，再结合最优潮流计算，提高计算效率并求出最优解；文献[4]将网损、购买DG的电能费用和配电网优化获得的收益分配给用户的费用相结合，利用改进量子进化算法进行综合优化重构；文献[5]提出了基于粒子群算法的配电网重构同时考虑分布式能源接入的综合优化算法。但上述研究都还存在一些问题：未考虑日益增多的电动汽车等随机性负荷的影响；大多数研究对分布式能源以及负荷随机性对配电网重构问题的影响考虑不够充分。

本文将结合风光以及电动汽车这类随机负荷的特点，分析其分布特性，拟合出负荷曲线，再以风光电购入成本，电动汽车的充放电成本以及网络损耗的成本之和为目标函数建立模型，最后根据所提出的改进混沌粒子群对所建立模型进行优化求解。

1 建立模型

1.1 目标函数

本文以一天24 h为计算周期，综合分析了配电网的网络损耗成本，风光电的购入成本以及电动汽车的充放电成本，结合配电网运行时的潮流约束，辐射运行等约束条件，建立重构模型，并求解最优的重构方案。配电网分时重构的数学模型为：

minf=min(f1+f2+f3+f4)

(1)

(2)

(3)

(4)

(5)

式中：f为综合费用；f1为配电网网损的经济损失费用；f2为风力发电的购入成本；f3为光伏发电的购入成本；f4为电动汽车的随机充放电成本；T,N1,N2分别为时段数，支路数，电动汽车数量；Pwind,Ppv,Pout,Pin分别为购入的风电功率，光伏发电功率，电动汽车的放电功率与充电功率；c1,c2,c3,cout,cin分别为市电价格，风电与光伏的购入价格，以及电动汽车的充放电价格。

1.2 约束条件

(1)潮流约束：

(6)

(7)

式中：Pi,Qi为节点输入功率；PDG,QDG为风光和电动汽车的注入功率；Pli,Qli为负荷的功率；Vi,Vj为节点电压；Y为支路导纳矩阵。

(2)支路电流约束：

Iimin≤Ii,t≤Iimax

(3)节点电压约束:

Vimin≤Vt,i≤Vimax

(4)无孤岛且网络呈辐射状运行。

2 不确定因素模拟

2.1 光伏阵列

光伏阵列的发电功率主要受太阳辐射强度影响。假设太阳光照幅度服从N(μ,σ2)的正态分布。光伏阵列的输出功率Ppv随太阳辐射强度的关系为[8]：

(8)

式中：Ypv为光伏电板的额定功率;fpv为降低处理系数；GT为当前时间步长上光伏组件的平均太阳辐射量；GT.STC为标准测试条件下的入射幅值(1 km/m2)；αp为温度影响系数；TC为光伏组件的温度；TC,STC为标准测试温度(25 ℃)。

2.2 风电机组

风电机组的发电功率主要与风速有关，假设风速情况服从w(k,c)的韦布尔分布。风电机组的输出功率Pw与风速v变化的关系为[9]：

煤泥水处理系统见图1。精煤、中煤和矸石筛筛下水先经浓缩旋流器组截粗浓缩。旋流器底流经弧形筛、高频筛脱水后进入洗混煤，溢流进一段浓缩机。一段浓缩机的底流由5台沉降过滤式离心机回收后掺入洗混煤，离心机的离心液返回二段浓缩机。二段浓缩机的底流进入压滤机，压滤煤泥直接销售。一段和二段浓缩机的溢流用作循环水。

(9)

式中：vci为切入风速；vr为额定风速；vco为切出风速；Pr为风力发电机的额定输出功率；a,b均为常系数，a=Prvci/(vci-vr),b=Pr/(vr-vci)。

2.3 电动汽车

文献[7]对电动汽车的充放电行为进行了详细的研究。随着共享电动汽车的日益发展，上海地区已经在相当大的范围投入使用，本文在此基础上，将电动汽车分为3个类型：公交车，私家车，租赁车。

公交车与私家车的时间都比较固定，租赁车作为新兴的共享交通，大大地提高了人们出行的便利性。租赁车的随机性较大，除开有人租赁的时间外，其余时间都在固定充电桩上，充放电时间都较为充裕。

根据电动汽车的特性，利用蒙特卡罗模拟法拟合出不同类型电动汽车的充放电负荷曲线。

3 基于改进混沌粒子群的分布式能源配电网重构

粒子群算法源于鸟类觅食的过程。每个粒子通过计算迭代过程中个体最好和群体最好的评价值来跟新粒子的速度和位置，跟新公式为：

vk+1=wvk+c1(pbestk-xk)+c2(gbestk-xk)

(10)

xk+1=xk+avk

(11)

式中：xk与vk对应每个粒子当前的位置与速度；xk+1与vk+1对应每个粒子下一时刻的位置与速度；粒子位置与速度的取值范围分别为[Xmin,Xmax]、[Vmin,Vmax]；若迭代中位置和速度超过边界则取边界值。pbestk与gbestk对应个体最好位置和群体最好位置的评价值；w为粒子的惯性权重；c1与c2对应粒子的学习因子；a为约束因子。

3.1 混沌粒子群原理

混沌算法具有随机性、便利性、敏感性等特点，在算法陷入局部最优时，可以通过引入混沌思想，使之跳出局部极值，其粒子的移动原理图如图1所示。混沌优化算法的思想是将变量从混沌空间变换到解空间，然后进行搜索，本文中采用Logistic映射构造混沌序列：

xn+1=μxn(1-xn)

(12)

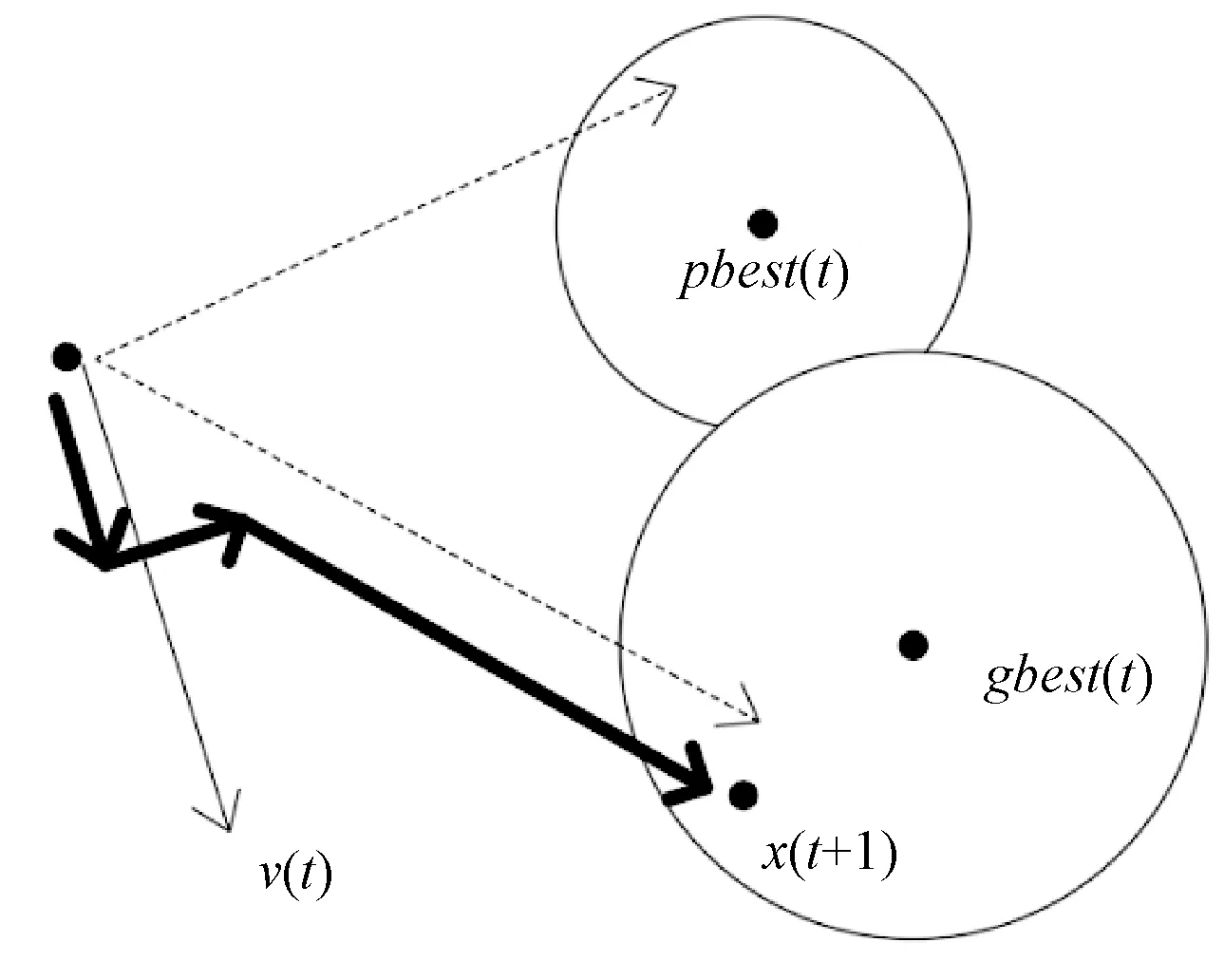
图1 粒子的移动原理图

3.2 改进混沌粒子群算法

本文采用IEEE33节点配电网络进行分析，为减少无用的重复解，加快算法的就算速度，首先对网络进行简化[10]，如图2所示。

随着迭代过程的逐步增加，粒子的速度信息的变化程度会越来越小，种群中的粒子会出现大量聚集的状况，使得算法陷入了局部最优。因此为了避免或减缓这种情况的发生，本文引入了变异算子，赋予每个粒子变异能力，是每个粒子在大量聚集时，变异产生新的位置，从而向着实际最优解的方向运动，变异公式为：

(13)

式中：Gaussi(t)为高斯函数。

将改进CSPO算法与本文结合，先随机初始化粒子群的位置与速度，粒子群向量x是由配电网中的开光状态构成的0～1数组，在5个环路中分别选择一个开关断开，同时满足配网运行的各种约束条件，并在数组中用0表示断开，1表示闭合。后续根据式(10)(11)跟新粒子的速度和位置。

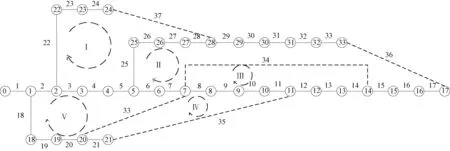
图2 IEEE33节点系统图

改进混沌粒子群算法流程图计算配电网动态分时重构的流程图如图3所示。

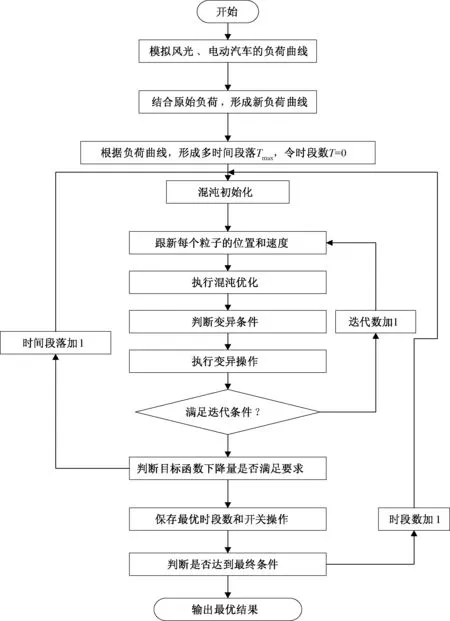
图3 基于改进混沌粒子群的配电网分时重构流程图

4 算例分析

本文以IEEE33节点配电系统进行算例分析。在节点7,18,24分别接入风电机组，光伏阵列和电动汽车。具体参数如下：

(1) 风电机组的额定功率为1 MW，额定风速为14 m/s，切入切出风速分别为4 m/s，25 m/s。根据上海某地一天的风速信息和太阳辐照度信息得到的风光发电功率如图4、5所示。

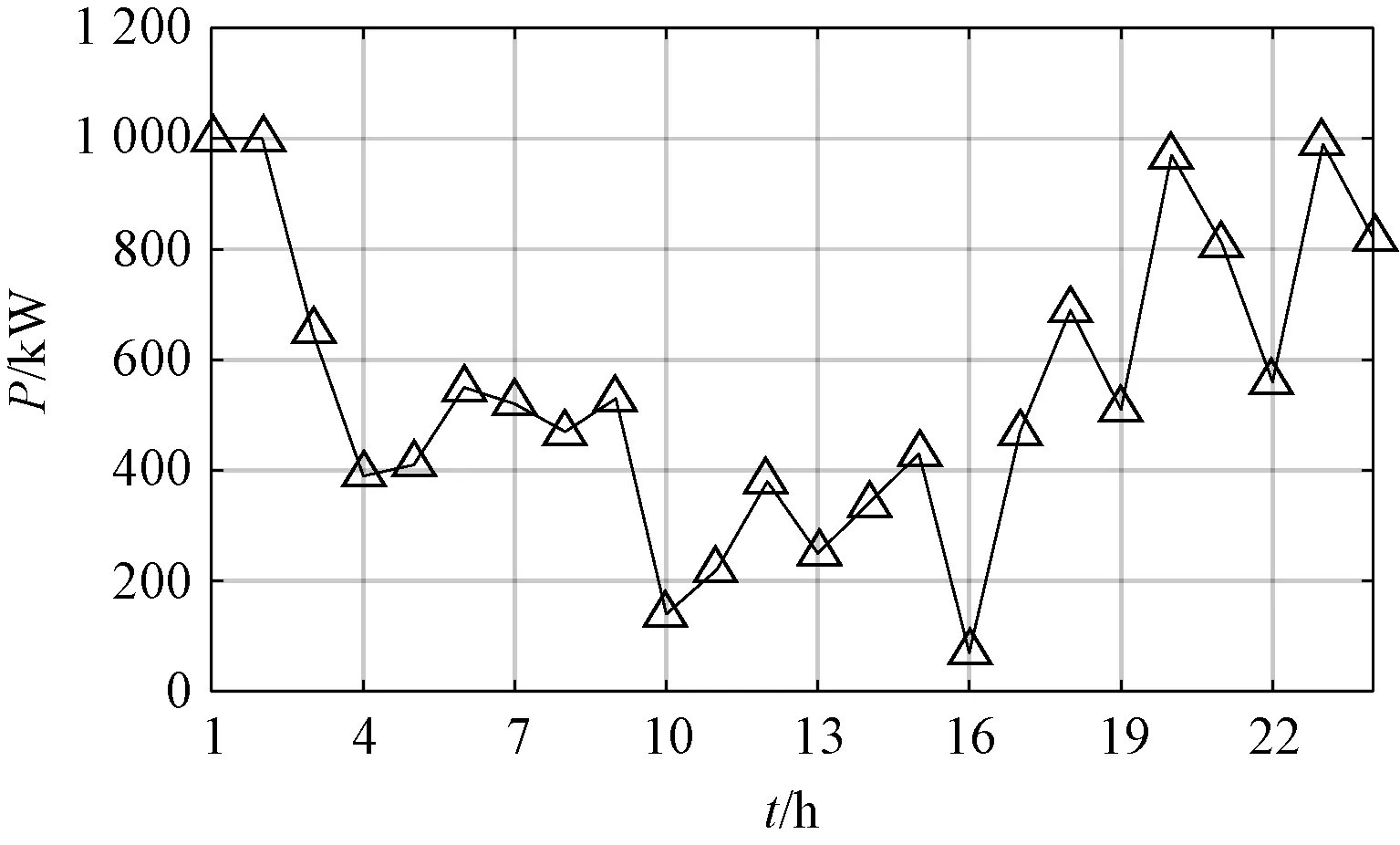
图4 风力发电功率曲线

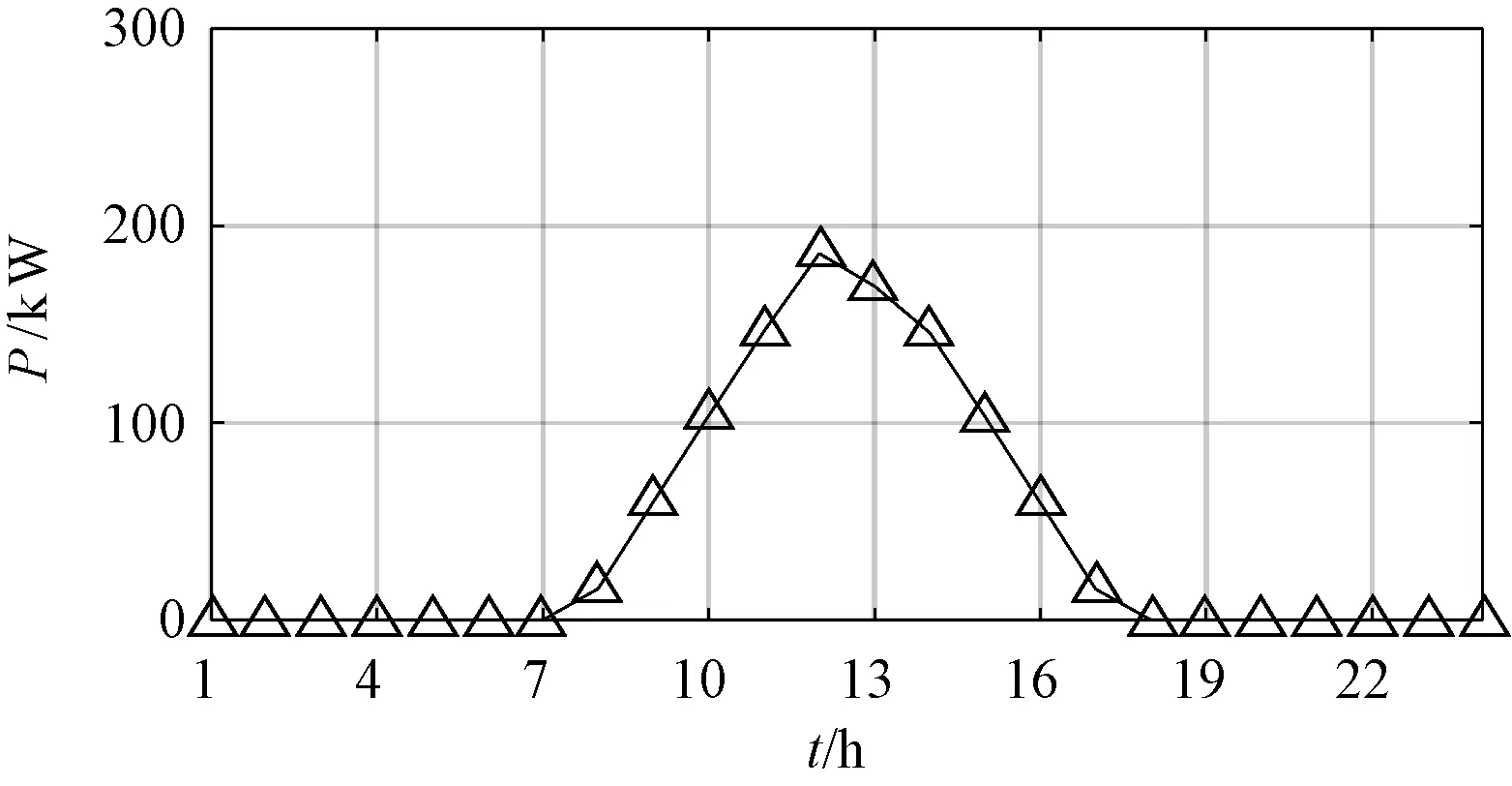
图5 光伏发电功率曲线

(2)本文对于电动汽车的模拟参考的是文献[7]的相关方案，电动汽车共有租赁车、公交车和私家车3种类别，投入比例为2∶3∶5。假设总共投入了500辆电动汽车，利用蒙特卡洛模拟法拟合出的电动汽车充放电负荷如图6所示。

图6 电动汽车充放电负荷曲线

改进混沌粒子群算法和粒子群算法中参数都设置为：粒子数N=20；惯性权重系数w=0.8；加速系数c1=c2=2；粒子速度Vmax=4，Vmin=-4；迭代次数为100次。

将风光电功率和拟合出的电动汽车充放电负荷与原始负荷数据相结合，原始负荷采用上海某地区的负荷数据采用上述提到的改进混沌粒子群算法对含有风光的配电网分时动态重构模型进行求解，并将求得的结果与粒子群算法的结果作比较[11]。

由表1、2的结果可以看到，对包含风光发电以及电动汽车的配电网络进行分时段动态重构之后，一天的综合成本得到了明显的优化，同时将本文的改进混沌粒子群算法与粒子群算法进行比较之后，可以看出本文所用的改进混沌粒子群算法，能够获得比粒子群算法更好的重构结果，降低了优化成本，且总开关次数也有所降低，减少了不必要的开关成本。

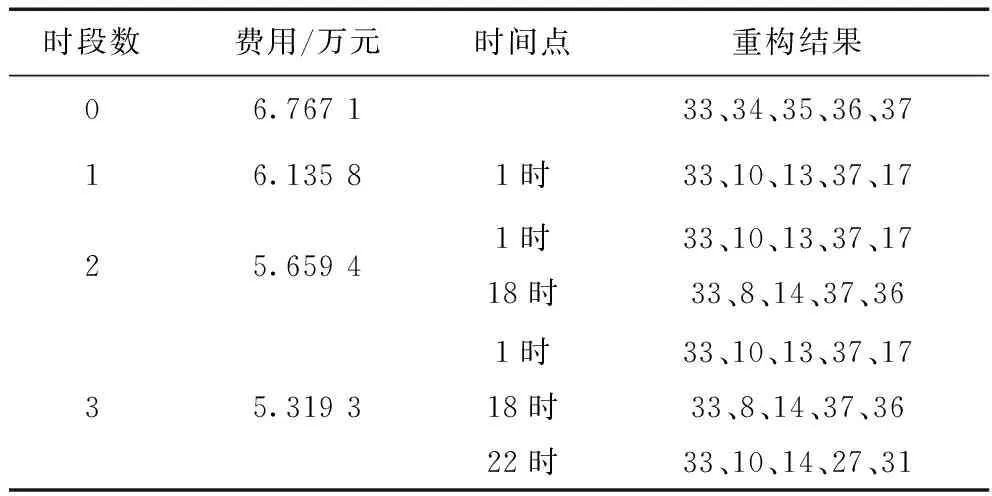
表1 改进混沌粒子群算法的优化结果

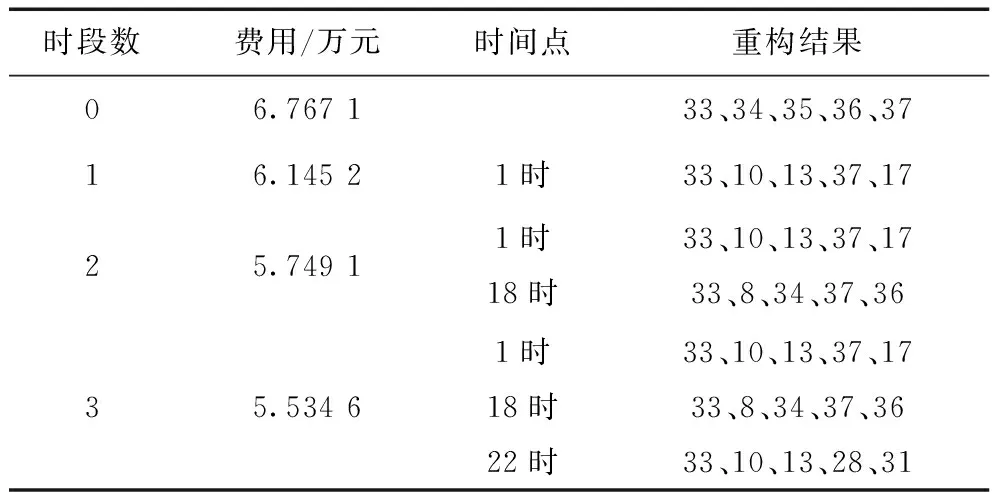
表2 粒子群算法的优化结果

另一方面，随着风光发电和电动汽车的愈加广泛的应用，考虑风光发电和电动汽车等随机负荷的配电网分时重构方案也更符合社会的需求，根据表1～表2和图7的仿真结果表明，考虑到风光发电和电动汽车的配电网重构，不仅能够实现削峰填谷的功能，同时将使得电网成本降低，提高了配电网的经济性和稳定性。

图7 加入风光电动汽车前后的总负荷曲线

5 结论

本文运用一种改进的混沌粒子群算法，在混沌粒子群算法中引入变异因子，对以配电网网损，风光电购入以及电动汽车充放电成本之和的目标函数，进行配电网分时动态重构的寻优。

针对现如今应用越来越广泛的风光发电和包含共享电动车的电动汽车等，本文根据其发电特性和分布特点分别建立模型，并利用蒙特卡罗法拟合出其负荷曲线。

本文采用所提改进混沌粒子群算法建立配电网分时重构的新模型，并将仿真的结果与粒子群算法的方案进行比较，结果表明改进混沌粒子群算法在配电网动态分时重构问题中，优化了网络结构，得到了最佳效益，具有较好的实际应用和理论指导意义。

参考文献：

[1]RAJARAM R, KUMAR K S, RAJASEKAR N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with Distributed Generation (DG)[J]. Energy Reports, 2015, 22(1):116-122.

[2]HERAZO E, QUINTERO M, CANDELO J, et al. Optimal power distribution network reconfiguration using Cuckoo Search[C]// International Conference on Electric Power and Energy Conversion Systems. IEEE, 2016:1-6.

[3]周丹, 辛江, 马志刚. 基于改进遗传算法的多目标配电网重构[J]. 电网与清洁能源, 2010, 26(10):20-24.

[4]卞栋, 卫志农, 黄向前,等. 电力市场中含分布式电源的配电网重构模型[J]. 电力系统保护与控制, 2013,41(11):117-123.

[5]赵晶晶, 李新, 彭怡,等. 基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J]. 电网技术, 2009, 33(17):162-166.

[6]张涛, 史苏怡, 徐雪琴. 基于二进制量子粒子群算法的含分布式电源配电网重构[J]. 电力系统保护与控制, 2016,44(4):22-28.

[7]吴泓俭, 雷霞, 刘斌,等. 基于遗传膜算法的含风电机组和电动汽车的配电网分时段动态重构[J]. 电工技术学报, 2016, 31(2):196-205.

[8]桂灿芝. 含光伏出力的配电网动态重构与检修优化研究[D]. 杭州：浙江大学, 2017.

[9]SAJAD N R,MOHAMMAD R J O, MASOUMEH K.Multi-objective planning model for simultaneous reconfiguration of power distribution network and allocation of renewable energy resources and capacitors with considering uncertainties[J].Journal of Central South University,2017,24(8):1837-1849.

[10]梁文举,田昊,姚凡.计及可靠性含M-V-U的配电网动态重构[J].电测与仪表,2017,54(20):76-81.

[11]王力,倪俊,吕静,等.动态粒子群算法用于负荷变化的配电网重构[J].湖北民族学院学报(自然科学版),2017,35(3):328-332.