基于海量用电数据的用户负荷模式快速提取方法研究
卢锦玲, 马 冲, 冯翠香
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
随着智能电表的普及和数量的日益增多,由大规模智能电表采集得到的用电数据不仅具有大数据的4 V特点(volume, variety, velocity and value),还具有电力系统特有的3E特点(energy, exchange and empathy)[1]。对海量用户用电数据的有效分析不仅可以满足负荷预测、风险预警、异常检测、负荷模式提取、优化生产调度、需求响应分析等[2-4]的基础工作,还可以科学地提高电网自动化水平,从而实现电网可靠、安全、经济、高效、和谐友好和用电安全的环境。
对负荷模式的有效提取对应用于负荷控制、负荷预测、风险预警、分时电价的制定与实施、用电异常检测等[5-10]具有重要的指导作用,负荷模式提取的准确性很大程度上影响后续工作的稳定进行。目前国内外对用电大数据的负荷模式提取研究,已成为当下热点课题[11-14]。文献[6]利用云计算强大的数据存储及并行计算能力,进行Map-Reduce并行处理模型下基于改进K-means算法的海量用户用电数据并行挖掘。文献[7]针对单一聚类算法的不足,研究基于经典聚类算法的集成算法,并将其应用于负荷曲线聚类,最后结合主成分分析降维方法对高维数据进行降维。文献[12]利用K-means算法具有收敛速度快、效率高的优势,采用了改进K-means算法对用户进行聚类,并根据模型对负荷需求进行预测。文献[15]提出了一种函数型聚类分析方法,利用K-means聚类算法,对海量电力用户稀疏、不规律的日耗电量数据进行特征分析,并对用户进行分类。文献[16]利用基于聚类有效性修正的德尔菲方法配置特性指标权重,提出一种特性指标降维的日负荷曲线聚类方法。但在聚类过程中,由于聚类中心点的随机选取使得聚类结果稳定性不高。文献[17]利用改进K-means聚类算法,并结合有效指标准则,能够有效地提取出日负荷曲线,但该方法需要遍历所有聚类数K,以得到最优聚类数,使得算法效率不高。
由此可以看出,国内外对海量负荷模式的提取主要集中在对算法的改进和大数据处理效率方面[8-12],其聚类可靠性高,处理大数据时有显著优势,但是对数据清理方面所做工作较少,往往使得修正后数据准确率有待提高,此外,在对用户更细粒度的聚类研究较少,当用户种类较多时提取最优负荷模式所用时间较长。
针对上述问题,本文首先考虑到用电大数据的分布特点,将四分位法与3σ法相结合,提出一种“横向—纵向”法来对异常用电数据检测与修正,以提高数据修正的速率与准确率;其次,综合对比了几种典型的数据降维方法,得出用主成分分析法对海量用电数据进行降维后将极大地提高负荷模式提取效率;最后,在传统K-means算法简单快速优势的基础上改进得到Fast K-means(FK-means)算法,该算法利用二分法思想来减小聚类时间,将聚类有效性指标DBI与CHI相结合来提高聚类结果可靠性,该算法不仅具有鲁棒性好,对负荷模式提取速率快的优势,并且随着电力用户种类的增多,效果提升更明显。
1 负荷模式提取流程
本文将从负荷模式提取的各个步骤来详细介绍,具体流程如图1所示。对负荷模式提取的步骤如下:
(1)对采集得到的用户用电数据进行异常值处理:包含离群点和空缺值,并对处理后的数据进行归一化处理。
(2)对数据进行降维处理。
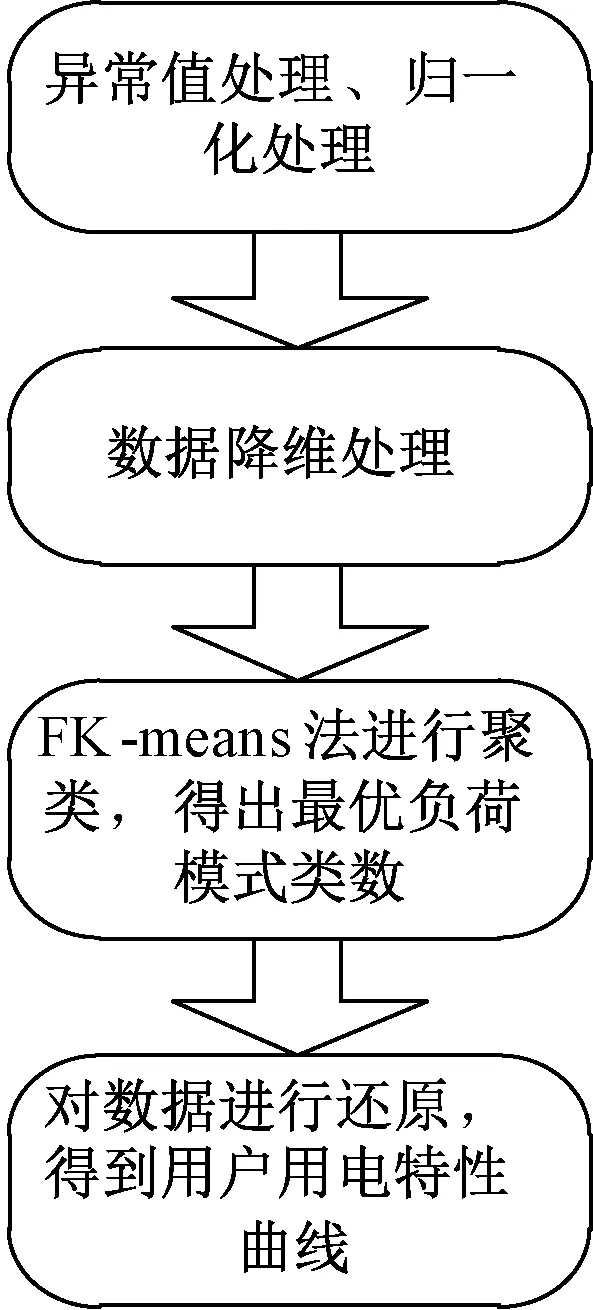
图1 FK-means算法对负荷模式提取流程图
(3)采用FK-means算法进行聚类,快速确定最优聚类数所在区间,并计算最优聚类数所在区间中DBI与CHI指标,从而得到max{CHIK-DBIK},K即为对应的最优聚类数。
(4)对数据还原,从而得到聚类后的用户用电特性曲线。
2 数据处理
2.1 数据预处理
由于用电数据在横向上具有相似性,短时间间隔内(本文处理的用电数据采集时间间隔为30 min,每个用户采集30天)在纵向上具有无突变性的特点,而且用电数据为单一属性数据。本文根据用电数据的分布和属性特点,提出一种“横向—纵向”法来辨别修正异常用电数据。
由于用电数据的横向相似性,在横向上利用四分位法简单快速的优势来对异常用电数据进行初步定位,其定义如下。
(2)其中前25%为上四分位用FL表示,后25%处于下四分位用FU表示。四分位数间距为:dF=FU-FL,上截断点为:Q1=λdF-FL,下截断点为:Q2=FU+(1-λ)dF。
(3)其中小于Q1或者大于Q2的数据将其初步定为异常用电数据。
上式参数λ取值0.5~1,本文λ取为0.85。
在横向上用四分位法对用电数据进行粗辨识后,利用短时间间隔内用电数据在纵向上无突变性的特点,对初步筛选出的异常用电数据在纵向上用3σ法的精确性对其进一步辨别并修正,其定义如下。
(1)
(2)
(3)

凡满足式(3)的均为异常用电数据,将异常用电数据用其所在时刻的其他样本点的平均值来代替。
2.2 数据归一化
对用电数据进行处理后,取各用户月数据(不含周末)平均值作为典型日负荷曲线,每条负荷曲线表示为xi={xi,j,j=1,2,…,n},由于每个负荷样本具有不同的最大最小负荷,为了后续方便分析,采用如下的方法进行数据归一化:
(4)

3 降维处理
对用电数据进行处理后得到的用户典型日负荷曲线仍具有维度高的特点,使得后续聚类耗时较长。为了对海量用户进行负荷模式提取时能够进一步提高效率,有必要对高维数据进行降维处理,降维的目的是用较低维数的向量来表示负荷曲线。降维不仅能够节约数据的存储空间,还能够减少计算时间,提高算法效率。本节对当下主流的无监督降维方法进行对比分析,从而选取一种最优降维方法。
3.1 降维方法
常用的无监督降维方法有主成分分析PCA、局部保持投影LPP、特征值提取FE[18]等。
(1)主成分分析PCA(Principal Component Analysis, PCA)
PCA的目标是通过某种线性投影,将高维的数据映射到低维的空间中表示,并期望在所投影的维度上数据的方差最大,以此使用较少的数据维度,同时保留住较多的原数据的特性。目标函数定义如下:
E(S)=STPTS
(5)

考虑到约束条件STS=1,利用拉格朗日乘子法,构造拉格朗日函数为:
L(S,φ)=STPTS-φ(STS-1)
(6)
式中:φ为拉格朗日乘子;对式(6)中S求偏导,令偏导数为零,之后便转化为求ST特征值的问题,将前d个最大的特征值组成投影矩阵,从而将高维数据通过投影矩阵映射到d维上。
(2)局部保持投影LPP(Locality Preserving Projections, LPP)
LPP是能够保护数据中的簇结构的线性降维方法。设yi为xi的一维描述,其目标函数如下:
(7)
式中:A为投影降维矩阵;相似度矩阵W=[Wij]N×N为对称阵,矩阵内部元素定义为:
(8)
式中:参数δ0等于总体样本方差;xi∈N(xj)表示xi与xj相邻。
从该方法的权值矩阵S的设置中可以看出,其在对应近邻样本的位置上赋了一个非零权值,而对于相距较远的样本则赋零。这样就可以在投影中,达到保留样本的近邻结构的目的。
(3)特征值提取FE(Feature Extraction, FE)
特征值提取法是对每条负荷曲线提取特性指标,本节采用6种特性指标,分别为:日负荷率、最高利用小时率、日峰谷差率、峰期负载率、平期负载率、谷期负载率。
3.2 降维结果分析
在原始数据保留度相同的情况下,对部分样本采用上述降维方法进行降维,对比结果如图2所示。

图2 各种降维算法计算时间
从图2可以看出,随着数据量的增加,LPP用时最多,PCA用时最少,且数据量越大越明显,故选用主成分分析PCA来对样本数据进行降维。
4 负荷模式提取
传统K-means算法具有简单、收敛速度快的优势,其时间复杂度为O(KNT),其中K为聚类数,N为样本总数,T为迭代次数。但传统K-means算法有两点不足:聚类数K与初始聚类中心需要事先确定。本节将介绍FK-means算法如何减小聚类时间并提高稳定性。
4.1 聚类有效性指标
聚类有效性是通过建立有效性指标,评价最佳聚类质量并得到最佳聚类数的过程,当数据的原始正确划分未知时,采用内部评价指标。常用的内部评价指标有DBI(Davies-Bouldin Index)指标、XBI(Xie-Beni Index)指标、CHI(Calinski-Harabasz Index)指标和PBM指标[19]。其定义分别如下。
(1)DBI指标
(9)
式中;Ci为类簇i所构成的集合;Wi表示类Ci中的所有样本到其聚类中心的平均距离;∣Cij∣表示类Ci与Cj中心之间的距离。可以看出DBI指标越小表示类与类之间的相似度越低,同一类内的相似度越高,从而对应的聚类数越佳。Wi与∣Cij∣表达如下:
(10)
式中:ni表示类Ci中样本数据xi的个数;Zi为类Ci中心点。
(11)
(2)XBI指标
(12)
式中:μij是一个布尔值。当xj属于第i类时,μij为1,否则为0。分子表示属于同一类簇的样本到其类簇中心的距离,衡量紧密性;分母表示不同类簇中心之间的距离,衡量分离性,因此XBI值越小,聚类效果越好。
(3)CHI指标
(13)
式中:类内离差WGSS定义如下:
(14)
类间离差BGSS定义如下:
(15)
式中:Z为整个样本集的中心。
该指标分母衡量类内紧密性,分子衡量类间分离性,因此CHI指标越大聚类效果越好。
(4)PBM指标
(16)
式中:DB表示样本中类簇中心间的最大距离,即:
(17)
式中:EW表示样本中每个类簇内的所有点到该簇质心的距离之和,即:
(18)
式中:ET表示样本中所有点到整个样本集中心的距离之和,即:
(19)
PBM指标越大,聚类效果越好。
4.2 聚类指标分析
本次实验数据取自SEAI发布的爱尔兰智能电表实际量测数据,采集频率为30 min,实验数据包含24 611条负荷曲线。对实验数据进行处理并聚类,聚类所得的各聚类指标与聚类数的关系如如图3所示。

图3 各聚类指标与聚类数的关系
从图3可以看出,4种聚类指标随着聚类数目的增加都有一个最大转折点,即为对应的最优聚类数。不同的是,PBM指标数值较大,而XBI指标数值较小,若作为评价指标使用则对比效果不明显,此外,若采用单一聚类指标评价聚类结果,则可靠性不高。由于CHI与DBI指标特点具有互补性,且指标数值较为接近。故本文采用CHI与DBI指标相结合的方法,以提高聚类结果的准确性和稳定性。
4.3 聚类数的确定
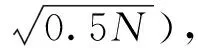

图4 FK-means聚类
根据CHI与DBI指标的特点,λ1取0.5,λ2取0.9。本文α取0.8。
4.4 聚类中心的确定
由于随机确定初始聚类中心,使得传统K-means稳定性不高。为了解决上述问题,本文采用基于“最大最小距离”法来确定初始聚类中心,即初始聚类中心相距尽可能远,避免了初始聚类中心过于临近而陷入局部最优,从而获得更高质量的聚类。“最大最小距离”法原理如下:
(1)先从总样本数据集X={x1,x2,…,xN}中随机挑选一个xi作为初始中心点A。
(2)计算余下数据集中每个样本点与初始中心点A的距离,选取距离最大的样本点作为中心点B。
(3)再计算余下数据集中每个样本点与各个中心点的距离distiA与,得到两个中心距离中最小的点min{disti,A,distiB},再从所有样本点的距离中找到最大的距离,此样本点作为下一个中心点C。迭代条件满足:
式中:distiA为样本点xi与中心点A之间的距离;distiB为样本点xi与中心点B之间的距离;distiC为样本点xi与中心点A、B距离的最小值;DistiC为样本点xi中所有最小距离中的最大值。
(4)重复步骤3,直到选取K个中心点。
以上是初始聚类中心的选取原则,在之后迭代中,聚类中心取聚类后类间距离的平均值作为新的聚类中心。当聚类中心不再发生变化时,则迭代结束算法收敛。
5 算例分析
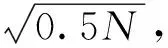


图5 用户日用电模式结果
5.1 负荷模式提取效率分析
为便于直观分析,用典型用电曲线代表所在类簇的负荷,将典型用电曲线进行类比,得到的用户日用电模式结果如图5所示。
从图中可以看出,类1、类7、类8、类9、类11、类14和类16在晚间用电量大,此类用户多为娱乐消费场所或写字楼等;类2、类4、类5午和类13午间用电量大,此类用户多为居民用电或医院学校等;类3,、类6、类10和类15用电较为平缓,但是用电量有所差异,此类用户多为商业或工业等用电,并根据用电量的大小可以划分商业或工业规模的大小;类12和类17用电波动较大,此类用户多为农业用电。
用FK-means算法对数据集聚类所用的时间为1 104.59 s。而将最大聚类数Kmax设定为80时,采用传统K-means法来进行负荷模式提取,用传统K-means算法对数据集进行聚类后所用时间为 4 634.83 s。可以看出,FK-means算法相较于传统K-means算法计算时间大幅降低,并且随着用户种类的增多,FK-means算法这一优势越明显。
用FK-means算法分别对降维前后的用电数据进行负荷模式提取,其中对降维后的负荷模式提取耗时306.37 s,而对未降维的用电数据进行聚类所需时间为1 104.59 s,可见结合降维技术的FK-means算法在对负荷模式提取时效率更高。
5.2 负荷模式提取可靠性分析
K-means算法对负荷模式进行提取时异常用电数据直接进行删除,而FK-means算法采用“横向—纵向”检测法来对异常用电数据进行修正。从37 611个用户数据中选取部分数据进行对比验证。两种情况下的聚类差异性如表1所示。

表1 FK-means算法与K-means算法聚类结果差异比较
从表1可知,FK-means算法比K-means算法聚类所得结果可靠性更高,由于K-means算法对异常用电数据直接进行删除,随着异常用电数据的增加,其对聚类产生的影响越明显,得到的结果越不可靠,此外,由于传统K-means是随机产生初始聚类中心,使得聚类结果易陷入局部最优,无法得到高质量的聚类。而FK-means算法在经过“横向—纵向”法对异常用电数据修正之后,其对整体聚类结果所产生的影响可以忽略,并且消除了初始聚类中心的随机性问题,从而使得聚类结果更稳定,算法鲁棒性好。
6 结论
本文提出了一种FK-means算法的电力用户用电特性快速提取法。
(1)本文采取一种“横向—纵向”检测法,来检测并纠正异常用电数据,首先利用四分位法简单快速的优势,初步确定异常用电数据点,然后利用3σ法的精确性,对初步确定的异常用电数据进一步检测并修正。
(2)对于海量的高维负荷曲线,本文对比了几种常用的降维方法,从而得出主成分分析法用时最短,效率最高。
(3)为了降低负荷模式提取所用时间,本文利用二分法思想来快速确定最优聚类数范围,极大地减小了聚类时间。为了提高负荷模式提取结果的可靠性,本文对比了几种常用的聚类有效性指标,采用DBI与CHI指标相结合的方法,两种指标相结合使得聚类结果更稳定更准确。
(4)本文提出的FK-means算法能够快速准确的确定最优聚类数,相较于传统的K-means算法,FK-means算法能够显著减小聚类时间,鲁棒性好,并且对处理大数据具有很大优势。
参考文献:
[1]DEFU C. Electric power big data and its applications[A]. Science and Engineering Research Center. Proceedings of 2016 International Conference on Energy, Power and Electrical Engineering (EPEE2016)[C]. Science and Engineering Research Center, 2016: 4.
[2]王桂兰, 周国亮, 赵洪山, 等. 大规模用电数据流的快速聚类和异常检测技术[J]. 电力系统自动化, 2016, 40 (24): 27-33.
[3]宋亚奇, 周国亮, 朱永利. 智能电网大数据处理技术现状与挑战[J]. 电网技术, 2013, 37 (4): 927-935.
[4]张素香, 赵丙镇, 王风雨, 等. 海量数据下的电力负荷短期预测[J]. 中国电机工程学报, 2015, 35 (1): 37-42.
[5]冯丽, 邱家驹. 基于电力负荷模式分类的短期电力负荷预测[J]. 电网技术, 2005 (4): 23-26.
[6]赵莉, 候兴哲, 胡君, 等. 基于改进k-means算法的海量智能用电数据分析[J]. 电网技术, 2014, 38 (10): 2715-2720.
[7]张斌, 庄池杰, 胡军, 等. 结合降维技术的电力负荷曲线集成聚类算法[J]. 中国电机工程学报, 2015, 35 (15): 3741-3749.
[8]王德文, 周昉昉. 基于无监督极限学习机的用电负荷模式提取[J/OL]. 电网技术, 1-8[2017-12-24].https://doi.org/10.13335/j.1000-3673.pst.2017.1644.
[9]赵岩, 李磊, 刘俊勇, 等. 上海电网需求侧负荷模式的组合识别模型[J]. 电网技术, 2010, 34 (1): 145-151.
[10]陆俊, 朱炎平, 彭文昊, 等. 智能用电用户行为分析特征优选策略[J]. 电力系统自动化, 2017, 41 (5): 58-63.
[11]冯晓蒲, 张铁峰. 基于实际负荷曲线的电力用户分类技术研究[J]. 电力科学与工程, 2010, 26 (9): 18-22.
[12]VIEGAS J L, VIEIRA S M, SOUSA J M C. Electricity demand profile prediction based on household characteristics [C]//European Energy Market. IEEE,2015:1-5.
[13]张素香, 刘建明, 赵丙镇, 等. 基于云计算的居民用电行为分析模型研究[J]. 电网技术, 2013, 37 (6): 1542-1546.
[14]朱文俊, 王毅, 罗敏, 等. 面向海量用户用电特性感知的分布式聚类算法[J]. 电力系统自动化, 2016, 40 (12): 21-27.
[15]张欣, 高卫国, 苏运. 基于函数型数据分析和k-means算法的电力用户分类(英文)[J]. 电网技术, 2015, 39 (11): 3153-3162.
[16]刘思, 李林芝, 吴浩, 等. 基于特性指标降维的日负荷曲线聚类分析[J]. 电网技术, 2016, 40 (3): 797-803.
[17]刘莉, 王刚, 翟登辉. k-means聚类算法在负荷曲线分类中的应用[J]. 电力系统保护与控制, 2011, 39 (23): 65-68.
[18]谭璐. 高维数据的降维理论及应用[D]. 北京:国防科学技术大学, 2005.
[19]谢娟英. 无监督学习方法及其应用[M]. 北京:电子工业出版社, 2016.

