融资融券对股市波动的影响研究——以沪深市场为例

(天津财经大学 天津 300222)

一、数据来源和处理

本文选择2016年5月3日到2017年11月28日共385个观察数据，数据来自于东方财富网站。本文采取沪深两市的融资余额总量X1代表指标融资余额，并取对数来消除异方差形成新变量lnX1；融券余额用沪深两市的融券余额总量表示指标融券余额，用X2表示并取对数来消除异方差形成新变量lnX2；股市波动性采用沪深300指数的日波动率来表示，第t日的价格波动率计算公式如下：Yt=(Ph-Pl)/[(Ph+Pl)/2]，其中Pl代表当天的最低价格，Ph代表当天的最高价格。

二、实证分析

(一)检验变量平稳性

因为经济类数据很大程度上是非平稳，所以在建立向量自回归模型之前需要检验各个序列是否平稳，在这里采用ADF单位根检验，结果如下：

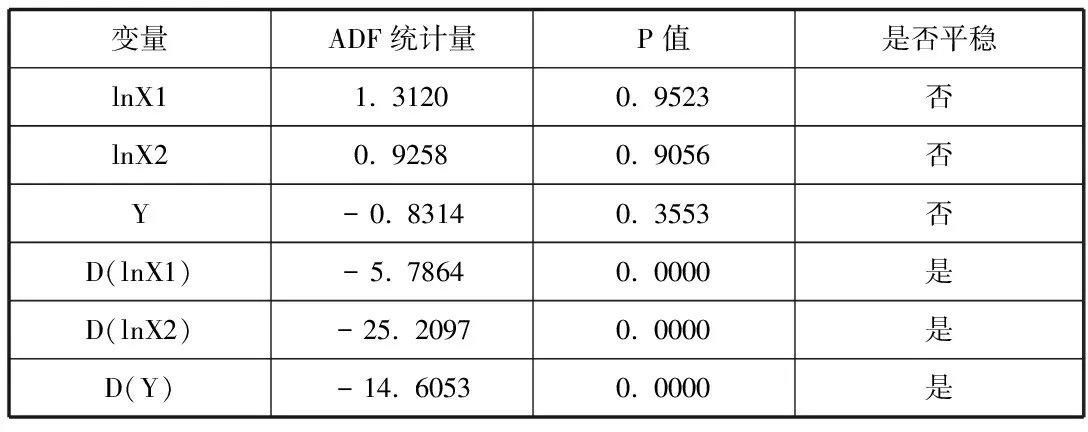
表1 ADF单位根检验表

上述结果显示变量lnX1，lnX2，Y的ADF检验对应的p值分别为0.9523，0.9056，0.3553，均大于0.05，故可认为三个变量在ADF单位根检验下均为非平稳状态。接下来对lnX1，lnX2，Y序列分别作一阶差分形成新序列D(lnX1)，D(lnX2)，D(Y)，再分别对其作ADF单位根检验，新变量D(lnX1)，D(lnX2)，D(Y)相对应的p值都为0.0000，均小于0.05，表示各变量一阶差分后在5%置信水平下均为平稳状态。故变量lnX1，lnX2，Y均为一阶单整序列。

(二)VAR模型滞后阶数选择

一般来说，滞后期的确定常用以下两种方法：一是根据经济理论确定；二是由AIC和SC值得到。一般人们用AIC或SC准则来确定最合适滞后期。首先初步建立向量自回归模型，然后在生成的界面下通过选择lag length criteria,不断对滞后阶数进行调整并观察AIC值和SC值的大小，最终发现当滞后期为3时，AIC和SC值分别为-19.98和-19.67，在所有滞后期的AIC和SC值中为最小，由AIC和SC同时最小规则知，滞后阶数应选择3。

(三)协整检验

上文发现原始变量经过一阶差分后才平稳，原序列可能存在“伪回归”导致方程不准确的状况，所以在此采用Johnson检验法检验各序列间是否存在协整关系，当原假设为0个协整向量*时，其相应的特征值、最大特征值统计、5%统计临界值和P值分别为0.1745、72.8765、21.1316和0.0000；当原假设为至多1个协整向量时，其相应的特征值、最大特征值统计、5%统计临界值和P值分别为0.0234、8.9982、14.2644和0.2863；当原假设为至多2个协整向量时，其相应的特征值、最大特征值统计、5%统计临界值和P值分别为0.0027、1.0407、3.8414和0.3077。第一个检验的统计量的p=0.00<0.05,表示拒绝有0个协整向量的原假设；第二个检验的统计量p=0.2863>0.05，表示接受至多有1个协整向量的原假设，所以综合来看，序列间有一个协整关系，因此可建立ECM模型。

(四)误差修正模型

在上述基础上，建立协整方程研究融资融券余额与股市波动的长期关系。

Y=-0.0074lnX1-0.0009lnX1+0.0759

(1)

从(1)来看，在长期内，融资余额每增加1%，股市波动率平均减少0.0074%；融券余额每增加1%，股市波动率平均减少0.009%。总的来数，融资余额、融券余额都能在一定程度上减少股市波动，但融资余额对抑制股市波动的作用更大。

通过协整分析发现融资余额、融券余额与股市波动率间有长期稳定的关系，为了更深一步研究它们在短期内的动态变化关系，需要建立误差修正模型。

D(Y)=-0.9141ecm(-1)-0.2290*D(lnX1(-1))+0.0124*D(lnNX1(-2))+0.0196*D(lnX2(-1))+0.0232*D(lnX2(-2))-0.0891*D(Y(-1))-0.0178*D(Y(-2))+3.55e-05

(2)

从(2)来看，在短期内，融资余额每增加1%，股市波动率平均减少0.229%；融券余额每增加1%，股市波动率平均增加0.0196%。误差修正系数-0.9141说明当股市的波动偏离均衡时，整体会以0.9141的速度反向逐步调整至均衡水平。

(五)格兰杰因果检验

本部分利用格兰杰因果检验来探究融资余额、融券余额对股市波动率有没有因果关系，检验的两个假设分别是：

原假设 H0：被检验的解释变量和因变量没有Granger因果关系

备则假设H1：被检验的解释变量和因变量有Granger因果关系

接下来，我们对各变量之间进行检验。

当原假设为融资余额不是股市波动的格兰杰因果关系时，其p值为0.0015；当原假设为股市波动不是融资余额的格兰杰因果关系时，其p值为0.0240；p值分别与置信水平0.05相比可得，融资余额(lnX1)构成对股市波动(Y)的格兰杰因果关系；反之，股市波动也构成对融资余额的格兰杰因果关系。当原假设为融券余额不是股市波动的格兰杰因果关系时，其p值为0.0001；当原假设为股市波动不是融券余额的格兰杰因果关系时，其p值为0.0062；p值分别与置信水平0.05相比可得，融资余额(lnX1)构成对股市波动率(Y)的格兰杰因果关系；反之，股市波动率也构成对融券余额的格兰杰因果关系。

(六)方差分解

方差分解的用途是把某一变量的浮动方差分配到各干扰项上。因此为了弄清各个解释变量对因变量的解释程度，我们接着通过Eviews8.0对股市波动Y序列进行方差分解来研究各个变量对其的贡献程度。

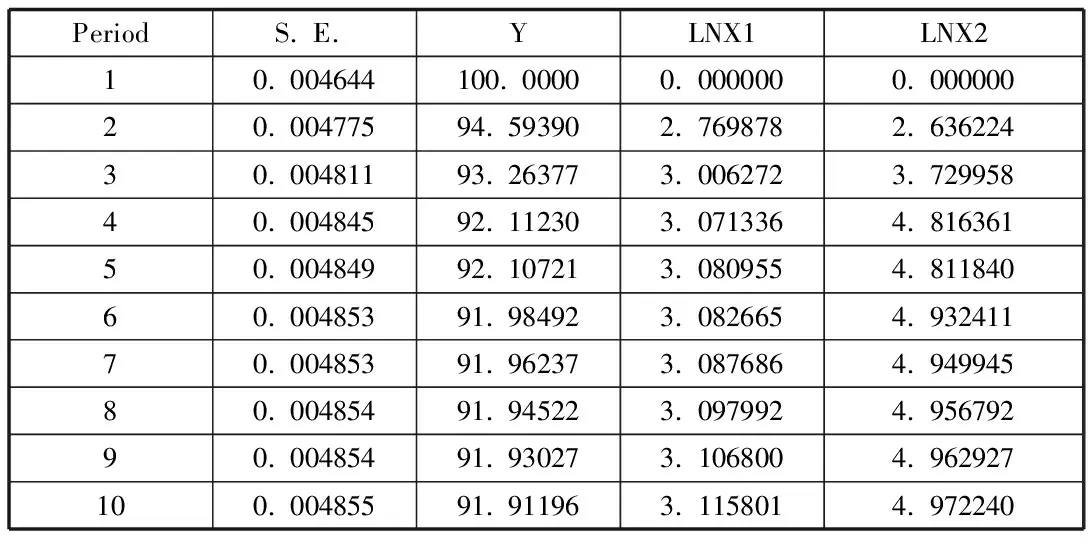
表2 股市波动的方差分解表

从表可知，从第一期到第十期，Y序列的方差变动可由自身解释部分从占100%到91.91%，呈逐渐下降趋势；lnX1序列对Y序列的方差贡献度从刚开始的2.76%到3.11%，呈逐渐上升趋势；lnX2序列对Y序列的方差贡献度从2.63%上升到4.97%。综合可知，滞后前几期内融资余额对股市波动率的方差贡献度大于融券余额，但当滞后阶数变大时，融券余额对股市波动的贡献也增强。同时也表明股市的波动性能够被其自己解释的比例较高，但是全体变量视角下，融资和融券所占的解释比重随着滞后期数的增加也越来越大。

三、结论与建议

两融业务在我国发展了多年，无论是证券市场的制度建设还是融资融券的交易规模都与日俱增。本文通过研究我国股市的两融业务现状，利用格兰杰因果检验、误差修正模型等得到一些结论。

首先，格兰杰因果关系检验显示，融资余额与股市波动互为因果关系，融券余额与股市波动彼此之间也互为因果关系。其次，由误差修正模型可得，短期时间内，增发融券业务会稍微促进股票市场的波动，融资余额的增加会抑制股市波动，但从长期影响看，融资余额和融券余额的增加都会在一定程度抑制股市波动。

最后，方差分解显示随着滞后阶数增加，融资融券余额对股市波动率影响都逐渐增加，但对股市波动方差的贡献度不是很大，从整体来看，股市波动主要受自身前期影响。说明融资融券对股市波动的影响存在时滞性。

在得出以上结论的同时，为了使股市更加稳定相应的提出一些建议：

第一，目前我国股市融资融券标的规模不是很大，可以在可控范围内扩大两融标的范围。前文分析得出两融业务能在一定程度能较少股市波动，起到稳定市场情绪作用，而且目前国内融资融券标的占据全部股票市场比例不是很大，所以在风险可控前提下，应适当扩充融资融券标的。

第二，在两融业务中，融资业务规模以及占比甚高，相反融券业务的规模和占比很小，两融业务的结构不平衡也在助推市场的不稳定，因此在扩大两融业务的前提下进一步加大融券标的的扩充。同时，建议在保证金融安全下适当的放宽两融业务的进入门槛，因为高门槛会导致部分投资者不能参与其中，打击投资者的参与情绪。

第三，注意控制融资融券的杠杆率，使杠杆率在适当范围内调整，以防止产生由于投机行为导致的杠杆率偏高的现象，同时应对配资行为进行严格监督和管理，防止因股市价格的大幅波动而造成金融性风险的发生。另外要有效监管大的投资机构与上市公司，防止出现私下联合随意调整股票价格的行为，因为一旦大机构对股价产生影响，小型投资者会形成羊群效应加剧股市的波动。

【参考文献】

[1]王富宣.证券信用交易与股市波动性[M].大连理工大学.2008(12).

[2]崔媛媛等.融资融券运行现状分析及问题研究[N].证券市场导刊.2011(8)

[3]彭泽铧.融资融券对股票市场波动性的影响.时代金融.2015年第1期

[4]高铁梅.计量经济分析方法与建模.清华大学出版社.2006年.

[5]Xiao X.Influence of Chinese Securities Margin Trading Mechanism to Stock Market Volatility[J].Advances in Asian Social Science.2012.3:589-595.