数学建模思想融入高职数学教学的探讨

陈　飞

(商丘职业技术学院，河南 商丘 476100)

0　引言

在当前社会经济与科学技术的不断发展背景下，数学已经成为了各个领域中不可或缺的一部分，并且在高职教育中，数学是一门重要的公共基础课，可以有效提高学生的基本素养.当然，从基本属性分析，高职教育的目的是培养高级技术应用型人才，所以在人才培养方面需要具备实践性、主动性以及个性化，积极将数学建模思想融入高职数学教学中，意义重大，值得研究与分析.

1　数学建模思想在高职数学教学中的重要性

在新时期，高职数学课程教学需要结合实际发展情况，将数学的应用性加以展现，其中要从根本上解决实际问题，则离不开数学建模.从理论上分析，所谓的数学建模主要是指应用数学思想与方法解决实际问题，且将显示世界的特定对象提出特定目标，并进行简化与假设，利用数学工具创建数学结构，实现优化决策[1]12-14.其中数学建模的过程见图1：

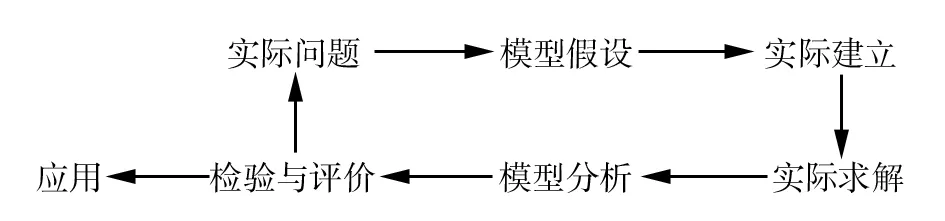
图1　数学建模的过程

1.1　符合学生的认知发展规律

一般而言，在数学建模中学生需要对问题加以观察、分析以及归纳，并及时转化为数学问题并与实际问题相互关联，完成数学建模，其流程包括了直觉——探试——出错——思考——猜想——验证，这不仅符合学生的认知条件与规律，且可在潜移默化中激发学生树立正确的学习意识，提高积极性，发挥创造性.

1.2　改变高职数学的价值取向

在当前相关政策的指引下，我国高职教育得到了快速发展，但是从整体上分析，大多数学校仍旧采取本科院校高数的教学方法，并将教学背景重点放置在理论学习以及知识掌握方面，这与高职数学教学目标背道而驰.尤其在近几年经济不断发展背景下，社会需要大量的应用型人才，积极创新教学思想、教学内容、教学方法、教学手段成为了主流意识，而将数学建模思想应用其中，便可以进一步改变数学教育的价值取向，甚至还可提高学生的数学素养.

1.3　激发学生的探索兴趣

毋庸置疑，兴趣是最好的老师，只有让学生主动参与才能提高教学质量与效率，在高职数学教学中，往往是从一个新概念、新公式出发，可以有效激发学生的主观能动性，提高其内容的应用性，并且在每一章节结束的时候，要将本章内容相关联的知识加以结合，进而激发学生的学习兴趣，让学生能够清楚地认识到数学本身便是对现实世界刻画的一个过程，并非仅仅通过理论加以推导.

2　高职数学教学中数学建模思想的应用对策

在当前职业教育发展的背景下，培养拥有多种实用技能人才是高职教育的培养目标，而数学建模，则可以解决许多实际问题.因此，要结合高职教育的特点，结合教学实际，分析高职数学教学的重要性，实现理论与实践的相互结合，完成知识传授与能力培养的整合，及时将数学建模思想融入高职数学教学中，让每一位高职学生都能够树立正确的数学意识以及数学能力.

2.1　数学建模融入到教材之中

2.1.1教材中选择合适的案例

从严格意义上探析，数学来源于现实，是现实中不容忽视的内容，作为教学的主要组织者与引导者，数学教师需要多元化的将建模思想融入其中，其中最为主要的便是要选择好载体，在进行数学总体设计的时候，严格按照课程目标以及章节内容，精选案例，或者将当前社会中具有新颖性，备受关注的热点问题融入其中，实现与课堂的相匹配.其中需注意的一点是在案例选择的时候，不可过于复杂，保证难度适中，还要指引学生对身边的事物加以留意，能够从数学的角度分析问题，最终形成案例.比如学习数学中纳税问题的时候，涉及到了诸多计算内容，包括打的计费、房贷复利计算等等，或者对于导数应用中的优化问题，怎样设置易拉罐，节省制作材料等等，将这一系列的案例融入其中，可以有效激发学生的求知欲望，并且能够在无形中教会学生怎样构建数学模型，解决数学问题[2]185-187.

2.1.2实现教材内容的优化重组

数学建模是通过多种方式解决数学问题，且建模思想是以隐性形式存在的，所以要想化隐性为显性，则需要从最初的问题出发，要对当前高职人才培养模式加以研究，把握人才培养的目标，并结合高职数学教材以及教学要求，分析学生的学习特征，对教学内容进行优化与重组.必要的时候要融入优秀的案例，渗透到数学建模思想之中，起到良好的教学效果.在数学教学中最为主要的内容便是微积分，且大多数微积分内容均是从现实生活中抽象出来的，因此该类内容自身便蕴含了丰富的数学建模思想，数学教师在讲解的时候，需要创设问题情景，揭示概念的形成，这样才能保证抽象的知识不再难懂.以极限的概念为例，在进行概念分析之前，数学教师需要先设置问题，询问学生怎样计算圆周长，然后将刘徽割圆术的案例引入，应用多媒体技术进行动画演示，让学生仔细观察，发现其中的规律，由此可得出结论：圆内接正多边形的边数越多，那么周长则越接近圆周长.通过这种方式可以让学生对极限思想有所了解，为日后学习其他内容奠定基础.或者在学习微分方程的时候，如果学生所学专业为机械专业，可以将机械专业中的钢锭锻打融入其中，如果是电力专业的学生，则可以将RLC电路问题融入，这样实现内容的优化与重组，让学生亲身体验到数学的重要性以及简单化.

2.2　教学过程中融入数学建模思想

2.2.1引入数学建模问题

数学教师不仅要让学生对数学的作用加以分析，并且要积极鼓励学生利用数学解决实际问题，其中在培养学生创新能力方面，数学建模是最为主要的载体，可以有效提高学生的洞察能力以及创造能力，甚至有学者研究表明，数学建模现如今受到了学生的关注与追捧，主要的原因是数学建模将传统模式下的数学教学思想打破，能够为数学与外界环境的关联打开通道.为从根本上将数学建模的作用充分发挥出来，笔者认为可以积极增加数学建模问题，或采取额外加分的方式进行鼓励，不仅要在平常的作业中留下数学知识题目，还要增加各类实际应用题，这种方法不仅对学生应用数学解决实际问题有所帮助，也可以提高学生的逻辑思维能力，在潜移默化中调动学生的探索精神与创造力[3]186-187.

2.2.2拓展数学教学方法

高等数学是逻辑性、抽象性很强的学科,在高职数学的教学中,要针对高职学生的特点来设置教学方法.在教学过程中，对于公式、定理等概念，要善于使用生活中的实际问题作为引例，把实际问题与理论概念联系到一起进行讲解，增强学生学习的兴趣，使枯燥的理论讲解变得生动起来.发挥Matlab,Mathematica等专业数学软件的作用,把数学建模和数学软件融入教学之中，通过软件构筑图像和模型，使教学内容更加的直观，使书本内容更加的形象化、生动化[4]22-23.

2.2.3做好强化指导

要想真正实现数学建模思想的有效应用，则需要让学生在学习数学的过程中掌握数学建模的基本方法，并且能够针对实际的情况做到学以致用.一般而言，在每学完一章节之后，数学教师要布置预期配套的建模问题，这样不仅可以提高学生的学习兴趣，并且也能够提高其分析能力.此外还要实现其步骤化，第一是准备阶段，数学教师需要提前将案例下发给学生，并且提出多个问题，让学生进行分析与思考；第二是分组阶段，数学教师要采取均衡性原则进行分组，并且小组成员要合理设置岗位，比如有的成员负责资料收集，有的负责问题讨论，有的负责模型构建，有的负责汇报发言；第三是汇报阶段，小组内推荐一名成员进行汇报，将关键点加以阐述，并且其他小组要进行提问；第四是评价阶段，数学教师需要对各个小组的汇报情况进行评价，并且根据其重点与难点进行指导.这种方式下可以提高学生的自主学习能力以及团队协作能力，当然对于对数学建模特别感兴趣的学生，还可以通过开展第二课堂的方式进行补充教学，比如采取数学建模社团、专题讲座等方式，从而提高学生的数学建模水平以及意识[5]73-74.

2.2.4培养学生数学应用能力

高职教育是为了培养应用型人才，而通过数学建模能力的培养，能够促进学生解决实际问题能力的提升.在课堂教学中，由于有固定的教学任务，想要更好地培养学生数学建模能力，必须多利用课外时间，通过开展数学建模实践活动、通过组织数学建模兴趣团体、开展集体讨论活动等形式，用实际问题作为讨论的切入点，让学生体验到从复杂的实际问题中抓住主要因素，培养解决问题的实践能力.通过实践活动的开展，可以提高学生发现问题本质的洞察力和敏锐性,从而增强数学知识与实际问题之间的转换能力,对促进学生数学应用能力的提高有重要意义[6]281-282.

总而言之，作为人才的培育者，数学教师要想将建模思想融到教学中需要从现实出发加以分析，首先要对专业课程进行系统学习，分析高职数学知识与数学建模的关系，并且增强数学建模水平.其次是要不断更新自身的知识储备能力，实现自身数学知识与专业知识的相互结合，提升自身综合能力，满足高职教育的要求.

3　结语

积极在数学教学中融入数学建模思想意义重大，可有效提高学生应用数学的能力，并且可提升学生解决数学问题的水平，在高职数学教学中，需要重视数学建模思想，认识到重要性，并且对数学知识加以观察与分析，真正提高高职数学教学的质量，满足高职数学课程教学的要求.