基于累积矩生成函数多元响应降维子空间估计*

吴 蕾，甘胜进

(福建师范大学福清分校电子与信息工程学院，福建 福清 350300)

1 问题的提出

大数据时代，数据的维数越来越高.在高维空间中进行统计建模通常会遭遇“维数祸根”问题，解决的办法之一是有效地降低变量维数，一旦维数降下来，便可利用低维上的方法处理数据.

近年来，“充分降维”因具有无模型降维的特点，引起统计学界的重视，先后产生了切片逆回归[1]、最小二乘估计[2]、海塞主方向[3]、切片平均方差估计[4]、方向回归[5]等一系列经典方法.“充分降维”的基本表述为:若存在p×k(k≤p)矩阵η，使得Y‖X|ηTX，则FY|X(y|x)=FY|ηTX(y|ηTx)，其中Y为一维响应变量，X为p维解释变量，‖表示统计独立.如此一来，Y对X条件分布不再依赖于p维的X，而是k维的ηTx，如果k相对于p充分小，那么降维的目的就达到了.称η列向量张成的子空间是一充分降维子空间.由于Y‖X|ηTX⟺Y‖X|(ηB)TX,其中B为k阶可逆方阵，因此为了保证η的可识别性，采用Y‖X|PηX，其中η列向量构成投影阵Pη(Pη=η(ηTη)-1ηT).事实上，满足上述条件的η总是存在的，如η=Ip.若所有充分降维子空间的交集仍然是充分降维子空间，则称之为中心降维子空间，记为SY|X,rank(SY|X)称为结构维数.显然，SY|X是结构维数最小的充分降维子空间.如果感兴趣的是E(Y|X)，结合“充分降维”概念，就产生了中心均值降维子空间定义，可参看文献[2]，在此不再赘述.令Z=Σ-1/2(X-E(X)),则SY|X=Σ-1/2SY|Z[6],其中Σ=D(X)>O.下文不妨假设E(X)=0，D(X)=Ip，估计降维子空间通常用到的2个基本条件为：

(1)线性条件均值.E(X|ηTX)为ηTX线性函数，即E(X|ηTX)=PηX,∀η∈Rp.

(2)常数条件方差.Var(X|ηTX)为非随机矩阵，即Var(X|ηTX)=I-Pη.

满足线性条件均值一般是椭圆分布，满足常数条件方差是多元正态分布.如果将响应变量Y推广到多维，那么就是多维响应降维子空间.朱利平等[7]基于二切片逆回归提出了累积切片估计.笔者将累积切片思想应用到矩生成函数(GF)估计[8-9],提出累积矩生成函数(CUGF)估计.

2 累积矩生成函数估计理论

记φ(t)=E(etTYX),t∈Rq，φ(t)张成的线性子空间记为M，即M=span{φ(t),t∈Rq}，则M=span{E(φ(T)φT(T))}，T是一支撑为Rq且与(X,Y)相互独立的q维随机向量.在线性条件均值下M⊆span{η}，称M为多元响应降维子空间的GF估计.结合累积切片思想，设m(y)=E(eI(Y≤y)X),MCUGF=E(m(Y)mT(Y)),其中I为示性函数，y=(y1,y2,…,yq)∈Rq，则称MCUGF为多元响应降维子空间的CUGF估计.

定理1在线性条件均值下，MCUGF=E(m(Y)mT(Y))⊆span{η}.

证明由于Y|X与Y|ηTX同分布，因此eI(Y≤y)|X与eI(Y≤y)|ηTX同分布.再结合线性条件均值和条件期望平滑性性质，可得

m(y)=E(eI(Y≤y)X)=E(E(eI(Y≤y)|X)X)=E(E(eI(Y≤y)|ηTX)X)=

E(E(eI(Y≤y)|ηTX)E(X|ηTX))=PηE(eI(Y≤y)X)⊆span{η}.

证毕.

3 模拟实验

表1示出100次重复下，CUGF估计与g-CUGF估计性能比较结果.

表1 CUGF估计与g-CUGF估计在不同样本容量和维数时的模拟性能比较Table 1 Performace of CUGF Estimation Compared with g-CUGF Estimation with Different Sample Sizes and Dimensions

续表1Continued

图1，2示出样本容量n=600，维数p分别为10和20时，g-CUGF，CUGF和GF估计在模型1下100次蒙特卡罗模拟的箱线图.

图1 当n=600,p=10时3种估计的效果Fig.1 Boxplot of Three Methods for n=600,p=10

图2 当n=600,p=20时3种估计的效果Fig.2 Boxplot of Three Methods for n=600,p=20

从图1，2可看出，g-CUGF估计的表现最优，相比于GF估计，CUGF估计的表现也不错.

Y对X回归函数既有线性关系，又有非线性关系.图3，4示出样本容量n=600，维数p分别为10和20时，g-CUGF,CUGF和GF估计在模型2下100次蒙特卡罗模拟的箱线图.

图3 当n=600,p=10时3种估计的效果Fig.3 Boxplot of Three Methods for n=600,p=10

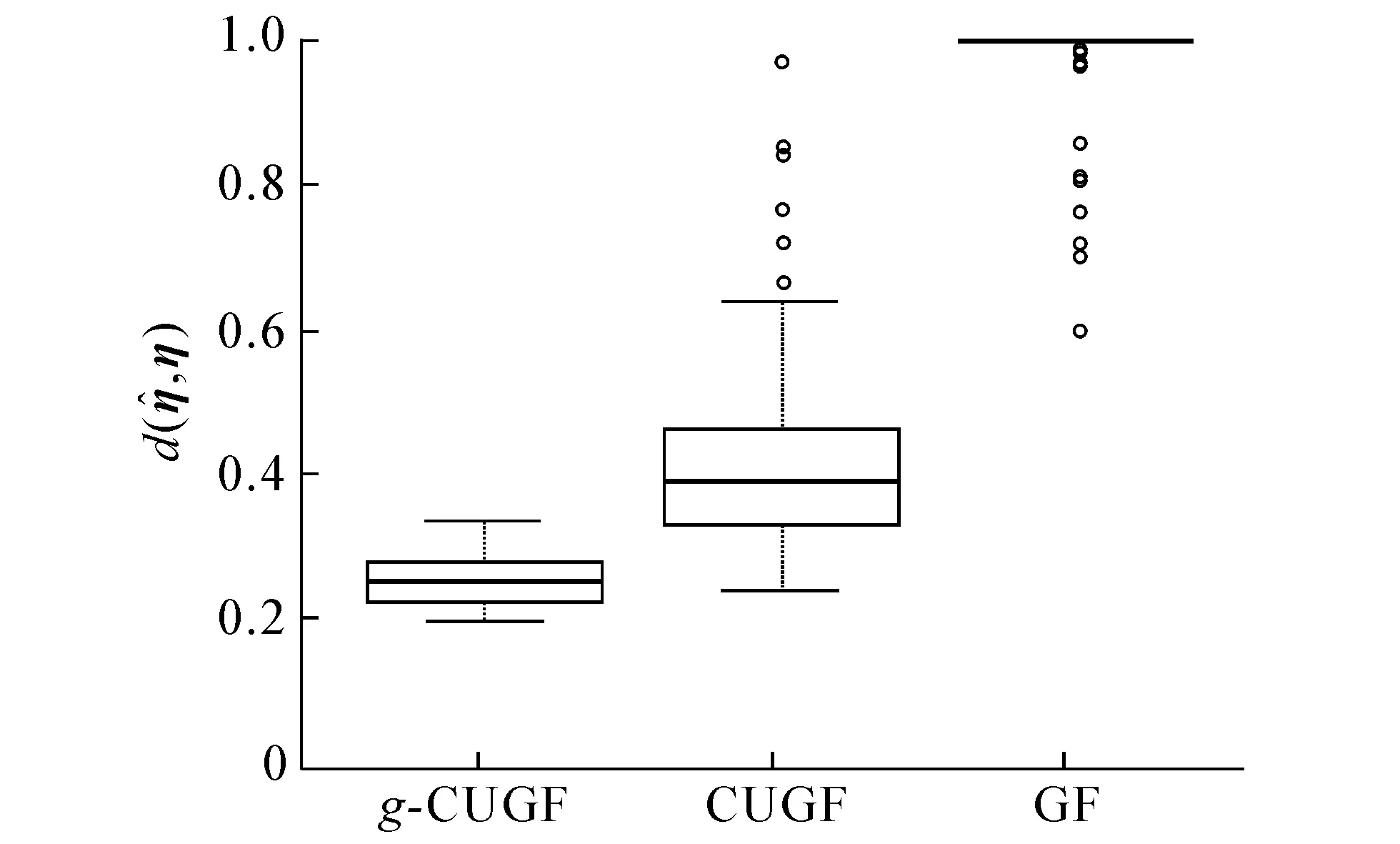
图4 当n=600,p=20时3种估计的效果Fig.4 Boxplot of Three Methods for n=600,p=20

从图3，4可看出，GF估计的表现相比其他2种估计相差甚远，而g-CUGF估计的表现明显优于CUGF估计.

4 结语

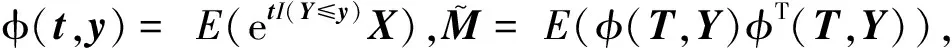
参考文献：

[1] LI KER-CHAU.Sliced Inverse Regression for Dimension Reduction[J].Journal of the American Statistical Association,1991,86(414):316-327.

[2] COOK R DENNIS,LI Bing.Dimension Reduction for Conditional Mean in Regression[J].Annals of Statistics,2002,30(2):455-474.

[3] LI KER-CHAU.On Principal Hessian Directions for Data Visualization and Dimension Reduction:Another Application of Stein's Lemma[J].Journal of the American Statistical Association,1992,87(420):1 025-1 039.

[4] BRILLINGER DAVID R.Sliced Inverse Regression for Dimension Reduction:Comment [J].Journal of the American Statistical Association,1991,86(414):328-332.

[5] LI Bing,WANG Shaoli.On Directional Regression for Dimension Reduction[J].Journal of the American Statistical Association,2009,102(479):997-1 008.

[6] COOK R DENNIS.Regression Graphics:Ideas for Studying Regressions Through Graphics[M].New York:Wiley,1998：103-105.

[7] ZHU Liping,ZHU Lixing,FENG Zhenghui.H.Dimension Reduction in Regressions Through Cumulative Slicing Estimation[J].Journal of the American Statistical Association,2010,105(492):1 455-1 466.

[8] 甘胜进,游文杰.基于矩生成函数的多元响应降维子空间估计[J].东北师大学报(自然科学版),2017,49(1):43-47.

[9] 甘胜进,涂开仁,游文杰.一类多元响应降维子空间的估计及其应用[J].统计与信息论坛,2017,32(10):18-23.

[10] FENG Zhenghui,WEN XUERONG MEGGIE,YU Zhou,et al.On Partial Sufficient Dimension Reduction with Applications to Partially Linear Multi-Index Models[J].Journal of the American Statistical Association 2013,108(501):237-246.

[11] LI Bing,ZHA Hongyuan,CHIAROMONTE FRANCESCA.Contour Regression:A General Approach to Dimension Reduction[J].Annals of Statistics,2005,33(4):1 580-1 616.