分数阶Bao混沌系统的同步控制及加密仿真*

雷腾飞，付海燕，臧红岩，苏 敏

(齐鲁理工学院电气信息工程学院,山东 济南 250200)

300多年前，整数阶微积分被提出不久便出现了分数阶微积分，因此两者具有同样长的历史，但后者因其物理意义不明确而发展缓慢[1].近几十年来，随着非线性动力学理论的发展与完善，分数阶非线性系统及分数阶控制系统成为新的研究热点，学者们提出了许多分数混沌系统，如分数阶Chen系统[3-4]、分数阶Lü系统[5]和分数阶Lorenz系统[6-9]等.目前，在分数阶混沌系统方面已经取得了一定的研究成果，研究方法主要包括频域法[9-10]、预估-矫正法[4]和Adomian分解法[11]，其中Adomian分解法因效果良好而备受关注.贺少波等[11]对一类简化Lorenz系统进行了CO与SE复杂度、分岔图等动力学分析.分数阶同步方法主要包括投影同步[12]、单向耦合同步[13]、自适应控制同步[14]和主动控制同步[15]等.这些同步方法为分数阶混沌系统在保密通信方面的应用提供了坚实的理论基础，并有效地促进了其在图像及视频加密等领域中的应用.鉴于此，笔者拟对分数阶Bao混沌系统的非线性项进行分解，从而得出系统的混沌吸引子，并在此基础上设计分数阶混沌系统的同步控制器和分数阶混沌保密通信系统.

1 分数阶Bao混沌系统

1.1 Adomian分解法及吸引子

包伯成等[7]提出了一种新的混沌系统，即满足条件a12a21=0的过渡混沌系统.笔者在此基础上提出分数阶混沌系统，其动力学方程为

(1)

其中：x(t),y(t),z(t)为系统变量；a,b,c为系统系数.给定初始状态

根据Adomian分解法和分数阶微积分性质给对应的变量赋值，令

(2)

根据Adomian分解法进行运算可得：

(3)

(4)

(5)

(6)

(7)

根据方程组(1)—(7)可求得系统方程的解为

当a=20,b=4,c=32，q1=q2=q3=q=0.9时，运用Matlab软件对Adomain分解下的Bao系统进行数值仿真，得到系统(1)的混沌轨迹即系统的吸引子，如图1所示.

图1 系统吸引子Fig.1 System Attractor

1.2 参数a的变化

固定参数b=4,c=32,改变参数a(a∈[10,30])，当q1=q2=q3=0.9时，系统(1)关于x的分岔如图2a所示.从图2a可以看出：系统由倒置倍周期脱离混沌状态，且都存在周期窗口，但周期窗口的区域不同；当a∈[25.5,30]与a处于12附近时，系统处于周期运动.

为了进一步分析系统的复杂度，当q1=q2=q3=0.9时，Lyapunov指数谱随着a的变化而变化的情况如图2b所示.从图2b可以看出：在周期态最大，Lyapunov指数为非正数；在混沌态最大，Lyapunov指数为正数.

图2 a变化时系统(1)的Lyapunov指数与分岔Fig.2 Lyapunov Exponent and Bifurcation Diagram of System (1) with a Change

2 同步控制器设计及仿真

2.1 同步控制器设计

为了更好地设计控制器，利用系统(1)构建驱动系统

(8)

则相应的响应系统

(9)

其中u为控制信号.令系统误差为

则对应的误差系统为

(10)

令控制器的控制信号

u(t)=ae2(t)-2ae1(t).

(11)

将(11)式代入方程组(10)，得

(12)

将系统(12)作线性化处理，得到Jacbian矩阵

显然矩阵A的特征值为-a,-c,-b.根据劳斯判据可判定系统(12)为稳定性系统.

2.2 设计仿真

令q=0.9,a=20,b=4,c=32，则驱动系统(8)初值为x1(0)=11,y1(0)=10,z1(0)=13，响应系统(9)初值为x2(0)=36,y2(0)=52,z2(0)=48.对系统(8)和(9)的状态变量进行仿真,系统(8)和(9)的状态变量同步效果如图3所示，误差系统时间响应如图4所示.由图3，4可以看出，2个系统在1.5 s左右达到同步，响应速度较快.

图3 系统(8)和(9)状态变量同步效果Fig.3 Synchronization of State Values in System (8) and System (9)

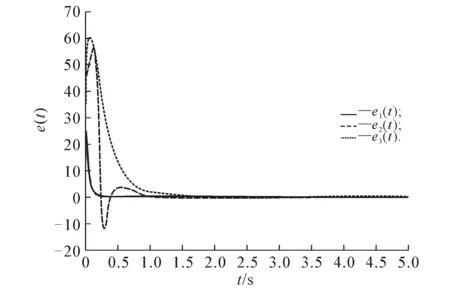
图4 误差系统时间响应Fig.4 Error System Time Response

3 在保密通信中的应用

图5 分数阶混沌保密通信系统Fig.5 Fractional Chaotic Secure Communication System

混沌掩盖是最简单的混沌通信方式，其主要以混沌同步控制器为基础，把需要发送的信息信号直接叠加在混沌信号上，利用混沌信号的伪随机特性传输信号.分数阶混沌保密通信系统如图5所示.输入信号为m(t)，m(t)=sin(2t)+3cos(20t)+2sin(10t).加密信号为分数阶系统(8)的输出信号z1(t)，则加密后的信号为s(t)=z1(t)+3m(t).加密信号与加密后的信号如图6所示.发送端与接收端的信号如图7所示，从中可知两端的信号同步.

图6 加密信号与加密后的信号Fig.6 Signal to be Encrypted and Encrypted Signal

图7 接收端与发送端的信号Fig.7 Signals Received and Transmitted

4 结语

提出了一类分数阶过渡Bao混沌系统并进行了数值仿真，从系统的分岔图和最大Lyapunov指数图两方面分析了0.9阶次Bao混沌系统的动力学特性，并说明了参数对此类混沌系统的影响.为了更好地应用分数阶混沌系统，笔者设计了该系统的同步控制器，其同步仿真与加密仿真的结果均证实了系统的可行性，为进一步研究复杂通信加密方案及其电路实现提供了新的思路.

参考文献：

[1] HILFER R.Applications of Fractional Calculus in Physics[M].New Jersey：World Scientific，2001.

[2] MANDELBRT B B.The Fractal Geometry of Nature[M].New York：Freeman,1983.

[3] LU J G.Nonlinear Observer Design to Synchronize Fractional-Order Chaotic System via a Scalar Transmitted Signal[J].Physica A:Statistical Mechanics & Its Applications，2006,359(1)：107-118.

[4] 王 震，孙 卫．分数阶Chen混沌系统同步及Multisim电路仿真[J].计算机工程与科学，2012，34(1)：187-192．

[5] WU X J.Chaos in the Fractional Order Unified System and Its Synchronization[J].Chinese Physics，2007，16(7):392-401.

[6] 贾红艳,陈增强,薛 薇.分数阶Lorenz系统的分析及电路实现[J].物理学报,2013,62(14):56-62.

[7] BAO Bocheng，LIU Zhong，XU Jianping．New Chaotic System and Its Hyperchaos Generation[J].Journal of Systems Engineering and Electronics，2009，20(6)：1 179-1 187．

[8] 刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报，2007，56(12)：6 865-6 873.

[9] 贾红艳,陈增强,薛 薇.分数阶Lorenz系统的分析及电路实现[J].物理学报,2013,62(14):56-62.

[10] 陈 恒，雷腾飞，王 震，等.分数阶Lorenz超混沌系统的动力学分析与电路设计[J].河南师范大学学报(自然科学版)，2016，44(1)：59-63.

[11] 贺少波,孙克辉,王会海.分数阶混沌系统的Adomian分解法求解及其复杂性分析[J].物理学报,2014,63(3):58-65.

[12] WANG X Y,ZHANG Y L.Modified Projective Synchronization of a Fractional-Order Hyperchaotic System with a Single Driving Variable[J].Chinese Physics B,2011,20(10):159-165.

[13] 于永光，李兰荣，孟 霞，等.分数维环式单向耦合Lorenz 系统的同步[J].北京交通大学学报，2009，33(3):103-106.

[14] 单 梁,李 军,闵富红,等.新分段分数阶混沌系统的同步控制[J].系统工程与电子技术,2010,32(10):2 198-2 202.

[15] 李 东,邓良明,杜永霞,等.分数阶超混沌Chen系统和分数阶超混沌Rssler系统的异结构同步[J].物理学报,2012,61(5):51-59.

[16] 王兴元.混沌系统的同步及在保密通信中的应用[M].北京：科学出版社，2012.