低压微网逆变器自适应谐波下垂控制策略
黄骏翅,曾 江,杨 林,黄仲龙
(华南理工大学 电力学院,广东 广州 510640)
0 引言
近年来,我国对可再生能源的开发和利用尤为重视,全面提高对可再生能源发电的支持,逐步实现能源结构的战略调整,而微网是可再生能源分布式发电规模化应用的有力解决途径[1-3]。但是,随着电力电子装置在微网中的应用和非线性负载的大量接入,导致微网公共连接点PCC(Point of Common Coup-ling)处的电压发生畸变,对接入的电力设备造成恶劣的影响。针对该问题,一般采用有源电力滤波器APF(Active Power Filter)来治理谐波,但专门的电能质量治理装置的安装成本高、功能单一,并且容量利用率低、经济性较差、推广难度大。考虑到微网中分布式电源逆变器与APF在拓扑和控制上是相似的,一般具有较大的容量裕度,且其离微网PCC处的用电设备和谐波源较近,易于就地治理,因此有学者提出利用分布式电源逆变器对微网PCC进行谐波治理,并已有了大量的研究成果[4-13]。
文献[4-8]提出了一种光伏并网和有源滤波统一控制策略,在实现最大功率点跟踪MPPT(Maximum Power Point Tracking)的前提下,检测负载电流的无功分量和谐波分量,利用逆变器的剩余容量对其进行补偿。这种策略能最大化补偿谐波源产生的谐波电流和无功功率,但需额外的电流互感器对固定谐波源进行采集,在谐波源较多或其分布较散的情况下,都需增大传感器和线路的成本;文献[9-11]提出一种分频虚拟电阻的多逆变器并联控制策略,通过减小逆变器在各次谐波频率下的等效输出电阻,有效地分担各次谐波功率,从而改善各并联逆变器输出电压的质量,但该策略的主要控制目标是各并联逆变器间的谐波环流,无法进一步补偿PCC处的谐波源电流,因此不能充分利用其容量进行谐波治理;文献[12-13]提出一种并联谐波阻尼型逆变器控制策略,该策略通过控制逆变器的输出谐波电流和谐波电压成固定比例,使逆变器在外特性上表现为纯阻性,利用虚拟谐波阻尼的分压作用有效地抑制PCC处的谐波电压,但由于逆变器输电线路阻抗的差异,难以实现各并联逆变器按容量治理谐波。
针对以上控制策略存在的不足,本文参考基波鲁棒性下垂控制[14-15]在调压调频的同时能按容量精确分配各并联逆变器功率的基本原理,提出了一种低压微网逆变器自适应谐波下垂控制策略,在无互联通信线以及负载电流传感器的情况下,实现PCC处电压谐波抑制以及各逆变器间谐波的功率分配,并在鲁棒性谐波下垂控制的基础上,设计了基于PCC处电压谐波检测的下垂系数自适应调节器,以适应不同大小的系统侧谐波源和非线性负载。
首先,将基波鲁棒性下垂控制的思想引入谐波控制上,建立和分析了鲁棒性谐波下垂控制的控制框图,并根据鲁棒性下垂控制应用至谐波控制额定工况的特殊性,对其进行简化设计,并在此基础上设计了下垂系数自适应调节策略;然后,设计了基于自适应谐波下垂控制的整体控制结构及其电流跟踪方案;最后,通过PSCAD仿真以及硬件实验对本文所提策略进行验证。
1 鲁棒性谐波下垂控制建模与优化
1.1 鲁棒性谐波下垂控制建模
多逆变器并联的典型微网等效电路见附录A中图A1,逆变器、线性负载和非线性负载共同并联在交流母线PCC上,并网运行时PCC与系统相连,本文主要针对并网场景进行设计与分析。

(1)
(2)

图1 鲁棒性谐波下垂控制结构框图Fig.1 Structure diagram of Robust harmonic droop control
一般φh很小[15],故式(1)、式(2)可分别简化为式(3)、式(4)。
(3)
(4)
(5)
ωh=mh(Qh-Qhset)+hω1
(6)
其中,ωh为无功下垂控制器的输出值,经积分后得到φh。由于Rvir_k太大会引起系统不稳定[17-18],故难以实现逆变器串联总阻抗按容量匹配。为了增大功率按容量分配的鲁棒性,在有功功率控制的前馈通道上增加积分环节,并引入PCC处谐波电压幅值负反馈抑制谐波电压[15]。整体的鲁棒性谐波下垂控制如图1所示。根据式(3)、(4),图1所示控制策略的等效框图如图2所示。

图2 鲁棒性谐波下垂控制等效框图Fig.2 Equivalent structure diagram of Robust harmonic droop control
当系统到达稳态时,积分器的输入信号等于0,同时PCC处的h次谐波频率等于逆变器的h次谐波频率,即有ωhL=hω1,结合图2有:
nh(Phset-Ph)=UhL-Uhset
(7)
Qh=0
(8)
PCC处电压幅值UhL、谐波电压设定值Uhset对于每个逆变器都相同,而各逆变器间下垂系数与其容量成反比,由式(7)可知,各逆变器的谐波功率Ph严格按照逆变器容量分配,而与线路阻值无关,由此在理论上证明了鲁棒性谐波下垂控制的有效性。至此,参照基波的鲁棒性下垂控制建立了鲁棒性谐波下垂控制的基本控制结构。
1.2 鲁棒性谐波下垂控制简化设计
从图1所示的控制框图可知,该控制策略难以实现,一方面,谐波功率的精确计算以及PCC处谐波电压的提取,都需加低通滤波器滤除其他次数谐波和基波分量,或者需采用傅里叶变换提取频谱,从而造成了闭环反馈通道的延时,严重影响系统的稳定性;另一方面,虚拟阻抗的特性由逆变器输出电流至输出电压的传递函数决定,该传递函数在高频段必存在相位滞后,导致谐波虚拟阻抗呈阻感性,无法实现谐波有功和无功的解耦控制。因此,鲁棒性谐波下垂控制要应用在实际必须做进一步的改进。现做以下简化,在无非线性负载和系统侧无谐波电势的情况下,谐波有功、无功、PCC处谐波电压均为0,以此为额定工况,可设Phset、Qhset、Uhset为0,则式(7)可简化为式(9)。
Ph=-UhL/nh
(9)
由式(9)可得逆变器入网h次谐波电流Ih的表达式如式(10)所示。
Ih=(Ph- jQh)/UhL=-1/nh
(10)
由式(10)可见,鲁棒性谐波下垂控制的控制效果与恒逆变器输出电流等效,且输出h次谐波电流幅值Ih为有功下垂系数的倒数,相位与PCC点h次谐波电压相位相反。
1.3 下垂系数自适应调节控制策略设计
有功下垂系数取决于负载有功的变化范围和PCC处电压幅值允许的范围,但负载谐波有功的变化范围难以预测,故提出下垂系数自适应调节控制策略,其控制流程图如图3所示。图中,ki为与逆变器容量成正比的固定系数,而每台逆变器的自适应下垂增量值ΔIset、h次谐波电压上阈值UhsetH、h次谐波电压下阈值UhsetL都设为相同的定值。当逆变器并联的母线与电网间的总开关合上后,逆变器同时检测到电网电压进行初始化,或所有逆变器每天定时进行初始化,即令h次谐波电流为0。当各逆变器检测到PCC处谐波电压的幅值大于UhsetH或小于UhsetL时,经一段时间的延时以确保每个逆变器都检测到上述越界信号,再根据图3所示算法对输出电流Ih进行修正,所有逆变器按容量比例同时增加或减小输出电流Ih,由式(9)和(10)可知,各逆变器谐波功率按其容量分配。下文将解释该策略调节谐波电压的机理。
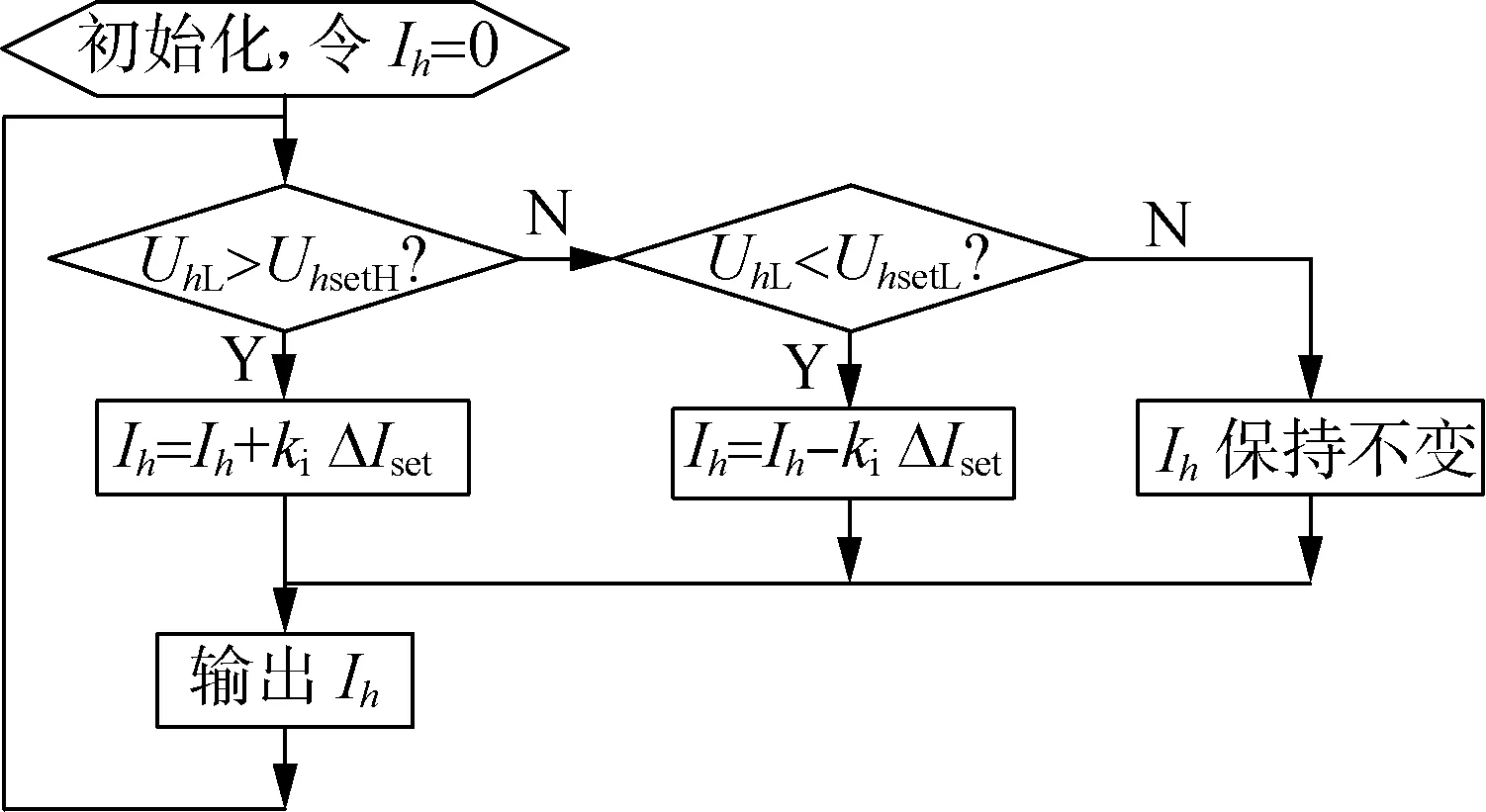
图3 下垂系数自适应调节流程图Fig.3 Flowchart of adjusting droop coefficient adaptively
附录A的图A1中PCC的右边部分,即包含系统谐波电势、系统阻抗、负载阻抗和谐波电流源的部分,可用戴维南等效电路表示,即可以用一个谐波空载电势Eheq和谐波电阻Rheq串联在PCC处表示,易得PCC处谐波有功与端电压的网络特性,如式(11)所示。
(11)
由式(11)可以看出,Ph与UhL的关系是关于UhL=Eheq/2对称、开口朝上的抛物线,如图4中曲线Pgh1(UhL)、Pgh2(UhL)和Pgh3(UhL)所示。由式(9)可得逆变器下垂特性曲线。图4中,曲线Pih1(UhL)和Pih2(UhL)为所有逆变器的总下垂特性,即为各逆变器下垂特性曲线在纵轴上的叠加,该曲线的斜率即为所有逆变器输出的h次谐波电流幅值的之和Ihsum的相反数。另外,从式(9)可以看出,该策略需占用逆变器的剩余容量,为了准确调节特定次数的谐波电压,单个逆变器只能同时治理有限次数的谐波,如同时治理典型次数5、7次的谐波。若想治理更多次数的谐波,可对PCC处的逆变器进行分组处理,每组负责治理特定的谐波。

图4 下垂系数自适应调节Fig.4 Adaptive adjustment of droop coefficient
现以图4所示的调节过程为例解释谐波电压的调节机理。
a. 当Eheq较小时,网络特性曲线为Pgh1(UhL),当Ihsum=0时,系统运行在点A,此时,谐波电压的幅值UhL>UhsetH,下垂系数自适应调节器调整下垂系数,即增大Ihsum,此时逆变器总下垂特性为Pih1(UhL),与Pgh1(UhL)交于点B,可见,点B的h次谐波电压幅值在设定的范围内。
b. 当Eheq增大、网络特性曲线为Pgh2(UhL)时,系统运行在点C,此时,h次谐波电压幅值依然在设定的范围内,可见,Eheq在一定范围内变化时,固定的Ihsum能使谐波电压控制在设定范围内。另外,类比同步发电机的一次调频下垂特性可知,在Ihsum固定的范围内可同时抑制谐波电压以及谐波有功功率的波动。
c. 当Eheq继续增大、网络特性曲线为Pgh3(UhL)时,系统运行在点D,下垂系数自适应调节控制器在检测到谐波电压过大后,增大Ihsum值,逆变器总下垂特性为Pih2(UhL),此时系统运行在点E,谐波电压控制在设定范围内。同理,当Eheq变小后,网络特性变为Pgh2(UhL),逆变器总下垂曲线调节为Pih1(UhL),系统从点E回到点C。
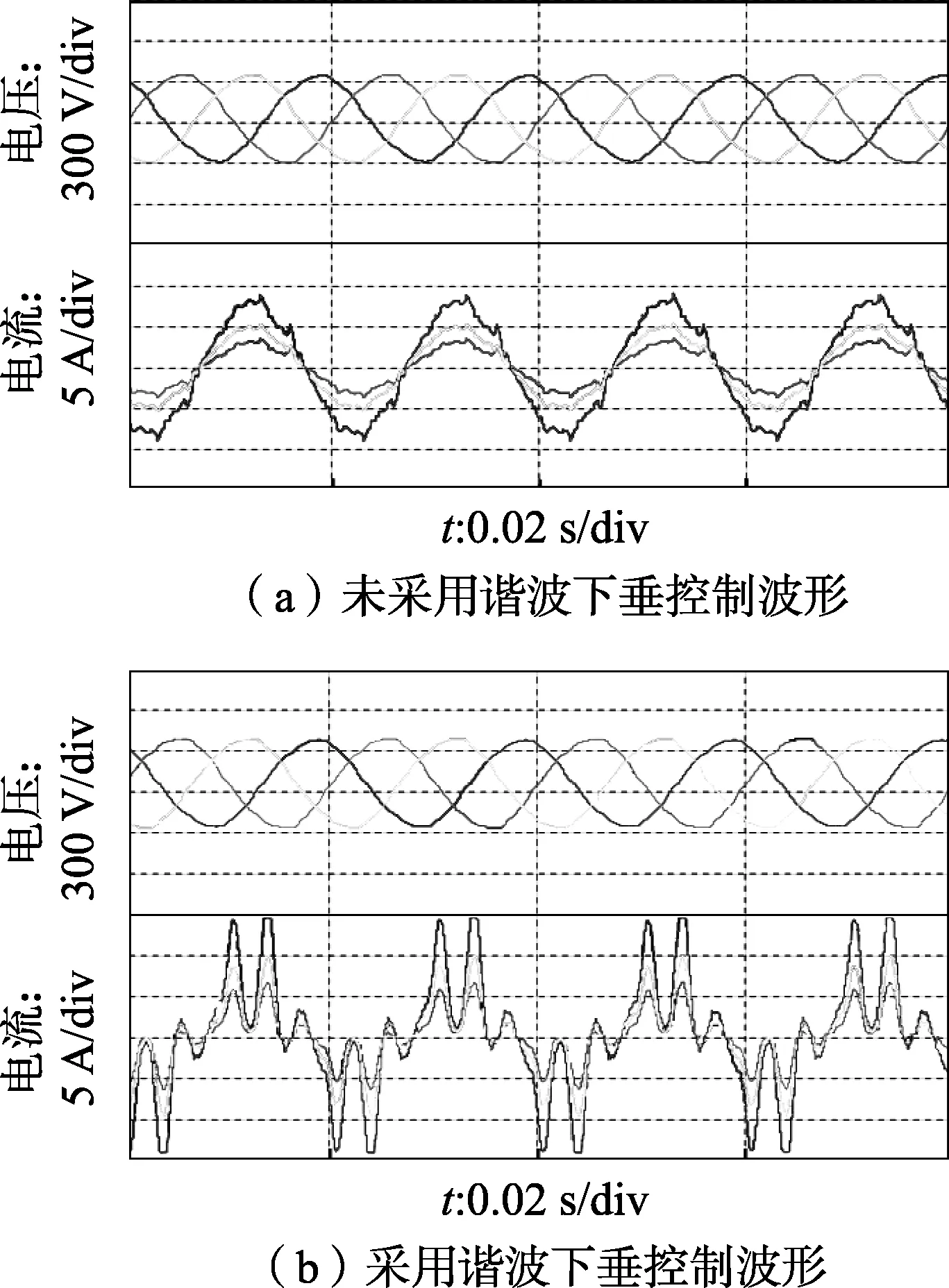
d. 另外有2种特殊情况,第一种情况是Eheq增大后逆变器检测到UhL>UhsetH而增大Ihsum值,但Eheq回到原值后UhL却未低于UhsetL,这种情况会使逆变器在同一上下阈值电压下输出较高的Ihsum值,同理Eheq先下降后回升,有可能使得逆变器运行在较低的Ihsum值;第二种情况是Eheq的增大使逆变器增大Ihsum值后又使UhL 图5 自适应谐波下垂控制系统结构框图Fig.5 Structure diagram of adaptive harmonic droop control system (12) 其中,kp为比例系数;ωc为截止频率;krh为谐振比例系数。该控制器在设定谐波频率处有较高的增益,且截止频率ωc的引入可以有效地减小电网频率偏移对逆变器输出电流的影响。另外,在多准PR控制器后引入电网电压前馈以抑制电压扰动,引入电容电流负反馈以增加系统的阻尼[19]。PCC处谐波电压的变化周期较长,而准PR控制器具有较高的动态性能,DFT又具有较高的检测速度,故本文方案能精确调节PCC处谐波电压。 根据图5所示结构框图,可求得参考电流i*至逆变器输出电流i2的开环传递函数与闭环传递函数,分别如式(13)、式(14)所示。 (13) (14) 取L1=0.74mH、L2=55μH、Cc=6.6μF、KPWM=1,综合考虑系统的稳定性和抗扰性[20],选取多准PR控制器的参数为kp=4、kr1=200、kr5=200、kr7=200,ωc=5rad/s,电容电流反馈系数kc=15。将以上参数代入式(13)、(14)可得到相应的波特图,见附录B中图B1。从图B1(a)的开环波特图可见,系统的幅值裕度为12.1dB,相位裕度为78.8°,均满足稳定性要求;从图B1(b)的闭环波特图可见,该闭环系统频率响应在基波、5次和7次谐波相对应的频率下均呈现幅值接近0、相位接近0°,可见本文所提电流跟踪算法对设定次谐波具有较高的跟踪精度。 为了验证所提控制策略的有效性,采用PSCAD仿真软件构造2条逆变电源支路、2条由不可控整流桥接电阻负载的非线性负载支路,以及用三相基波电压源、三相5、7次谐波电压源和阻抗串联等效的微网系统侧电路,其连接方式与附录A中图A1一致。其中逆变器1的容量为10kW,逆变器2容量为15kW,两者均为NPC三电平电压源型逆变器。由于逆变器直流电容电压控制不作为本文的研究对象,仿真中用2个幅值为325V的理想直流电压源并联在逆变器直流侧,基波电流指令设定为恒定值,逆变器1的基波指令电流有效值为7.5A,逆变器2的基波指令电流有效值为11.3A,kPWM经标幺化处理后为1。非线性负载支路1所接电阻为80Ω,非线性负载支路2所接电阻为20Ω,分别代表大非线性负载和小非线性负载。系统基波电势为220V,5次谐波电势为4.5V,7次谐波电势为3V,系统侧等效阻抗Zs=0.1+ j0.01Ω。多准PR控制器参数和电容电流反馈系数与第2节相同。自适应下垂控制的工作步长为0.06s。其余仿真参数如下:逆变桥侧电感L1=0.74mH,入网侧电感L2=55μH,滤波电容Cc=6.6μF,载波频率fc=20kHz,逆变器线路阻抗Zline=0.15+j0.015Ω,自适应下垂增量值ΔIset=2A,逆变器1下垂增量系数k1=1,逆变器2下垂增量系数k2=1.5,5次谐波上阈值电压U5setH=4V,5次谐波的下阈值电压U5setL=3V,7次谐波的上阈值电压U7setH=3V,7次谐波下阈值电压U7setL=2V。 图6 仿真结果Fig.6 Simulative results 仿真时间为1s,仿真过程如下:2台逆变器在0.2s 启动自适应谐波下垂控制,0.4s时合上非线性负载支路1,0.6s时合上非线性负载支路2,0.8s同时断开以上2个负载,其仿真波形如图6所示。在0.2s之前,自适应谐波下垂控制尚未启动,2台逆变器的输出谐波电流、谐波功率均为0,此时5次谐波电压为4.5V,7次谐波电压为3V。0.2s时刻,启动自适应下垂控制,2台逆变器分别调节各自的输出谐波电流,其中逆变器1的5次谐波电流为4A、7次谐波电流为2A,逆变器2的5次谐波电流为6A、7次谐波电流为3A;PCC处5次谐波电压下降至3.5V, 7次谐波电压降至2.5V。0.4s时刻,小非线性负载支路1合上,使5、7次谐波电压均有所增大,但均未超过阈值,因此,2台逆变器的谐波电流均未改变,此过程相当于下垂系数固定的常规鲁棒性下垂控制,起到抑制谐波电压和谐波功率波动的作用。0.6s时刻合上大非线性负载支路2,5次谐波电压超过上阈值,2台逆变器分别调节其5次谐波电流至6A 和9A,5次谐波电压被有效地控制在4V以内,而7次谐波电压未超过阈值所以7次谐波电流均未改变。0.8s时刻,切除2条非线性负载支路,PCC处5次谐波电压低于下阈值,2台逆变器分别调节5次谐波电流至4A和6A。整个过程中,5、7次谐波电压有效值均控制在上、下阈值之间。图6(b)中UL50和UL70分别为同样工况下未采用谐波下垂控制PCC处的5次谐波电压和7次谐波电压,从中可见,采用谐波下垂控制后,各谐波电压都有较大幅度的减小。由图6(c)、(d)可见,除了短时间的调节过程,两逆变器的谐波有功功率均按逆变器容量分配,而谐波无功功率均控制为0,符合第1节的理论。图6(e)、(f)为0.3~0.34s内2台逆变器的输出电流波形图。 图7 电压、电流波形图Fig.7 Voltage and current waveforms 图8 PCC处谐波电压变化Fig.8 Harmonic voltage at PCC 图9 逆变器谐波电流变化Fig.9 Harmonic current of inverters 为了进一步验证本文所提方法,研制了2台10kW三相三线制逆变器样机,其直流侧分别由2套340V蓄电池组经Boost电路供电,Boost电路的输入电感为0.84mH,逆变器直流侧电容Cdc1=Cdc2=150μF,LCL滤波器参数为LLCL1=0.74mH,CLCL=6.6μF,LLCL2=55μH。电流互感传感器采用Allegro公司的ACS758LCB-050B-PFF-T,而电压传感器采用电阻分压采样,两者的精度基本可以满足要求。数字控制系统的主控DSP芯片为TI公司的TMS320F28335。实验记录仪器使用3196电能质量分析仪。由于实验室没有大功率的非线性负载,受实验条件的约束,实验中用2台逆变器样机并于电网进行相关实验,PCC处不接负载,但仍可通过对电网自带背景谐波电压的抑制作用验证本文所提策略。为了突出功率分配的效果,实验中假设2台逆变器的容量比为2∶3。其中Boost电路控制蓄电池的输出功率,逆变器1为2kW,逆变器2为3kW,而逆变器直流侧电容电压由逆变器基波电流控制。自适应谐波下垂控制参数如下:5次谐波电压上阈值U5setH设为2V,7次谐波电压上阈值设为U7setH设为1.5V,5、7次谐波电压下阈值电压均设为0.5V,逆变器1下垂增量系数k1设为1,逆变器2下垂增量系数k2设为1.5,自适应下垂增量值ΔIset设为0.5A。另外,下垂系数自适应调节器的调节步长设为3s,使得3196电能质量分析仪能检测到谐波电压的调节过程,调节器在14s时刻启动。为了对比2台逆变器的输出电流,3个电流钳分别箝位在逆变器1、逆变器2和汇流线的B相输电线路,实验波形如图7所示。从图7可见,基于本文所提控制策略的逆变器不再单纯输出基波电流,还包含与需抑制谐波电压相同次数且大小与逆变器容量成比例的谐波电流。该输出电流波形与仿真中的波形有所差异,这主要是因为两者的系统谐波电阻Rheq以及所设定的谐波电压阈值均是有差异的。3196电能质量分析仪记录的调节过程如图8、9所示。14s之前,未启动谐波下垂控制,PCC处5次谐波电压和7次谐波电压均超过所设阈值;14s启动谐波下垂控制,经过3个步长的调节,谐波电压均抑制在阈值范围内。从图9可见,调节完成后2台逆变器的谐波电流均与容量成比例。谐波下垂控制使能前、后PCC处电压频谱分别如附录C中图C1和图C2所示。从图C1、图C2可知,使用本文所提控制策略后,5次谐波电压由2.65V降至1.52V、7次谐波电压由2.26V降至1.22V,两者均降至所设上阈值电压之下。从上述实验结果可见,本文所提控制策略对PCC处谐波电压产生了抑制作用,并能限制其在设定范围内。 本文提出、设计了低压微网逆变器自适应谐波下垂控制策略,通过第1节的数学建模、理论分析,初步证明该策略能使PCC处谐波电压抑制在设定范围内,并能使各逆变器按容量分配谐波功率,同时PSCAD仿真结果和实验平台的实验结果都得到了与理论分析相同的效果,进一步验证了该策略的有效性。 基于基波的鲁棒性下垂控制研究已逐渐成熟,而本文所提策略也是基于其在调压调频的同时能按容量精确分配各并联逆变器功率的基本原理进行设计的,但不同于已有文献的是:本文所提策略的控制目标是谐波电压和谐波功率,并根据鲁棒性下垂控制应用于谐波控制额定工况的特殊性进行了简化设计,在此基础上,还设计了下垂系数自适应调节策略和多准PR电流跟踪方案。 针对多台并联逆变器对PCC进行电压谐波治理的应用场合,本文所提控制策略较其他方法具有以下优点: a. 各逆变器独立、自治地参与微网谐波治理,无需通信线和负载电流传感器,节省成本,谐波治理功能即插即同; b. 可适应不同大小的系统侧谐波源和非线性负载,通过自适应控制使PCC处谐波电压抑制在设定范围内; c. 各逆变器治理谐波电压所吸收的谐波功率按容量分配。 本文所提策略在典型低压微网谐波抑制上不仅具有较高的工程价值,而且易于实现,但该策略只适用于所有逆变器都并联于同一PCC的工况,不能应用于微网其他更为复杂的拓扑结构。针对上述存在的问题,笔者下一步将结合模糊控制和谐波下垂控制进行研究,以减小本文所提策略对PCC处谐波电压反馈的依赖。 附录见本刊网络版(http:∥www.epae.cn)。 参考文献: [1] 曹一家,郑玉芳,于晶荣,等. 微电网弱约束容性等效输出阻抗逆变器控制方法[J]. 电力自动化设备,2016,36(2):1-4,10. CAO Yijia,ZHENG Yufang,YU Jingrong,et al. Weakly-constrained control of microgrid inverter with capacitive equivalent output impedance[J]. Electric Power Automation Equipment,2016,36(2):1-4,10. [2] 李鹏,窦鹏冲,李雨薇,等. 微电网技术在主动配电网中的应用[J]. 电力自动化设备,2015,35(4):8-16. LI Peng,DOU Pengchong,LI Yuwei,et al. Application of microgrid technology in active distribution network[J]. Electric Power Automation Equipment,2015,35(4):8-16. [3] KO S H,LEE S R,DEHBONEI H,et al. A grid-connected photovoltaic system with direct coupled power quality control[C]∥IECON 2006-32nd Annual Conference on IEEE Industrial Electronics. Paris,France:IEEE,2006:5203-5208. [4] 周林,曾意,郭珂,等. 具有电能质量调节功能的光伏并网系统研究进展[J]. 电力系统保护与控制,2012,40(9):137-145. ZHOU Lin,ZENG Yi,GUO Ke,et al. Development of photovoltaic grid-connected system with power quality regulatory function[J]. Power System Protection and Control,2012,40(9):137-145. [5] 吴春华,黄建明,陈卫民,等. 单相光伏并网与有源滤波的统一控制[J]. 电工技术学报,2011,26(10):103-109. WU Chunhua,HUANG Jianming,CHEN Weimin,et al. Unified control of single phase photovoltaic grid-connected and active power filter[J]. Transactions of China Electrotechnical Society,2011,26(10):103-109. [6] 张杰,郭晓霞,赵威. 光伏并网与有源滤波统一控制系统的研究[J]. 现代电力,2015,32(1):64-69. ZHANG Jie,GUO Xiaoxia,ZHAO Wei. Unified control of grid-connected photovoltaic and active power filter[J]. Modern Electric Power,2015,32(1):64-69. [7] 郭珂,曾意,刘强,等. LCL滤波器在具有有源滤波功能的光伏并网系统中的应用[J]. 电力系统保护与控制,2013,41(3):73-79. GUO Ke,ZENG Yi,LIU Qiang,et al. Application of LCL-filter in photovoltaic grid-connected system with active power filter function[J]. Power System Protection and Control,2013,41(3):73-79. [8] 谭兴国,冯高明,王辉,等. 兼顾有源滤波的三相四开关光伏并网逆变器[J]. 高电压技术,2014,40(11):3590-3596. TAN Xingguo,FENG Gaoming,WANG Hui,et al. Three-phase four-switch grid-connected photovoltaic inverter combined with active power filter[J]. High Voltage Engineering,2014,40(11):3590-3596. [9] 彭自强,罗安,陈燕东,等. 基于分频虚拟电阻的多逆变器并联控制策略[J]. 电网技术,2013,37(11):3276-3280. PENG Ziqiang,LUO An,CHEN Yandong,et al. A frequency-divided virtual resistance based control strategy for multi parallel inverters[J]. Power System Technology,2013,37(11):3276-3280. [10] WANG X,BLAABJERG F,CHEN Z. Autonomous control of inverter-interfaced distributed generation units for harmonic current filtering and resonance damping in an islanded microgrid[J]. IEEE Transactions on Industry Applications,2014,50(1):452-461. [11] WANG X,BLAABJERG F,CHEN Z. Synthesis of variable harmonic impedance in inverter-interfaced distributed generation unit for harmonic damping throughout a distribution network[J]. IEEE Tran-sactions on Industry Applications,2012,48(4):1407-1417. [12] HE Jinwei,LI Yunwei,BOSNJAK D,et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transactions on Power Electronics,2013,28(1):234-246. [13] AKAGI H. Control strategy and site selection of a shunt active filter for damping of harmonic propagation in power distribution systens[J]. IEEE Transactions on Power Delivery,1997,12(1):354-363. [14] 吕志鹏,罗安. 不同容量微源逆变器并联功率鲁棒控制[J]. 中国电机工程学报,2012,32(12):35-42. LÜ Zhipeng,LUO An. Robust power control of paralleled micro-source inverters with different power ratings[J]. Proceedings of the CSEE,2012,32(12):35-42. [15] 陈燕东,罗安,龙际根,等. 阻性逆变器并联环流分析及鲁棒下垂多环控制[J]. 中国电机工程学报,2013,33(18):18-29. CHEN Yandong,LUO An,LONG Jigen,et al. Circulating current analysis and robust droop multiple loop control method for parallel inverters using resistive output impedance[J]. Proceedings of the CSEE,2013,33(18):18-29. [16] DE BRABANDERE K,BOLSENS B,VAN dEN KEYBUS J,et al. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics,2007,22(4):1107-1115. [17] 张庆海,彭楚武,陈燕东,等. 一种微电网多逆变器并联运行控制策略[J]. 中国电机工程学报,2012,32(25):126-132. ZHANG Qinghai,PENG Chuwu,Chen Yandong,et al. A control strategy for parallel operation of multi inverters in microgrid[J]. Proceedings of the CSEE,2012,32(25):126-132. [18] LI Y W,KAO C N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid[J]. IEEE Transactions on Power Electronics,2009,24(12):2977-2988. [19] 雷亚雄,李建文,李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制,2014,42(12):44-50. LEI Yaxiong,LI Jianwen,LI Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Protection and Control,2014,42(12):44-50. [20] 王亮,王冰,黄存荣. 基于多PR控制的并网逆变器设计与参数整定[J]. 电网与清洁能源,2014,30(7):45-51. WANG Liang,WANG Bing,HUANG Cunrong. Design and parameter tuning of grid-connected inverters based on multi-resonant PR controller[J]. Power System and Clean Energy,2014,30(7):45-51.
2 基于谐波下垂控制的电流跟踪方案

3 仿真与实验



4 结论

