基于双储能系统的主动配电网储能配置

凌开元,赵乐冰,张新松，吴 涵，袁 越

(1. 河海大学 能源与电气学院，江苏 南京 210098；2. 南通大学 电气工程学院，江苏 南通 226019)

0 引言

传统配电网正向拥有多可控单元、高比例可再生能源渗透的主动配电网ADN(Active Distribution Network)转变。与传统配电网不同的是，ADN将储能设备、分布式能源DG(Distributed Generator)、可调负荷等视为可控单元，并对其进行主动控制与综合调度，实现能量的最优管理[1]。其中，储能系统由于具有快速调节功率的能力与兼具供蓄的特点，对ADN运行有明显的支撑和调节作用，是ADN实现可控单元灵活协调的关键和系统运行优化的重要手段。此外，储能系统还可有效改善DG出力的波动性与不确定性导致的电压越限、峰谷差过大等一系列问题。显然，储能配置是否合理将直接影响ADN对DG的主动管理能力及网络运行的经济性[2]，结合优化运行策略研究ADN中储能的优化配置，可以最大限度发挥储能对ADN的支撑作用，提升储能的应用前景。储能设备特性主要由以下参数确定：额定功率、额定容量、接入位置、爬坡率、响应间隔、响应频率[3]。目前储能优化配置主要针对前3个参数进行优化。

国内外学者已对ADN中储能的优化配置问题进行了相关研究。文献[4]提出了基于风力发电和电池储能配合的配电网有功-无功最优潮流模型，为储能优化配置问题奠定了基础；文献[5-6]从储能提高DG消纳率、降低线损及提高电压稳定性的角度进行储能优化配置。目前储能的高成本是制约其大规模应用的主要因素，因此如何降低成本是储能优化配置的一个主要目标。文献[7]基于储能全寿命周期成本建立了配电网中蓄电池储能的优化配置模型，并比较了不同材料电池的经济效益；文献[8]计及配电网中不同投资主体的利益，将储能的投资与运行成本相解耦；文献[9]在进行储能配置时考虑了电池的使用寿命并建立了电池使用寿命的量化模型。但上述文献仅小幅提升了储能的经济性，而未显著减少储能的成本。文献[10]针对风-储混合电站，提出使用2组储能系统分别处于充电和放电状态，用于平抑风功率的正、负波动分量，可以大幅降低储能充放电循环次数，有效延长储能使用寿命。然而该策略会造成储能配置容量增加从而加大储能投资成本，且文中只根据储能额定功率对其进行了简单定容，并未研究该策略下的储能容量优化。

针对上述问题，本文从储能经济性角度出发，综合考虑储能使用年限与全寿命周期成本，提出一种基于双储能系统的主动配电网储能优化配置方法，结合运行策略建立两阶段优化模型，分别用于确定储能的接入位置与额定容量。算例分析结果表明本文所提储能优化配置方法可以有效减少ADN中储能的总年成本，提高储能经济性。

1 储能系统选址模型

1.1 目标函数

储能系统在电力系统中各场合应用的技术优势已得到论证，但当前储能的单位容量成本较高，导致储能接入后盈利空间有限，制约了其大规模应用。为满足工程应用的需求，将ADN中储能安装的总容量作为目标值，即求解满足电网安全运行要求的最小储能配置容量时储能的接入位置及该情况下对应的储能充放电策略。目标函数如下：

(1)

其中，z为配电网节点数目；Eess,i为节点i接入的储能额定容量。

1.2 约束条件

约束条件主要包含DG、储能系统及潮流的相关约束，变量为各时段的DG出力与储能充放电功率，因此可优化得到储能的运行策略。

(1) DG出力约束。

(2)

其中，PDG,t、QDG,t分别为DG在t时段的有功、无功功率；PDGtheory,t、QDGtheory,t分别为DG在t时段理论有功及无功最大值。

(2) 储能充放电功率约束及储能荷电状态SOC(State Of Charge)约束。

(3)

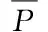
相邻时段储能SOC满足以下耦合关系：

(4)

其中，SoCt为储能在t时段初的SOC；ηchar、ηdis分别为储能的充电、放电效率，分别取0.88、0.9；Fchar,t、Fdis,t分别为储能的充电、放电状态，为0、1变量；Δt为仿真时间步长，本文取15min。储能的充放电状态不能同时存在，即满足如下约束：

Fdis,t+Fchar,t≤1Fdis,t,Fchar,t∈(0,1)

(5)

而储能应避免过充过放，即：

SoCmin≤SoCt≤SoCmax

(6)

其中，SoCmax、SOCmin分别为储能SOC最大、最小值。

移动储能在一个完整调度周期内，应使能量守恒以保证调度的可持续性：

SoCini=SoCend

(7)

其中，SoCini、SoCend分别为储能在一个调度周期起始及结束时的SOC。

(3) 配电网潮流约束。

节点电压约束如下：

(8)

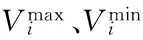
潮流等式约束如下：

(9)

其中，Pi,t、Qi,t分别为t时段节点i的有功、无功净注入功率；Gij为节点i、j之间的电导；θij为节点i、j的电压相角差；Bij为节点i、j之间的电纳。

线路功率约束如下：

(10)

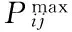
2 储能容量优化模型

为满足大量DG接入下电网的安全运行要求，储能在运行时可能会在充电与放电状态之间频繁转换，致使储能循环寿命快速耗尽，从而极大降低储能的经济性。因此，在对储能进行配置时有必要建立循环寿命损耗模型，并在此基础上结合储能运行策略与全寿命周期成本进行储能容量的优化。

2.1 储能循环寿命损耗模型

蓄电池循环寿命受到例如温度、峰值电流、充放电循环次数等因素的影响[11]。而放电深度DOD(Depth Of Discharge)也能直接影响其循环寿命，记为Ddis。本文主要考虑放电深度与循环次数对循环寿命的影响。

在各种电池储能材料中，锂电池具有充放电效率高、循环寿命长、兼具高比能量和高比功率等特性，被认为是最有前景的电池材料，是电力系统储能材料的理想选择[12]。因此，本文将锂电池储能作为研究对象。文献[13]实验测得锂电池放电深度与其循环寿命的关系曲线如图1所示。采用4阶多项式函数对该曲线进行拟合，得到函数关系如下：

(11)

其中，N(Ddis)为该放电深度下储能循环寿命。

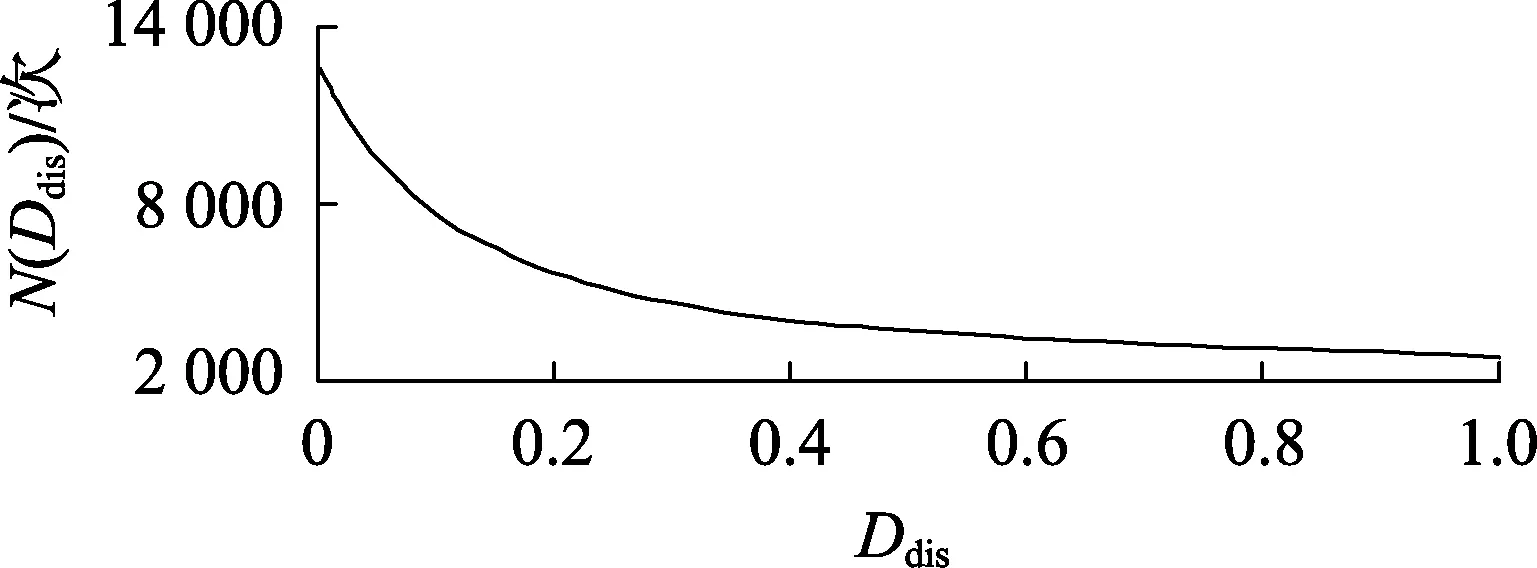
图1 循环寿命与放电深度的关系Fig.1 Relationship between cycle life and depth of discharge

储能运行工况可视作一系列不同放电深度充放电循环的线性组合，将运行工况分解为多个放电深度不同的工况，分别计算分解后各工况下的储能循环寿命，再根据储能在各对应工况下的循环次数，直接线性叠加求出储能循环寿命损耗。储能在运行中循环寿命损耗可按下式计算：

(12)

其中，n为该放电深度下储能的循环次数。

储能的充放电循环次数与对应的放电深度可通过雨流计数法进行统计[14]，再由式(11)、(12)便可得到储能在运行过程中的循环寿命损耗情况。当L=1时，则视作储能寿命耗尽，此时储能需进行更换。

2.2 双储能系统运行策略

在第1节求解得到储能接入节点位置及优化出力策略后，在各储能接入节点配置2组容量相同的储能，记为ESS1、ESS2。采用第1节优化的储能充放电策略来决定双储能系统的运行策略，2组储能采取交替工作方式，分别承担充电与放电工作，当其中一组储能达到SOC上下限则切换2组储能的充放电状态。其具体切换流程如图2所示。图2中，t1、t2分别为一个仿真时段的起始与结束时刻，假设该时段ESS1达到其SOC的上限，且ESS1在该时段最大允许功率小于运行策略要求功率，则在该时段需由ESS1与ESS2共同提供系统所需的储能充放电功率(t1～t2为共同充电)，即ESS2提前一个时段切换充放电状态，此时段2组储能充放电状态相同，下一时段ESS1切换充放电状态，ESS2充放电状态不变；某组储能达到SOC允许值下限时(如图2中t3、t4中间时段)同理。该运行策略可使双储能接入下储能各时段的总充放电功率与第1节优化运行策略要求完全一致。

图2 双储能系统充放电转换策略Fig.2 Charge-discharge change strategy of double-storage system

2.3 储能全寿命周期成本

储能全寿命周期成本是指在寿命周期内，储能投资、维修及保障等费用的总和。储能全寿命周期成本主要由一次投资成本与运行维护成本组成，其中一次投资成本为储能额定容量与额定功率的函数，其表达式为：

(13)

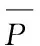
储能运行维护成本为其额定容量的函数，且与储能运行周期有关，其表达式为：

(14)

其中，Cm为储能单位充/放电功率的年运行维护成本；ir为通货膨胀率；dr为贴现率；y为储能使用年份；T为储能寿命周期。

2.4 储能容量优化模型

由于双储能运行策略中充放电工作由2组储能分别承担，因此可有效减少储能循环次数。循环次数的减少程度与储能容量直接相关。接入储能的容量越大，循环次数越少，储能使用寿命越长。但因储能单位容量造价较高，若单纯为降低储能循环次数而配置过大容量的储能将极大增加其一次投资成本，即使在使用寿命增加的情况下同样会降低其经济性，同时过大的一次投资成本也可能会超出电网的承受范围。因此需在综合考虑储能全寿命周期成本与使用寿命的基础上对储能容量进行进一步优化，将储能经济性最大化。

据此，本文将储能系统全寿命周期成本分摊至寿命周期的每一年，以储能使用寿命内配电网中储能年成本之和最小为目标函数对储能容量进行优化，目标函数表达式如下：

(15)

3 求解流程

本文ADN中储能优化配置分为两阶段进行，对应选址与定容2个优化问题。第一阶段优化求解第1节选址模型，确定储能的接入位置及对应的充放电策略；第二阶段在第一阶段求得的接入位置接入2组储能，首先根据第一阶段求得的充放电策略确定双储能系统运行策略，然后以储能年成本最小为目标对储能容量进行优化，确定最后的储能规划方案。第一阶段优化需求解时序耦合的最优潮流问题，从目标函数和约束条件可以看出，该模型属于混合整数非线性规划MINLP(Mixed Integer NonLinear Programming)。本文采用GAMS软件中的DICOPT求解器配合CPLEX和IPOPTH求解器对该模型进行求解；第二阶段采用粒子群优化算法进行求解，在粒子群优化算法内部利用雨流计数法计算储能循环次数及对应的放电深度。求解流程如图3所示。

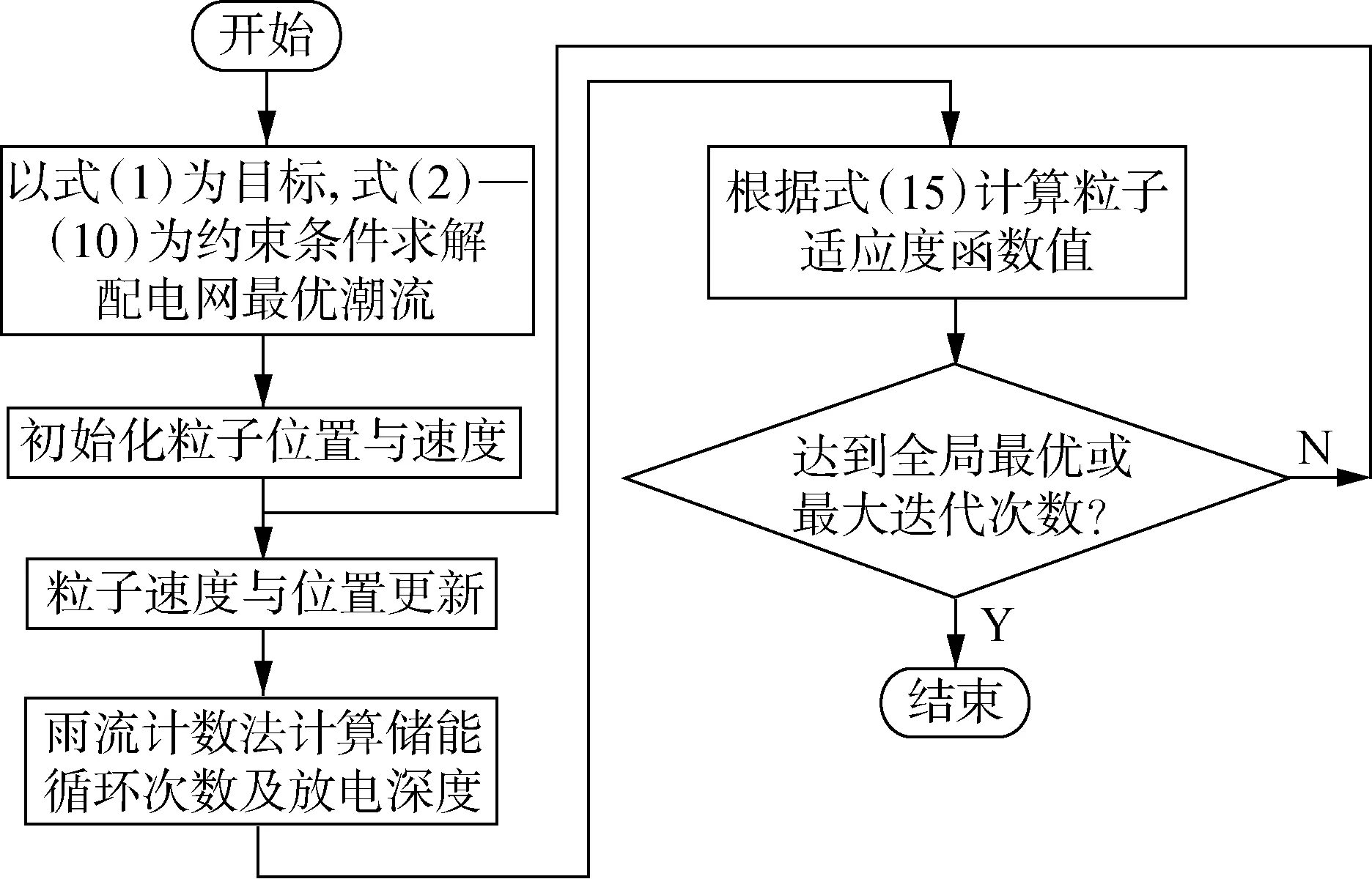
图3 储能规划求解流程图Fig.3 Flowchart of storage planning solving

4 算例分析

4.1 算例参数

本文采用如图4所示的改进IEEE 33节点馈线系统为分析对象。该系统母线额定电压为10kV，配电网电压偏差标准为±7%[15]。配电网负荷最大值为(2.981+j1.780)MV·A。节点5、16、27接入分布式光伏，容量分别为1.63MW、2.45MW、3.67MW。假设最多只能在2个节点接入储能系统，接入储能系统的待选节点为节点2—33。储能系统选用锂电池储能，参数Ce=210$/(kW·h)，Cp=428$/kW，Cm=10$/(kW·a)。设储能SOC上限为0.9、下限为0.1。通货膨胀率为1.5%，贴现率为9%。

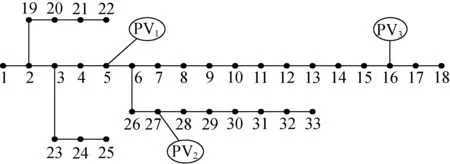
图4 改进的IEEE 33节点配电网系统Fig.4 Modified IEEE 33-bus distribution network

由于样本数据的选择并不影响本文储能优化配置方法，故算例选择典型日代表配电网运行情况以验证本文方法的有效性。

4.2 配置结果

设定粒子群最大迭代次数为100，种群规模为50，学习因子均取1.5。首先利用GAMS求解第一阶段优化问题获得储能接入位置，再利用粒子群优化算法进行第二阶段优化求解储能接入容量，得到两阶段储能配置方案分别如表1、表2所示，对应的储能典型日优化运行SOC曲线分别如图5、图6所示。

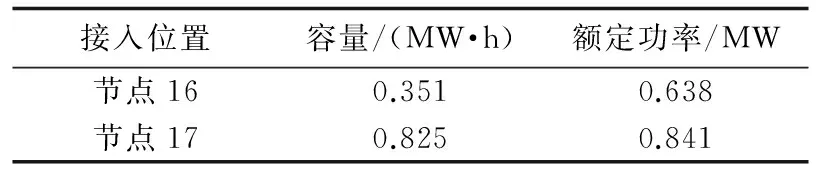
表1 第一阶段优化储能配置结果Table 1 Storage configuration results of first stage optimization

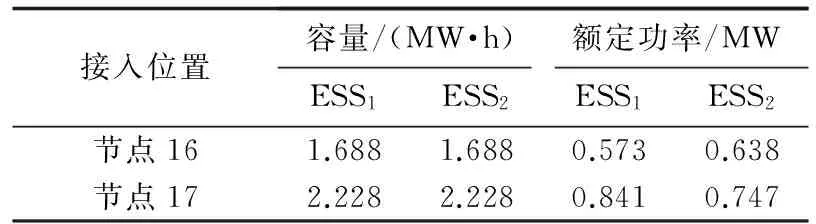
表2 第二阶段优化储能配置结果Table 2 Storage configuration results of second stage optimization

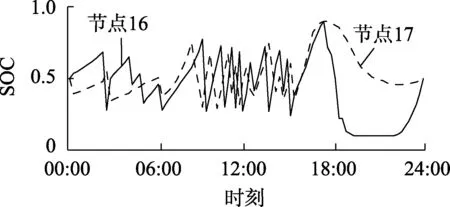
图5 第一阶段优化典型日储能SOC曲线Fig.5 Typical daily storage SOC curve of first stage optimization

图6 第二阶段优化典型日储能SOC曲线Fig.6 Typical daily storage SOC curve of second stage optimization

根据第一阶段优化结果，储能应配置在节点16、17。根据第二阶段优化结果，在节点16、17各配置2组容量相等的储能，首先进行充电的储能记为ESS1，首先进行放电的储能记为ESS2，节点16、17储能配置总容量分别为3.376MW·h、4.456MW·h。

从图5、图6中可以看出，若节点16、17各接入一组储能，则储能运行时充放电循环次数较多，由雨流计数法统计得储能在一个典型日内循环次数分别为13.5、12，如此储能循环寿命将会快速耗尽；而基于双储能策略进行第二阶段优化后，由于ESS1、ESS2交替承担充电与放电工作，循环次数大幅降低，有效延长了储能的使用寿命。且由于需其中一组储能到达SOC限值时才改变充放电状态，每组储能容量利用效率仍维持在较高水平。

优化后的储能运行年限和年成本如表3所示。综合表1—3可以看出，虽然第二阶段容量优化后各节点配置的储能容量较第一阶段结果有了较大幅度增长，全寿命周期成本增加，但由于双储能策略增加了储能的使用寿命，且降低了其中一组储能的额定功率，其年成本相比于第一阶段结果大幅降低，其中节点16储能年成本下降67.37%，节点17储能年成本下降60.60%，总计储能年成本下降63.68%。同时，该储能规划方案的一次投资成本对电网而言在其承受范围之内，即该方案在工程上是可行的。算例分析结果表明只要容量配置得当，本文基于双储能系统的ADN储能配置方法可以在储能全寿命周期成本增加的情况下通过延长储能使用寿命降低其年成本，有效提高储能的经济性。

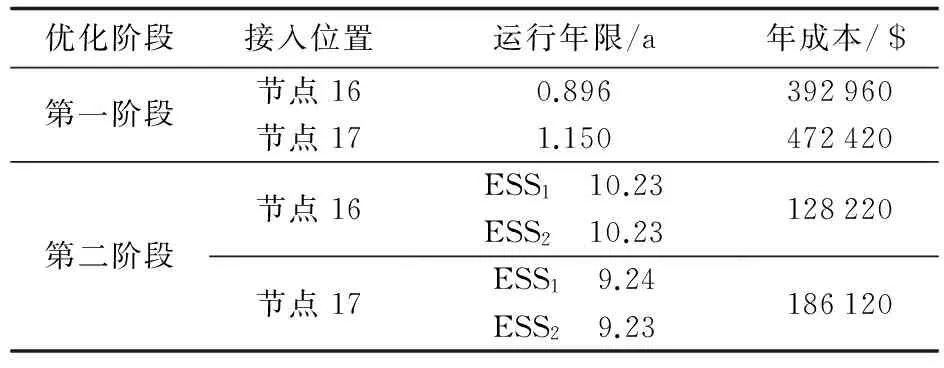
表3 储能运行年限与年成本Table 3 Operation age limit and annual cost of storage

5 结论

本文提出了一种基于双储能系统的ADN储能优化配置方法，得出以下结论：

a. ADN中DG的间歇性与波动性会使配电网电压存在越限风险，通过配置储能可有效解决电压越限问题；

b. 使用双储能系统可降低储能循环次数，增加使用寿命，但会增加储能容量从而增加投资成本，对其进行容量优化配置后可降低储能成本；

c. 本文在计算储能循环寿命损耗时考虑了循环次数及放电深度，在以后研究中可以综合考虑温度、峰值电流等因素的影响进一步精确循环寿命损耗模型，提高配置的合理性。

参考文献：

[1] 尤毅,刘东,钟清,等. 主动配电网优化调度策略研究[J]. 电力系统自动化,2014,38(9)：177-183.

YOU Yi,LIU Dong,ZHONG Qing,et al. Research on optimal schedule strategy for active distribution network[J]. Automation of Electric Power Systems,2014,38(9)：177-183.

[2] 张沈习,李珂,程浩忠,等. 间歇性分布式电源在主动配电网中的优化配置[J]. 电力自动化设备,2015,35(11)：45-51.

ZHANG Shenxi,LI Ke,CHENG Haozhong,et al. Optimal allocation of intermittent distributed generator in active distribution network[J]. Electric Power Automation Equipment,2015,35(11)：45-51.

[3] OLDEWURTEL F,BORSCHE T,BUCHER M,et al. A framework for and assessment of demand response and energy storage in power systems[C]∥IREP Symposium Bulk Power System Dynamics and Control. Rethymno,Greece：[s.n.],2013：1-24.

[4] GABASH A,LI P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage[J]. IEEE Transactions on Power Systems,2012,27(4)：2026-2035.

[5] TANT J,GETH F,SIX D,et al. Multiobjective battery storage to improve PV integration in residential distribution grids[J]. IEEE Transactions on Sustainable Energy,2013,4(1)：182-191.

[6] HUNG D Q,MITHULANANTHAN N,BANSAL R C. Integration of PV and BES units in commercial distribution systems considering energy loss and voltage stability[J]. Applied Energy,2014,113(2)：1162-1170.

[7] 向育鹏,卫志农,孙国强,等. 基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J]. 电网技术,2015,39(1)：264-270.

XIANG Yupeng,WEI Zhinong,SUN Guoqiang,et al. Life cycle cost based optimal configuration of battery energy storage system in distribution network[J]. Power System Technology,2015,39(1)：264-270.

[8] 沈欣炜,朱守真,郑竞宏,等. 考虑分布式电源及储能配合的主动配电网规划-运行联合优化[J]. 电网技术,2015,39(7)：1913-1920.

SHEN Xinwei,ZHU Shouzhen,ZHENG Jinghong,et al. Active distribution network planning-operation co-optimization considering the coordination of ESS and DG[J]. Power System Technology,2015,39(7)：1913-1920.

[9] 韩晓娟,程成,籍天明,等. 计及电池使用寿命的混合储能系统容量优化模型[J]. 中国电机工程学报,2013,33(34)：91-97.

HAN Xiaojuan,CHENG Cheng,JI Tianming,et al. Capacity optimal modeling of hybrid energy storage systems considering battery life[J]. Proceedings of the CSEE,2013,33(34)：91-97.

[10] 张新松,顾菊平,袁越,等. 基于电池储能系统的风功率波动平抑策略[J]. 中国电机工程学报,2014,34(28)：4752-4760.

ZHANG Xinsong,GU Juping,YUAN Yue,et al. Strategy of smoothing wind power fluctuation based on battery energy storage system[J]. Proceedings of the CSEE,2014,34(28)：4752-4760.

[11] SAUER D U,WENZL H. Comparison of different approaches for lifetime prediction of electrochemical systems-using lead-acid batteries as example[J]. Journal of Power Sources,2008,176(2)：534-546.

[12] 户龙辉. 锂离子电池储能系统建模及其对电网稳定性影响研究[D]. 长沙：湖南大学,2014.

HU Longhui. Research on modeling of lithium-ion battery energy storage system and its impact on the stability of power system[D]. Changsha：Hunan University,2014.

[13] LUNZ B,WALZ H,SAUER D U. Optimizing vehicle-to-grid charging strategies using genetic algorithms under the consideration of battery aging[C]∥IEEE Vehicle Power and Propulsion Conference. Chicago,USA：[s.n.],2011：1-7.

[14] SCHALTZ E,KHALIGH A,RASMUSSEN P O. Influence of battery/ultracapacitor energy-storage sizing on battery lifetime in a fuel cell hybrid electric vehicle[J]. IEEE Transactions on Vehicular Technology,2009,58(8)：3882-3891.

[15] 中国国家标准化管理委员会. 电能质量 电力系统频率偏差：GB/T 12325—2008[S]. 北京：中华人民共和国国家质量监督检疫总局,2009.