模压工艺参数对聚酰亚胺树脂压缩强度的影响及其数学模型的建立

方 琳,BURYA A I,俞鸣明,任慕苏,KALINICHENKO C B,EREMINA E A

目前,10%～15%的机械及其组件是由于强度不足而导致损坏,因此使用当代技术提高材料的耐久性已成为提高其可靠性和延长其使用寿命的首要任务.

20世纪90年代初,聚合物材料成为取代金属材料的最佳选择,而聚酰亚胺是一种取代机械装置中活动联接金属构件的最有前景的材料.聚酰亚胺是以酰亚胺环为特征结构的聚合物,具有突出的耐热性,优良的机械、电学及稳定性能等优点,其各类制品已广泛应用于航空航天、电子电工、汽车、精密仪器等诸多领域[1-5].

随着航空航天、汽车,特别是电子工业的持续快速发展,迫切要求设备具有小型、轻量、高功能和高可靠性的特点,而聚酰亚胺所具有优异性能可以充分满足上述要求.据预测，聚酰亚胺的需求量将以每年6.5%的速度递增,其发展前景非常广阔.采用模压法制备聚酰亚胺材料已成为国内外研究的热点[6-7].本工作研究了聚酰亚胺树脂的制备工艺参数对其性能的影响,并建立了这些工艺参数与性能的数学模型.

1 实验材料及方法

1.1 原材料

可熔性聚酰亚胺模塑粉(YS-20),200～300目.

1.2 制备过程

将粉末状聚酰亚胺烘干待用,以防止降低成型制品的强度以及形成表面缺陷(裂纹、气泡等).通过手动液压机完成预成型件的压片,并将压制好的预成型件置于烘箱(DHG-9075A)中,在323～473 K温度下干燥1.5～2.0 h.由于干燥会对预成型件的尺寸产生影响,因此对比最终脱模成品,预成型件的体积约1%～2%.将干燥好的预成型件立即装入已预热至653±5 K的模压设备中.首先,在无压力下预热10～30 min;然后,在此温度下将压力升至60 MPa,保压10 min;最后,冷却至523 K,脱模得到试样.

1.3 测试与表征

在Zwick/Roell公司Z020试验机上测试试样的压缩强度,测试温度为293 K,变形速率为1 mm/min,取3个平行样.

2 实验结果与讨论

2.1 工艺参数对聚酰亚胺树脂压缩强度的影响

在聚酰亚胺树脂模压成型过程中,模压参数对材料的压缩强度影响显著,其中以成型温度和无压力保温时间的影响较大.本工作设计了几组实验,研究了这2个工艺参数对材料压缩强度的影响,结果如表1和2所示.

表1 成型温度对聚酰亚胺树脂压缩强度的影响Table 1 Infl uence of molding temperature on compressive strength for polyimide resin

由表1可见,当成型温度为653 K时,聚酰亚胺树脂的压缩强度最大.由表2可见,当无压力保温时间为25 min时,聚酰亚胺树脂的压缩强度最大.因此,当成型温度为653 K、无压力保温时间为25 min时,聚酰亚胺树脂的压缩强度达到最大值.

1.3 图像处理及分析 利用CT数据对PET图像进行衰减校正。PET图像重建采用滤波反投影法。CT重建采用标准重建法，矩阵512×512，重建层厚1.25 mm。

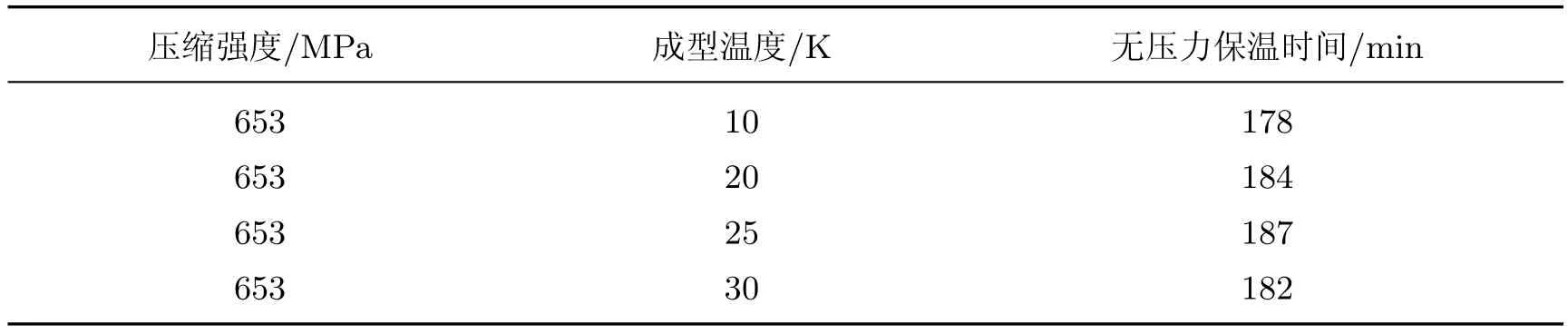
表2 无压力保温时间对聚酰亚胺树脂压缩强度的影响Table 2 Infl uence of non-pressure duration time on compressive strength for polyimide resin

2.2 数学模型的建立

在材料压制过程中,工艺参数能显著影响产品的最终性能,因而可获取工艺与性能的多元二次回归方程.为减少实验周期,本工作采用中心复合设计法,评估了成型工艺参数(成型温度、无压力保温时间)对聚酰亚胺树脂压缩强度的影响.假设二者满足关系式:y=f(x1,x2),其中x1是成型温度(T/K),x2是当成型温度为常数时,聚酰亚胺树脂的无压力保温时间(τ/min).每个因素设3个水平,实验因素和水平以及实验安排和结果如表3和4所示.

表3 因素和水平Table 3 Factors and levels

表4 实验安排与结果Table 4 Experimental arrangements and results

根据实验安排一共进行了N=NR+2n+1=9次实验,其中NR是计划中心实验数,n是因子数.每一个实验重复3次(R=3),随机去除系统误差.压缩强度与工艺参数的数学模型通过回归方程表达,确定T与τ的关系,多元二次方程式的表达如下:

在获得实验数据的基础上计算函数响应平均值yj,即

计算重复离散性,即

以及平行实验离散性Sj2,即

并通过柯赫林准则检验平行实验数据离散的一致性:

在置信度P=0.95下,将计算得到的Gp值与查表(f1=k−1=2,N=9)得到的值相比较,发现Gp=0.331小于查表得到的值(0.478).因此,平行实验离散性具有一致性.

本工作中实验误差计算公式如下:

回归方程系数的计算公式如下:

各项指标经统计学处理,拟合得到如下的多元二次回归方程:

通过方差分析来评估回归方程系数b0,b1,b2,b12,b11,b22的统计显著性和误差,其系数误差的确定公式为

置信区间Δbi的确定公式为

选取自由度N(n−1)=18和置信度P=0.95时的临界值tkp,当其满足条件:

时,则该回归系数显著.基于此,方程式(7)中的系数除b2和b22之外都是显著的.删去没有显著影响的因素,拟合方程式(8)变为

本文根据近两年湖南省不动产统一基础数据数字线划图成果进行过程质量检查及验收情况，对发现的较为突出的典型性问题以及普遍性问题进行总结和分析，找出生产过程中的关键节点及薄弱环节，旨在从生产环节尽量杜绝这些问题的出现，确保我省不动产数字线划图数据完整、真实、可靠。

由拟合方程式(8)计算得到yjp,并与实验测试值yj计算偏差,具体公式为

式中,B是拟合方程具有显著性系数的个数,其偏差与自由度f=N−B=5相关.

计算得到的参数值如表5所示,通过弗希拉准则来检验方程式(7)的显著性,并通过S2与S2b的比值来表征,即

当置信度P=0.95,自由度f=3和f2=16时,Fp=1.853,小于查表得到的值(3.16),所以拟合方程式(8)是显著的.

表5 根据Fisher试验的标准方程式评估实用性得到的计算值Table 5 Calculated values for the evaluation of the adequacy of the equations of Fisher test

通过实验设计能减少计算回归方程所需的实验次数.通过获得的回归方程来描述聚酰亚胺树脂的压缩强度与工艺参数之间的关系,结果如图1所示.可见,单纯从图1中确定聚酰亚胺压缩强度的最佳条件比较复杂,但将变量x1和x2从−1～1以0.1为间隔代入方程式(12)中时,即可准确地确定最值点.当x1=x2=0.5时,聚酰亚胺树脂的压缩强度达到最大值.

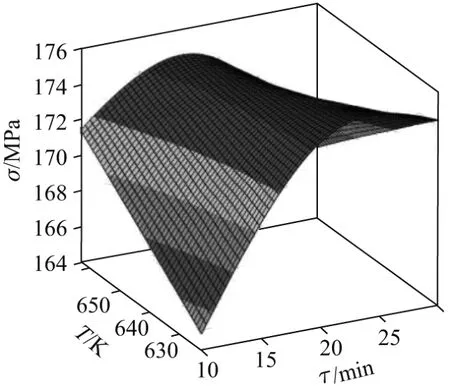
图1 成型温度、无压力保温时间与压缩强度的三维图Fig.1 3D map of molding temperature,non-pressure duration time and compressive strength

3 结束语

在本实验设计中发现,热压成型过程中的成型工艺参数会显著影响聚酰亚胺树脂的压缩强度.当成型温度为653 K、无压力保温时间为25 min时,聚酰亚胺树脂的压缩强度达到最大值.通过正交中心复合设计,经统计学处理,拟合得到的多元二次方程式为y=174.72+1.50x1−4.74x1x1−3.25x1x2.在本工作研究范围内,该方程式能充分描述聚酰亚胺树脂的压缩强度特性.