一类积分型Cauchy中值定理的再研究

杜争光



一类积分型Cauchy中值定理的再研究

杜争光

（陇南师范高等专科学校 数学系，甘肃 成县 742500）

对一类积分型Cauchy中值定理做了进一步的研究，得到了一个更加一般的结果，并对该定理“中间点”的渐进性做了讨论，推广了已有的成果.

中值定理；中间点；渐进性

1 引言及主要引理

Cauchy中值定理是微积分学中的重要定理之一. 近几年，大量文献资料对Cauchy中值定理进行了研究，取得了一系列成果. 文献[1]讨论了一类积分型的Cauchy中值定理，得到了一些有用的结论. 文献[2]再次研究了该类型的中值定理，得到了更加一般性的结论. 文献[3]讨论了广义的Cauchy中值定理，并对其“中间点”的渐进性进行了研究，也取得了一些成果.

2 主要结果

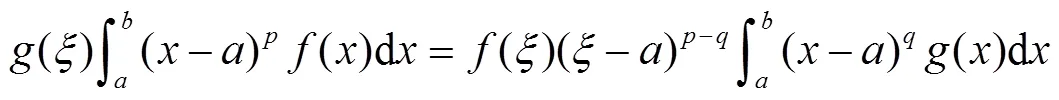
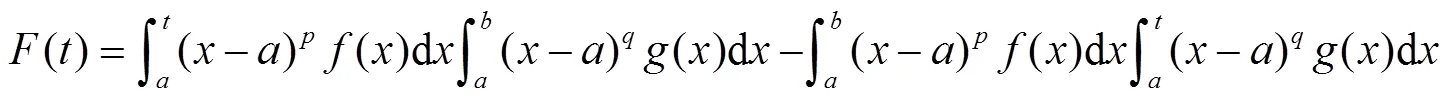
由积分上限函数的求导公式有：

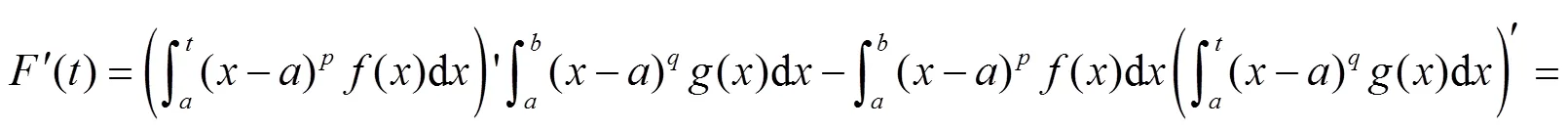
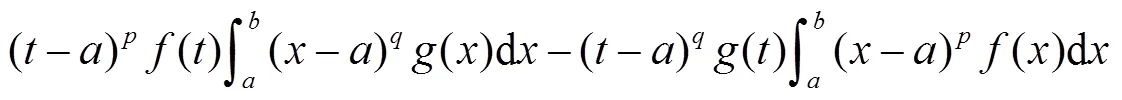
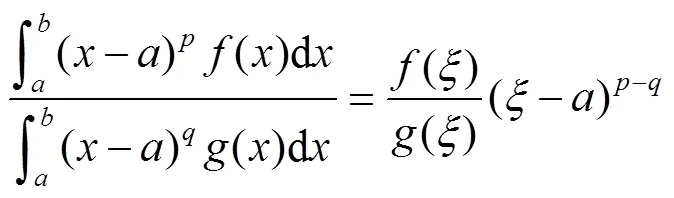
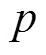
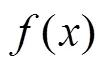
这便是文献[1-2，4]的相关定理.

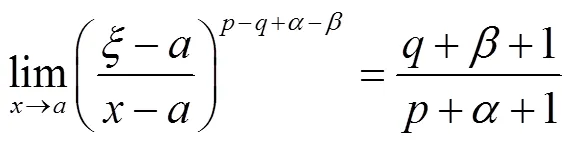
则一方面，由引理1

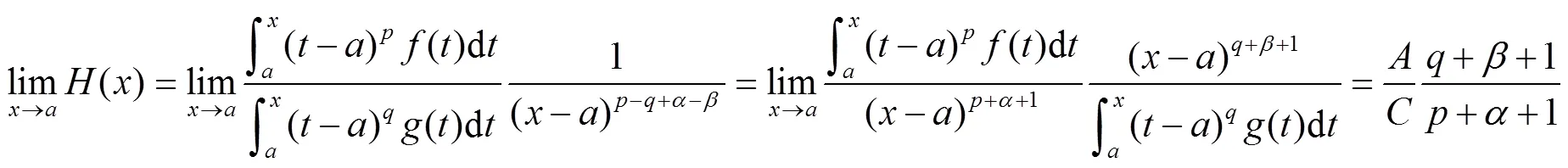
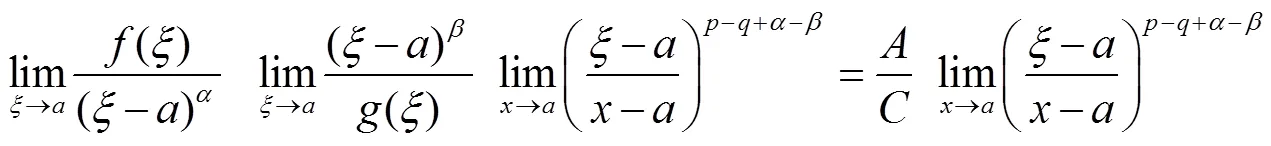
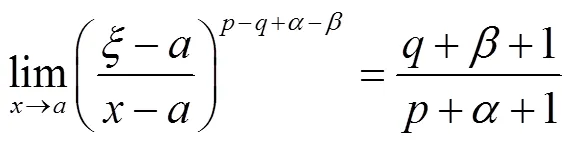
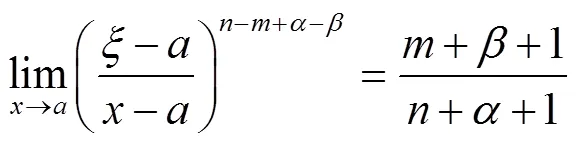
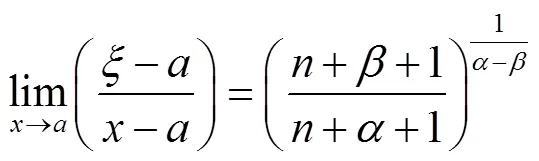
以上定理和推论的结论是具有一般性的结论，可作为微积分中值定理“中间点”渐进性研究成果的补充和推广.

[1] 伍建华，孙霞林，熊德之. 一类积分型中值定理的渐进性讨论[J]. 西南师范大学学报，2012, 37(8): 24-27.

[2] 陈玉. 积分型中值定理的推广及统一表示[J]. 大学数学，2015, 35(2): 61-65.

[3] 杜争光. 广义Cauchy中值定理“中间点”的渐进性[J]. 数学的实践与认识，2015, 45(13): 268-272.

[4] 刘文武，严中权. 积分型Cauchy中值定理中间点的渐进性[J]. 数学的实践与认识，2010, 40(11): 228-231.

[责任编辑：熊玉涛]

A Restudy of a Type of Cauchy’s Mean-Value Theorem of the Integral Type

DUZheng-guang

(Department of Mathematics, Longnan Teachers College, Chengxia 742500, China)

A further study of a type of Cauchy’s mean-value theorem of the integral form revealed a more general conclusion. The asymptotic property of “midpoint” of the theorem was discussed and some results were generalized.

mean-value theorem; midpoint; asymptotic property

1006-7302（2018）02-0015-03

O172.2

A

2017-11-28

国家自然科学基金资助项目（1763040）；陇南市2016年科技指导性计划项目（2016-23）；陇南市2016年科技指导性计划项目（2016-23）

杜争光（1973—），男，甘肃礼县人，副教授，学士，从事数学分析和复变函数研究工作.