评估有无负荷及不同步态下踝关节受力的简化动力学模型

张军, 何旺骁, 金亮, 王丽娟

(1.西安交通大学体育中心, 710049, 西安; 2.西安交通大学生命科学与技术学院, 710049, 西安;3.西安交通大学医学部, 710061, 西安; 4.西安交通大学理学院, 710049, 西安)

在临床医学和体育科学领域,利用非侵入式方法准确确定脚踝作用力的需求在各种诊断与研究中越来越迫切[1]。针对这一需求,已有研究者利用正向动力学和逆动力学这2种基本方法建立了一些模型[2-4],并用于估测踝关节动力学和运动过程中关节的力矩和受力[5]。一些学者利用这些模型研究了运动员[6]和关节炎患者[7]踝关节的受力状态,并得出了令人满意的结果。例如:Kakihana等分析了横向楔形鞋垫对踝关节和距下关节力矩的影响[8];Pain等估测了下落着地时软组织活动对关节力矩和作用力的影响[9]。此外,还有研究者对相关模型进行了改进,进一步提高了模型的精度,并利用复杂的人体三维模型计算了踝关节的受力情况[10]。

然而,到目前为止还没有一个可以系统地描述包括肌肉力量、分段加速度和力矩的下肢踝关节动力学模型,这在一定程度上限制了与踝关节相关的医学诊断和运动受力的研究。因此,本文基于逆动力学方法,结合身体姿态和身体所受外力的测量结果,建立了一个简化动力学下肢模型和相应的动力学方程,用来系统地描述踝关节在不同运动方式和负重情况下的受力。其中,身体姿态采用高速摄像机拍摄固定于受试者四肢的标记物的运动轨迹得到,身体外部受力则由力平台记录[11]。根据相邻肢体上跟踪目标的运动轨迹,计算出各段肢体的相对位置和姿态,从而确定关节角度;通过不同的操作,从这些数据中进一步得到速度和加速度。之后,根据加速度以及身体受到的其他外部作用力预测相应关节的作用力和力矩,再结合肌肉的解剖学数据与身体各部位的生物力学参数,具体计算出关节作用力数据。

先前的许多研究已经证明,不同的足部状态(包括穿着不同种类的鞋和裸足)对于踝关节受力以及运动伤害的预防具有很大的影响[12-13]。利用本文提出的简化下肢动力学模型和相应的动力学方程,可对不同足部状态(穿着运动鞋、穿着登山鞋以及裸足)下踝关节的受力情况进行分析验证,并进一步为挑选合适的鞋类从而防止运动损伤提供依据。

1 人体下肢的简化动力学模型

用二维刚性杆模型来模拟下肢,由测得的身体各部分的重力和足底压力,利用力矩平衡方程来确定关节力矩。在更为精确的分析中,应考虑肌肉和关节的作用力。

在图1所示的模型中:人体的上半身被看作是一个附着在髋关节之上的砝码,腿和脚由二维刚性杆模型模拟,踝关节和髋关节被简化为铰链连接,肌肉作用力分别由小腿两端的未知作用力表示,如图1a、1b所示;作用于脚上的力包括脚的重力Gf、胫前力F1、腓肠肌作用力F2、踝关节作用力Fa和地面反作用力Fg,如图1c所示。

踝关节的受力包括x轴方向的Fa,x和y轴方向的Fa,y。根据牛顿第二定律,性力等于脚部其他力在x轴方向分力的合力,即

脚部在x轴方向的惯

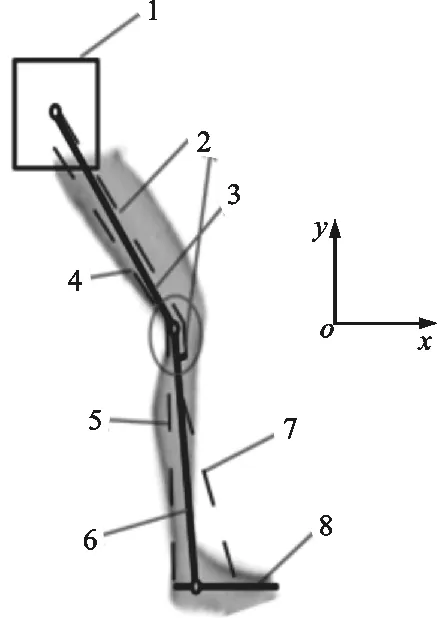
1:身体上半部分;2:股四头肌;3:大腿;4:股二头肌;5:腓肠肌;6:小腿;7:胫骨前肌;8:足部(a)下肢刚性杆模型

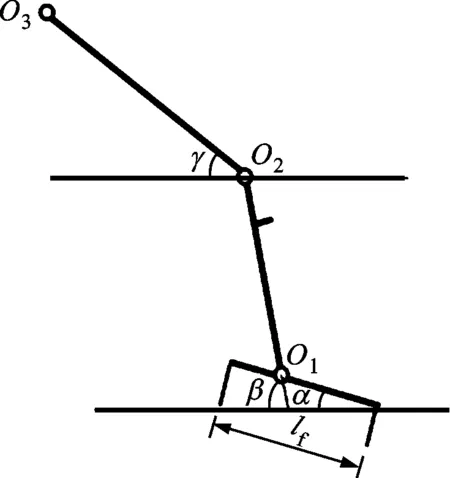
(b)腿足二维刚性杆模型

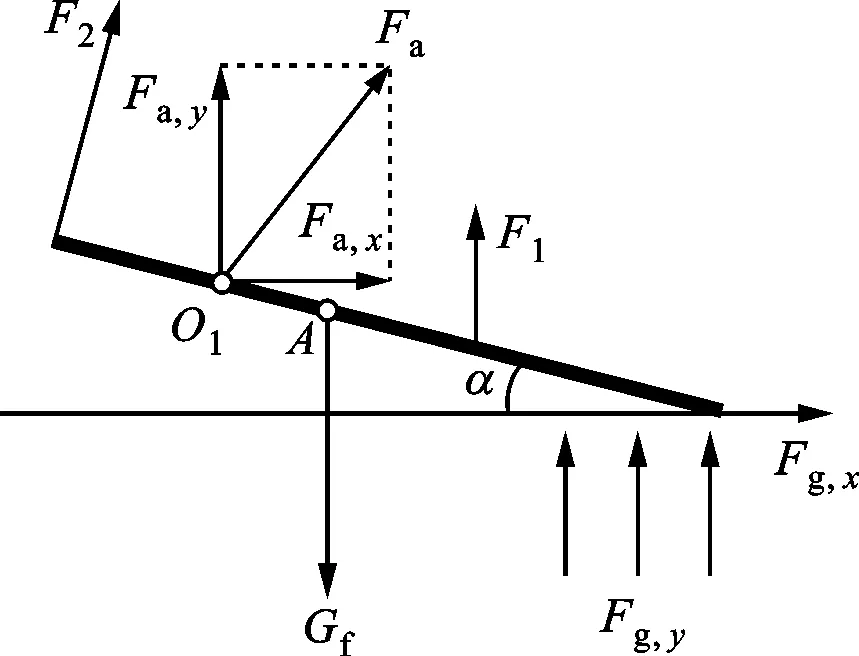
(c)足部受力简图图1 下肢力学模型及受力图解

(1)

式中:xA为A点的x轴坐标;mf为脚部的质量;F1,x、F2,x、Fa,x和Fg,x分别代表胫前力、腓肠肌作用力、踝关节作用力和地面反作用力在x轴方向的分力。同样,y轴方向的运动方程可表示为

(2)

式中:yA为A点的y轴坐标;F1,y、F2,y、Fa,y和Fg,y分别代表胫前力、腓肠肌作用力、踝关节作用力和地面反作用力在y轴方向的分力。值得注意的是,该等式考虑了重力的影响。

根据力矩平衡原理,可以得到如下方程

(3)

式中:Jf为脚部的转动惯量;α为脚部的角度;Ma,x、Ma,y、M2、M1、Mg,x和Mg,y分别代表Fa,x、Fa,y、F2、F1、Fg,x和Fg,y指向质心的力矩。

根据文献[14]中的肌肉解剖数据和几何知识,利用三角函数可将F1和F2分别分解为F1,x、F1,y、F2,x、F2,y的加和形式。由于足底的压力中心在模型中视为做匀速运动,所以地面反作用力在y轴方向的力矩Mg,y可以用Fg,y和t/tt来表示。为统一计算,所有受试者都是由脚部开始接触力平台开始计时,到脚部离开力平台计时结束。为精确求解,总时间tt在下面的例子中均取0.94 s。

2 控制方程

由于三角函数的形式复杂,方程组仍然难以求解,因此有必要利用限制变量变化范围的方法来简化方程。简化后的方程如下

(4)

Fg,x+0.1Fa,y(t)-0.1mfg

(5)

式中:lf为脚的长度。

读了那么多年书，到头来却写不准常见字，如此荒诞的时代病见于很多人。在这个握着鼠标放下笔杆的时代里，键盘上的手指翻飞代替了白纸上的一笔一画；网络上的检索复制代替了头脑中的凝词炼句。而学校里汉字教学日渐缩水，生活中网言网语屡见不鲜，甚至一些字典也干脆“顺乎潮流”“将错就错”……长年累月下来，越来越多的人开始淡忘汉字的具体构造，只识得大体轮廓，遑论对于汉字之美的“上下求索”了。近些年，相关讨论时而出现，如今已经降级到“具字有几横”的水平，令人遗憾。而很多人猛然发现，打字惯了的自己已经忘记了“忘字”本身，恐怕这才是最“细思极恐”的。

通过计算人体的生物力学参数,测量地面对下肢的反作用力和运动学数据,可以由以上的方程确定踝关节的受力。

根据实验数据求解上述控制方程(4)和(5)分为2个步骤:生物力学参数的计算;方程(4)和(5)的数值求解。第一步,确定参数mf、mc、Jf、lf、lc和Jc(下角标f表示脚,c表示质心,这里将脚部的几何中心视为质心);第二步,利用高速摄像机和力平台获得的足部运动学数据,求得控制方程(4)和(5)的数值解。踝关节所受的合力Fa可由以下方程计算得到

(6)

3 实验部分

3.1 实验对象、材料及设备

实验对象是6名从西安体育学院筛选的男性运动员,身体各项参数如下:身高(173.0±4.0) cm;体质量(61.7±4.7) kg;年龄(20.7±0.5)岁;脚长(27.3±0.8) cm。

实验材料:哥伦比亚登山鞋、耐克运动鞋各3双(脚长分别为26.5、27.5、28 cm,故每种鞋选择42、43、44欧码各1双)。

使用CASIO摄像机记录运动学数据,使用力平台(KISTLER 9287C,瑞士)捕获动力学信息。

3.2 实验步骤

实验包括基本数据测量、实验准备工作、热身和不同条件下的测试4个步骤。测试分为站立、行走、跑步和踏步等不同的实验条件,分别持续30和60 min。在站立测试时,首先启动高速摄像机和肌电系统,然后启动力平台(此时激活信号同时传输到其他设备),在受试者右脚向前迈出并站在力平台上的同时记录数据。其他步态下的测试程序和站立时相同,但受试者不是停留在力平台上,而是向相反的方向行走、跑步或踏步。

3.3 运动学和动力学数据的处理

为计算质心的坐标和下肢各部位的倾斜角度,利用动作分析系统(APAS)处理动态数据,处理的步骤包括数字化(在每一轮实验中利用仪器的目标追踪器件标记脚尖、踝关节和髋关节)、滤波(平滑结果)、变换(将点转化为坐标形式)和显示(使用表格输出坐标)。在进一步的处理中,通过反三角函数和生物力学数据,分别得到质心坐标和身体各部分的倾斜角。利用Bioware软件辅以Kistler测力平台,可在Excel中直接实时输出力的数据。肌电信号通过MegaWin软件用均方根方法取得平均值,并以Excel表格的形式输出。

4 实验结果分析

4.1 模型参数的确定

4.2 模型的建立

用3.1节中的人体参数构建踝关节的动力学模型。由图2～图4可见,在走路、跑步和踏步时,该模型模拟的受试者受力曲线和实际经验相似,且曲线趋势与Tang等人利用高性能计算机得到的结果[10]一致。

(a)踝关节所受的分力

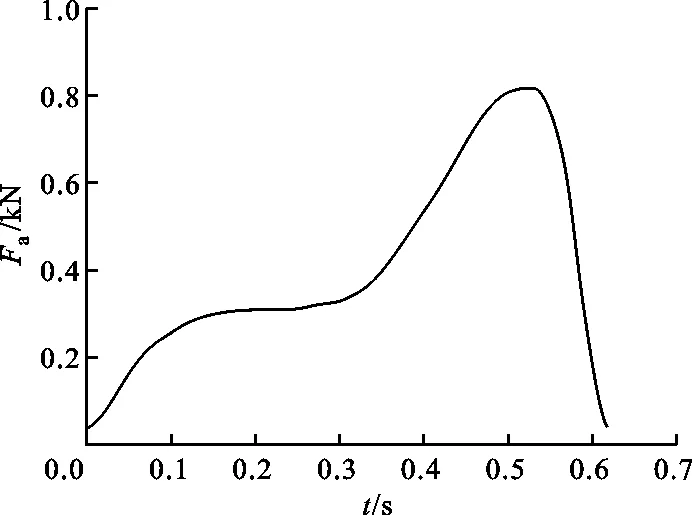
(b)踝关节所受的合力图2 行走过程中踝关节受力的模拟结果

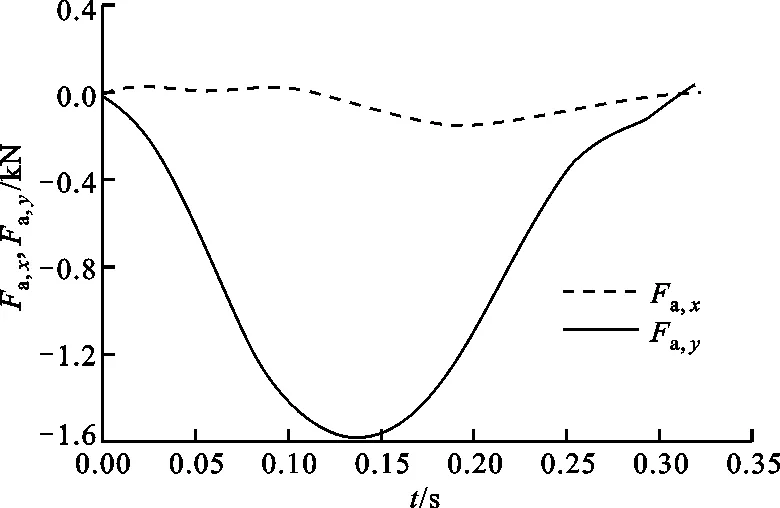
(a)踝关节所受的分力

(b)踝关节所受的合力图3 跑步过程中踝关节受力的模拟结果

(a)踝关节所受的分力

(b)踝关节所受的合力图4 踏步过程中踝关节受力的模拟结果

随后,对无负重、不同步态(行走、跑步和踏步)下5位受试者的踝关节受力进行模拟和分析,得到平均作用力(峰面积除以时间)、峰值力和冲量(曲线对时间进行积分),如图5所示,可见踏步时的平均作用力比跑步时的值高30%,比行走时的值高将近3倍;行走、跑步和踏步的峰值力表现出相同的趋势。此外,不同步态下的冲量几乎相等,说明在3种步态下踝关节的总受力几乎是相同的。

(a)平均作用力

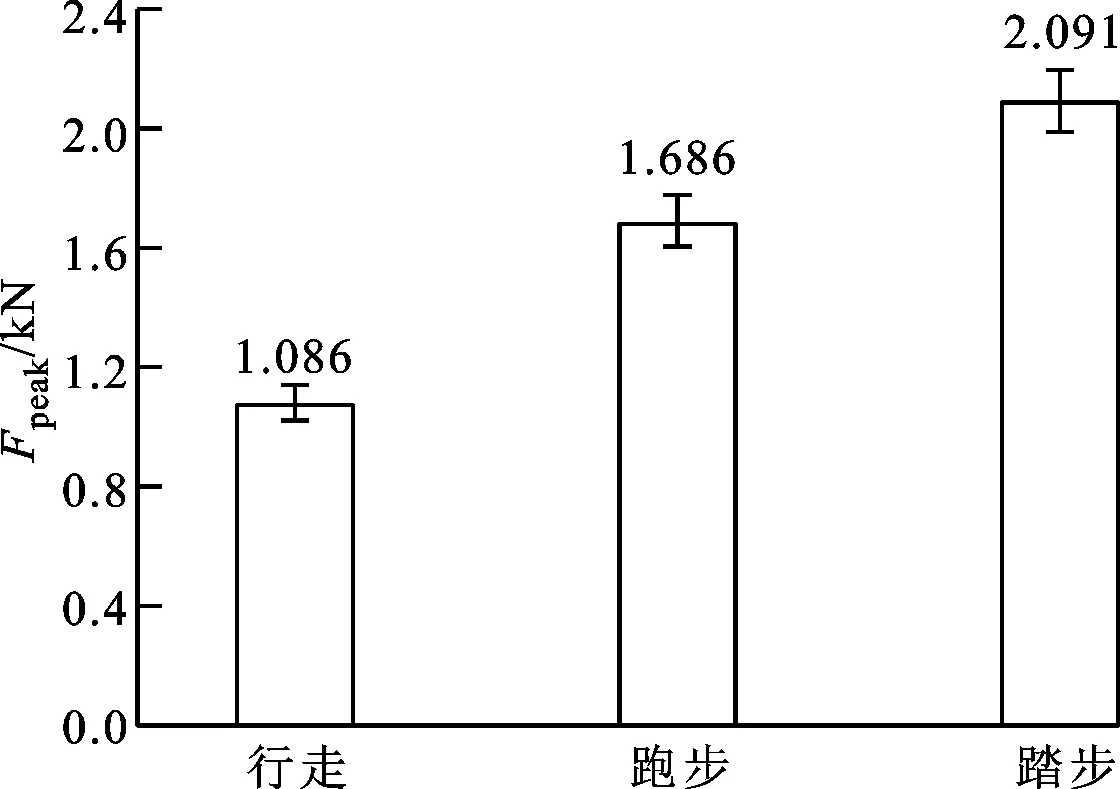
(b)峰值力

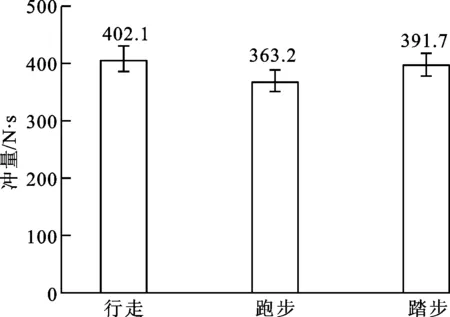
(c)冲量图5 无负重时不同步态下踝关节的平均作用力、峰值力和冲量

采用相同的实验方法,模拟外加10 kg负重后不同步态下踝关节的受力曲线,处理后的数据如图6所示,可见与图5一样,踏步时踝关节的平均受力大于跑步和行走时的平均受力。行走、跑步和踏步的受力峰值也存在相同的趋势。

5 讨 论

5.1 模型的验证

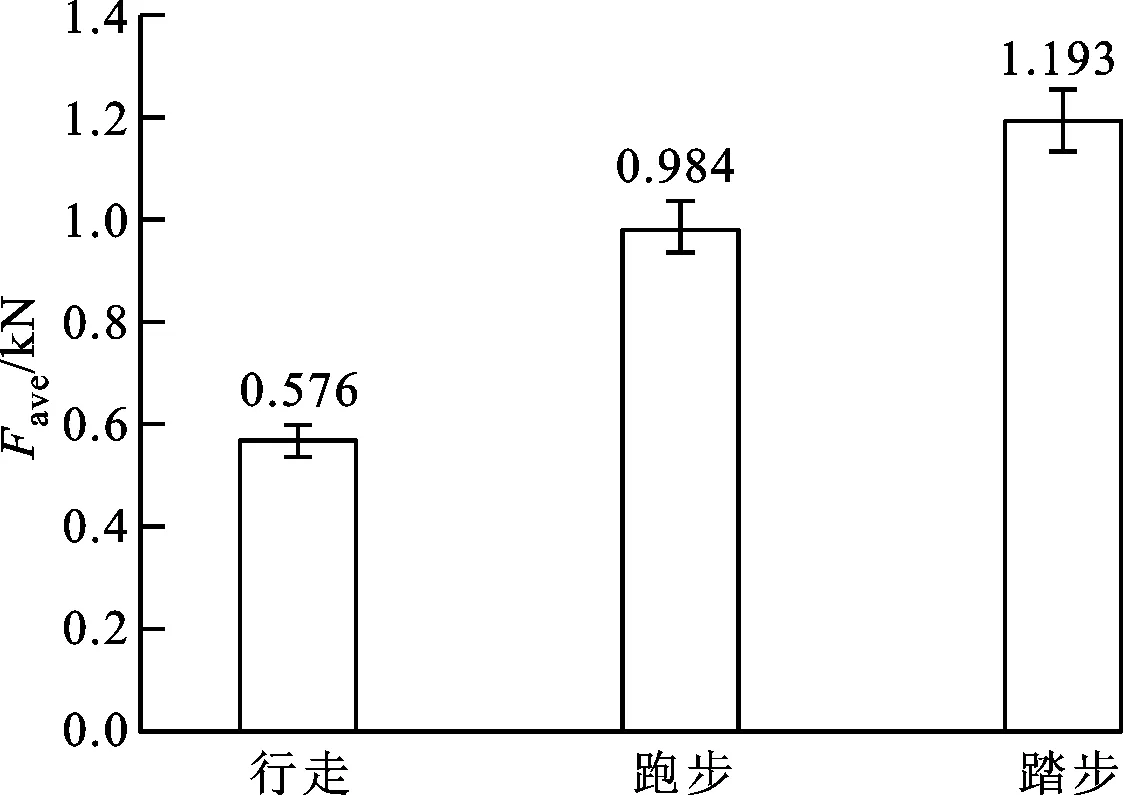
(a)平均作用力

(b)峰值力

(c)冲量图6 负重时不同步态下踝关节的平均作用力、峰值力和冲量

研究结果表明,本文提出的简化动力学模型和其他的复杂模型[1]以及计算机软件的分析模拟[15-16]一样,能够有效预测出踝关节受力。用本文模型获得的肌肉受力曲线与肌电图检测显示的肌电信号曲线具有相似的变化趋势,即在肌肉等长收缩时,肌肉受力随着肌电信号增强而增加,由此表明,本文的简化动力学模型具有较强的合理性和科学性[16]。此外,肌电信号曲线和肌肉受力曲线总是同时达到最大值,这种相似性也在一定程度上进一步验证了本文模型的正确性与合理性。

5.2 生理学解释

将图5、图6所示的平均作用力和峰值力数据除以体质量,可得到平均加速度aave和峰值加速度apeak,结果如图7所示(图中重力加速度g取9.8 m/s2)。由图7可知:行走、跑步和踏步的峰值力具有相同的趋势;相比行走和跑步,踝关节在踏步时受到的作用力更大;踏步时踝关节的峰值力较大,所以踝关节更容易受到伤害,提示在跳跃等动作不能避免的情况下,应当更加注意保护踝关节;在10 kg负重的情况下,跑步时的平均加速度和峰值加速度值大于踏步时的值,提示在负重跑步时应当更加注意踝关节的保护。另外,根据图7很容易发现,行走和跑步时负重会增加踝关节压力(平均加速度和峰值加速度更大),这符合一般的常识。然而,踏步时的相应结果却是相反的,对于这一现象最合理的解释是,10 kg负重条件下被测者的重心明显降低了。

(a)平均加速度

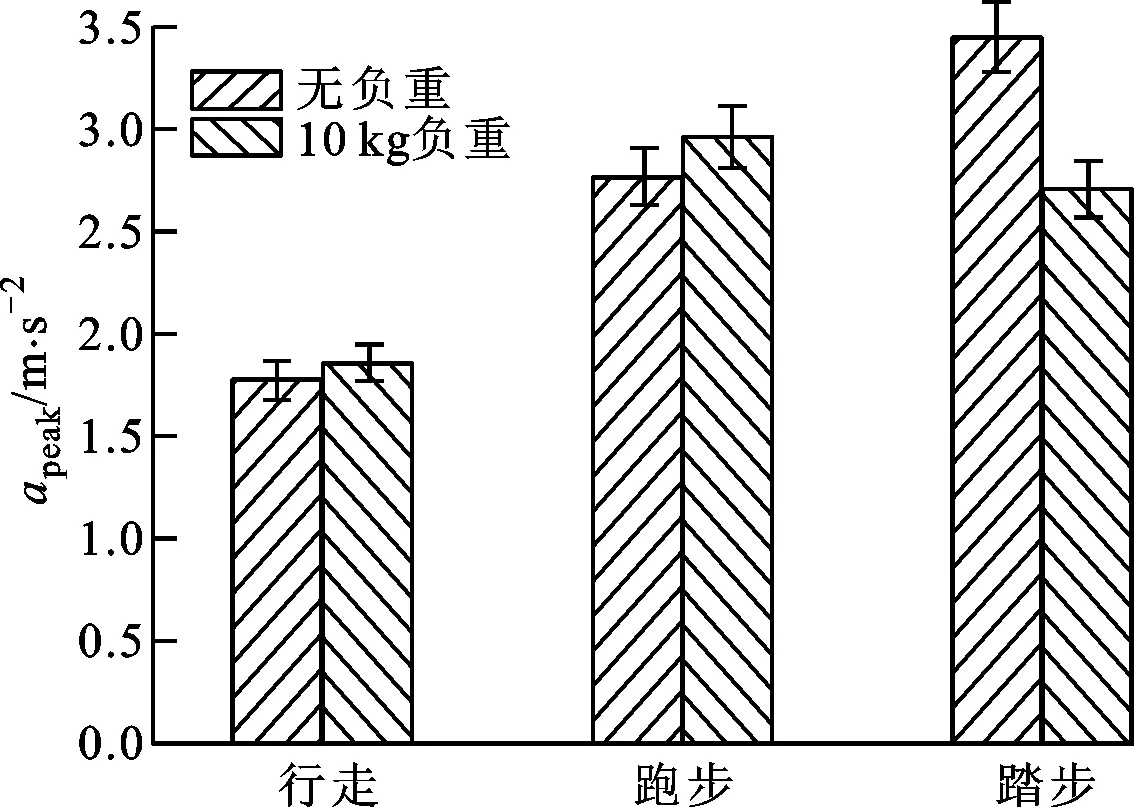
(b)峰值加速度图7 有、无负重时不同步态下踝关节的加速度

本文模型的局限性是暂时无法校正肌肉等长收缩和重心移动带来的计算误差。为了克服这一局限性,可以将个体的模型参数与其导出的个体骨骼参数和肌肉参数相结合,例如借助ISOFIT方法[17],并且可利用测得力的可视化反馈来显著提高受试者被测力的整体精度,以进一步提高实验数据和模型的匹配程度。

5.3 不同鞋类对踝关节受力的影响分析

利用本文的下肢受力模型和相同的试验方法,分别测定在无负重或10 kg负重、不同足部状态(穿着运动鞋、穿着登山鞋或裸足)下踝关节的平均受力情况,实验结果如图8所示。

(a)无负重

(b)负重10 kg图8 有、无负重时不同足部状态在3种步态下的踝关节平均受力情况

与前述实验结果相似,在无负重和负重10 kg的情况下,踏步时的踝关节平均受力均显著高于其他2种步态时的受力,提示应当重点关注踏步时踝关节运动损伤的预防。此外,在踏步时穿着合适的鞋类(如运动鞋,登山鞋等)能够显著分散踝关节受力,从而可有效降低踝关节的运动伤害风险。运动鞋相比登山鞋具有更好的受力分散效果,这可能是由于运动鞋鞋底的缓冲材质比登山鞋鞋底的防滑耐磨材质能更好地吸收、分散踝关节的受力,同时运动鞋高帮的设计能帮助固定脚踝部位免受移位、扭伤等困扰[18]。

6 结束语

本文建立了一个简化的下肢动力学模型,用二维刚性杆模型模拟下肢,踝关节和髋关节被简化为铰链连接,肌肉作用力分别由小腿两端的未知作用力表示,并根据测得的身体各部分重力和足底压力,利用力矩平衡方程来确定关节力矩。针对该模型建立了相应的动力学方程,结合高速摄像机和力平台获得的数据,便捷地得到了较高精度的踝关节受力数据,并使用APAS对数据进行了动态处理。利用该动力学模型,可以评估踝关节的受力情况,评价不同步态(如行走、跑步和踏步等)以及有、无负重时踝关节受力的差别,还可对穿着不同鞋类(如运动鞋、登山鞋)和裸足时的踝关节受力进行对比分析。此项研究可应用于下肢保护器具与鞋类研发中对踝关节受力的评价,并且可为临床上更为复杂的运动行为研究提供参考。

参考文献:

[1] WAGNER H, BOSTRÖM K, RINKE B. Predicting isometric force from muscular activation using a physiologically inspired model [J]. Biomechanics and Modeling in Mechanobiology, 2011, 10(6): 955-961.

[2] JONKERS I, SPAEPEN A, PAPAIOANNOU G, et al. An EMG-based, muscle driven forward simulation of single support phase of gait [J]. Journal of Biomechanics, 2002, 35(5): 609-619.

[3] SETH A, PANDY M G. A neuromusculoskeletal tracking method for estimating individual muscle forces in human movement [J]. Journal of Biomechanics, 2007, 40(2): 356-366.

[4] BUCHANAN T S, LLOYD D G, MANAL K, et al. Neuromusculoskeletal modeling: estimation of muscle forces and joint moments and movements from measurements of neural command [J]. Journal of Applied Biomechanics, 2004, 20(4): 367.

[5] 张军, 李建喜, 夏钰坤, 等. 行走过程中人体下肢受力模型的建立与验证 [J]. 西安交通大学学报, 2015, 49(9): 134-140.

ZHANG Jun, LI Jianxi, XIA Yukun, et al. Establishment and verification of a mechanical model for analyzing the forces acted on lower limb during walking [J]. Journal of Xi’an Jiaotong University, 2015, 49(9): 134-140.

[6] BUCKWALTER J A, LANE N E. Athletics and osteoarthritis [J]. Am J Sport Med, 1997, 25: 873-881.

[7] HURWITZ D, RYALS A R, BLOCK J A, et al. Ankle pain and joint loading in subjects with osteoarthritis of the ankle [J]. J Orthop Res, 2000, 18: 572-579.

[8] KAKIHANA W, AKAI M, NAKAZAWA K, et al. Effects of laterally wedged insoles on ankle and subtalar joint moments [J]. Arch Phys Med Rehab, 2005, 86: 1465-1471.

[9] PAIN M T, CHALLIS J H. The influence of soft tissue movement on ground reaction forces, joint torques and joint reaction forces in drop landings [J]. J Biomech, 2006, 39: 119-124.

[10] TANG G, ZHANG X A, ZHANG L L, et al. A technical method using musculoskeletal model to analyse kinetic properties of muscles during human movement [J]. Computer Methods in Biomechanics and Biomedical Engineering, 2011, 14: 615-620.

[11] ORLIN M N, MCPOIL T G. Plantar pressure assessment [J]. Phys Ther, 2000, 80: 399-409.

[12] 何俊良, 刘宇, 傅维杰, 等. 高低帮篮球鞋对踝关节稳定性及肌肉活动影响的研究 [C]∥第十四届全国运动生物力学学术交流大会论文集. 北京: 中国体育科学学会, 2010: 409-413.

[13] 曲毅. 慢跑鞋鞋底硬度对舒适性及缓冲性能的影响 [D]. 北京: 北京体育大学, 2013.

[14] SCHMITT D. Insights into the evolution of human bipedalism from experimental studies of humans and other primates [J]. Journal of Experimental Biology, 2003, 206(9): 1437-1448.

[15] DELP S L, ANDERSON F C, ARNOLD A S, et al. OpenSim: open-source software to create and analyze kinetic simulations of movement [J]. IEEE Transactions on Biomedical Engineering, 2007, 54(11): 1940-1950.

[16] DELP S L, LOAN J P. A computational framework for simulating and analyzing human and animal movement [J]. Computing in Science & Engineering, 2000, 2(5): 46-55.

[17] WAGNER H, SIEBERT T, ELLERBY DJ, et al. ISOFIT: a model-based method to measure muscle-tendon properties simultaneously [J]. Biomechanics and Modeling in Mechanobiology, 2005, 4(1): 10-19.

[18] 蔡宇辉. 慢跑鞋鞋底缓冲减震功能的对比研究 [D]. 北京: 北京师范大学, 2007.

[本刊相关文献链接]

仲继泽,谢志强,沈渡,等.基于空间分布弹性模量的快速动网格方法[J].2018,52(2):136-139.[doi:10.7652/xjtuxb 201802021]

张胜伦,裴世源,徐华,等.考虑瞬态冲击和弹性变形的滑动轴承特性与动力学响应[J].2018,52(1):100-106.[doi:10.7652/xjtuxb201801015]

申建广,陶涛,梅雪松,等.一种数控滚齿机工作台动态特性建模方法及实验分析[J].2017,51(12):1-7.[doi:10.7652/xjtuxb201712001]

杨芳,陈渭,李培.接触力模型对含间隙铰接副多体系统分析的影响[J].2017,51(11):106-117.[doi:10.7652/xjtuxb2017 11015]

尹贵,张小栋,陈江城,等.下肢康复机器人按需辅助自适应控制方法[J].2017,51(10):39-46.[doi:10.7652/xjtuxb 201710007]

妥吉英,邓兆祥,张河山,等.新型扭转准零刚度的振动角度传感系统[J].2017,51(8):90-95.[doi:10.7652/xjtuxb2017 08015]

李文嘉,王安麟,曹岩,等.面向变矩器设计性能的平面流模型选用方法[J].2017,51(7):78-83.[doi:10.7652/xjtuxb 201707012]