流固耦合作用下航空发动机燃烧室热疲劳研究
张俊红, 戴胡伟, 鲁鑫, 王杰, 马梁, 孙宇博
(1.天津大学内燃机燃烧学国家重点实验室, 300354, 天津; 2.天津大学仁爱学院机械工程系, 301636, 天津;3.中国民航大学天津市民用航空器适航与维修重点实验室, 300300, 天津)
航空发动机燃烧室是航空发动机的关键热端部件,其强度和可靠性对发动机运行安全性有直接的影响。目前针对航空发动机燃烧室的研究主要分为流场研究和疲劳寿命研究。
在流场研究方面,由于民航运行安全规定,难以监测航空发动机工作时燃烧室内流场分布的真实情况。对燃烧室流场的研究大多以仿真为主。王宝官等采用二维紊流模型对有气膜冷却的燃烧室内流场及壁温进行数值分析,得到速度场、壁面温度、辐射通量随进口参数的变化规律[1]。雷雨冰等采用三维紊流模型通过多区耦合法对某环形燃烧室化学反应流场进行数值模拟[2],较全面地反映燃烧室的气流流动、换热、燃烧等现象;刘常春等采用SST(shear-stress transport)湍流模型研究了孔阵排列和偏转角对火焰筒冷却效果的影响[3];Fureby采用大涡模拟的方法对环形燃烧室三维两相流场进行模拟,获得燃烧室内流场分布及温度、压力的波动情况[4]。然而,诸多学者的研究重点大多集中于燃烧室的流动特性,对燃烧室内流体域与结构之间的耦合传热特性及其对燃烧室疲劳可靠性研究较少。
在疲劳寿命研究方面,Barrett等通过实验研究了高温环境下哈氏合金低周疲劳性能[5];Meyer等通过对比试验研究了焊缝对哈氏合金疲劳特性的影响[6];易慧通过对燃烧室施加简化的温度载荷获得燃烧室应力应变,并对燃烧室进行寿命预测[7]。实验研究及对燃烧室基体施加的简化载的荷仿真研究不能准确地反应燃烧室复杂多变的工作环境,寿命预测结果准确性较低。目前,对燃烧室工作过程进行CFD仿真准确获得燃烧室温度及应变载荷,并对燃烧室进行疲劳可靠性研究很少。
本文建立了某航空发动机燃烧室湍流燃烧流固耦合模型,对慢车、起飞、爬升、巡航、下降5种典型工况下燃烧室流场进行了数值模拟,获得了燃烧室的温度分布。在验证流固耦合计算准确性的基础上,基于流场计算结果通过非线性静力学分析获得了燃烧室基体的应力和应变分布。
1 基本物理方程
1.1 流固耦合计算方程
本文采用简化的联合概率密度函数(PDF)模型模拟发动机燃烧过程,非预混燃烧PDF模型的平均混合分数方程及混合分数方差的守恒方程分别为
(1)
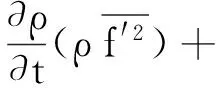
Cgμt(
(2)
(3)

考虑流体与结构之间的相互作用,在作用处边界需满足流体与固体温度、热流量、位移、应力相等,满足以下方程
(4)
式中:T为温度;q为热流量;d为位移;τ为应力;下标f、s分别表示流体、固体。
1.2 非线性静力学分析方程
假定构件温度变化为ΔT,则应力、应变和温度的关系式可表示为
在弹性区域
σ=De(ε-εT)
(5)
在塑性区域
σ=Dep(ε-εT)
(6)
εT=αT
(7)
式中:De为弹性矩阵;Dep为相应的弹塑性矩阵;εT为热应变增量;α为热膨胀列阵。
根据虚位移原理,可建立节点载荷有限元方程的增量表达式
在弹性区域中的单元
(8)
在塑性区域中的单元
(9)
总体载荷
R=∑Re
(10)
基本平衡方程式可写为
Kδ=R
(11)
式中:K为构件刚度矩阵;δ为结构节点位移列向量。
1.3 热疲劳分析方程
在结构疲劳寿命计算中,Manson-Coffin公式和线性损伤理论应用广泛。Manson在独立研究热疲劳问题的过程中提出一种以塑性应变幅为参量的疲劳寿命描述法[8],即
(12)
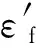
线性累积损伤理论由Miner提出[9],零部件的损伤变量为
(13)
式中:ni为第i段载荷下的循环数;Ni为第i段载荷下结构失效的循环数;k为载荷数。当D为1时,可认为零部件失效,发生疲劳破坏[10]。
2 几何建模和力学性能实验
2.1 几何建模
本文以某航空发动机环形燃烧室为研究对象。该环形燃烧室火焰筒前端沿周向均布20个旋流器,每个旋流器中心有一个双油路离心喷嘴;火焰筒沿周向均布80个主燃孔、120个掺混孔;火焰筒内、外壁分别沿轴向布置4、5道冷却气膜,共10 540个气膜冷却孔。
为得到与燃烧室实体吻合度较高的计算模型,采用HEXAGON公司的ROMER绝对关节臂外接激光型非接触式三坐标扫描仪获取环形燃烧室截面点云数据及整体点云数据。通过对后期坐标数据的逆向处理实现燃烧室实体模型的建立,燃烧室点云数据及三维模型如图1所示。

(a)截面点云数据 (b)整体点云数据 (c)燃烧室三维模型图1 燃烧室点云数据及三维模型
2.2 哈氏合金拉伸试验
燃烧室基体材料为哈氏合金X,为获得哈氏合金X准确力学性能参数,进行拉伸试验。依据GB/T228.1—2010[11]设计矩形截面拉伸试样,尺寸和试验前、后试样如图2所示。试验在INSTRON万能力学试验机上进行,选用4个平行试样依据GB/T228.1—2010规定的方法,通过控制试验机横梁位移速率控制试件的应变速率,横梁位移速率为1 mm/min,通过0.5级全自动轴向引伸计测量试样轴向变形,实验数据采样频率为10 Hz。
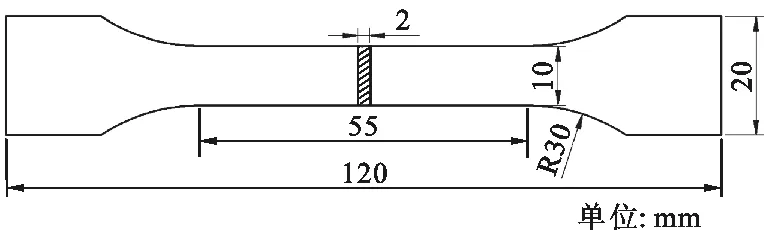
(a)拉伸试验矩形截面试样尺寸

(b)试验前试样

(c)试验后试样图2 哈氏合金X力学性能试验试样
实验测得哈氏合金X弹性模量为278 MPa,屈服强度为463 MPa,抗拉强度为980 MPa。绘制哈氏合金X拉伸试验工程应力-应变曲线,依据GB/T228.1—2010用多项式回归方法对工程应力-应变曲线进行光滑处理,哈氏合金X工程应力-应变曲线如图3所示。
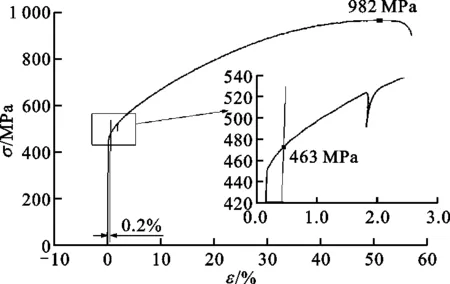
图3 哈氏合金X工程应力-应变曲线
在拉伸试验中,由于试样的横截面积减小,其真实应力比工程应力大,试件的真实应力为
σa=σ(1+ε)
(14)
(15)
式中:ε为试件应变。
3 流固耦合模拟
3.1 数学模型
利用FLUENT系统对典型工况下燃烧室内的湍流燃烧进行模拟,通过编写UDF(user define function)程序实现迭代计算过程中流体域与固体域之间的数据交换,使得流体域与固体域耦合面上的位移、热流量、温度、应力等相等。选用模拟旋流能力强且收敛性较好的Realizablek-ε双方程模型模拟燃烧室内的湍流流动[12],选用P1辐射模型模拟燃烧室内的辐射传热,选用压力雾化喷嘴模型模拟燃油喷射过程,采用随机轨道模型进行两相流计算,用拉格朗日法跟踪离散液滴在流场中的运动和运输,用欧拉法描述气相守恒,通过在气相守恒方程中加入相应的源项来考虑液滴对气相的影响;选用PDF非预混燃烧模型模拟湍流扩散燃烧,通过在能量守恒中加入相应的源项来考虑燃烧对流场的影响,采用SIMPLE算法和二阶迎风格式进行求解。
3.2 网格划分
燃烧室具有以2个旋流器头部为周期的周向周期性结构特征。为减少计算量,选取2个旋流器头部,即1/10扇形段作为计算域,如图4a所示。燃烧室流体计算域形状复杂,为更准确地描述流体域形状,采用变形能力强的四面体网格对流体域进行网格划分,基本网格尺寸大小为5 mm。气膜冷却孔对燃烧室壁面温度分布有极大的影响,其孔径仅有1.5 mm,为保证计算准确性,对气膜冷却孔部分网格进行局部加密,此处网格大小0.3 mm。气膜冷却孔处网格尺寸与其他区域网格尺寸差别较大,为防止尺寸差别过大导致网格畸形引起CFD计算不准确,设定网格尺寸增长率不超过20%。为稳定气流、改善流场计算的收敛性,添加进、出口流道,设置进、出口流道长度为30 mm,以减小进出口边界压力反射对流场计算域的影响。
燃烧室基体为薄壁件,壁厚小于2 mm,其形状对流场影响较大,为更好地反应燃烧室形状对流场的影响,采用基本尺寸为1 mm具有二阶精度四面体单元对燃烧室基体进行网格划分,对燃烧室基体气膜冷却孔、掺混孔孔边等位置网格进行局部加密,网格尺寸0.3 mm。燃烧室基体表面喷涂有一层厚约0.2 mm的热障涂层,热障涂层起隔热作用,可降低燃烧室基体的工作温度[13],本文计算考虑热障涂层的影响,采用基础尺寸0.2 mm的四面体网格对其进行网格划分。对流体域及固体域进行网格划分,获得2 339 390个流体网格单元及2 305 363个固体网格单元,流固耦合计算模型如图4所示。
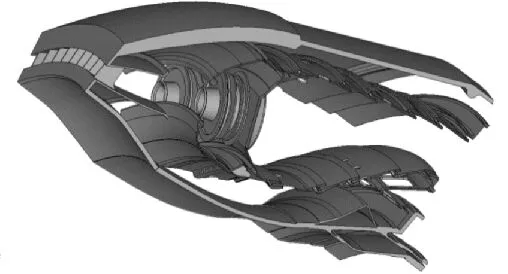
(a)1/10扇形段计算域

(b)流体域网格

(c)固体域网格图4 流固耦合计算模型
3.3 结果分析
本文基于发动机试车数据,将该发动机完整的工作循环简化为慢车、最大、爬升、巡航、下降5个典型工况,各工况进气压力、进气温度、喷油量如表1所示。流场入口采用压力入口边界条件,出口截面采用自由流边界条件,壁面采用无滑移边界条件,通过壁面函数法确定近壁处湍动能k及湍动能耗散率ε,燃烧室两侧面为旋转周期性边界条件,旋转角度为36°。
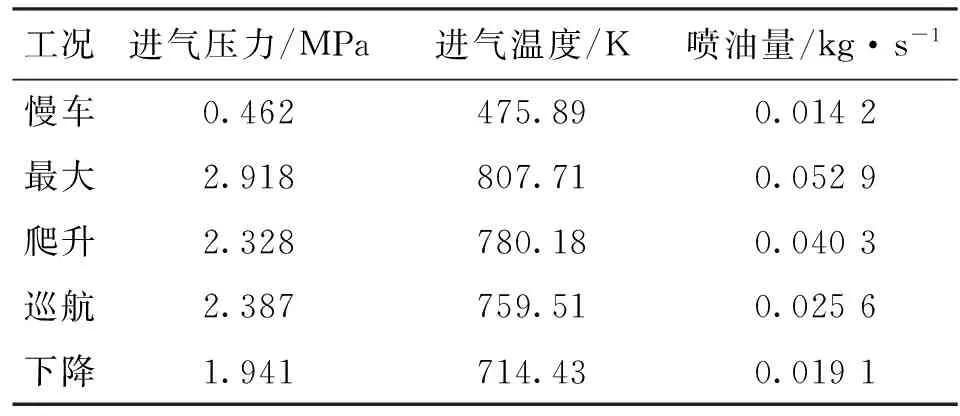
表1 典型工况下发动机运行参数
在热障涂层服役过程中,环境温度高于热障涂层相变温度时,热障涂层会发生相变和烧结[14]随着热障涂层服役时间的增加,不同相变程度的位置宏观样貌会有所不同。为验证流固耦合仿真结果的准确性,将热障涂层外表面温度场与实际服役燃烧室热障涂层宏观样貌进行对比。由于各个工况下热障涂层表面温度值大小有一定差异,但其分布规律相似,选用巡航状态下热障涂层温度场与实际服役燃烧室热障涂层宏观样貌进行对比,如图5所示。

(a)温度场 (b)燃烧室图5 热障涂层温度场与实际服役燃烧室宏观样貌对比
不同工况下燃烧室基体表面温度分布如图6所示,慢车状态、最大状态、爬升状态、巡航状态、下降状态燃烧室基体表面最高温度分别为1 081.60、1 387.39、1 329.93、1 243.26、1 147.82 K,由于燃烧室内环壁掺混孔下游区域靠近辐射高温区,该位置整体温度较高,最高温度点也位于此区域;在掺混孔正下方小部分区域,从掺混孔处进入燃烧室内部的气流对此区域有一定的冷却作用,使得该区域温度较低;在掺混孔下游区域,温度分布不均匀,高温区与低温区最大温差可达237 K(最大状态下),这易使得该区域热应力较大导致疲劳破坏,燃烧室基体实际开裂位置也多位于此处。
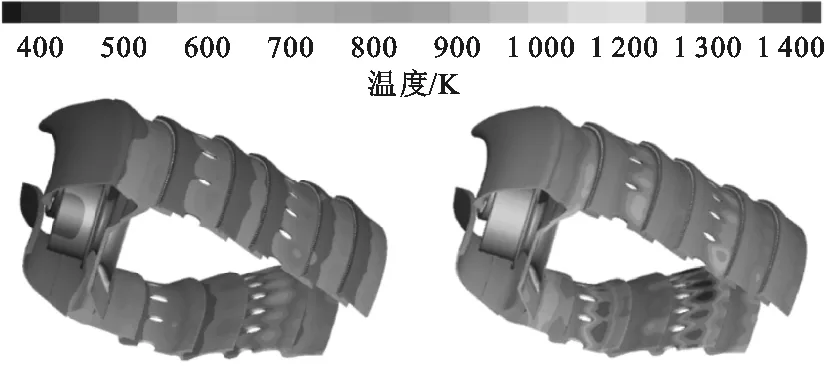
(a)慢车状态 (b)最大状态

(c)爬升状态 (d)巡航状态

(e)下降状态图6 不同工况下燃烧室基体表面温度分布
4 非线性静力学分析
4.1 载荷及边界条件
燃烧室承受冷热气流冲击受热不均匀,各处变形不一致相互约束产生热应力[15]。将流固耦合计算得到的温度作为载荷;将哈氏合金X力学性能拉伸试验结果作为燃烧室基体材料属性;按照燃烧室实际装配情况,约束燃烧室基体底面轴向自由度,约束周期性对称面周向自由度;通过有限单元法对燃烧室基体基本平衡方程进行求解,获得各节点的应变分布。

图7 主燃孔及掺混孔编号
4.2 结果分析
为便于后续分析,对燃烧室基体壁面部分主燃孔掺混孔进行编号,如图7所示。各工况下燃烧室基体塑性变形如图8所示。由图8可知,各工况下燃烧室基体塑性应变主要发生在主燃孔、掺混孔及气膜冷却孔下游区域,随着发动机负荷的增大,燃烧室基体热负荷增加,燃烧室整体塑性变形逐渐增大,燃烧室各工况下最大应变点位置及最大应变如表2所示。

表2 各工况下燃烧室最大应变点位置及最大应变

(a)慢车状态 (b)最大状态

(c)爬升状态 (d)巡航状态

(e)下降状态图8 燃烧室塑性应变
应变较大位置与实际裂纹对比如图9所示,各应变较大位置对应实际服役燃烧室基体位置均出现了不同程度的裂纹;其中,最大状态下及下降状态下,燃烧室基体最大应变位置与实际服役燃烧室基体裂纹位置基本吻合;慢车状态及巡航状态下,燃烧室基体应变最大位置对应实际服役燃烧室基体开裂位置偏差约为1.3 mm、1.5 mm,这是由于慢车状态及巡航状态下,燃烧室基体最大应变位置出现在1号主燃孔及3号主燃孔处,该区域靠近燃烧室喷油嘴,燃油浓度较高,燃烧过程中易形成碳烟,随着航空发动机服役时间的增加,碳烟附着在燃烧室壁面使得该区域局部传热特性发生改变,使得最大应变位置与实际裂纹位置有较小的偏差。总体而言,模拟结果的最大应变位置与燃烧室实际失效位置对应良好,表明有限元计算结果可靠,可作为下一步计算的依据。

(a)慢车状态下1号孔应变 (b)1号孔裂纹

(c)最大状态下2号孔应变 (d)2号孔裂纹

(e)巡航状态下3号孔应变 (f)3号孔裂纹

(g)下降状态下4号孔应变 (h)4号孔裂纹图9 应变较大位置与实际裂纹对比
5 疲劳寿命预测
5.1 危险点的选取及载荷谱的确定
根据应变分析结果及实际服役航空发动机燃烧室基体裂纹分布情况,对1号、3号主燃孔及2号、4号掺混孔4个易失效的位置进行寿命预测。
本文研究对象为某民用飞机上使用的航空发动机,从其飞行记录中摘取飞机发动机19个起落循环的数据,获得其典型工作循环,如图10所示[16]。由于机动状态负荷较小,加速、反推力、减速过程时间很短,这几个阶段对疲劳寿命影响较小,因此忽略这几个阶段的影响,将发动机典型工作循环简化为“慢车—起飞—爬升—巡航—下降—慢车”。
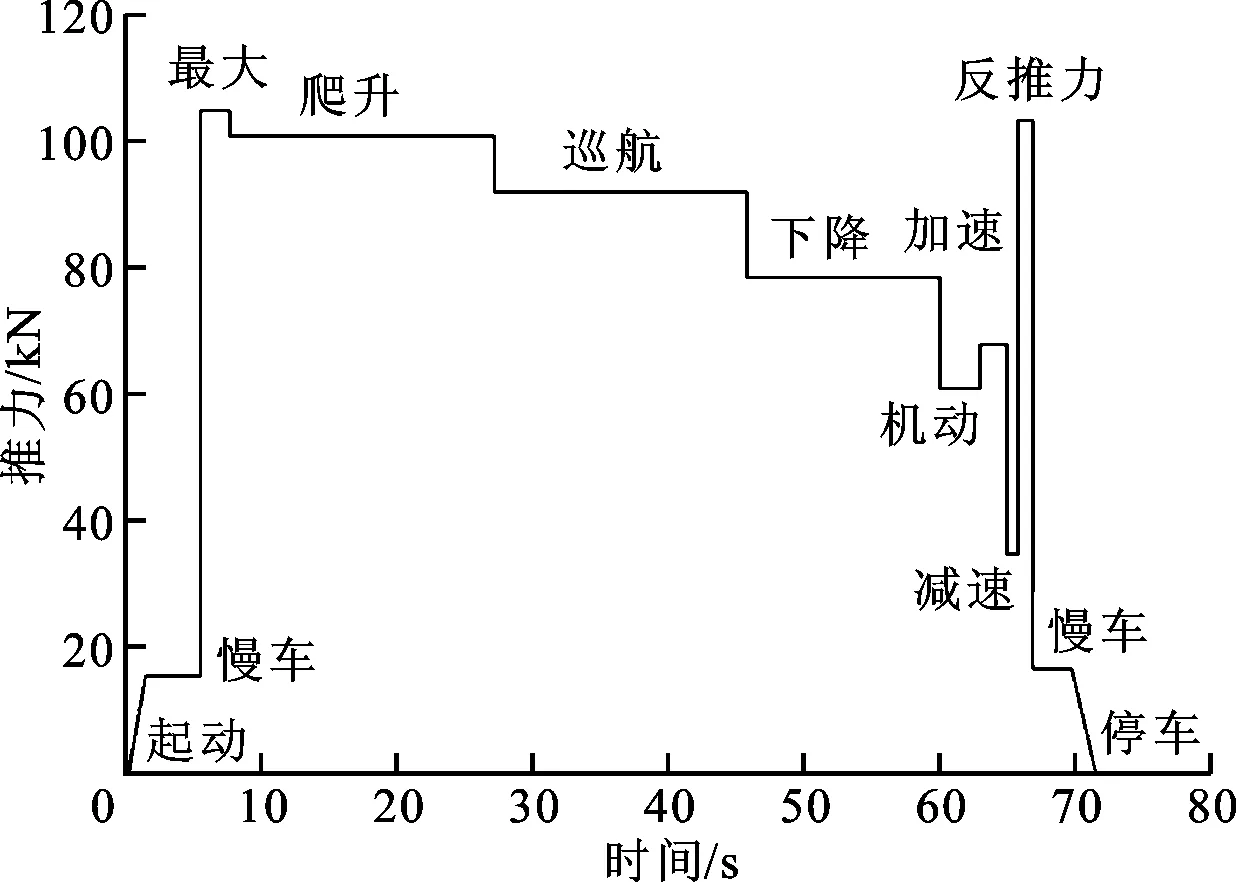
图10 某航空发动机典型工作循环
5.2 危险点疲劳寿命预测
该机型的设计维修手册中要求对燃烧室可靠度的为99.5%,采用文献[17]所述的方法,设定样件存活率99.5%,置信区间95%,对Hong等的试验数据[18]进行拟合,得到873、1 033、1 143 K环境下哈氏合金X的Manson-Coffin公式,分别为
εp1=0.072 6(2Nf)-0.340 87
(16)
εp2=0.051 9(2Nf)-0.351 59
(17)
εp=0.275(2Nf)-0.590 44
(18)
根据流场仿真结果,危险点不同工况下工作温度范围在856~1 191 K之间,分别将不同工况下危险点应变代入上式,求得危险点在873、1033、1 143 K下疲劳寿命,通过Lagrange插值法获得危险点在实际工作温度下疲劳寿命。通过线性累积损伤理论计算得到在典型工作循环下各危险点位置的损伤累积值,当D达到1时,可认为零部件失效,发生疲劳破坏。计算结果表明1号、3号主燃孔及2号、4号掺混孔寿命循环数为13 754、9 381、7 126、11 693。
6 结 论
本文基于流固耦合方法对某航空发动机燃烧室典型工况下流场进行了仿真,获得了不同工况下燃烧室基体温度,通过非线性静力学分析得到了不同工况下燃烧室基体塑性应变分布,对危险点进行了寿命预测,得到以下结论。
(1)通过考虑燃烧室基体及热障涂层的典型工况燃烧室CFD仿真发现,在慢车状态下,燃烧室基体整体温度较低,随着发动机负荷上升,燃烧室基体整体温度逐渐升高。由于靠近燃烧高温区域,燃烧室掺混孔下游大部分区域温度较高;由于掺混气流对基体的冷却作用使得掺混孔下游小部分区域燃烧室基体温度较低,掺混孔下游区域温度分布不均匀。
(2)通过非线性有限元仿真发现,不同工况下燃烧室基体塑性应变分布规律相似,随着发动机负荷的上升,燃烧室基体塑性应变值逐渐增大;塑性应变主要出现于主燃孔及掺混孔下游区域,各工况最大应变位置对应实际服役燃烧室基体位置均有不同程度的裂纹,仿真最大应变位置与实际燃烧室位置偏差小于1.5 mm。
(3)考虑温度的影响,通过Manson-Coffin公式及线性累积损伤理论计算得到在典型工作循环下危险点疲劳寿命,寿命最低点为2号掺混孔处,最低寿命循环数为7 126。
参考文献:
[1] 王宝官, 李永康, 胡正义. 带气膜冷却的火焰筒壁温的数值分析 [J]. 航空学报, 1995, 16(4): 415-421.
WANG Baoguan, LI Yongkang, HU Zhengyi. Numerical analysis of the wall-temperature with film-cooling in the combustion chamber [J]. Acta Aeronautica ET Astronautica Sinica, 1995, 16(4): 415-421.
[2] 雷雨冰, 胡好生, 赵坚行. 环形回流燃烧室两相反应流场的数值研究 [J]. 航空动力学报, 2001, 16(4): 350-354.
LEI Yubing, HU Haosheng, ZHAO Jianxing. Numerical study of two-phase reacting flow in annual reversed combustor [J]. Journal of Aerospace Power, 2001, 16(4): 350-354.
[3] 刘常春, 吉洪湖, 杨芳芳, 等. 孔阵排列和偏转角对多斜孔壁火焰筒冷却效果的影响研究 [J]. 推进技术, 2013, 34(10): 1369-1375.
LIU Changchun, JI Honghu, YANG Fangfang, et al. Numerical study on cooling effects of hole arrangement and deflected angle of inclined multi-hole on annular flame tube [J]. Journal of Propulsion Technology, 2013, 34(10): 1369-1375.
[4] FUREBY C. LES of a multi-burner annular gas turbine combustor [J]. Flow, Turbulence and Combustion, 2010, 84(3): 543-564.
[5] BARRETT P R, AHMED R, MENON M, et al. Isothermal low-cycle fatigue and fatigue-creep of Haynes 230 [J]. International Journal of Solids & Structures, 2016, 88/89: 146-164.
[6] MEYER-OLBERSLEBEN F, KASIK N, ILSCHNER B, et al. The thermal fatigue behavior of the combustor alloys In 617 and HAYNES 230 before and after welding [J]. Metallurgical and Materials Transactions: A, 1999, 30(4): 981-989.
[7] 易慧. 环形燃烧室火焰筒强度寿命技术研究 [D]. 南京: 南京航空航天大学, 2008: 5-6.
[8] MANSON S S. Fatigue: A complex subject some simple approximations [J]. Experimental Mechanics, 1965, 5(7): 193-226.
[9] MINER M A. Cumulative damage in fatigue [J]. Journal of Applied Mechanics, 1945, 12(3): 159-164.
[10] 付曦, 张俊红, 寇海军, 等. 复杂载荷下轴流压气机叶片疲劳损伤数值研究 [J]. 西安交通大学学报, 2017, 51(5): 149-155.
FU Xi, ZHANG Junhong, KOU Haijun, et al. Numerical study on the fatigue damage of compressor blade under complex loads [J]. Journal of Xi’an Jiaotong University, 2017, 51(5): 149-155.
[11] 全国钢标准化技术委员会. 金属材料拉伸试验第1部分: 室温试验方法GB/T228.1—2010 [S]. 北京: 中国标准出版社, 2010.
[12] JONES W P, LAUNDER B E. The prediction of laminarization with a two-equation model of turbulence [J]. International Journal of Heat & Mass Transfer, 1972, 15(2): 301-314.
[13] PADTURE N P, GELL M, JORDAN E H. TBCs for gas-turbine engine applications [J]. Science, 2002, 296(5566): 280-284.
[14] 刘怀菲. 二元稀土氧化物复合稳定氧化锆热障涂层材料的制备及性能研究 [D]. 长沙: 中南大学, 2011: 47-50.
[15] 严宗达, 王洪礼. 热应力 [M]. 北京: 高等教育出版社, 1993: 76-82.
[16] 付娜. 某航空发动机涡轮盘和叶片的强度分析与寿命计算 [D]. 西安: 西北工业大学, 2006: 12-13.
[17] 傅惠民, 刘成瑞.ε-N曲线和P-ε-N曲线整体推断方法 [J]. 航空动力学报, 2006, 21(6): 957-961.
FU Huimin, LIU Chengrui. Integral influence method forε-NandP-ε-Ncurves [J]. Journal of Aerospace Power, 2006, 21(6): 957-961.
[18] HONG H U, KIM I S, CHOI B G, et al. Effects of temperature and strain range on fatigue cracking behavior in hastelloy X [J]. Materials Letters, 2008, 62(28): 4351-4353.
[本刊相关文献链接]
季家东,葛培琪,毕文波,等.采用不同管排组合的换热器弹性管束壳程流体诱导振动响应.2018,52(3):69-75.[doi:10.7652/xjtuxb201803010]
仲继泽,谢志强,沈渡,等.基于虚功原理的流固耦合面力和位移传递方法.2018,52(3):160-167.[doi:10.7652/xjtuxb 201803022]
文键,李科,刘育策,等.利用流固耦合分析的板翅式换热器锯齿型翅片多目标优化.2018,52(2):130-135.[doi:10.7652/xjtuxb201802020]
仲继泽,谢志强,沈渡,等.基于空间分布弹性模量的快速动网格方法.2018,52(2):136-139.[doi:10.7652/xjtuxb2018 02021]
仲继泽,徐自力.流固单向耦合的能量法及机翼颤振预测.2017,51(1):109-114.[doi:10.7652/xjtuxb201701017]
范增华,荣伟彬,王乐锋,等.压电微喷辅助液滴的多物理场耦合与实验.2016,50(11):56-61.[doi:10.7652/xjtuxb2016 11009]
仲继泽,徐自力,陶磊.基于虚拟弹性体的快速动网格方法.2016,50(10):132-138.[doi:10.7652/xjtuxb201610020]
姜涛,黄伟,王安麟.多路阀阀芯节流槽拓扑结构组合的神经网络模型.2016,50(6):36-41.[doi:10.7652/xjtuxb2016 06006]
高炎,晏鑫,李军.燃气透平叶片尾缘开缝结构冷却性能的数值研究.2016,50(3):29-37.[doi:10.7652/xjtuxb201603005]
郭涛,管志成,孙光普,等.调频振子-液体联合水平减振的流固耦合机理研究.2016,50(1):28-33.[doi:10.7652/xjtuxb 201601005]
宋明毅,吴伟烽,李直.汽车空调压缩机气阀运动规律模拟.2015,49(12):144-150.[doi:10.7652/xjtuxb201512023]
季家东,葛培琪,毕文波.换热器内弹性管束流体组合诱导振动响应的数值分析.2015,49(9):24-29.[doi:10.7652/xjtuxb201509005]
曹文瑾,孙中国,席光.系泊型浮体运动的无网格法数值模型.2015,49(3):62-66.[doi:10.7652/xjtuxb201503011]

