基于灰度信息度量的阵发性房颤自动检测方法

张瑞, 王继斌

(西北大学医学大数据研究中心, 710127, 西安)

心房颤动(简称房颤)是一种较为常见的心律失常疾病[1],按照发作时长可以分为阵发性、持续性、和永久性房颤。由于阵发性房颤的发作具有偶发性及持续时间短等特点,因此临床上经常会出现难以捕捉到发作信号而造成漏诊的现象,进而威胁患者的健康与生命。基于此,实现阵发性房颤发作的及时检测与识别,具有极为重要的临床意义和现实意义[2]。心电图(ECG)是临床最常用的检查工具之一,主要用于记录人体心脏的放电行为。房颤发作时心电图通常表现出两大特征:RR间期绝对不规则;P波缺失,而代之以连续、快速、不规则的房颤波(也称f波)。传统的房颤诊断主要由专业医师通过视觉观察心电图来完成,但是通过对长时程心电图的视觉检测来发现房颤波是一个非常耗时的过程,而且非常依赖于医师的个人经验。因此,开展阵发性房颤自动检测的研究已成为近年来的热点问题[3]。

目前,对阵发性房颤自动检测的研究主要是从刻画心电图的RR间期绝对不规则和P波缺失两方面出发。基于RR间期的阵发性房颤检测算法主要涉及小波变换、统计模型、庞加莱散点图等方法[4-5];基于P波缺失的阵发性房颤检测算法主要有P波变异分析法、TQ间隔法、小波包分析等[6-8]。本文提出一种基于灰度信息度量的阵发性房颤自动检测方法。将所提取的融合特征结合超限学习机[9],最终完成阵发性房颤的自动检测。

1 方 法

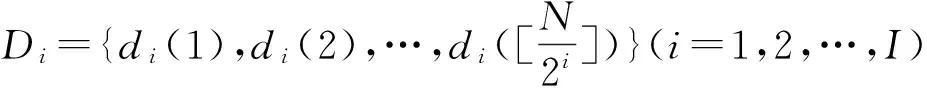
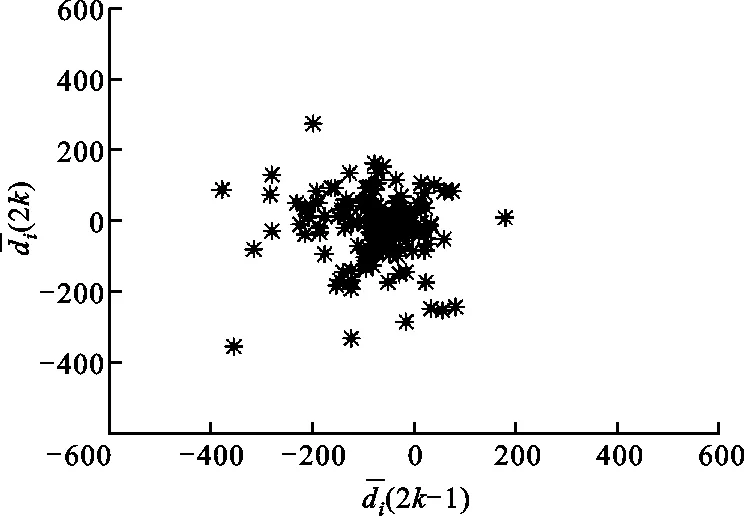
图1 心电信号小波分解系数的一阶差分散点图

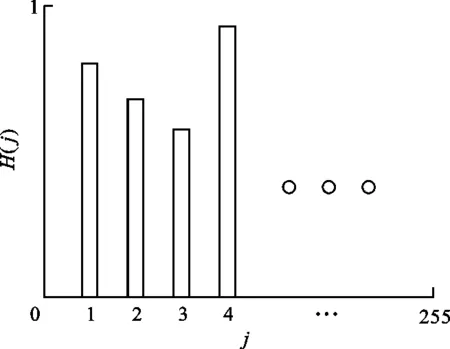
图2 心电信号小波分解系数的灰度直方图

由于差分图中的散点呈现出不同程度的重合分布,重合的点越多,亮度越深,单位像素的灰度值越小。在此基础上,本文采用方差、变异系数、香农熵来刻画灰度直方图的分布情况,分别定义为

(1)

(2)

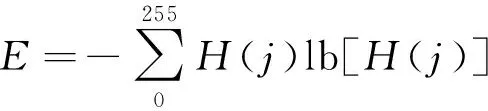
(3)

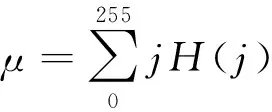
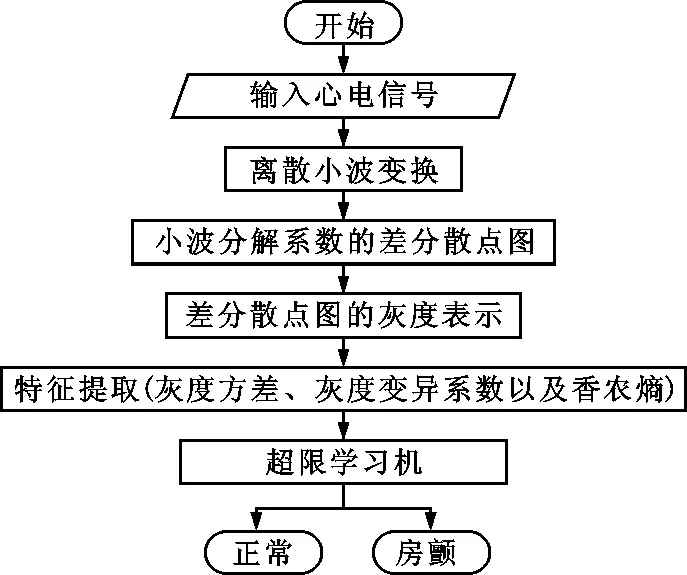
图3 基于灰度信息度量的阵发性房颤自动检测算法流程

2 数值实验结果与分析

2.1 心电数据

本文实验采用MIT-BIH心房颤动数据库[17]的数值,该数据库由美国麻省理工学院(MIT)与波士顿贝丝以色列医院(BIH)合作建立,是世界上样本量最大的心电数据库,包含心房颤动、心律失常、ST段改变、噪声测试等不同数据集。本文采用心房颤动数据集进行数值实验,该数据集包含23个阵发性房颤心电片段,每个片段时长为10 h,采样频率为250 Hz,采样带宽为0.1～40 Hz,采样精度为12 bit。“记录04043”中两段时长5 s的正常心电片段和房颤心电片段如图4所示。本文所有数值实验均在i73.9 GHz CPU和12 GB RAM,以及MATLAB 8.1.0的环境下运行。

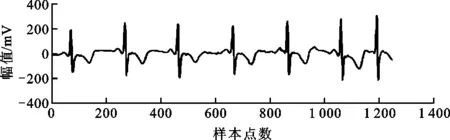
(a)窦性心律

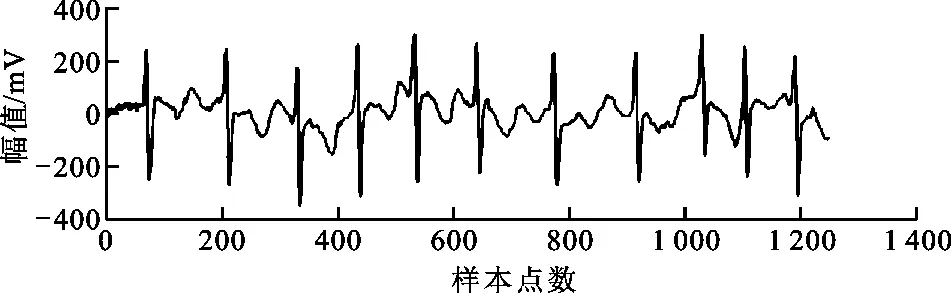
(b)房颤图4 “记录04043”心电片段

2.2 实验结果与分析

由于P波(或f波)所处的信号频带范围均在2～12 Hz内,因而结合采样率,DWT中的分解层数设置为4,母小波为db4函数。图4中所示两个心电片段所对应的小波分解系数和所对应的一阶差分散点图与灰度直方图如图5～7所示。由图6可知,正常窦性心律的散点分布比较集中,而房颤发作时散点分布相对比较分散。这是由于房颤发作时,心房失去规律的伸缩功能,心房活动变得紊乱,心电图表现出一系列连续、快速、不规则的心房颤动波。由图7可知,正常窦性心律的灰度值变化范围为0～30,主要集中于20之前;当房颤发作时,灰度值变化范围扩展为0～50,且大多都集中于30之前。由此可知,患者在房颤发作时,灰度级的变化范围要比未发作时大一些,这从另一个层面反映出患者心房电活动的无序性。

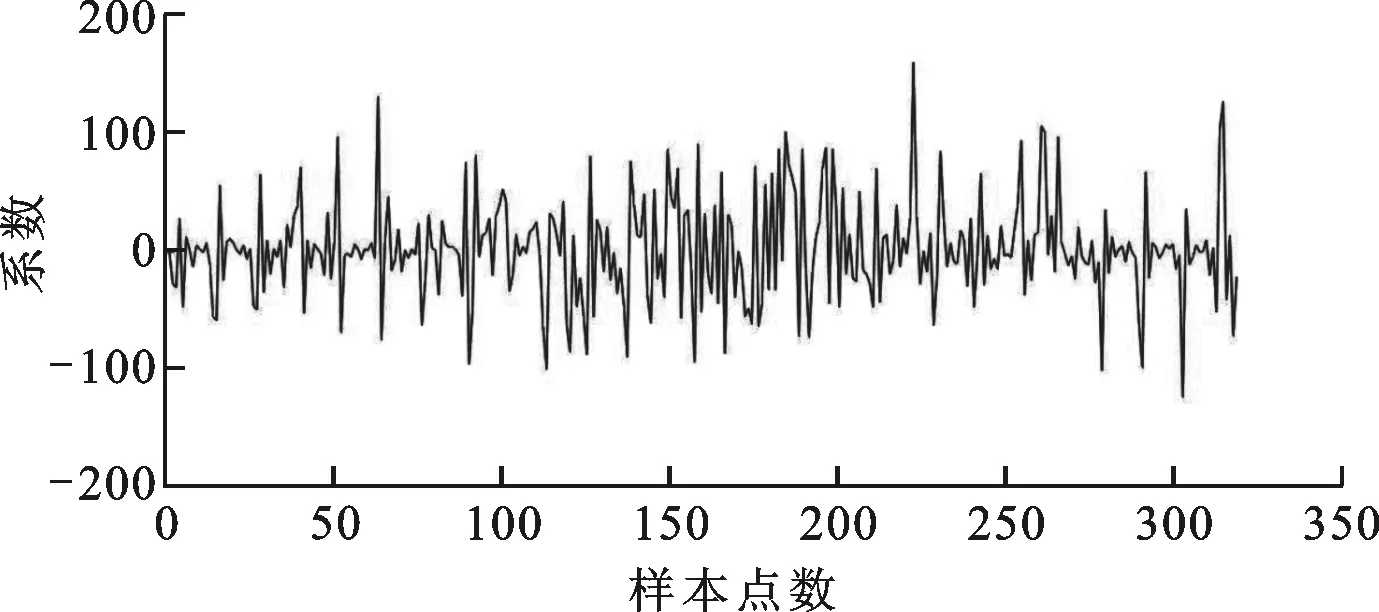
(a)窦性心律

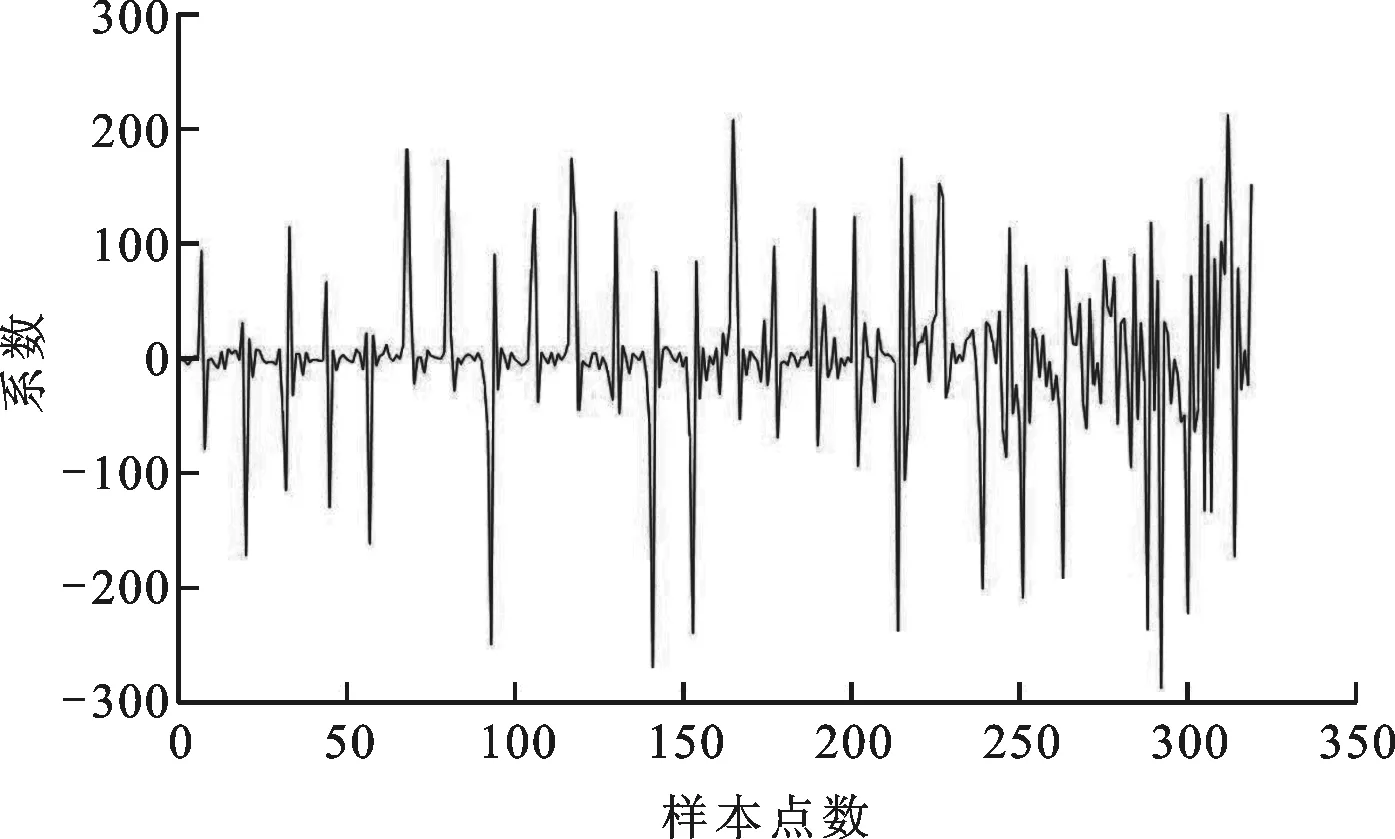
(b)房颤图5 “记录04043”心电片段的第4层小波分解系数

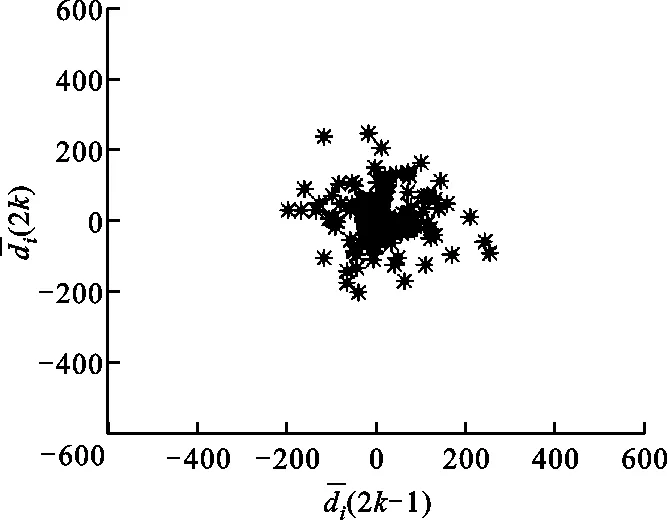
(a)窦性心律

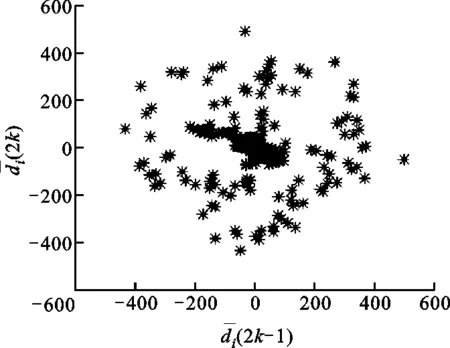
(b)房颤图6 “记录04043”心电片段的一阶差分散点图

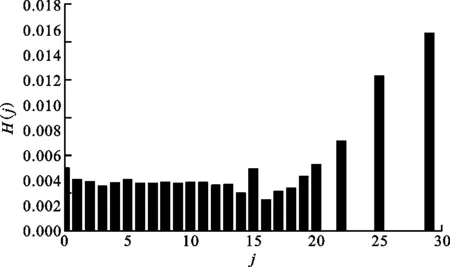
(a)窦性心律

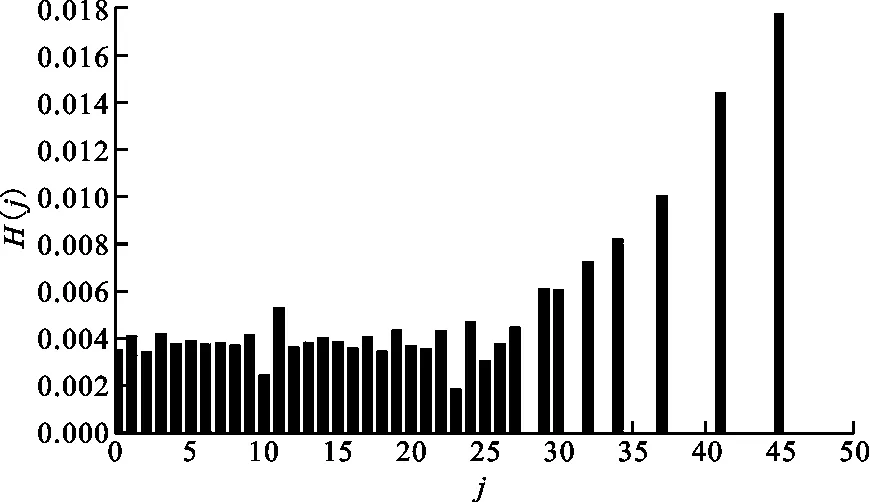
(b)房颤图7 “记录04043”心电片段的灰度直方图

本文采用超限学习机完成最后的分类,通过交叉验证法确定其最优隐节点个数为15。文中采用准确率A、敏感度S以及特异度P作为性能评价指标,它们的计算公式为

(4)

(5)

(6)

式中:TP为真阳性,表示房颤心电被正确检测为房颤心电;FN为假阴性,表示房颤心电被误检测为正常心电;TN为真阴性,表示正常心电被正确检测为正常心电;FP为假阳性,表示正常心电被误检测为房颤心电。

数值实验中,首先从23个心电记录中随机选取7个时长为2 h的心电记录,其次将这些心电信号进行无重叠分段处理,每个心电片段长度为8 s(2 000个采样点),所有数据被随机均分为训练集和测试集。为了降低随机均分所导致的训练集和测试集中不同类数据点的不均衡,本文将这种随机均分的实验执行50次,并取50次实验的平均结果作为最终分类性能的度量。

表1、表2分别展示了采用本文所提方法对7条心电记录实现阵发性房颤自动检测的性能,表1是个人独立检验的实验结果,表2是6倍交叉检验的实验结果。由表1可知,个人独立检验的各项性能指标均取得较好的实验结果,从而验证了本文所提算法的有效性。由表2可知,本文所提算法在交叉检验中也具有良好的检测效果,进一步说明本文算法能够在临床应用中有效实现阵发性房颤的自动检测。对比表1、表2的实验结果发现,交叉检验的实验结果略低于个人独立检验的实验结果,这主要是由不同患者间的个体差异所造成。

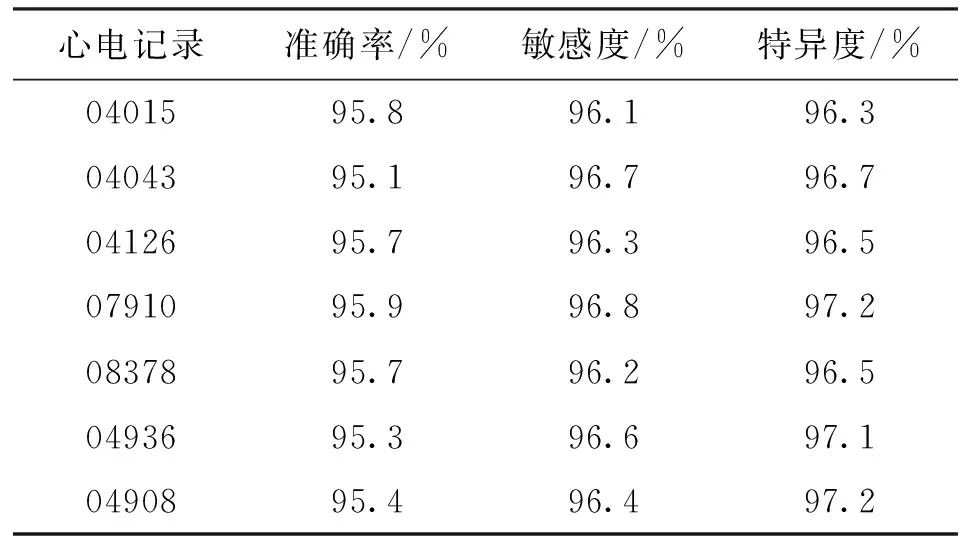
表1 基于灰度信息度量的阵发性房颤自动

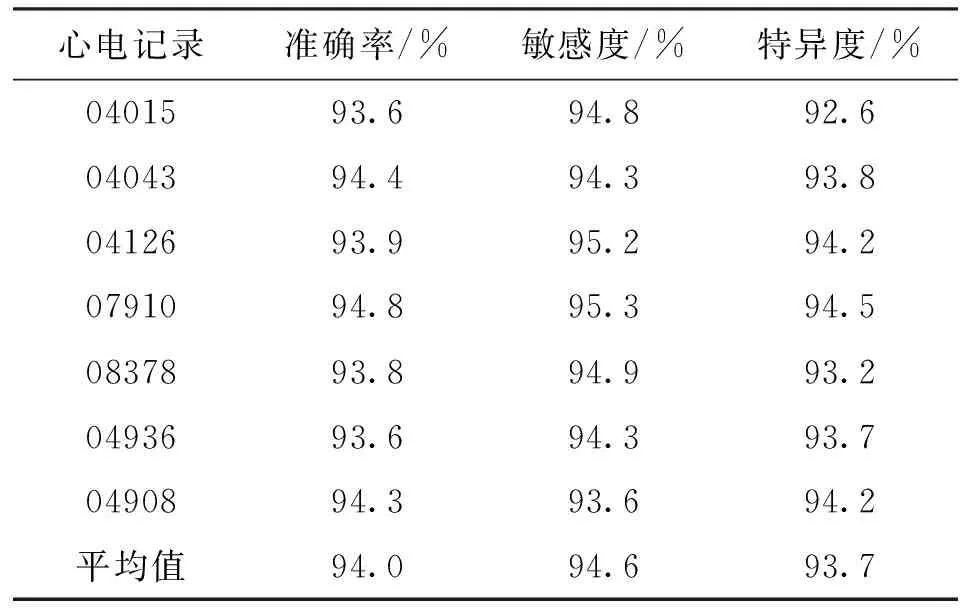
表2 基于灰度信息度量的阵发性房颤自动

3 结 论

本文提出了一种基于灰度信息度量的阵发性房颤自动检测方法。首先,利用离散小波变换对原始心电信号进行分解;其次,选择恰当频率子带信号并对其小波系数进行差分运算,进而得到一阶中心差分散点图以及对应的灰度直方图;然后,分别计算灰度方差、灰度变异系数以及香农熵,作为房颤心电的融合特征;最后,将所提取的融合特征结合超限学习机,完成阵发性房颤的自动检测。采用MIT-BIH心房颤动数据集验证本文所提方法的可行性与有效性。数值实验结果表明,本文所提出的基于灰度信息度量的阵发性房颤自动检测方法具有较高的性能,能较好地完成阵发性房颤的自动检测,其准确率、敏感度、特异度分别平均可达94.0%、94.6%、93.7%。

参考文献:

[1] ZHOU Z, HU D. An epidemiological study on the prevalence of atrial fibrillation in the Chinese population of mainland China [J]. Journal of Epidemiology, 2008, 18(5): 209-216.

[2] 王志敬. 心房颤动的复律探析 [J]. 中华现代内科学杂志, 2008, 5(5): 419-421.

WANG Zhijing. The cardioversion of atrial fibrillation [J]. Chinese Journal of Internal Medicine, 2008, 5(5): 419-421.

[3] 陈灏珠. 心房颤动诊断与治疗的进展和展望 [J]. 中国实用内科杂志, 2006, 26(2): 82-85.

CHEN Haozhu. Diagnosis and treatment of atrial fibrillation progress and prospects [J]. Chinese Journal of Practical Internal Medicine, 2006, 26(2): 8-85.

[4] DASH S, CHON K H, LU S, et al. Automatic real time detection of atrial fibrillation [J]. Annals of Biomedical Engineering, 2009, 37(9): 1701-1709.

[5] PARK J, LEE S, JEON M. Atrial fibrillation detection by heart rate variability in Poincare plot [J]. Biomedical Engineering Online, 2009, 8(1): 38.

[6] ANDRIKOPOULOS G K, DILAVERI-S P E, RICHTRE D J, et al. Increased variance of P wave duration on the electrocardiogram distinguishes patients with idiopathic paroxysmal atrial fibrillation [J]. Pacing & Clinical Electrophysiology Pace, 2000, 23(7): 1127-1132.

[7] DU X, RAO N, QIAN M, et al. A novel method for real-time atrial fibrillation detection in electrocardiograms using multiple parameters [J]. Annals of Noninvasive Electrocardiology, 2014, 19(3): 217-225.

[8] 白鹏飞, 王利, 易子川, 等. 一种心电图P波提取算法 [J]. 中国医学物理学杂志, 2013, 30(2): 4032-4035.

BAI Pengfei, WANG Li, YI Zichuan, et al. A kind of P wave extraction algorithm of electrocardiogram [J]. Chinese Journal of Medical Physics, 2013, 30(2): 4032-4035.

[9] HUANG G B, ZHU Q Y, SIEW C K. Extreme le-arning machine: theory and applications [J]. Neurocomputing, 2006, 70(1): 489-501.

[10] 陈彬强, 张周锁, 郭婷, 等. 双树复小波时频构造在齿轮系装配间隙检测的应用 [J]. 西安交通大学学报, 2013, 47(3): 7-12.

CHEN Binqiang, ZHANG Zhousuo, GUO Ting, et al. Application of double-tree complex wavelet time-frequency structure in the gap detection of gear train assembly [J]. Journal of Xi’an Jiaotong University, 2013, 47(3): 7-12.

[11] 冉启文. 小波变换与分数傅里叶变换理论及应用 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2001.

[12] 刘新颜, 柳稼航, 延军平. 一种基于直方图变换的光学遥感影像自动增强方法 [J]. 西北大学学报(自然科学版), 2016, 46(3): 448-452.

LIU Xinyan, LLU Jiahang, YAN Junping, et al. A method of optical remote sensing image automatic enhancement based on histogram transformation [J]. Journal of Northwest University(Natural Science Edition), 2016, 46(3): 448-452.

[13] 晏春莉, 耿国华, 周明全. 图像数据库中基于颜色的特征提取和度量算法 [J]. 西北大学学报(自然科学版), 2000, 30(3): 189-192.

YAN Chunli, GENG Guohua, ZHOU Mingquan. Color-based feature extraction and metrics algorithm in image database [J]. Journal of Northwest University(Natural Science Edition), 2000, 30(3): 189-192.

[14] 张恒博, 欧宗瑛. 一种基于色彩和灰度直方图的图像检索方法 [J]. 计算机工程, 2004, 30(10): 20-22.

ZHANG Hengbo, OU Zongying. An image retrieval method based on histogram and color histogram [J]. Computer Engineering, 2004, 30(10): 20-22.

[15] 王文森. 变异系数: 一个衡量离散程度简单而有用的统计指标 [J]. 中国统计, 2007, 2007(6): 41-42.

WANG Wensen. Coefficient of variation: a simple and useful statistical indicator to measure dispersion [J]. Chinese Statistics, 2007, 2007(6): 41-42.

[16] 颜若愚, 郑庆华. 使用交叉熵检测和分类网络异常流量 [J]. 西安交通大学学报, 2010, 44(6): 10-15.

YAN Ruoyu, ZHENG Qinghua. Using cross-entropy to detect and classify network abnormal traffic [J]. Journal of Xi’an Jiaotong University, 2010, 44(6): 10-15.

[17] GOLDBERGER A, ARAI L A N. Physio bank, physio toolkit and physio net: components of a new research for complex physiologic signals [J]. Circulation, 2000, 101(23): 215-220.