一种对异常值鲁棒新颖的无格点谱估计方法
张誉馨,张建秋
(复旦大学 电子工程系 智慧网络与系统研究中心,上海 200433)
线谱估计在雷达、声呐、地震学等领域有着广泛的应用,因此它一直是信号处理领域中研究的重要问题[1].经典谱估计算法包括周期图法、非线性最小二乘法(Nonlinear Least Squares, NLS)及多重信号分类法(Multiple Signal Classification, MUSIC)等算法.但这些算法都有各自的限制和缺陷[2].
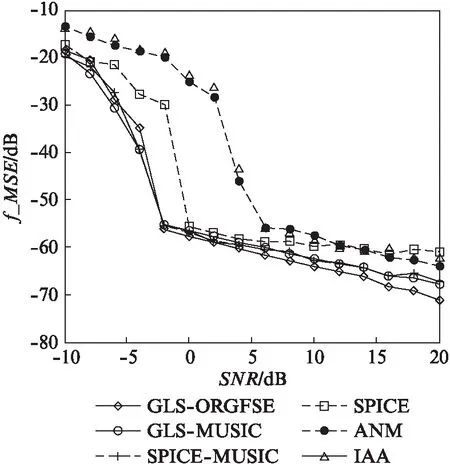
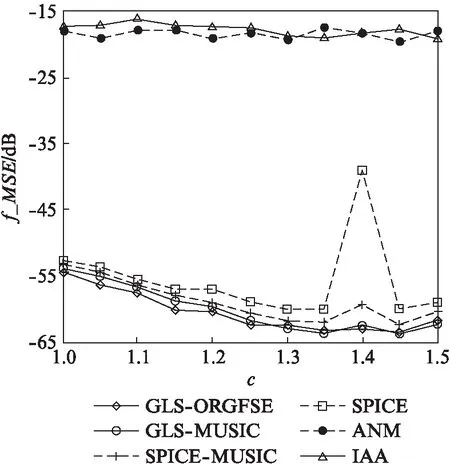
近年来,随着稀疏表示和压缩感知理论[3]的发展,稀疏谱估计算法[4-5]得到了广泛关注.稀疏谱估计算法将连续的频谱离散化为均匀分布的频率格点,并假设待估计谱信号的真实频率分量均落在预先离散化的格点上.这样,对谱信号的频率和幅度的估计,就转化成了求解稀疏支撑向量及其对应的系数.稀疏恢复算法通常假设观测噪声是高斯的.但是,在一些应用场景中,由突发干扰、仪器突然失常或测量者操作不当等因素而导致的观测异常值,使得观测噪声不再能用高斯噪声作为其模型[6].异常值的存在,往往意味着观测数据具有重尾分布[7].文献[7]的研究表明: 重尾数据与高斯数据相比,其产生与均值差异较大的观测值可能性较大.当观测存在异常值时,传统稀疏恢复算法性能将下降甚至失效[8].文献[8]研究表明,使用lp(0 可是,待估计的频率未必落在预先离散化的格点上,此时稀疏谱估计的性能会下降甚至失效,文献[10]称此问题为格点失配问题.近年来,研究者针对格点失配问题展开了广泛的研究,提出一系列无格点稀疏谱估计算法.此类算法可直接求解连续频域的谱,因而有效避免了格点失配问题.原子范数最小化(Atomic Norm Minimization, ANM)[10]和基于协方差的无格点稀疏迭代估计(Gridless SPICE, GLS)算法[12]就是它们的典型代表.然而,ANM算法对观测噪声中可能存在的异常值是不鲁棒的.GLS算法虽然对冲激噪声鲁棒,但是存在频率分裂问题[12].频率分裂意味着对一个幅度较大的待估计线频,算法将在其两侧估计得到两个幅度较小的线频.为了解决GLS算法的频率分裂问题,文献[12]进一步提出了一个谱估计方法,该方法首先使用GLS算法,来估计待估计信号的协方差矩阵,然后采用统计方法[13]来估计模型的阶,最后再使用MUSIC算法来进行频率估计.尽管上述无格点稀疏算法完全消除了频域离散化方法存在的问题,然而它们始终需要待估计线频之间具有足够的间隔才能保证精确恢复.文献[14]的超分辨率谱估计的理论分析表明: 无格点稀疏谱估计算法,只对线频间隔大于2倍采样数据窗主瓣宽度(以后将简称主瓣宽度)以上信号才能精确恢复.文献[15]的研究则表明: 上述线频间隔仅为充分条件,实际的限制则与主瓣宽度和模型阶有关. 为了提高线频间隔位于c倍主瓣宽度内的谱估计精度,本文提出了一种对异常值鲁棒的无格点谱估计(Outlier Robust and Grid Free Spectral Estimation, ORGFSE)算法.该算法首先将GLS算法的频率估计误差描述成误差向量,再利用l1范数对异常值的鲁棒性,来分别约束信号幅度和误差向量的拟合误差,进而通过交替迭代来使它们同时到达最小,以便同时对信号幅度和误差向量的联合鲁棒进行估计.分析表明: 提出的算法在保证收敛的同时,还能提高在c倍主瓣宽度内的谱估计精度.仿真实验结果则在验证分析结果有效性的同时,也表明当信号的实际频率间隔大于1倍主瓣宽度时,大多数情况下,由GLS得出的结果是准确的,只有在极少数情况下(概率通常小于3%),GLS算法才可能出现频率分裂.因此,对于GLS算法估计出的信号,当其线频间距在1倍至c倍主瓣宽度之间时,可利用本文的联合鲁棒估计来进行线谱估计;而一旦发现其间距小于1倍主瓣宽度时,则采用MUSIC算法来进行线谱估计.这样本文提出的算法就能在提高谱估计精度和对重尾分布噪声鲁棒的同时,减小算法的运算量. 本文中的数学符号遵照如下规定: 大写斜黑体字母表示矩阵,小写斜黑体字母表示向量.矩阵diag(x)表示对角线元素为x的对角线矩阵.矩阵T(x)表示向量x的Toeplitz阵.tr(R)表示矩阵R的迹.xi表示向量x的第i个元素.‖x‖p(p≥1)表示向量x的p范数.表示取模. 在线谱估计问题中,观测信号是含噪声的K个复正弦信号的线性组合[1],它可描述为: (1) 定义频率导向矢量a(w)=[e-jw,e-j2w,…,e-jMw]T,则模型式(1)可以重写为如下矩阵形式: (2) (3) (4) 文献[14]和[15]研究表明: 尽管GLS算法不存在格点失配问题,但当实际信号频率位于c(1 (5) (6) 结合式(2)和式(6)可得一个新的观测模型如下: (7) 针对GLS频率估计误差和观测异常值同时存在的稀疏信号恢复问题,本文将优化问题的目标函数描述成如下形式: (8) 由于式(8)所示的目标函数存在两个未知量s和δ,难以直接求解其全局最优解.可是,当求解待恢复信号的幅度矢量s时,如果假设误差矢量δ已知,此时式(8)可转化为: (9) 同理,当求解误差矢量δ时,如果假设待恢复信号的幅度矢量s已知,那么式(8)可重写为: (10) (11) (12) 本文称在利用GLS算法估计值的基础上,再由式(11)和(12)构成的交替迭代谱估计算法,为对异常值鲁棒的无格点谱估计(ORGFSE)算法.由文献[16]的分析可知,本文提出算法ORGFSE的运算复杂度为O(KM2),而MUSIC算法[17]的运算复杂度为O(M3),由于K≪M,因而本文提出算法的运算复杂度更低. 此外,当信号的实际频率间隔大于1倍主瓣宽度时,大多数情况下,由GLS得出的结果是准确的,只有在极少数情况下(概率通常小于3%),GLS算法才可能出现频率分裂.因此,为了减小算法的运算量,本文在GLS谱估计方法的基础上提出了一种对异常值鲁棒新颖的无格点谱估计算法,其算法流程总结如下: 1) 采用GLS算法估计信号的频率及协方差矩阵; 2) 采用统计方法估计模型阶K,即线谱的个数; 3) 对于GLS算法估计出的K个线频,若其中任意两个之间的线频间距在c(1 本文提出算法在文献[18]中称为循环最小算法.由于文献[18]证明了循环最小算法与最大最小算法等价,因此只需证明本文提出算法中,所构造目标函数的替代函数满足文献[18]中定理1所示的上界特性,便可以由文献[18]的结果,直接断定本文提出算法是收敛的. 定理1[18]上界特性: 在点xt处,最大最小算法构造了目标函数f(x)的一个连续的替代函数g(·|xt).此替代函数满足如下的上界特性: g(x|xt)≥f(x)+ct, ∀x, 其中ct=g(xt|xt)-f(xt),进而x可以通过迭代算法更新如下: 在本文算法中,可以将问题式(7)描述为: 本文目的是通过交替迭代算法,来使关于s和δ的函数同时达到最小,以实现了目标函数f(s)的最小化.也就是说,(s,δ)可以通过迭代算法更新如下: 现在,证明本文构造目标函数f(s)的替代函数满足上界特性. g(s,δ*(s(k)))≥g(s,δ*(s))=f(s), 其中c(k)=g(s(k)|s(k))-f(s(k))=g(s(k),δ*(s(k)))-f(s(k))=0.此外,由于 在仿真中,采样点数M为50,信号包含实际线频数K为3,IAA,SPICE算法的频域离散化格点数为500,迭代次数为15次.定义ORGFSE算法中的第k次迭代的残差为: r(k)=y-(A+Bdiag(δ(k)))s(k). 算法中含异常值的观测噪声e分别使用高斯混合模型(Gaussian Mixture Model, GMM)噪声和α-稳定噪声来作为其模型. GMM噪声的概率密度函数为: 其中SNR为信噪比. 对称α-稳定噪声的特征函数为 φ(en)=exp(γα|en|α), 其中参数α称为特征参数,α∈(0,2],仿真中取α=1.4;分散系数γ由SNR和信号功率决定: 本文进行了6组仿真实验.第1,3,5组分别研究算法恢复精度与GMM、α-稳定噪声和高斯噪声及其信噪比的关系.实验中信号的3个线频频率分别在各自的区间内随机分布,且f1∈[0.102,0.104],f2=f1+Δf,f3∈[0.499,0.501],其中Δf=c/M.3个线频的幅度分别为2,2,1.第2,4,6组实验分别研究了3种噪声背景下算法恢复精度与频率间距Δf的关系,实验中3个线频的幅度在区间[1,2]内随机分布. 第1组仿真实验,研究了频率估计误差与α-稳定噪声和信噪比的关系.α-稳定噪声的信噪比范围为0dB 到30dB.仿真中取c=1.1.图1为信号的频率估计误差f_MSE随着α-稳定噪声信噪比增加而变化的仿真结果.仿真实验表明,随着α-稳定噪声信噪比的增加,所有算法的频率估计误差呈现减小的趋势.当信噪比小于8dB时,所有算法均存在较大的频率估计误差.当信噪比大于8dB时,本文提出算法的频率估计误差最小.此外,SPICE算法将频域离散化,存在格点失配问题.当信噪比为10dB以上时,SPICE的估计误差基本不随信噪比增大而变化,此时的误差主要是格点失配误差.由于以上算法均采用l1范数约束拟合误差,因而对α-稳定噪声鲁棒IAA, ANM算法的估计性能较差,原因是这两种算法对α-稳定噪声非常敏感.实验表明,由于采用l1范数约束拟合误差,本文提出算法对α-稳定噪声具有鲁棒性,而且在所有算法中恢复精度最高.当f_MSE为-65dB时,与GLS-MUSIC和SPICE-MUSIC算法相比,本文算法获得了5dB的增益. 图1 频率估计误差与α-稳定噪声和信噪比的关系Fig.1 Frequency estimation error analysis with α-stable noise SNR varying 图2 α-稳定噪声下频率估计误差与频率间距的关系Fig.2 Frequency estimation error analysis with frequency intervals varying under α-stable noise 第2组仿真实验研究了信噪比为20dB的α-稳定噪声背景下频率估计误差与频率间距的关系.图2为信号的频率估计误差f_MSE随着频率间距Δf=c/M的系数c增加而变化的仿真结果.仿真实验表明,随着c的增加,对异常值鲁棒的所有算法的频率估计误差均呈现减小的趋势.当c小于1.4时,本文提出算法的频率估计误差最小.当c大于1.4时,这3种算法的频率估计误差基本相同.此外,在c大于1.2时,SPICE算法的估计误差基本不随信噪比增大而变化,此时的误差主要是格点失配误差;由于IAA和ANM算法对α-稳定噪声非常敏感,因而估计性能较差.仿真实验表明,在α-稳定噪声背景下,当信号存在频率间距c倍主瓣宽度以内的线频时,本文提出算法在所有算法中恢复精度最高.当f_MSE为-65dB时,与GLS-MUSIC和SPICE-MUSIC算法相比,本文算法可分辨的频率间距系数c缩小了0.06. 第5组仿真实验,研究了频率估计误差与高斯噪声和信噪比的关系.高斯噪声信噪比的范围为-5dB到25dB.仿真中取c=1.1.图5(看98页)为信号的频率估计误差f_MSE随着高斯噪声信噪比增加而变化的仿真结果.仿真实验表明,随着高斯噪声信噪比的增加,所有算法的频率估计误差呈现减小的趋势.当信噪比小于0dB时,所有算法均存在较大的频率估计误差.当信噪比大于0dB时,本文提出算法的频率估计误差最小.当信噪比大于2dB时,IAA和SPICE算法的估计误差基本不随信噪比增大而变化,此时的误差主要是格点失配误差.本文仿真实验表明,即使在高斯噪声背景下,本文提出算法也是恢复精度最高.当f_MSE为-65dB时,与ANM,GLS-MUSIC和SPICE-MUSIC算法相比,本文算法获得了6dB的增益. 图3 频率估计误差与GMM噪声及信噪比的关系Fig.3 Frequency estimation error analysis with GMM noise SNR varying 图4 GMM噪声下频率估计误差与频率间距的关系Fig.4 Frequency estimation error analysis with frequency intervals varying under GMM noise 第6组仿真实验研究了信噪比为15dB的高斯噪声背景下频率估计误差与频率间距的关系.图6为信号的频率估计误差f_MSE随着频率间距Δf=c/M的系数c增加而变化的仿真结果.仿真实验表明,随着c的增加,所有算法的频率估计误差呈现减小的趋势.当c小于1.4时,本文算法的恢复精度在所有基于l1范数的算法中仍是最高.当c大于1.4时,这3种算法的频率估计误差基本相同.此外,当c大于1.15时,SPICE和IAA算法的估计误差基本不随信噪比增大而变化,此时的误差主要是格点失配误差.仿真实验表明,在高斯噪声背景下,当信号存在频率间距c倍主瓣宽度以内的线频时,本文提出算法在所有算法中恢复精度最高.当f_MSE为-60dB时,与GLS-MUSIC和SPICE-MUSIC算法相比,本文算法可分辨的频率间距系数c缩小了0.08. 图5 频率估计误差与高斯噪声及信噪比的关系Fig.5 Frequency estimation error analysis with Gaussian noise SNR varying 图6 高斯噪声背景下频率估计误差与频率间距的关系Fig.6 Frequency estimation error analysis with frequency intervals varying under Gaussian noise 本文针对稀疏谱估计中,GLS算法对频率间隔位于c(1 参考文献: [1] LI H. Spectral analysis of signals [J].IEEESignalProcessingMagazine, 2007,24(1): 148-150. [2] YARDIBI T, LI J, STOICA P, et al. Source localization and sensing: Anonparametric iterative adaptive approach based on weighted least squares [J].IEEETAeroElecSys, 2010,46(1): 425-443. [3] WANG Y H, ZHANG J Q. Robust signal recovery algorithm for structured perturbation compressive sensing [J].JournalofSystemsEngineeringandElectronics, 2016,27(02): 319-325. [4] DUARTE M F, BARANIU KR G. Spectral compressive sensing [J].ApplComputHarmonicAnal, 2013,35(1): 111-129. [5] STOICA P, BABU P, LI J. SPICE: A sparse covariance-based estimation method for array processing [J].IEEETransactionsonSignalProcessing, 2011,59(2): 629-638. [6] BEN-HAIM Z, ELDAR Y C, ELAD M. Coherence-based performance guarantees for estimating a sparse vector under random noise [J].IEEETransactionsonSignalProcessing, 2010,58(10): 5030-5043. [7] MIDDLETON D. Non-Gaussian noise models in signal processing for telecommunications: New methods and results for class A and class B noise models [J].IEEETransactionsonInformationTheory, 1999,45(4): 1129-1149. [8] ZENG W J, SO H C, JIANG X. Outlier-robust greedy pursuit algorithms inlp-space for sparse approximation [J].IEEETransactionsonSignalProcessing, 2016,64(1): 60-75. [9] ROJAS C R, KATSELIS D,HJALMARSSON H. A note on the SPICE method [J].IEEETransactionsonSignalProcessing, 2013,61(18): 4545-4551. [10] TANG G, BHASKAR B N, SHAH P,et al. Compressed sensing off the grid [J].IEEETransactionsonInformationTheory, 2013,59(11): 7465-7490. [11] BHASKAR B N, TANG G, RECHT B. Atomic norm denoising with applications to line spectral estimation [J].IEEETransactionsonSignalProcessing, 2013,61(23): 5987-5999. [12] YANG Z, XIE L. On gridless sparse methods for line spectral estimation from complete and incomplete data [J].IEEETransactionsonSignalProcessing, 2015,63(12): 3139-3153. [13] HAN K, NEHORAI A. Improved source number detection and direction estimation with nested arrays and ULAs using jackknifing [J].IEEETransactionsonSignalProcessing, 2013,61(23): 6118-6128. [15] YANG Z, XIE L. Exact joint sparse frequency recovery via optimization methods [J].IEEETransactionsonSignalProcessing, 2016,64(19): 5145-5157. [16] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers [J].Foundations&TrendsinMachineLearning, 2011,3(1): 1-122. [17] SCHMIDT R. Multiple emitter location and signal parameter estimation [J].IEEETransactionsAntennPropag, 1986,34(3): 276-280. [18] SUN Y, BABU P, PALOMAR D. Majorization-Minimization algorithms in signal processing, communications, and machine learning [J].IEEETransactionsonSignalProcessing, 2017,65(3): 794-816.1 信号模型


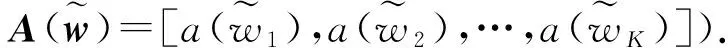
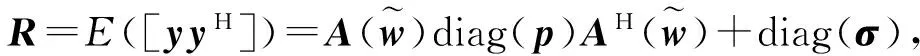
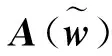
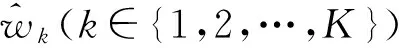
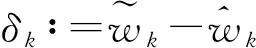
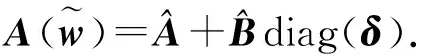

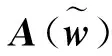
2 算法描述
3 收敛性分析



4 仿真实验与分析
4.1 实验条件


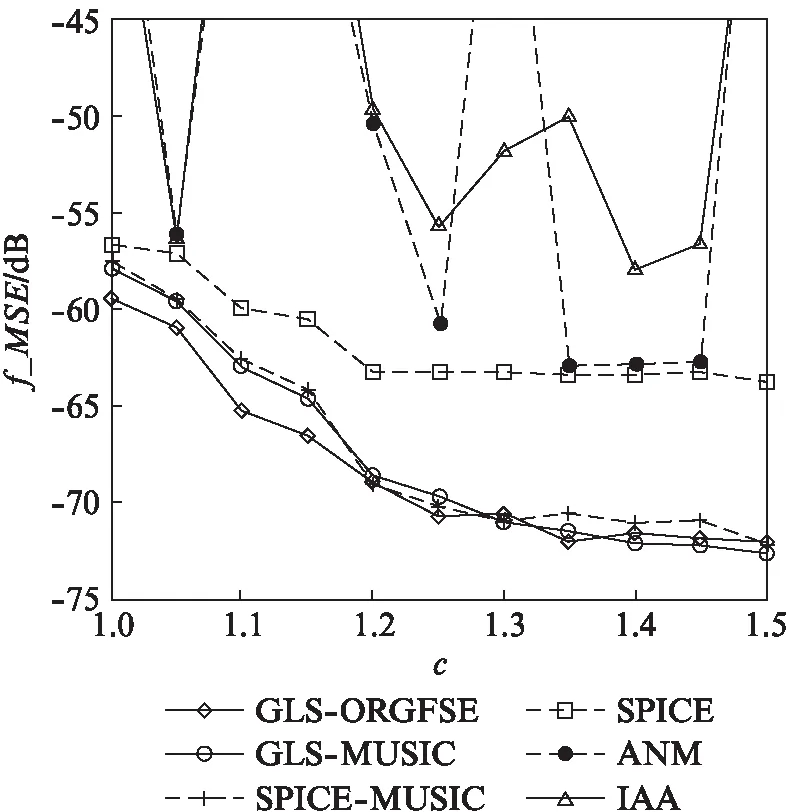
4.2 仿真实验结果





5 结 论

