具有耐药性的HIV模型研究
何 兰,宋运娜
(齐齐哈尔医学院 高数教研室,齐齐哈尔 161006)
由艾滋病病毒(Human Immunodeficiency Virus, HIV)引起免疫缺陷综合症(Acquired Immune Deficiency Syndrome,AIDS).艾滋病潜伏期平均为10~13y.据调查约有10%的新近感染者携带有至少对1~3种具有耐药性的病毒[1-3].2004年,美国对其40个城市的371名未经任何治疗的新近感染者进行了耐药性筛查.结果显示,有14%的感染者至少对1种抗病毒药物产生了耐药性[4].HIV-1耐药株在我国广泛流行.2005年,对河南省部分感染HIV-1的人群进行的耐药性调查显示,总体的耐药性突变发生率为33.87%,抗病毒治疗6个月后,耐药性突变发生率高达62.7%[5-6];2007年,在我国部分未经治疗的感染者中,耐药性HIV的流行已达15%[7].HIV耐药株产生的主要原因是病毒基因组自身在传代复制中出现错误以及抗病毒药物治疗对病毒株耐药的选择作用[8],还有长期用药的不依从性.
很多学者运用数学模型研究HIV传染病模型.Maziane等[9]研究了被感染细胞可以治愈的HIV模型,对HIV传染率函数详细分析,并引入3个参数,给出传染率改变的5种可能.
Podder等[10]研究了抗逆转录治疗,自愿测试(使用抗体标准或DNA基础的测试方法)和安全套使用情况对于HIV防控的影响,模型通过阈值界定无病平衡点全局渐进稳定.Bhunu等[11]也研究了抗逆转录治疗,针对双菌株情况进行定性分析,讨论模型的非负性、有界性和持久性.Sharma等[12]研究了关于HIV/AIDS的五仓室模型.Roy等[13]运用最优控制理论模型,研究了人们的意识(包括媒体等因素)在控制HIV/AIDS上的影响.Pitchaimani等[14]在HIV模型分析中引入了3个时滞.Wang等[15]完成了具有离散时滞的HIV-1免疫反应模型的数学分析.这里研究具有耐药性的多维HIV传染病模型.
1 模型的建立
HIV病毒传染特点是易感染者感染HIV病毒后,成为感染初期患者,在这个时期具有极强的传染性,经过10~13y的潜伏期,进入了艾滋病患者前期,并最终成为艾滋病患者.因为长时间的用药和HIV病毒基因组在传代复制中出现错误,导致一部分患者具有耐药性,具有耐药性的患者具有更强的传染性.
研究HIV传染病,我们将人群分为9类: 易感染者S,感染初期者I1,潜伏者E,艾滋病前期患者I2,艾滋病患者A,和具有耐药性的感染初期者I1*,具有耐药性的潜伏者E*,具有耐药性的艾滋病前期患者I2*,具有耐药性的艾滋病患者A*,其中模型中方程相应的参数设置为:Δ表示为加入群体的易感染者;β1,β2分别为HIV感染者和具有耐药性的HIV感染者的传染率;d为自然死亡率;a1,a2分别为普通感染和具有耐药性的感染初期患者转换为潜伏者的比率;b1,b2分别为普通感染和具有耐药性的感染潜伏者转换为艾滋病前期患者的比率;c1,c2分别为普通感染和具有耐药性的艾滋病前期患者转化为艾滋病患者的比率;d1,d2分别为普通感染和具有耐药性的艾滋病患者的死亡率;p1为普通潜伏者转化为具有耐药性的潜伏者的比率;S(t),I1(t),E(t),I2(t),A(t),I1*(t),E*(t),I2*(t),A*(t)分别表示关于时间t的函数,这里简写为S,I1,E,I2,A,I1*,E*,I2*,A*.
建立模型:
(1)
1.1 系统(1)的非负性和有界性
由系统(1)的第一个方程S′+β1(I1+E+I2)S+β2(I1*+E*+I2*)S+dS=Δ,得
同理E(t),I2(t),A(t),I1*(t),E*(t),I2*(t),A*(t)均非负.

即系统(1)的可行解都在该子区域内有界.
1.2 系统平衡点

系统(1)中,E*=I1*=I2*=A*=0,令方程左侧为零,解方程可得

与上同理,可得
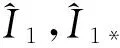
2 无耐药性平衡点的全局稳定性

证 首先我们考察系统(1)的无耐药性的5维子系统:
(2)
设S的初始时刻值为S0,β1是关于S0的函数,可得2个矩阵:

下面证明p1的全局渐近稳定性.构造Lyapunov函数:
(c1+d)(b1+d+a1)S,
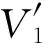
[Δ-β1(I1+I2+E)S-dS]=

[d(b1+d+a1)+a1b1](a1I1-dE)+(c1+d)(b1+d+a1)[Δ-Sβ1I2-dS-dI1-a1I1].

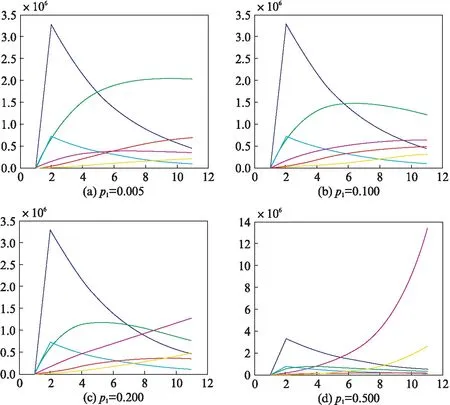
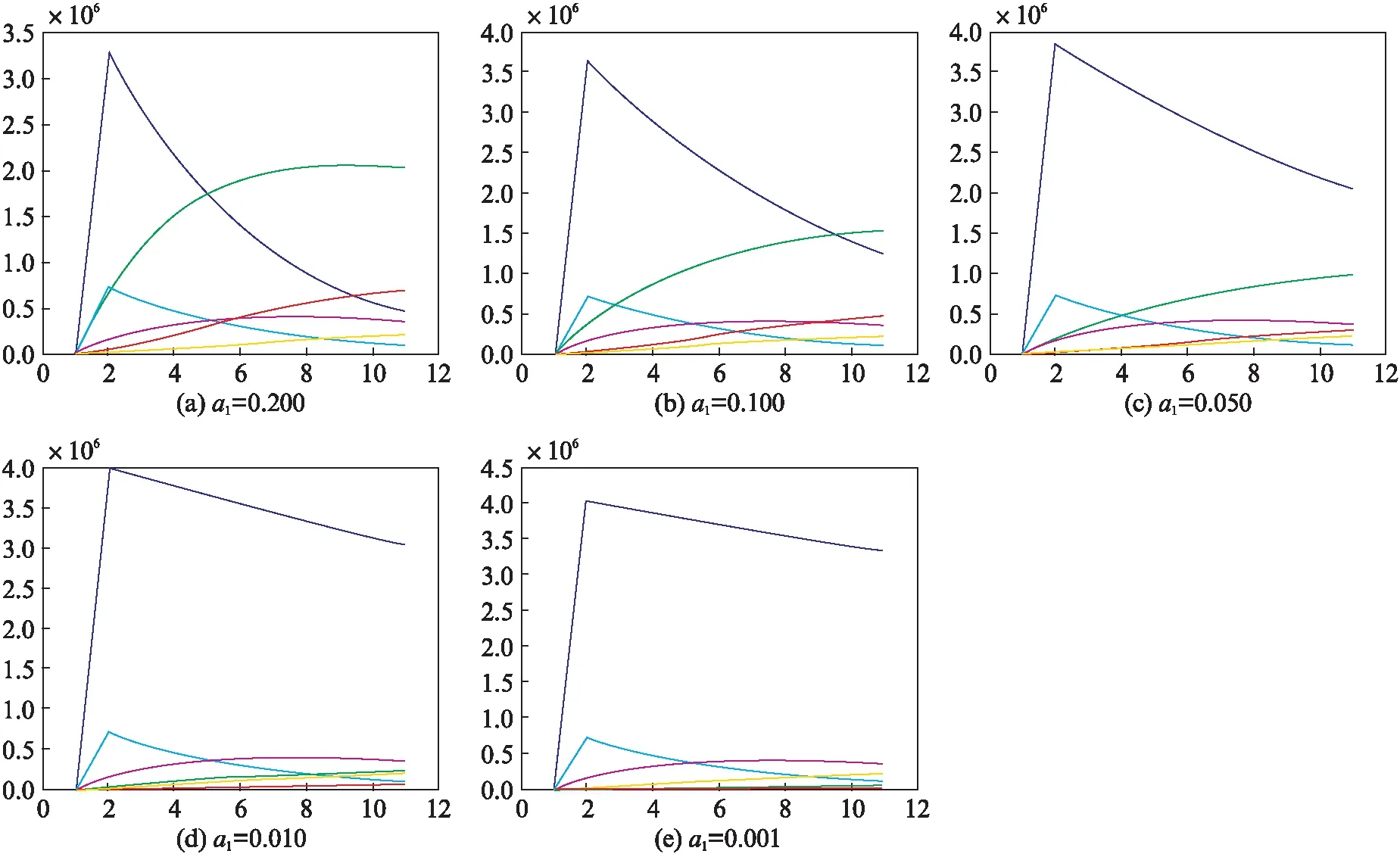
现实生活中,处在潜伏期的病人明显多于艾滋病前期的患者,设a1I1 另由系统(2)第1个方程得: Δ-β1I2S-dS=β1(I1+E)S; 再由第2个方程得: (d+a1)I1=β1(I1+E+I2)S. 上面两式相减得: Δ-β1I2S-dS-(d+a1)I1=β1(I2+E)S-β1(I1+E+I2)S=-β1I1S<0. 因为A,A*在系统(1)的另外7个方程中没有出现,所以我们考察系统(1)的7维子系统: (3) 构造Lyapunov函数: 由系统(3)的第2,第4,第5,第7个方程可得: 将上式带入函数中得: 通过数值模拟讨论参数对HIV传播的影响.结合文献[12,15],设置基本参数数值为:Δ=0.029,d=0.02,d1=0.333,d2=0.4,b1=b2=0.1,a1=a2=0.2,p1=0.02,β1=0.01,β2=0.008,c1=0.035,c2=0.095.考察国内HIV的发病率,在500万的人口群体内设置S,I1,E,I2,I1*,E*,I2*的初始值分别为: 5000000,1000,2000,1000,1000,2000,500. 图1为随着参数β2的取值变化,模型中各种群的变化图像,图中图示: 蓝线-I1,绿线-E,红线-I2,浅蓝线-I1*,紫线-E*,黄线-I2*,以下各图皆同. 图1 随着参数β2的取值变化,模型中各种群的变化图像Fig.1 The image of the population change with the change of parameter β2 values 参数β2的数值分别为: 0.005,0.008,0.010,0.020,0.030,0.050.通过图1可以看出: 固定β1=0.010时,β2的变化对传染病传播的影响.当β2=0.005时,模型主要表现为敏感的HIV疾病,随着β2的增大,具有耐药性HIV表现越来越明显,患者的总数会有所增加,当β2>0.010时,在模型中具有敏感急性患者、易感者和艾滋病前期的患者都趋近于0,人群中患病者都为具有耐药性的患者.说明具有耐药性的病毒的传染率对于疾病的控制尤为重要.并且随着β2增加,具有耐药性的HIV模型图像又基本保持不变. 图2为随着参数p1的取值变化,模型中各种群的变化图像.图2中,p1值分别为: 0.005,0.100,0.200,0.500.当p1值很小时,模型中敏感性HIV占绝对优势,但是随着p1值的增大,首先是敏感性的易感者人数不断地减少,具有耐药性的易感者人数相对增加,逐渐的具有耐药性的慢性HIV患者也增加,并且趋势增加到无穷大,最终的结果就是所有的人都将患上具有耐药性的HIV疾病,可见参数p1直接影响到具有耐药性HIV疾病的防控. 图2 随着参数p1的取值变化,模型中各种群的变化图像Fig.2 The image of the population change with the change of parameter p1 values 图3为随着参数a1的取值变化,模型中各种群的变化图像.图3中,a1取值分别为: 0.200,0.100,0.050,0.010,0.001.参数a1反映HIV疾病的药物疗效,当a1=0.200时,在a1=0.200的图像显示,疾病为耐药性和敏感性的HIV共存,但是敏感性的HIV明显占绝对优势.随着药物药效的发挥,a1取值的不断变小,具有耐药性的HIV疾病的发展没有变化,而敏感性HIV患者发生巨大的变化,感染初期者I1都是在第2个时间点上出现最大值而且最大值没有变化(由于患者自身的免疫力和药效都有一定的时滞),但是之后I1的数量随着a1变小而不断增大,E,I2的数量不断减少,甚至I2→0. 图3 随着参数a1的取值变化,模型中各种群变化图像Fig.3 The image of the population change with the change of parameter a1 values 具有耐药性的HIV疾病在现实生活中多有存在.从理论上分析,通过控制参数β2,p1的数值,减小敏感性感染初期患者转换为潜伏者的比率a1的值,可以对HIV进行防控.具体做法: 尽量阻断具有耐药性的传染源、合理规范用药,避免耐药性的产生,尽快研发出有效药物,通过药物治疗的手段减少HIV疾病的蔓延. 参考文献: [1] MENDOZA C D, RODRIGUEZ C, CORRAL A, et al. Evidence for differences in the sexual transmission efficiency of HIV strains with distinct drug resistance genotypes [J].ClinInfectDis, 2004,39(8): 1231-1238. [2] GRANT R M, KURITZKES D R, JOHNSON V A, et al. Accuracy of the TRUGENE HIV-1 genotyping kit [J].JournalofClinicalMicrobiology, 2003,41(4): 1586-1593. [3] WENSING A M, BOUCHER C A. Worldwide transmission of drug-resistant HIV [J].AIDSReviews, 2003,5(3): 140-155. [4] ROSS L, LIM M L, LIAO Q, et al. Prevalence of antiretroviral drug resistance associated and resistance mutations in antiretroviral therapy(ART) -naive HIV-infected individuals from 40 United State cities [J].HIVClinicalTrials, 2007,8(1): 1-8. [5] LI J Y, LI H P, LI L, et al. Prevalence and evolution of drug resistance HIV-1 variants in Henan, China [J].CellResearch, 2005,15(11): 843-849. [6] WANG Z, LIANG Y, XIN T Y, et al. Investigation on curative effect and drug resistance of HIV patients received HAART [J].JournalofMedicalForum, 2005,26(19): 1-3. [7] ZHANG X X, WANG C, WANG H, et al. Risk factors of HIV infection and prevalence of co-infections among men who have sex with men in Beijing, China [J].AIDS, 2007, 21 (Suppl 8): S53-S57. [8] 贾峥.HIV-1耐药性的研究进展 [J]. 中国生物制品学杂志,2011,24(8): 988-993. [9] van den DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission [J].MathematicalBiosciences, 2002,180(1-2): 29-48. [10] PODDER C N, SHAROMI O, GUMEL A B, et al. Mathematical analysis of a model for assessing the impact of antiretroviral therapy, voluntary testing and condom use in curtailing the spread of HIV [J].DifferentialEquations&DynamicalSystems, 2011,19(4): 283-302. [11] BHUNU C P, GARIRA W, MAGOMBEDZE G. Mathematical analysis of a two strain HIV/AIDS model with antiretroviral treatment [J].ActaBiotheoretica, 2009,57(3): 361-381. [12] SHARMA S, SAMANTA G P. Dynamical behaviour of an HIV/AIDS epidemic model [J].DifferentialEquations&DynamicalSystems, 2014,22(4): 369-395. [13] ROY P K, SAHA S, BASIR F A. Effect of awareness programs in controlling the disease HIV/AIDS: An optimal control theoretic approach [J].AdvancesinDifferenceEquations, 2015,2015(1): 1-18. [14] PITCHAIMANI M, MONICA C. Global stability analysis of HIV-1 infection model with three time delays [J].JournalofAppliedMathematics&Computing, 2015,48(1-2): 293-319. [15] WANG Z W, WANG W D. Mathematical analysis of immune response of HIV-1 including delay [J].ChineseQuarterlyJournalofMathematics, 2010,25(1): 45-51.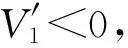
3 具有耐药性平衡点的全局稳定性
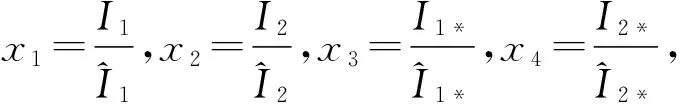
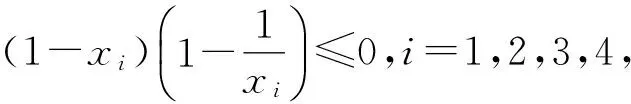
4 数值模拟

5 结 语

