考虑组内网络效应的平台定价机制研究

石 雪，徐 庆

(青岛大学 商学院，青岛 266071)

近几年来，随着网络技术的不断发展，各种购物平台、交友平台层出不穷，像淘宝、京东、链家网以及一些婚介平台正在如火如荼的运作中.我们也都看的出来，现代许多产业是围绕平台来建立的，买卖双方通过这个平台来进行交易，并且双方之间互相影响.买方选择该平台是因为有许多卖方在平台上出售自己的商品，买方可以有多个选择；卖方选择该平台是因为平台上聚集了大量的买方，有一定的市场.

目前，关于双边市场概念的界定有多种说法，但是大多以Armstrong[1]的说法为准，即从网络外部性这方面来看，市场上双方参与者需要通过一个平台来进行交易，并且一方参与者的效益与另一方参与者的人数有关.现实生活中关于双边市场的例子也有很多，比如说购物商场，它能促进消费者和零售商之间的交易；信用卡平台允许买方和批发商之间用信用卡进行支付；报纸使得信息在广大读者和广告商之间传播；二手车平台促进了买车者和卖车者之间的交易.所以说，平台作为连接买方与卖方市场的中介，承担着信息交换的使命，它也正是通过信息的提供来获得利润，因此，平台如何对买方和卖方收取服务费以获取更高的利润就显得尤为重要.

国外对双边市场的研究较早的是Rochet和Tirole[2]，他们假设平台对双方参与者不收取固定费用而只收取单笔交易费用，最终得到平台对参与双方的定价是与双方的需求弹性负相关的，也就是说市场双方的需求越大，平台对其收取的费用就会越低，并且平台对双方收取费用的比值等于双方需求弹性之比.Krueger[3]通过运用线性需求函数进行实证分析，证实Rochet和Tirole关于平台企业双边用户的需求价格弹性对定价策略的影响.一般这种只收取单笔交易费用的模式适用于电子商务市场，与这种定价模式不同，Armstrong考虑的是对市场双方收取固定费用，他认为平台的定价是与市场参与者提供的网络外部性相关的，提供网络外部性较多的一方相应的定价就会较低，而提供网络外部性较低的一方相应的定价会较高.这种模式适用于媒体、网络等双边市场.随着双边市场应用越来越广，对它的研究也越来越多，但是随后的研究一般以这两种模式为基础.比如Weyl[4]对垄断平台的双边定价进行研究，并认为垄断平台的最优定价等于为人数增加一方所付出的单位服务成本减去该方参与者为另一方参与者所带来的单位效益.而Gabszewicz和Wauthy[5]则是研究了异质型的双边市场，即他们认为市场参与者一方之中的每个参与者能够获得的效用是不一样的，并通过求解得出了平台的最优定价.Reisinger[6]也研究了异质型的双边市场，并且对双方参与者进行了二部制定价，得到了最优定价的唯一均衡.

国内对双边市场的研究也有很多.例如，程贵孙[7]将自网络外部性引入了双边市场定价模型中，研究自网络外部性和交叉网络外部性共同作用下的双边市场定价问题，通过建立定价博弈模型，得到了多重作用下的双边市场价格均衡.白莹[8]则是结合网络团购平台的特点，通过引入交叉网络外部性、差异化程度、卖方信誉及平台搜索匹配度，建立了专门针对团购平台的双边市场定价模型，并通过分析发现平台需要对网络外部性较强、差异化程度较小的一方收取较低的交易费，网络团购平台需通过不断提高差异化程度和卖方信誉等方式，来吸引更多用户并达成更多交易量，从而使团购平台真正获得盈利.张文强[9]也研究了双边市场中团购网站的定价策略，他指出团购网站对接入用户进行一定的价格补贴在一定程度上增加了买卖双方的交叉网络外部性.王巧玲[10]通过论述网络团购的发展现状，指出网络团购的价格结构有着明显的双边市场特征，平台对买卖双方的收费会直接影响双方对平台的选择，另外，买卖双方之间的交叉网络外部性也影响着他们各自的效用.阳成虎等[11]发现： 团购平台有时会向接入平台的商家收取较高的佣金而向消费者免收交易费或者对其进行补贴，这在一定程度上损害了商家的利益，所以，平台应该提升自身的服务质量并实行差异化战略，吸引更多消费者以提升商家的网络外部性.正如淘宝、京东等购物平台不向消费者收取注册费用而只是向入驻平台的商家收取费用，若是淘宝向消费者收取费用的话，消费者可能选择去逛京东，那么淘宝上的交易量就会有所损失.

以上国内外的研究着重分析了消费者与商家之间的交叉网络外部性对平台定价的影响以及平台收取费用的方式对自身利润的影响.在现实生活中，网络覆盖率的提升吸引了各种各样平台的建立，相同或者相似的平台之间的竞争也日益激烈.一些商家为了吸引更多的消费者，可能会在多个平台上销售自己的产品，而消费者为了能有更多的选择，也可能会在多个平台上浏览商品.所以说，在双边市场中，消费者与商家之间的交叉网络外部性逐渐被弱化，因为在整个市场中，接受并实际去网络平台上购物的消费者已经有很多，市场上也有大量的商家通过网络平台来销售自己的产品.正如在淘宝这个购物平台上，一个消费者要买一双鞋子，她不会过多关注淘宝上有多少出售鞋子的商家，因为平台上商家已经成千上万，想要浏览完全部商家不太现实；同理，一个商家也并不会过多考虑消费者浏览量增加几个或者几十个，因为每天在平台上浏览商品的消费者数量差别不会太大.而当一个购物平台刚出现的时候，无论是消费者还是商家，都有可能会参与这个平台，他们更为关注的是自身所获得的效用，比如平台的服务质量、产品价格等因素，因为一个平台如果做得好的话，总会有大量的消费者和商家在平台上进行交易.但是我们都知道，有限的资源只能服务有限的人数.在消费者一方，由于消费者人数的增多，不论是商家的服务还是消费者浏览网页的速度都会有所减慢，除此之外，由于消费者对个性化的追求，当消费者一方人数不断增多的时候，消费者的边际效用会降低.在商家一方，商家数目越多，他们之间的竞争会更加激烈，边际效用也会存在递减的情形.就像“饿了么”和“美团”这两个外卖平台，会有很多的商家出售商品，也有很多消费者在这两个平台上订外卖.在这个时候，消费者不会考虑这个平台上有多少商家，而考虑的却是在该平台上下单会多久送到，或者是外卖的质量，即好不好吃.而如果一个商家的服务水平是每天100份，那么，当有120个消费者订外卖时，质量以及服务水平势必会下降，则消费者的边际效用就会降低.消费者边际效用的降低势必会影响平台的效益，正如“3·15”报道的“饿了么”事件.而在以往的研究中多建立线性效用函数，未考虑效用递减的情况.所以，基于以上说明，本文考虑了两个相互竞争的平台，在两个平台存在可替代性的情形下，引入了非线性效用函数，更多地考虑了消费者和商家的组内网络效应(即群体内的相互影响)，以及消费者和商家效用递减情况，建立了平台定价模型，研究和分析了平台的定价策略.研究结果对竞争市场中的平台企业和新进入市场的平台企业具有一定的借鉴作用.

1 模型假设及符号

本文研究基于市场上存在两个相互竞争的平台i和平台j，消费者可以在两个平台上浏览商品，进行交易.同理，商家也可以在两个平台上进行商品的展示与销售.消费者与商家都会基于自身效用最大化来选择要加入的平台.一开始，消费者会认为产品的质量有保证，或者是该平台的服务较好.而随着消费者人数的不断增多，消费者的个性化被减弱，并且，由于平台总的服务能力一定，消费者人数的增多势必会降低单个消费者获得的效用.同理，在商家一方也是如此，一开始，商家会到该平台上进行商品的展示，而随着商家个数的不断增多，商家之间的竞争也不断加剧.因此，根据效用递减的原理，建立如下消费者的效用函数：

(1)

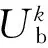
同理，商家的效用函数可以表示为：

(2)

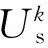
下面，给出本文的假设条件.

(1) 市场上存在两个平台，并且两个平台之间存在竞争.两个平台之间的可替代系数0<θ<1.当θ=0时，表示两个平台上销售的产品完全不同，两个平台无法相互替代；当θ=1时，表示两个平台销售完全相同的产品，其中一个平台可以被另一个完全替代.本文不考虑以上两种极端情况，考虑的是两个平台不完全相同但是又不可以完全相互替代的情况，所以令0<θ<1.

(2) 消费者与商家的初始效用都为0.

(3) 无论是消费者还是商家，他们获得的单位效用总是大于平台为他们所付出的单位成本，即αb>Cb，αs>Cs(其中Cb代表平台为消费者服务所付出的单位成本，Cs代表平台为商家服务所付出的单位成本)，且成本不为0.

(4)网络平台上有足够多的消费者会在平台上购买商品，也有大量的商家会在网络平台上销售产品，因此仅考虑组内网络外部性，也即群体内的相互影响(例如消费者去淘宝购买商品，由于商家已经足够多，此时消费者不会过多地考虑平台上有多少家商家在出售该种商品，而更多考虑的是商品的质量、平台的售后服务、个性等因素)，同理商家也是如此.

2 模型建立

在现实生活中，许多网络平台如淘宝、京东商城等并不会对广大消费者收取平台服务费，而只是对入驻平台的商家收取一定的费用，因为如果某一个购物平台向消费者收取费用的话，消费者将会去不收费的平台购物，从而向消费者收取费用的平台将会损失巨大的交易量.因此，在这种情况下，购物平台只对商家收取费用，那么平台的收益可以表示为：

(3)

(4)

令一阶导数等于零，求解得到在消费者追求效用最大化过程中，平台i和j上最优的消费者人数：

(5)

(6)

很明显，在现实中，消费者数量总是大于0，所以根据式(5)和(6)可知：

θ

同理，根据式(2)的商家效用函数，求解得到的平台i和j上商家的个数：

(7)

(8)

由于商家个数也是非零的，证明在命题2中体现.

将式(7)及(8)分别代入式(3)和(4)式中，可以表示出平台的收益为：

(9)

(10)

命题1在平台只对商家收取费用的前提下，存在使得平台利润最大化的最优均衡价格.

令以上2式都等于零，即可求得平台向商家收取的最优价格为：

(11)

(12)

(13)

(14)

先看式(13)，将其经过线性变换后可以得到：

(15)

(16)

命题3平台对商家的最优收费P随着θ(两个平台之间的替代性)的增加而减少，即两个平台之间的差异越小，平台对商家收取的费用也会越低.

所以对θ求一阶导数得：

由于分母总是大于零的，所以只要研究分子即可.

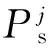
在现实生活中，命题3也是有迹可循的.比如说当市场上只存在一个销售化妆品的平台，商家要想在该平台上销售自己的产品，必然需要付给平台一部分服务费用，这个时候由于商家较多而平台只有一个，平台可以收取较高的服务费用.而当市场上又出现另一个与之相似的平台时，商家有了可选性，为吸引商家入驻或是留住已经入驻的商家，此时平台对商家收取的服务费用就会有所降低.

3 算 例

为了更为形象直观地说明命题的准确性，以下是相关的数值分析.

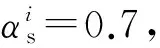
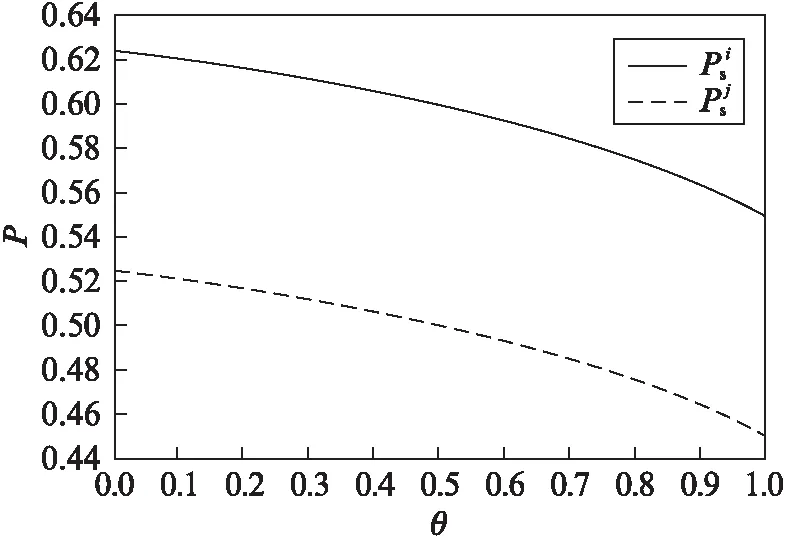
图1 平台对商家收取费用与平台替代性关系图Fig.1 Relationship between and θ

图2 平台上商家个数与平台替代性关系图Fig.2 Relationship between and θ

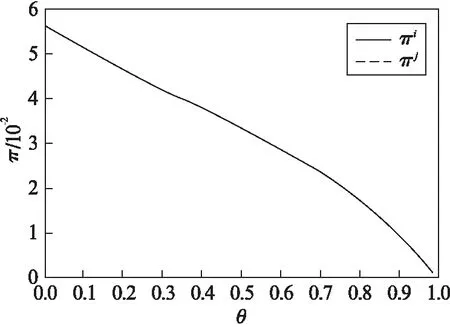
图3 平台利润与平台替代性关系图Fig.3 Relationship between πi, πj and θ

(3) 对于两个平台的利润，我们采用与图2相同的参数设置，将两个平台的替代性系数θ作为自变量，将平台利润π作为因变量，得到了如图3所示的结果.

表1 平台i有优势时可替代性系数变化对各平台商家个数、价格及平台收益的影响

从表1可以看出，当平台之间的可替代性(θ)较小的时候，平台上的商家个数差别并不是很大.而随着平台间可替代性的增大，即两个平台之间的差异不断减小，则两个平台上的商家个数的差别也随之增加.当θ增大到0.90时，两个平台上的商家个数相差就非常大了.由于平台i为优势一方，所以平台i上的商家个数随θ的增加呈现不断增长的趋势；而平台j为劣势的一方，平台j上的商家个数随着θ的增加大幅度减少以至于被挤压出市场(θ=0.90时，平台j上的商家个数已接近0).对于两个平台对商家收费的情况，依然会呈现如图1所示的变化趋势，随着θ的增大而减小，但都不会低于平台所付出的成本.对于平台的收益情况，我们发现当θ并不太大的时候，平台的收益都是随着θ的增大而减小的，这也说明随着两个平台差异的减小，平台之间的竞争加剧使得两个平台的收益都减小，这与图3中平台的利润有着相同的走势.但当θ=0.90时，平台j的收益已经接近于0，当θ继续增大时，平台j上的商家个数为0，收益自然也为0.此时平台j由于缺乏优势会退出市场，此时市场上只存在平台i，所以平台i的收益呈现递增的趋势.

表2 平台j有优势时可替代性系数变化对各平台商家个数、价格及平台收益的影响

总之，一个平台要想在市场中存活下来，一方面可以凸显出自己的独特性，在平台的页面设置、销售的商品或者是服务水平上与其他的平台有较大的差异，使得可替代性系数θ小一些；另一方面，就是提升自己的水平，使得提供给消费者和商家的效用提高的同时降低自身的服务成本，从而成为有优势的一方.

4 结 语

本文针对市场中的平台定价问题进行了研究.通过建立消费者和商家的效用函数和平台的收益模型并且在求解分析后发现： 平台对商家的收费是随着平台间可替代性系数的增大而降低的；当两个平台竞争力相同时，会存在均衡状态；当两个平台竞争力不同时，若平台可替代性较小，两个平台还可以共存.但是当可替代性系数达到某一个程度，优势一方会独占市场而缺乏优势一方会退出市场.所以，一个平台若是想要存活下来或者是一个新的平台要进入市场，一方面可以提高自身的服务水平以及产品质量，以此来提高提供给消费者和商家的效用；另一方面也可以通过彰显自身的独特性，从而降低平台间的可替代性系数.

参考文献：

[1] ARMSTRONG M. Competition in two-sided markets [J].RANDJEcon, 2006，37： 668-691.

[2] ROCHET J C, TIROLE J.Platform competition in two-sided markets [J].JEurEconAssoc, 2003(1)： 990-1029.

[3] KRUEGER M. 11le elasticity pricing rule for two-sided markets： A note [J].ReviewofNetworkEconomics, 2009,8(3)： 271-278．

[4] WEYLE G. A price theory of multi-sided platforms [J].AmEconRev, 2010,100： 1642-1672.

[5] GABSZEWICZ J J, WAUTHY X Y. Vertical product differentiation and two-sided markets [J].EconomicsLetters, 2014,123： 58-61.

[6] REISINGER M. Two-part tariff competition between two-sided platforms [J].EuropeanEconomicReview, 2014,68： 168-180.

[7] 程贵孙.组内网络外部性对双边市场定价的影响分析 [J].管理科学，2010，23(1)： 107-113.

[8] 白莹，李明杰，袁冲，等.基于双边市场的网络团购平台定价模型研究 [J].北京邮电大学学报,2012,14(2)： 52-57.

[9] 张文强.基于双边市场理论的团购网站定价模型研究 [J].中国商贸,2012(30)： 94-95.

[10] 王巧铃.电子商务背景下网络团购促销定价策略研究 [J].价格月刊,2015(4)： 73-77.

[11] 阳成虎,林志云,王力.基于双边市场的网络团购平台运作策略 [J].福州大学学报(哲学社会科学版),2015,29(4)： 16-20.