存在有限导流断层的油藏压力动态分析
曾 杨 康晓东 谢晓庆 未志杰
1.海洋石油高效开发国家重点实验室, 北京 100028;2.中海油研究总院有限责任公司, 北京 100028
0 前言
有关封闭断层的试井研究已经趋于成熟,但国内外对非封闭断层的研究较少,特别是对有限导流断层的研究尚处于起步阶段[1-6]。目前,Horner D R半对数曲线法是判别封闭断层的常用方法[7]。1975年,Prasad R K、Tiab D和Earlougher R C等人[8-10]研究了多条交叉以及平行的封闭断层模型井底压力响应特征。Bixel H C等人[11]最先提出存在非封闭断层边界的试井解释模型,但他仅考虑流体性质和岩石在平面上突变的情形,且求解方法复杂,Kuchuk F J等人[12]后来改进和完善了该模型的求解方法。1984年,Stewart G和Streltsova T D等人[13-14]基于Bixel H C的研究模型,运用数值模拟方法研究了干扰试井曲线受部分连通断层的影响程度。1987年,Yaxely L M[15]求解了存在部分连通断层的无限大均质油藏模型的解析解。Ambastha A K等人[16]在此基础上进一步研究了存在部分连通断层边界的复合油藏中井底压力响应特征。但是,Bixel H C、Yaxely L M、Ambastha A K等人所建立的模型没有考虑断层内部存在流体流动,仅考虑了断层允许两边地层流体流动的情形。当附近储层的渗透率小于断层的渗透率时,流体会在断层内部流动,此时断层表现出有限导流裂缝的特征。Maghsood A和Heber C L[17]的研究忽略了断层内部压力瞬态变化,仅考虑了断层的导流能力,模型的精度不能保证。因此,本文建立了存在有限导流断层的复合油藏试井解释新模型,并且考虑断层内部流体瞬态变化,通过数学运算得到模型半解析解。利用Stehfest H等人[18-20]数值反演求得了实空间的压力解,最后绘制了模型的典型曲线并分析了曲线的影响因素,为类似油藏的试井解释提供了理论指导和技术支持。
1 渗流物理模型
如图1~3所示,本次研究将存在有限导流断层的渗流问题简化为无限大地层中定产量生产的一口激动井的压降分布问题,且地层中含有一个没有交叉的有限导流断层。断层两侧的储层区域岩石特性及渗透率不同,有限导流断层的渗透率大于两侧储层的渗透率,储层流体允许通过并沿断层流动,但断层没有存储能力,断层面的表皮系数为Sf,传导系数为FCD。其假设条件为:
1)有限导流断层两侧为均质油藏,岩石特性及渗透率不同。
2)两边油藏流体为单向微可压缩液体,压缩系数及黏度保持不变,流动服从达西定律。
3)断层两侧的储层厚度相同。
4)激动井为无限大线源。
5)忽略重力和毛管力的影响。
6)整个地层具有相同的初始压力。

图1 存在有限导流断层的油藏示意图
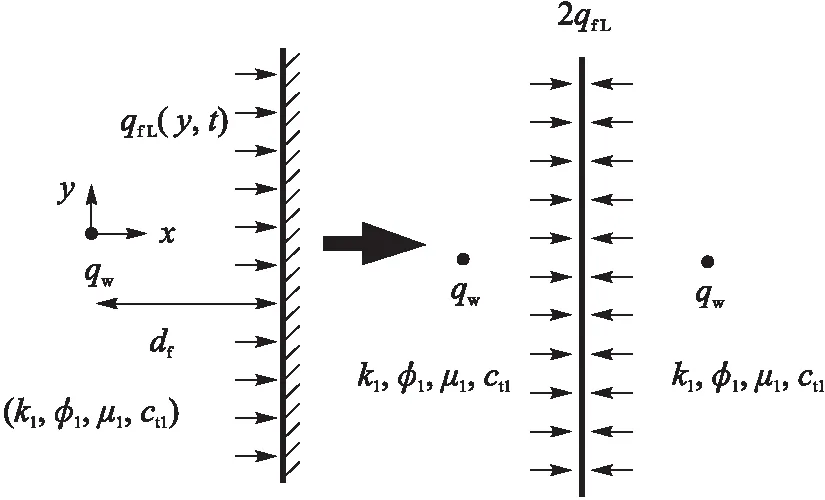
图2 断层左侧油藏流体流动镜像示意图

图3 断层右侧油藏流体流动镜像示意图
2 数学模型的建立及求解
2.1 断层内部流体流动压力研究
根据图1所建立的坐标系和上述假设条件,以基本的渗流力学理论为依据,可推出断层内部流体流动的试井解释模型。
2.1.1 渗流微分方程
(1)
2.1.2 边界条件
(2)
pfD(yD=+∞,-∞)=0
(3)

(4)
上述无因次变量:
无因次压力
(5)
无因次时间
(6)
无因次流量
(7)
无因次距离
(8)
断层的传导系数
(9)
式中:pf为断层内部的压力,MPa;k1、kf、ka分别为左侧油藏、断层、变动区渗透率,10-3μm2;h、wf分别为地层厚度、断层厚度,m;df为断层到激动井的距离,m;μ1为左侧油藏的黏度,mPa·s;φ1为左侧油藏的孔隙度,小数;Ct1为左侧油藏综合压缩系数,MPa-1。
对方程(1)进行从0→yD,yD→∞的双重积分,并代入边界条件(2)~(4)得到:
(10)
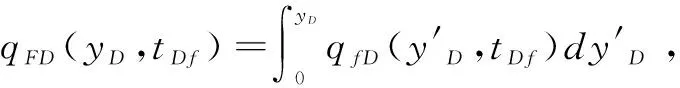
(11)
对式(11)进行Laplace变换,得到:
(12)
2.2 左侧油藏的流动压力研究
根据图2所示,断层左侧的半无限大油藏可以看为一个以定产量qw生产的激动井和一个流量qfL随位置和时间变化的断层系统。由于流体在这个区域的流动为线性流,根据镜像原理,系统可以转变为以断面为镜像的无限大油藏中有两个强度qw的持续点源和强度2qfL随位置和时间变化的面源系统。运用点源函数法和叠加原理,可以得到断层左侧油藏的压降公式:

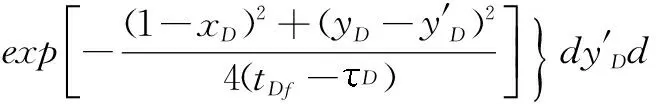
(13)
式(13)中无因次变量:
无因次压力
(14)
无因次时间
(15)
无因次流量
(16)
无因次距离
(17)
式中:pL为左侧油藏的压力,MPa;qfL为左侧油藏流入断层的流量,m3/d;x、y为横、纵坐标。
对式(13)进Laplace变换,得:

(18)
2.3 右侧油藏的流动压力研究
断层右侧油藏流体流动镜像示意图见图3,同断层左侧油藏流动相同,为求得右侧油藏的压力,根据镜像原理,可将右侧流量为qfR的断层系统看作强度2qfR随位置和时间变化的面源系统。同求断层左侧油藏的压降公式一样,我们可以得到断层右侧油藏的压降公式为:
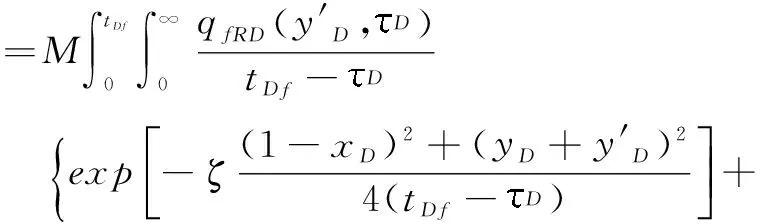
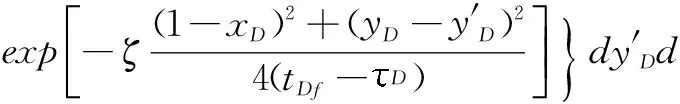
(19)
式(19)中无因次变量:
无因次压力
(20)
无因次时间
(21)
无因次流量
(22)
流度比
M=(k1/μ1)/(k2/μ2)
(23)
导压系数比
ζ=(k1/φ1μ1Ct1)/(k2/φ2μ2Ct2)
(24)
式中:pR为右侧油藏的压力,MPa;qfR为右侧油藏流入断层的流量,m3/d;k2为断层右侧油藏的渗透率,10-3μm2;φ2为断层右侧油藏的孔隙度,小数;μ2为断层右侧油藏流体的黏度,mPa·s;Ct2为右侧油藏流体的综合压缩系数,MPa-1。
对式(19)进Laplace变换,得:

(25)
2.4 断层及油藏流体流动的离散化研究
断层被划分为Nf段不等距的部分,其中最短的部分靠近界面y=0,见图4。

图4 断层离散化示意图
由式(12)知,在y方向上第j段的压力为:
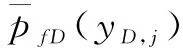
(26)
假设对于每小段,qFD(yD)是线性变换的,化简整理得:
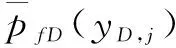
(27)
对两边油藏的压力解进行离散化,则由式(18)~(25)得:

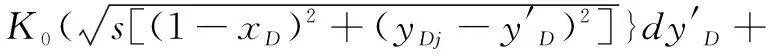
(28)
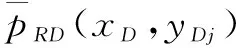

(29)
当x=rw,y=0时,由式(28)可以求得井底压力为:
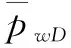
(30)

2.5 断层及油藏流体流动的耦合研究
将油藏和断层中的流动在断层面上进行耦合,由于压力和流量之间的关系,通过求得油藏中的流量即可求得油藏中的压力分布。在耦合的过程中,断层附近的过渡带需要考虑,见图1。从断层到过渡带的压降可以通过Darcy定律求得,并且考虑油藏中的所有压降得到:
(31)
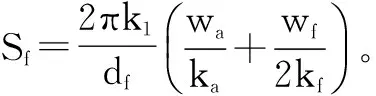
对式(31)进行Laplace变换得:
(32)
3 典型曲线的绘制及特征分析
根据求得的Laplace空间井底压力,采用Duhamel原理考虑井储和表皮的影响,通过Stehfest数值反演方法对其进行Laplace逆变换,利用计算机编程技术,绘制存在有限导流断层的油藏试井典型曲线,下面对典型曲线特征及主要影响因素进行分析。
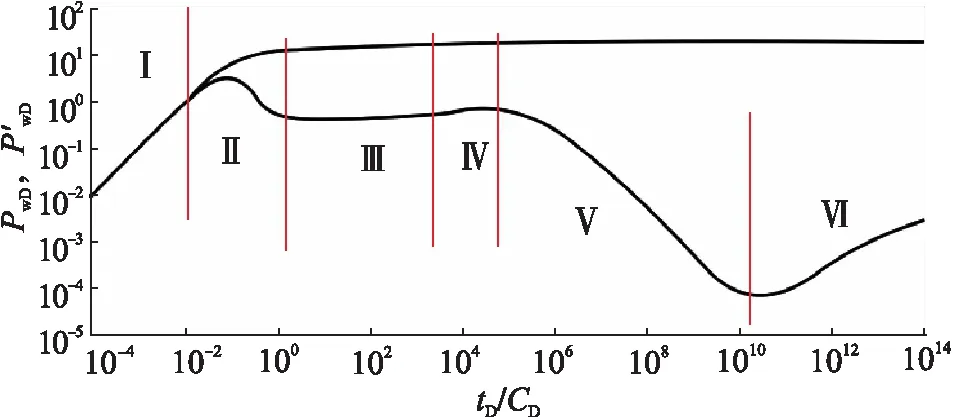
图5 存在有限导流断层的油藏井底压力曲线图版
存在有限导流断的油藏井底压力曲线图版见图5。从图5可知,存在有限导流断层的复合油藏试井模型特征曲线共有6个阶段:第Ⅰ段与普通断层特性相同,反映井筒储集阶段的压力特征;第Ⅱ段是井筒储集阶段向I区径向流的过渡段;第Ⅲ段与常规油藏径向流阶段相同,出现0.5水平线;第Ⅳ段是流体由I区径向流向有限导流断层界面的过渡段,断面表皮系数的大小影响曲线的上翘程度;第Ⅴ段为流体从断层流向Ⅱ区地层;第Ⅵ段是线性流阶段,描述了整个系统的流动,压力导数表现为1/2斜率的直线。
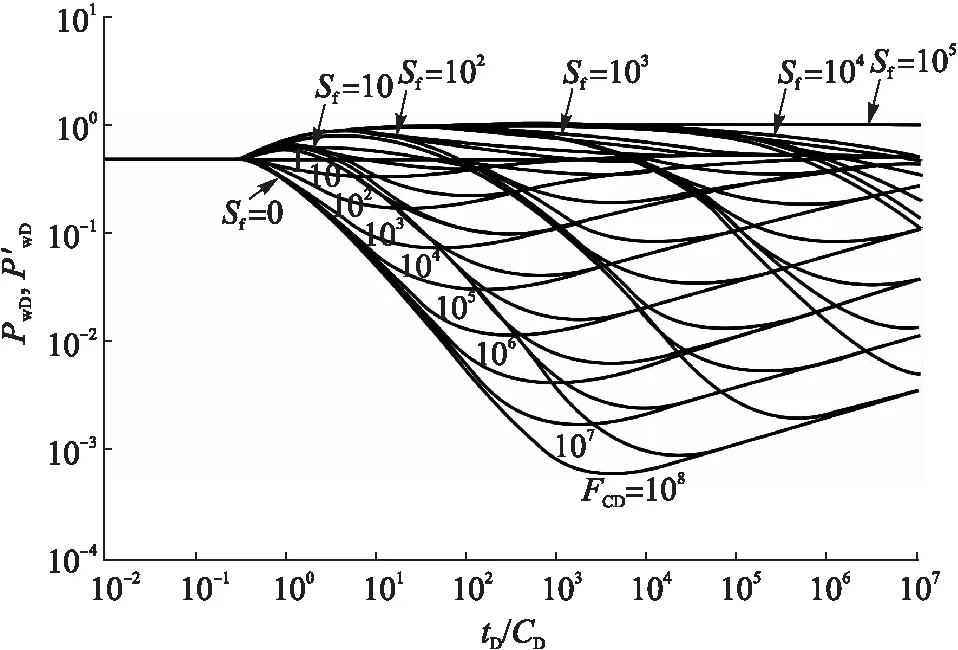
图6 断层面的特征参数(Sf和FCD)影响的典型曲线图版
断层面的特征参数(Sf和FCD)影响的典型曲线图版见图6。从图6可知,随着断层面表皮系数Sf值的增大,压力导数曲线逐渐从0.5水平线开始上翘,并且Sf值越大,曲线上翘越多。当Sf值足够大时,压力导数曲线上升到值为1的水平线,表现为封闭断层的特征。当FCD>0时,由于断层内部的渗透率大于两边储层的渗透率,流体流动能力增加,压降减小,压力导数曲线出现下凹,且FCD值越大,曲线下凹越多。当FCD值足够大时,压力导数曲线表现为斜率为-1的特征,此时类似于定压边界的反应。
4 实例应用
已知某油田生产井以844 m3/d的产量生产了1 872 h,油藏及水体相关参数如下:井径rw=0.208 m,厚度h=32.5 m,渗透率k=300×10-3μm2,孔隙度φ=0.25,原油黏度μ=0.347 mPa·s,综合压缩系数Ct=0.9×10-3MPa-1,体积系数为1.812。采用前面所述方法绘制典型曲线图版,计算有限导流断层不同界面表皮、无因次导流能力下的压力降落值。
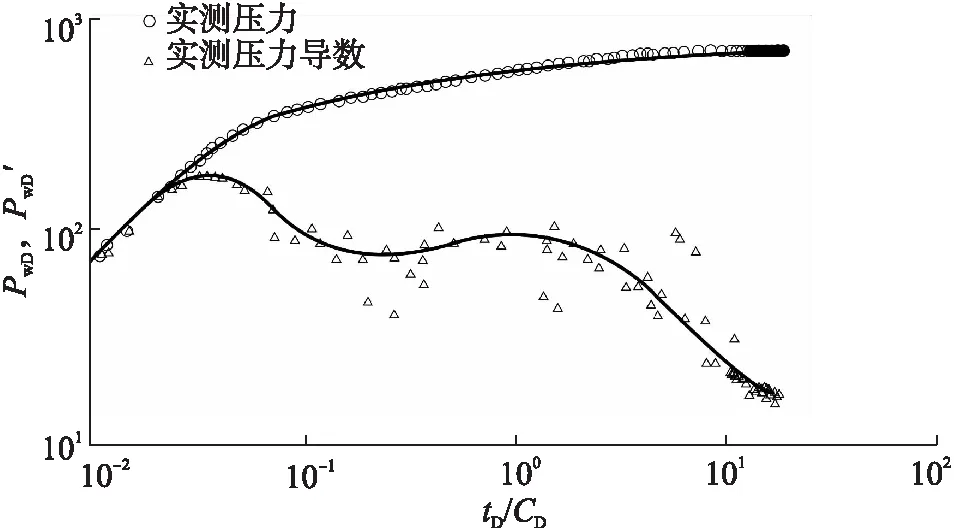
图7 某油田生产井实测数据与典型曲线拟合图
首先利用本文编制的实测离散压力点求导程序对压力差进行求导,观察其压力和压力导数变换规律,结合该区的地质研究,选用本文模型进行拟合,拟合后的双对数曲线见图7,拟合结果为:井筒储集系数3.41 m3/MPa,表皮系数2.35,渗透率6.5×10-3μm2,井到断层的距离为70.1 m,断层传导系数为10 000,断层面的表皮系数为100。
5 结论
1)建立了既考虑流体沿断层面的流动,又考虑断层内部流体流动的有限导流断层试井解释新模型,对具有类似边界条件的油藏研究和应用具有一定借鉴意义。
2)断层的传导系数FCD的大小反映流体流动性能的好坏,当FCD达到极限时,断层边界的影响与定压边界相同,压力导数表现为斜率为-1的特征;流体流动阻力的大小受断面表皮系数Sf的影响,Sf越大,阻力越大,压力及压力导数曲线位置越靠上,当Sf达到极限时,近似于封闭断层反应。
3)实例应用证明本文模型的可靠性与实用性,为具有类似边界的油藏试井解释提供了研究基础和理论依据。
参考文献:
[1] 张望明,曾 萍.存在局部连通断层的复合油藏不稳定试井分析及典型曲线拟合方法[J].石油勘探与开发,1992,19(2):69-76.
Zhang Wangming, Zeng Ping. Transient Pressure Testing Analysis and Type-Curve Matching in a Composite Reservoir with a Partially Communicating Fault [J]. Petroleum Exploration and Development, 1992, 19 (2): 69-76.
[2] 李传亮.非封闭断层的试井解释方法[J].新疆石油地质,1997,18(4):370-376.
Li Chuanliang. Interpretation of Non-Closed Fault by Applying Well Testing Method [J]. Xinjiang Petroleum Geology, 1997, 18 (4): 370-376.
[3] 王 奎,杨 静,侯光宗,等.断层封闭性研究现状及其发展趋势[J].断块油气田,2008,15(3):43-45.
Wang Kui, Yang Jing, Hou Guangzong, et al. Present Status and Development Tendency of Research on Fault Closure Property [J]. Fault-Block Oil & Gas Field, 2008, 15 (3): 43-45.
[4] 张 旭,刘启国,张小龙,等.断层板状油藏斜井试井模型研究[J].天然气与石油,2012,30(5):60-67.
Zhang Xu, Liu Qiguo, Zhang Xiaolong, et al. Research on Inclined Well Test Model for Slabby Fault Reservoir [J]. Natural Gas and Oil, 2012, 30 (5): 60-67.
[5] 张小龙,杨志兴,时 琼,等.应力敏感低渗透气藏不稳定渗流特征研究[J].天然气与石油,2016,34(1):79-82.
Zhang Xiaolong, Yang Zhixing, Shi Qiong, et al. Study on Unstable Seepage Flow Characterization in Stress Sensitivity Low Permeability Gas Reservoir [J]. Natural Gas and Oil, 2016, 34 (1): 79-82.
[6] 暴喜涛,李顺初,肖绪霞,等.均质油藏非线性渗流模型解的相似构造法[J].天然气与石油,2012,30(5):47-51.
Bao Xitao, Li Shunchu, Xiao Xuxia, et al. Similar Constructive Method of Solutions of Nonlinear Seepage Model for Homogeneous Reservoir [J]. Natural Gas and Oil, 2012, 30 (5): 47-51.
[7] Horner D R. Pressure Build-Up in Wells [C]//Paper 4135 Presented at the 3rd World Petroleum Congress,28 May-6 June 1951, Hague, Netherlands. New York: SPE, 1951.
[8] Prasad R K. Pressure Transient Analysis in the Presence of Two Intersecting Boundaries [J]. Journal of Petroleum Technology, 1975, 27 (1): 89-96.
[9] Tiab D, Kumar A. Detection and Location of Two Parallel Sealing Faults Around a Well [J]. Journal of Petroleum Technology, 1980, 32 (10): 1701-1708.
[10] Earlougher R C, Ramey H J, Miller F G, et al. Pressure Distributions in a Rectangular Reservoirs [J]. Journal of Petroleum Technology, 1968, 20 (2): 199-208.
[11] Bixel H C, Larkin B K, Van Poolen H K. Effect of Linear Discontinuity on Pressure Buildup and Drawdown Behavior [J]. Journal of Petroleum Technology, 1963, 15 (8): 885-895.
[12] Kuchuk F J, Habashy T M. Pressure Behavior of Laterally Composite Reservoir [J]. SPE Formation Evaluation, 1997, 12 (1): 47-56.
[13] Stewart G, Gupta A, Westaway P. The Interpretation of Interference Tests in a Reservoir with a Sealing and a Partially Communicating Faults [C]//Paper 12967 Presented at the European Petroleum Conference,25-26 October,1984, London, England. New York: SPE, 1984.
[14] Streltsova T D, McKinley R M. Effect of Flow Time Duration on Buildup Pattern for Reservoirs with Heterogeneous Properties [J]. Society of Petroleum Engineers Journal, 1984, 24 (3): 294-306.
[15] Yaxely L M. Effect of Partially Communicating Fault on Transient Pressure Behavior [J]. SPE Formation Evaluation, 1987, 2 (4): 590-598.
[16] Ambastha A K, McLeroy P G, Grader A S. Effect of a Partially Communicating Fault in a Composite Reservoir on Transient Pressure Testing [J]. SPE Formation Evaluation, 1989, 4 (2): 210-218.
[17] Maghsood A, Heber C L. Pressure-Transient Behavior in a Reservoir with a Finite-Conductivity Fault [J]. SPE Formation Evaluation, 1995, 10 (1): 26—32.
[18] Stehfest H. Numerical Inversion of Laplace Transforms [J]. Communications of Association for Computing Machinery, 1970, 13 (10): 624.
[19] Everdingen A F, Hurst W. The Application of the Laplace Transformation to Flow Problems in Reservoirs [J]. Journal of Petroleum Technology, 1949, 1 (12): 305-324.
[20] Hurst W. Establishment of the Skin Effect and Its Impediment to Fluid Flow in a Wellbore [J]. Petroleum English, 1953, 25 (8): 6-16.

