自立式钢制尾气烟囱设计与选型
兰洪强 张 毅 兰 林 刘萍萍 叶 桦 曹建强 王 泳 李广东
1.中国石油工程建设有限公司西南分公司, 四川 成都 610041;2.苏州云白环境设备制造有限公司, 江苏 苏州 215000
0 前言
随着人们环境保护意识的不断加强,经济和科学技术的发展越来越强调环境保护的重要性。工业烟囱作为石油石化行业和火电行业重要的尾气排放设备,其作用举足轻重。越来越严格的环保标准,以及越来越大型化的工业规模,促使工业烟囱朝着复杂化、大型化发展。较之传统的混凝土烟囱,钢制烟囱在一定程度上解决了混凝土烟囱腐蚀、老化的问题,并能更好地解决排烟的二次污染问题[1- 12]。钢结构的特性有利于定期检测和安全使用寿命的评估,除此之外,钢制烟囱结构在节约原材料、降低成本和缩短施工周期方面都具有很大的潜力,可靠性高,技术经济性更为合理[12- 13]。
天然气净化工业中,硫黄回收工艺是确保环保安全的重要技术,为满足环保要求,烟囱通常高度为90~120 m不等。经多级焚烧和余热回收的高温烟气通常含有NOx、SO2、SO3、H2S等产物[2],具有腐蚀性较强、介质温度高(300~650℃)和存在一定毒性(可能含微量H2S)的特点。传统做法采用钢制烟囱壳体内衬耐高温浇注料衬里,并以钢制塔架对烟囱筒体进行支撑,并由塔架承担地震和风载荷对烟囱的影响,确保烟囱的强度和稳定性。此法技术成熟可靠,但存在施工难度大,占地、造价等综合成本较高的缺点。随着自立式高耸构筑物的发展,工业用钢制烟囱已发展出多种不带辅助支撑的自立式结构。
本文结合调研成果、工程实践经验和分析计算,介绍了钢制尾气烟囱的结构选型原则和结构分析计算方法,综合考虑技术可靠性和经济合理性,为类似工程前期方案策划,提供参考和借鉴。
1 工艺介绍

中小规模的克劳斯装置尾气焚烧工艺通常采用直接热焚烧的方式,即在有过量空气存在的情况下,燃料气与空气燃烧后生成的烟气将尾气加热到一定温度,使其中的含硫化合物全部转化为SO2,焚烧产物经尾气烟囱排入大气中,见图1。该工艺适合于中小规模的克劳斯装置,排放的尾气温度一般在550~650℃。
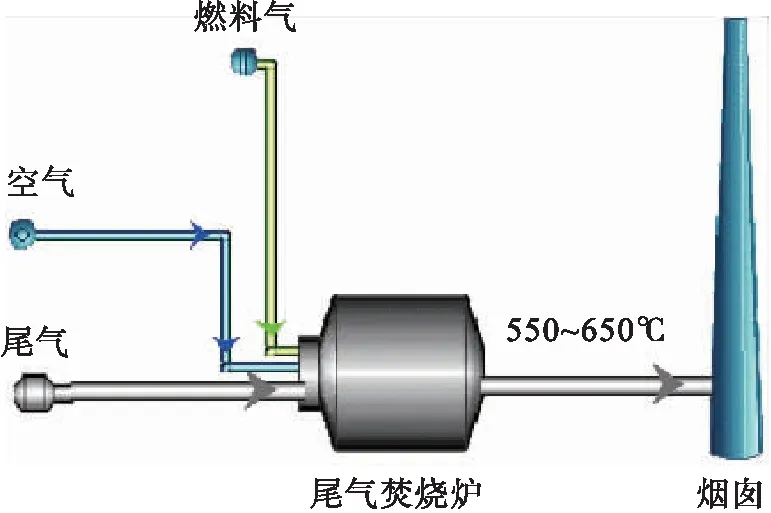
图1 尾气焚烧直接排放流程图
对于大型克劳斯装置,为降低能耗通常考虑在尾气焚烧炉后设置废热锅炉,利用回收的热量产生压力为3.5~4 MPa 的蒸气,并将尾气温度降低至300~350℃,见图2。
2 结构设计
2.1 常见结构形式
钢制烟囱作为高耸构筑物,从支撑结构类型上,主要分为拉索式、塔架式、自立式和集束式。
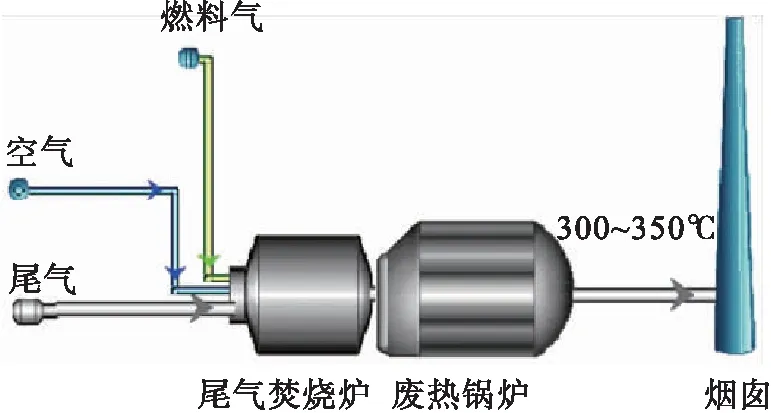
图2 尾气焚烧-回收余热后排放流程图
2.1.1 拉索式
拉索式在烟筒中上部位置采用均布斜拉钢索的结构,通过均布的预紧拉力传递到地面基础,使烟囱正常操作承受风载作用时保持稳定。由于拉索式结构属于预拉伸的柔性结构,基本无法承担地震载荷。此外,由于拉索需要与烟筒保持一定的角度,对于超过20 m的拉索式钢制烟囱,其地面基础结构分布占地区域面积大,随着烟囱的日趋大型化,钢制烟囱的安全性要求更高,用地需求更加紧张。拉索式支撑结构仅适用较小规模的设备[13- 15]。
2.1.2 塔架式
塔架式结构采用塔架钢结构形式,与设备筒体采用抱箍连接,形成整体式具有较高刚度的组合钢结构,可有效承担风载荷和地震载荷。其缺点是塔架结构地面基础部分占地面积相对较大,给用地紧张地区的工程实施带来一定的困难。塔架式烟囱适用于烟囱高度高,高径比(H/D)大,建造地区烟囱所受风载荷和地震载荷较大的项目。
根据国内外调研情况,结合国内实际现状,考虑安全性和经济性,120 m以上烟囱宜选用塔架式钢制结构。另外,在烟囱稳定性计算时,综合考虑结构安全性和技术经济合理性,应对塔架式烟囱和自立式烟囱进行综合技术经济对比[13-15]。
2.1.3 自立式
自立式钢制烟囱无需外部钢结构或辅助结构支撑,靠自身筒体刚度和强度,以及底座与基础的连接承担烟囱操作运行时的风载荷和地震载荷,筒体本身满足强度、刚度、挠度、振动和稳定性等要求,确保烟囱本体安全可靠[4]。
从国外烟囱理论和应用业绩看,自立式烟囱本体结构比非自立式烟囱结构尺寸和耗钢量大,但在综合占地指标上有绝对优势。且自立式结构简单,可实现工厂预制,现场组装、施工更为简便,已经成为国外众多工程应用的首选结构形式。自立式钢制烟囱由于计算模拟分析复杂,在国内尚未大规模推广和应用。
根据国外和国内自立式烟囱应用情况,目前高度不超过100 m的烟囱,采用自立式结构有较高的可行性。
2.1.4 集束式
集束式结构,即多根烟囱(烟筒)采用一定的几何结构形式排列,相互之间通过抱箍结构连接为一个整体,形成组合式结构,从而增加烟囱整体的刚度,满足设计条件下风载荷和地震载荷的要求。
集束式结构占地空间小,结构稳定可靠。缺点是适用范围窄,仅适用于多列装置或同类型装置,且对工艺装置的总图布置和对工艺配管的要求高。
2.2 理论依据
2.2.1 模态分析
模态分析是线性结构系统地震分析中最常用的方法。该方法通过计算一组正交向量之后,将大型整体平衡方程组缩减为数量相对较少的解耦的二阶微分方程,缩短用于数值求解这些方程的计算时间,并为结构静力分析和其他动力分析提供运算基础。
([K]-ω2[M]){φ}={0}
(1)
式(1)为结构振动的特征方程,模态分析就是计算该特征方程的特征值{ωi}(i=1,2,3,…,n),以及其对应的特征向量{φi}=(i=1,2,3,…,n),从而构成一个完备的模态集,描述其动力特性。
在实际工程设计中,为了减少计算量,通常取前6阶段分析结果[5]。
2.2.2 反应谱IMD分析
地震反应谱有力反应谱、位移反应谱、速度反加速度反应谱等,GB 50011-2001《建筑抗震设计规范》采用的是根据加速度反应谱得到的地震影响系数曲线,该影响系数取结构最大加速度响应与重力加速度的比值,以使该系数无量纲化。反应谱理论考虑了结构动力特性与地震动特性之间的动力关系,通过反应谱来计算由结构动力特性(自振周期、振型和阻尼)所产生的共振效应。地震时结构所受到的最大水平基底剪力,即总水平地震作用为:
FEK=kβ(T)G=α(T)G
(2)
式中:k为地震系数;β(T)=Sa(T)/a为加速度反应谱Sa(T)与地震动最大加速度a的比值,表示地震时结构振动加速度的放大倍数;G为结构等效重力载荷代表值;a(T)=kβ(T)为地震影响系数,是加速度反应谱Sa(T)与重力加速度g的比值,表示地震时由于振动加速度引起的地震力与等效重力荷载代表值的比值。
本文采用的反应谱通过软件生成,见图3。

图3 反应谱曲线
2.3 设计计算
2.3.1 建模
单筒式烟囱和套筒式烟囱从结构支撑类型上无本质区别,分析方法相同,套筒式烟囱的内筒除自身重力以外不考虑其他载荷,主要支撑由外筒承担。因此在进行分析时均按照单筒考虑,建立模型。
针对某工程的钢制烟囱,采用LUSAS商业软件,建立模态分析模型,该钢制烟囱的结构形式为自立式钢制烟囱,总体高度为90 m,分为3个变径段,底座为地脚螺栓连接。具体结构建见图4~5。
计算满足如下假定条件:
1)材料为连续均匀各向同性。
2)分析始终假定整个模型保持在材料的弹性限度之内。
3)采用三维实体元素建模和分析,以便更详细评估这些应力。
2.3.2 地震分析
根据模态分析的结果和生成的反应谱进行动力分析。对于自立式钢制烟囱,竖向加速度引起的作用于烟囱横截面的纵向力计算容易,因此对于模型应力分析暂不考虑竖向加速度的影响,简化模型加载情况,简化计算。因此只分析平面内X、Y方向的作用力与反力和相关的位移[16-19]。

图4 自立式钢制烟囱结构图

图5 自立式钢制烟囱有限元整体模型
根据规范和烟囱实际工程资料,确定工程所在地的地震设防烈度、建筑类别、类场地土类别和设计地震分组、特征周期、地震影响系数、结构阻尼比ξ,计算得到相关的反应谱曲线,见图3。
2.3.3 风载荷分析
由于烟囱近似于一端固支的长柔杆结构,与其他类型的结构比较,钢制烟囱的水平荷载引起的结构反应特别强烈。在各类载荷中,风载荷对烟囱结构是最重要的,不仅结构应力的大部分是风载荷引起的,而且烟囱结构振动控制的动力源也是风载荷。
因此,钢制烟囱设计时要求结构在强风下不会发生破坏、倒塌、开裂、局部失稳、存在残余变形。在脉动风载荷作用(包括顺风向、横风向旋涡干扰力)下,会引起烟囱结构的振动反应(包括动内力、动位移、振动加速度)。其振动反应与结构本身的动力特性有关,结构的材料性质、质量分布、结构刚度和结构形式都将影响结构的动力特性。风载荷确定则与烟囱结构的自振频率(周期)、各阶振型等有着密切的联系。
根据《建筑结构荷载规范》垂直于建筑表面上的风载荷标准值,应按以下公式计算:
Wk=βkμsμkWo
(3)
式中:Wk为风载荷标准值,kN/m2;βk为高度Z处的风振系数;μs为风载荷体型系数;μk为风压高度变化系数;Wo为基本风压,kPa。
根据本文研究烟囱的所在地,风压取值为0.4 kPa。
顺风力作用下,顺风向和横向风产生响应。横风力作用下,由于漩涡形成的情况不同,结构受力情况也不同。
2.3.4 分析结果
2.3.4.1 模态分析结果
本模型模态分析,一共输入20阶,取前6阶的结果分析。高阶振动出现竖向振动,对于这类型的结构竖向振动表现不明显,因此暂不考虑。模态分析结果见表1。
表1前6阶模态分析结果

阶次周期T/s频率f/Hz11.4270.70121.3140.76130.3053.27540.3053.27750.1228.16660.1228.166
从模态分析结果看出:主体结构第1阶固有频率为f=0.707 Hz,T1=1.427 S,基本周期适中,说明结构横向刚度比较合理。T2/T1=0.921,结构纵横两向周期比较接近,说明结构两方向刚度均匀,抗震性能较好[6]。
2.3.4.2 综合工况分析结果
经过计算分析,获得钢制烟囱在自重、风载、温度等载荷下的应力和相关的位移,见图6和表2,结果符合GB 50051-2013《烟囱设计规范》要求(以下简称GB 50051-2013)。


图6 最大应力和相关的位移
表2应力分析结果

项目应力max/MPa应力min/MPa位移/mmGB50051-2013位移规定值/mm结果29.98-49.97114.34L/100=200
3 推荐选型
3.1 基本原则
自立式钢制烟囱从筒体结构类型可分为单筒式和套筒式。
单筒式烟囱和套筒式烟囱从结构支撑类型上无本质区别,皆可使用上述支撑结构类型。套筒式烟囱相比单筒式烟囱更便于解决温度和腐蚀问题。应针对不同的烟气温度工况和腐蚀特性,选取合适的筒体结构,兼顾安全性和经济性。可对不同烟气工况进行分类,以便于筒体结构选型。温度工况和腐蚀特性不同导致选型不一致时需采用更安全的筒体结构类型。
3.2 温度工况选型
不同介质温度下推荐的结构形式见表3。
表3不同介质温度下推荐结构形式

烟气温度/℃主要腐蚀风险防腐保温形式衬里保温套筒60≤t<150露点腐蚀◇/★150≤t<350露点腐蚀+高温烟气腐蚀☆◇★350≤t<600高温烟气腐蚀☆/★600≤t高温烟气腐蚀★/☆ 注:★为优选形式;☆为次优选形式;◇为可选形式。
应注意以下几点:
1)烟气温度60℃≤t<150℃时,主要腐蚀风险是露点腐蚀,因此钢制烟囱应针对露点腐蚀采取相应措施。优选方案可采取耐蚀合金内套筒式结构,也可采用内衬里(含防腐涂料)的措施。采用外保温的形式解决不了酸气露点腐蚀,因此不应采用。
2)烟气温度150℃≤t<350℃时,主要腐蚀风险介于酸气露点腐蚀和高温硫化腐蚀之间,腐蚀类型对温度参数的变化敏感,腐蚀机理复杂,应进行精确的传热计算,同时为保证设备长周期安全运行,推荐采用套筒式结构,兼顾设备强度和稳定性,其耐高温和耐腐蚀性能俱佳;推荐采用内衬里结构形式,辅以防腐涂料,工程应用经验表明可靠性较高;外保温形式作为可选项,需结合精确的传热计算,确保烟筒壁面金属壁温高于介质露点温度;由于保温结构工程量大,施工难度高,如有缺陷,将导致保温层在雨雪气候中失效,从而导致金属壁温偏离设计值,引起严重腐蚀。
3)烟气温度350℃≤t<650℃时,主要腐蚀风险为高温烟气腐蚀,因此采用套筒式结构和衬里式结构,都可以很好地避免碳钢筒体与高温烟气介质的直接接触。其中套筒式结构完全杜绝碳钢外筒体的腐蚀风险,施工质量高的衬里结构则可以大大降低腐蚀风险。保温结构因不能解决金属壁温过高以及碳钢金属材料特性变化的问题,因此不予推荐。
4)烟气温度650℃≤t时,主要腐蚀风险为高温烟气腐蚀。由于套筒式结构,需要耐高温性能更好的耐蚀合金作为内筒,其材料成本较高,但作为技术方案,为可选方案。采用隔热衬里结构,可以很好地解决耐高温的问题,但由于温度过高引起的衬里层过厚,导致衬里层垮塌等失效的风险也是存在的。因此,建议超过650℃的尾气系统,从工艺上尽量考虑余热回收,从而降低烟气温度。
3.3 腐蚀特性选型
导致烟气腐蚀性的原因有腐蚀介质、烟气温度、烟气湿度、烟气流速等。钢制烟囱腐蚀性选型应针对具体案例,界定腐蚀机理,选取适宜的防腐内衬。对于筒体结构在腐蚀特性影响下只做大类划分。
1)微腐蚀,常规为烟温150~300℃,腐蚀介质含量低,可选用单筒式或套筒式。
2)中度腐蚀,常规为烟温小于150℃,有一定腐蚀介质,宜选用套筒式。
3)强腐蚀,常规为烟温小于100℃,腐蚀介质含量高,烟气湿度大或烟气温度高于450℃,腐蚀介质含量高,应选用套筒式。
4 结论
通过以上分析,自立式钢制烟囱在各种综合载荷下应力、位移值均在规范允许的范围内,钢烟囱结构在节约原材料、降低成本和缩短施工周期方面都具有很大的潜力,应用于实际工程中具有经济性、安全可靠性等优势。
参考文献:
[1] 马殿晖.钢制烟囱的机械设计[J].黑龙江科技信息,2008,14(5):21.
Ma Dianhui. Mechanical Design of Steel Chimneys [J]. Heilongjiang Science and Technology Information, 2008, 14 (5): 21.
[2] 陈赓良.硫黄回收尾气处理工艺的技术发展动向[J].天然气与石油,2016,34(3):35-36.
Chen Gengliang. Development Trend of Techniques for Sulfur Recovery Tail Gas Treatment Process [J]. Natural Gas and Oil, 2016, 34 (3): 35-36.
[3] 李建波.基于有限元的自立式钢烟囱结构稳定性分析[J].建筑技术开发,2013,40(4):1-3.
Li Jianbo. Stability Analysis of Self-supporting Steel Chimney Based on Fem [J]. Building Technique Development, 2013, 40 (4): 1-3.
[4] 王 忠.美国烟囱钢套筒的设计方法与规定(一)[J].电力建设,1992,13(1):31-33.
Wang Zhong. Design Methods and Regulations of American Chimney Steel Sleeve(Ⅰ)[J]. Electric Power Construction, 1992, 13 (1): 31-33.
[5] 刘 季,何立民.烟囱在水平与竖向地震动联合作用下的反应[J].地震工程与工程振动,1983,3(2):89-90.
Liu Ji, He Limin. Analysis Seismic Respense of Chimneys to Combined Horizontal and Vertical Ground Motion [J]. Earthquake Engineering and Engineering Vibration, 1983, 3 (2): 89-90.
[6] 董启明,龚景海,陈 锋,等.超高双筒钢烟囱体系研究[J].钢结构,2010,25(4):17-19.
Dong Qiming, Gong Jinghai, Chen Feng, et al. Research on Superhigh Steel Chimney of Dual-Tube System [J]. Steel Construction, 2010, 25 (4): 17-19.
[7] 中国电力规划设计协会.火力发电厂设计技术规程:DL/T 5000-2000[S].北京:中国标准出版社,2001.
China Electric Power Planning & Engineering Association.Technical Code for Designing Fossil Fuel Power Plants: DL/T 5000-2000[S]Beijing: China Standard Press, 2001.
[8] Ciesielski R, Gaczek M, Kawecki J. Observation Results of Cross-wind Response of Towers and Steel Chimneys [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43 (3): 2205-2211.
[9] 温德超,刘季林,王清刚.80 m高钢烟囱的风振分析[J].工程抗震,2004,(1):26-29.
Wen Dechao, Liu Jilin, Wang Qinggang. Wind Vibration Analysis of a 80 m Tall Steel Chimney [J]. Earthquake Resistant Engineering, 2004, (1): 26-29.
[10] 牛春良.烟囱横向风振计算[J].特种结构,2004,21(3):60-62.
Niu Chunliang. The Calculation of Chimney Across-wind Sympathetic Vibration [J]. Special Structures, 2004, 21 (3): 60-62.
[11] 崇惠萍.钢烟囱横风向风振的防止[J].江苏工业学院学报,2004,16(1):21-24.
Chong Huiping. Prevention of Steel Stacks from Crosswind Vibration [J]. Journal of Jiangsu Polytechnic University, 2004, 16 (1): 21-24.
[12] 魏利金.套管式多管烟囱结构设计[J].工程建设与设计,2007,(8):22-26.
Wei Lijin. Canular Multibulb Chimney Structure Design [J]. Construction & Design for Project, 2007, (8): 22-26.
[13] 王建强,蔡震旦.某钢烟囱的风振分析[J].特种结构,2006,23(3):90-92.
Wang Jianqiang, Cai Zhendan. Wind Vibration Analysis of a Steel Chimney [J]. Special Structures,2006,23(3):90-92.
[14] 朱 彤,周 晶,林 皋,等.烟囱模型动力试验研究[J].世界地震工程,2007,23(3):113-119.
Zhu Tong, Zhou Jing, Lin Gao, et al. Research on Dynamic Structural Model Tests of Chimneys [J]. World Earthquake Engineering, 2007, 23 (3): 113-119.
[15] 王学民,方伟定,方鸿强,等.基于性能的烟囱抗震设计[J].工业建筑,2007,37(增刊1):1159-1163.
Wang Xueming, Fang Weiding, Fang Hongqiang, et al. Performance-based Seismic Design of the Chimney [J]. Industrial Construction, 2007, 37 (Suppl 1): 1159-1163.
[16] 丁世文,王云剑,周四骏.烟囱模型竖向冲击振动破坏试验研究[J].地震工程与工程振动,1999,19(3):34-36.
Ding Shiwen, Wang Yunjian, Zhou Sijun. Fracture Test of Chimney Models Subjected to Vertical Shock [J]. Earthquake Engineering and Engineering Vibration, 1999, 19 (3): 34-36.
[17] 任耀辉.烟囱竖向地震作用下抗震性能分析[D].西安:西安建筑科技大学,2008.
Ren Yaohui. The Seismic Behavior of Chimney Under Vertical Earthquake Action [D]. Xi’an: Xi’an University of Architecture and Technology, 2008.
[18] 张化振,刘广立,胡长明,等.某钢烟囱塔架结构的优化设计[J].钢结构,2008,23(7):23-25.
Zhang Huazhen, Liu Guangli, Hu Changming, et al. Structural Optimum Design of a Steel Chimney Tower [J]. Steel Construction, 2008, 23 (7): 23-25.
[19] 苏国柱,王永焕,徐海翔,等.异型高耸塔架结构优化设计[J].工业建筑,2005,35(2):57-68.
Su Guozhu, Wang Yonghuan, Xu Haixiang, et al. Structural Optimum Design of Allotype High Tower [J]. Industrial Construction, 2005, 35 (2): 57-68.

