Monte Carlo方法在管道裂纹缺陷评价中的应用
李星雨 杨玉锋 魏立新 张华兵 刘 鹏 王 力 张 煜
1.东北石油大学石油工程学院, 黑龙江 大庆 163118;2.中国石油管道科技研究中心/油气管道输送安全国家工程实验室, 河北 廊坊 065000
0 前言
管道内检测(In-Line Inspection,ILI)可直接检测出油气管道可能存在的管体裂纹缺陷,而且检测时不影响油气管道的正常输送。三轴漏磁内检测技术的发展,使得管道裂纹的检测和尺寸量化成为可能[1-3]。国内长输油(气)管道在制造、施工过程中管体会产生大量裂纹缺陷。如某输气管道经过三轴漏磁内检测后检测出大量管道管体裂纹缺陷,经开挖验证取样分析,这些裂纹缺陷基本上属于焊接裂纹、热处理裂纹和应力裂纹。根据英国标准BS 7910:2013《金属结构缺陷可接受性评价指南》[4](以下简称BS 7910:2013),对此类缺陷进行结构完整性评价可将其视为平面缺陷。然而三轴漏磁内检测对管道裂纹缺陷的尺寸量化技术尚不成熟,量化后的缺陷尺寸无法达到百分之百准确,具有较大的不确定性,而且管材自身参数也存在较大不确定性(如断裂韧性、屈服强度)。传统的确定性评价仅给出缺陷是否可以接受的确定性结论,而无法对管体裂纹缺陷的失效可能性做出定量评估。需要研究基于可靠性的结构完整性评价方法,以便更好地对管道的失效风险进行评估,制定经济、合理的维修维护方案。
1 结构可靠性分析
结构可靠性分析[5-7](Structural-Reliability Analysis,SRA)是一种基于可靠性的结构完整性评价方法,是一种结构系统的安全评价方法。其主要内容是为了评定结构在规定的使用条件及服役时间内,完成预期功能而不失效的能力,进而为制定维修维护策略提供重要理论依据。和传统的使用安全系数的确定性评价相比,结构可靠性分析使用概率和数理统计理论对系统的不确定性因素及参数波动进行处理,克服了由几何尺寸、材料性能及其运行状态等变量参数的不确定性导致无法准确评价结构安全状态的问题,评价结果更加客观可信。
对于已确定缺陷类型的结构而言,其可靠性评价可分为四个主要步骤,具体流程见图1。

图1 基于可靠性的含缺陷结构完整性评价流程
其中,整个评价流程的核心是求解缺陷的失效概率,它对于结构安全性和可靠性的准确评价以及评价结果在工程实际中的应用有重要意义,因此一直是结构可靠性评价中关注的焦点问题。目前,国内外常用的概率求解方法包括直接积分法[8-10]、分项系数法[11-12]及Monte Carlo模拟法[13-18]等。相比而言,直接积分法在参数较多时计算繁琐复杂,不易实现;分项系数法需要考虑各项参数的分项安全系数,往往导致评价结果过于保守;而Monte Carlo模拟法是以概率和统计理论为基础的一种计算方法,能够比较逼真地描述具有随机性质的事物特点,不仅精确程度高,而且程序结构简单,易于实现计算机批量处理。本文采用Monte Carlo模拟法对管道裂纹缺陷进行失效概率求解,通过与目前使用的确定性评价方法进行对比,提出一种对含有裂纹缺陷的管道结构完整性评价的新思路。
2 管道裂纹缺陷确定性评价
2.1 评价方法

图2 BS 7910:2013中2 A级评价失效评估图

(1)
式中:Kr为断裂力学变量,无量纲;Lr为载荷比,无量纲。
2.2 评价参数选择
管道裂纹缺陷分三种:内表面、外表面和内嵌缺陷。目前,三轴漏磁内检测技术可以识别出管道管体裂纹缺陷并进行尺寸量化,但无法识别缺陷在裂纹厚度中的具体位置以及缺陷的具体种类。由于表面缺陷通常比同样几何尺寸的内嵌缺陷更加危险,同时考虑到管道管体裂纹缺陷的性质,出于保守性原则将内检测报告的管体裂纹缺陷作为内表面裂纹缺陷,使用英国标准BS 7910:2013中2 A级评价路线进行评价。

英国标准BS 7910:2013的附录K中出于对评价参数不确定性的考虑,给出了不同条件下的分项安全系数建议值。本文分别对是否考虑分项安全系数的两种情况进行了计算。各分项安全系数的建议值按照将管道作为该附录中的“无备份组件”和“失效后果中等”来选取,变异系数(Coefficient Of Variation,COV)取0.1。
确定性评价参数选取见表1。
表1确定性评价参数
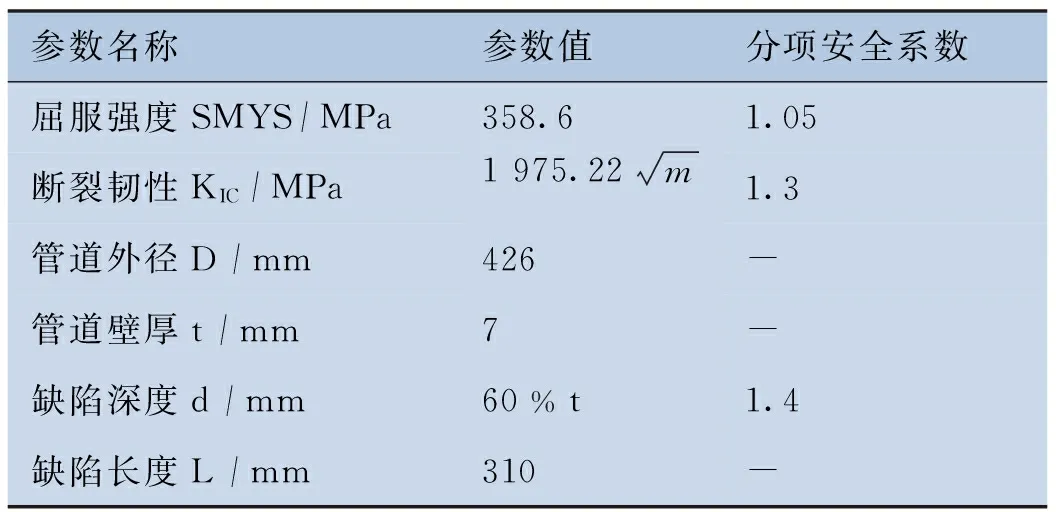
参数名称参数值分项安全系数屈服强度SMYS/MPa358.61.05断裂韧性KIC/MPa1975.22m1.3管道外径D/mm426-管道壁厚t/mm7-缺陷深度d/mm60%t1.4缺陷长度L/mm310-
2.3 评价结果
该输气管道管体裂纹缺陷的2 A级确定性评价结果见图3。
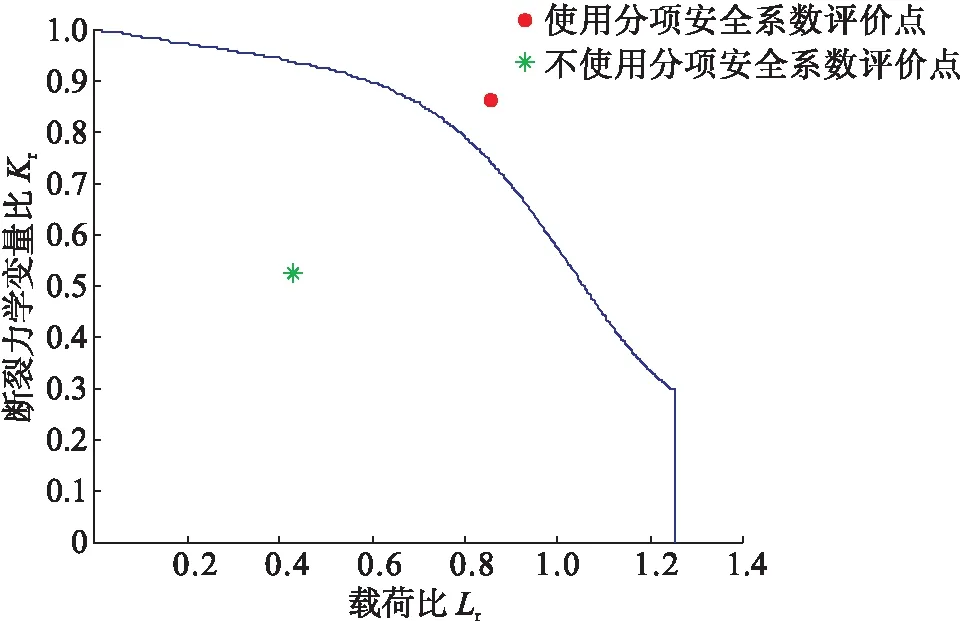
图3 2 A级确定性评价结果
由图3可知,在使用分项安全系数时处于不可接受区域,而不考虑分项安全系数的情况下该缺陷处于可接受区域,且计算出的Lr和Kr结果相差较大。可以看出安全系数的选取与否对确定性评价方法的评价结果具有很大影响,同时确定性评价方法又仅仅给出缺陷是否可接受的结论,无法对缺陷失效的可能性进行定量评估,因此有必要开展管体缺陷可靠性评价的研究。
3 管体裂纹缺陷的可靠性评价
3.1 Monte Carlo模拟
对管体裂纹缺陷的失效可能性大小进行定量评价,应用蒙特卡洛(Monte Carlo)模拟抽样对失效概率进行估算。在模拟过程中,将管材的屈服强度、断裂韧性以及缺陷的深度、长度作为服从各自对应分布的随机变量,生成一组随机参数后计算缺陷的载荷比Lr和断裂力学变量比Kr,以2 A级评价失效评估图作为评价指标进行可接受性评价。因此,估计失效概率P(f)可以通过式(2)求出:
P(f)=N/M
(2)
式中:N为判定为不可接受的次数,次;M为蒙特卡洛模拟的总试验次数,次。
当模拟抽样试验次数越大时,失效概率的估计值越趋近于失效概率的真实值。
3.2 评价参数分布的确定
金属材料结构完整性评价的参数分布概率可参考Pluvinage G[19]的总结,Pluvinage G认为变异系数是衡量材料属性分布离散程度的最优参数。对于低碳钢产品,屈服强度、抗拉强度和断裂韧性的变异系数,均可以取0.1。

3.3 失效概率
图4分别给出了模拟次数为104、105、106、107次时,使用Matlab软件进行Monte Carlo模拟法的计算结果。其中分别有38、338、3 160、31 702次缺陷评价点处于不可接受区域,表3给出了4种模拟抽样次数的失效概率。随着模拟次数的增加,失效概率趋于一个稳定值,模拟次数为107次时,该输气管道管体裂纹缺陷的估计失效概率为3.17×10-3,见图5。
表2评价参数分布及取值
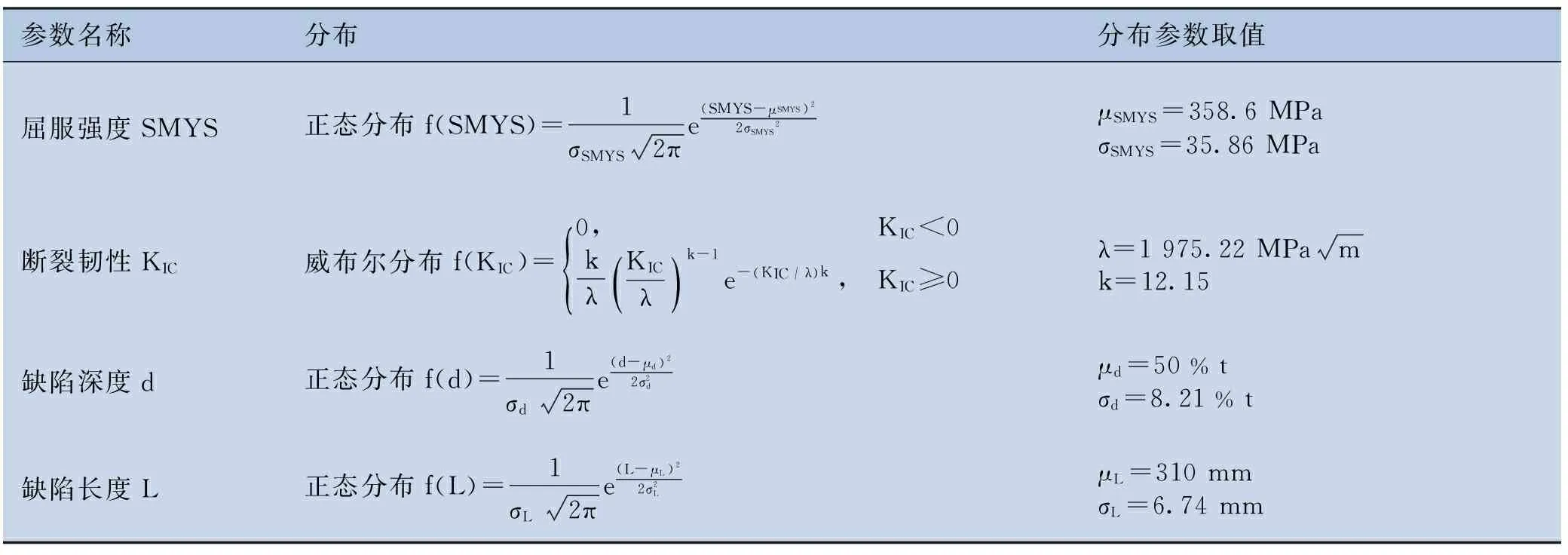
参数名称分布分布参数取值屈服强度SMYS正态分布f(SMYS)=1σSMYS2πe(SMYS-μSMYS)22σSMYS2μSMYS=358.6MPaσSMYS=35.86MPa断裂韧性KIC威布尔分布f(KIC)=0,KIC<0kλKICλ()k-1e-(KIC/λ)k,KIC≥0{λ=1975.22MPamk=12.15缺陷深度d正态分布f(d)=1σd2πe(d-μd)22σ2dμd=50%tσd=8.21%t缺陷长度L正态分布f(L)=1σL2πe(L-μL)22σ2LμL=310mmσL=6.74mm
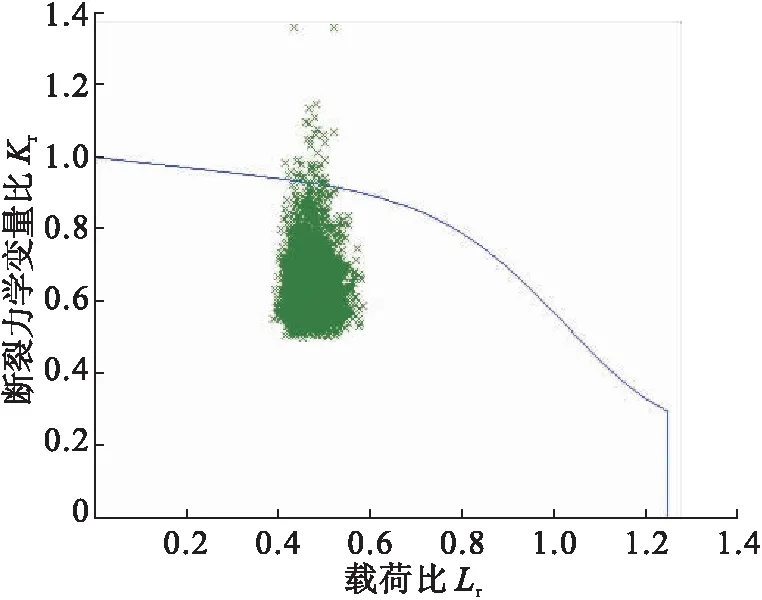
a)模拟次数为104次结果
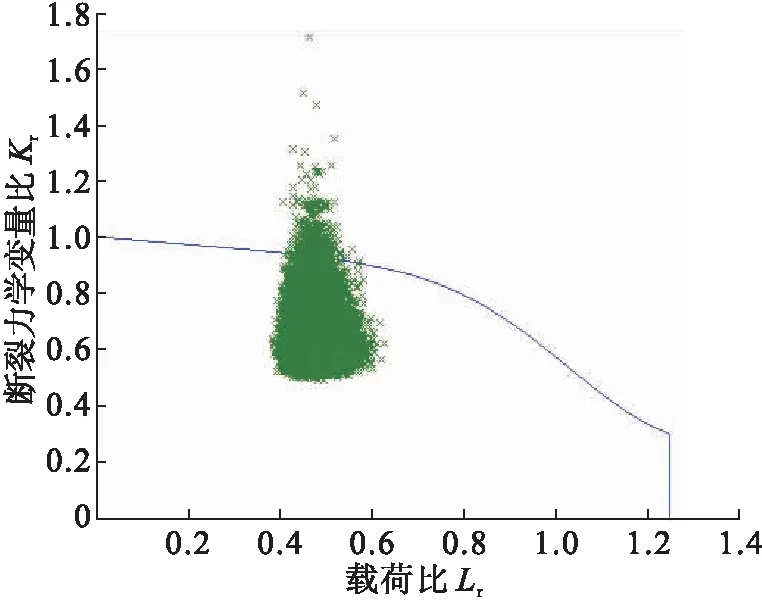
b)模拟次数为105次结果

c)模拟次数为106次结果
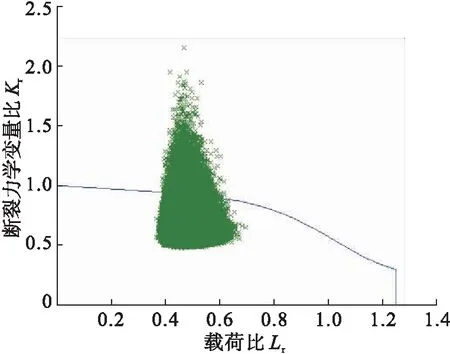
d)模拟次数为107次结果
表3不同模拟次数下的估计失效概率计算结果

模拟次数M/次估计失效概率P(f)/(×10-3)1043.801053.381063.161073.17

图5 不同模拟次数下的失效概率结果
表4其他典型尺寸的裂纹缺陷失效概率
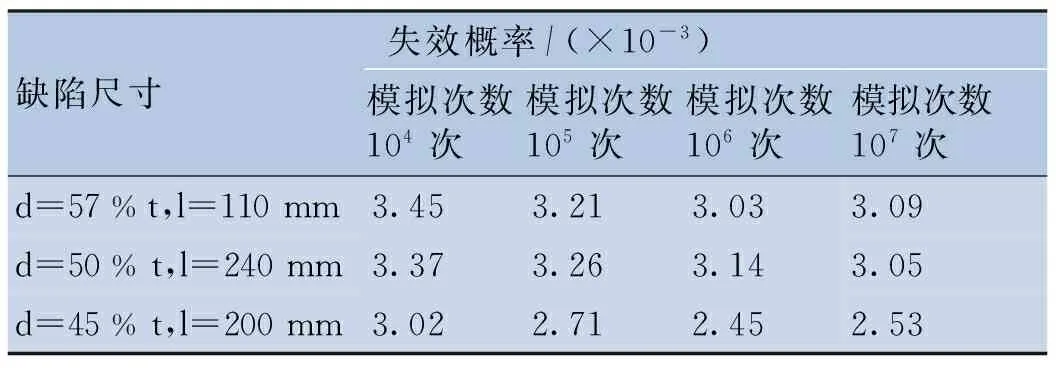
缺陷尺寸失效概率/(×10-3)模拟次数104次模拟次数105次模拟次数106次模拟次数107次d=57%t,l=110mm3.453.213.033.09d=50%t,l=240mm3.373.263.143.05d=45%t,l=200mm3.022.712.452.53

3.4 敏感性分析

β=ΔP(f)/ΔCOV
(3)
用Monte Carlo模拟法进行敏感性分析计算,分别求出其他参数不变,另一个参数的变异系数增加0.1时的失效概率,所得敏感性分析结果见表5。
从表中可知,对失效概率的影响程度缺陷深度最大,断裂韧性次之,屈服强度再次,缺陷长度最小。结果说明:失效概率受缺陷深度的影响最大,提高内检测中缺陷深度的尺寸量化精度对于准确评估缺陷的严重程度具有重要的意义。
表5敏感性分析结果

参数名称变异数增量ΔCOV失效率增量ΔP(f)敏感性系数β屈服强度SMYS0.12.20×10-32.20×10-2断裂韧性KIC0.17.40×10-37.40×10-2缺陷深度d0.14.30×10-24.30×10-1缺陷长度L0.14.07×10-44.07×10-3
4 可靠性评价与确定性评价结果比较
确定性评价方法的结果受参数不确定性和分项安全系数选择的影响较大,而且确定性评价仅能得到缺陷是否可接受的单一结论。而应用Monte Carlo模拟的可靠性分析评价可以定量给出含缺陷结构的失效概率。根据管道内检测报告的大量管体裂纹缺陷,管道管理部门需要权衡管道失效风险和维修维护费用,制定相应的风险可接受标准,及时作出合理的维修维护决策。因此,基于可靠性的结构完整性评价相对来说就更具有指导意义,更具有实际应用价值。
5 结论
1)基于Monte Carlo模拟法可靠性分析结构完整性评价可以对油气管道管体裂纹缺陷定量评价分析,能定量计算出缺陷管道的失效概率。对影响因素的敏感性分析,能够评估各影响因素对失效概率影响程度的大小。
2)与确定性评价方法相比,基于可靠性分析的结构完整性评价方法更便于管道管理部门权衡管道失效风险和维修维护费用,对及时作出合理的维修维护决策更具有指导意义。
3)基于Monte Carlo模拟的可靠性分析,计算管体裂纹缺陷的失效概率可作为英国标准BS 7910:2013在评价管体裂纹缺陷的补充内容。
参考文献:
[1] 冯庆善,张海亮,王春明,等.三轴高清漏磁检测技术优势及应用现状[J].油气储运,2016,35(10):1050-1054.
Feng Qingshan, Zhang Hailiang, Wang Chunming, et al. Advantages of Three-Axial High-Resolution Magnetic Flux Leakage Inspection Technology and Its Application Status [J]. Oil & Gas Storage and Transportation, 2016, 35 (10): 1050-1054.
[2] 丁建林.我国油气管道技术和发展趋势[J].油气储运,2003,22(9):22-25.
Ding Jianlin. China’s Oil and Gas Pipeline Technology and Its Development Current [J]. Oil & Gas Storage and Transportation, 2003, 22 (9): 22-25.
[3] 冯庆善.在役管道三轴高清漏磁内检测技术[J].油气储运,2009,28(10):72-75.
Feng Qingshan. Three-Axis High-Resolution MFL Internal Inspection Technology for In-Service Pipeline [J]. Oil & Gas Storage and Transportation, 2009, 28 (10): 72-75.
[4] British Standards Institution. Guide on Methods for Assessing the Acceptability of Flaws in Metallic Structures: BS-7910[S]. London: British Standards Institution, 2013.
[5] Ditlevsen O, Madsen H O. Structural Reliability Methods [M]. Chichester: John Wiley & Sons Ltd, 1996.
[6] 高 建,何仁洋,王德国.基于可靠性分析的大跨度跨越管桥寿命预测[J].油气储运,2010,29(5):350-353.
Gao Jian, He Renyang, Wang Deguo. Service Life Prediction for Longspan Overhead Crossing Pipe Bridge Based on Reliability Analysis [J]. Oil & Gas Storage and Transportation, 2010, 29 (5): 350-353.
[7] 陈 健,汤 怡,孙 雷,等.某河底穿越管道环焊缝缺陷的安全评价[J].油气储运,2014,33(11):1222-1224.
Chen Jian, Tang Yi, Sun Lei, et al. Safety Evaluation of Girth Weld Defect of a River Bottom Crossing Pipeline [J]. Oil & Gas Storage and Transportation, 2014, 33 (11): 1222-1224.
[8] 苏 欣,杨 君,袁宗明,等.腐蚀管道的可靠性评价[J].石油工程建设,2005,31(6):9-12.
Su Xin, Yang Jun, Yuan Zongming, et al. Reliability Assessment of Corrosion Pipeline [J]. Petroleum Engineering Construction, 2005, 31 (6): 9-12.
[9] 熊昕东,陈利琼,刘 坤.腐蚀管道剩余强度可靠性评估[J].河南石油,2004,18(3):61-62.
Xiong Xindong, Chen Liqiong, Liu Kun. Reliability Assessment of Residual Strength of Corroded Pipelines [J]. Henan Petroleum, 2004, 18 (3): 61-62.
[10] 刘惟信.机械可靠性[M].北京:清华大学出版社,1996.
Liu Weixin. Mechanical Reliability [M]. Beijing: Tsinghua University Press, 1996.
[11] 刘 敏,霍立兴,张玉凤.含缺陷焊接压力容器和管道概率安全评定的分项系数方法[J].焊接,1999,(8):12-14.
Liu Min, Huo Lixing, Zhang Yufeng. Partial Factor Method for Probability Safety Assessment of Welded Pressure Vessels and Pipes with Cracks [J]. Welding & Joining, 1999, (8): 12-14.
[12] 樊 恒,闫相祯,冯耀荣,等.基于分项系数法的套管实用可靠度设计方法[J].石油学报,2016,37(6):807-814.
Fan Heng, Yan Xiangzhen, Feng Yaorong, et al. Practical Reliability Design Method of Casing Based on Partial Coefficient Method [J]. Acta Petrolei Sinica, 2016, 37 (6): 807-814.
[13] Alamilla J L, León D D, Flores O. Reliability Based Integrity Assessment of Steel Pipelines under Corrosion [J]. Corrosion Engineering, Science and Technology, 2005, 40 (1): 69-74.
[14] Lee O, Kim D H, Park Y C. Reliability of Structures by Using Probability and Fatigue Theories [J]. Journal of Mechanical Science and Technology, 2008, 22 (4): 672-682.
[15] 王 侨,谢禹钧,龚 雪.基于蒙特卡罗法管道失效概率的计算[J].辽宁石油化工大学学报,2012,32(2):67-69.
Wang Qiao, Xie Yujun, Gong Xue. Calculation of Pipe Failure Probability Based on Monte Carlo Method [J]. Journal of Liaoning University of Petroleum & Chemical Technology, 2012, 32 (2): 67-69.
[16] Binder K. Monte-Carlo Methods in Statistical Physics [M]. New York: Springer-Verlag, Berlin Heideberg, 1986: 71-82.
[17] 燕秀发,谢禹钧,戴 耀,等.基于概率断裂力学的管道失效分析[J].机械设计,2004,21(11):35-38.
Yan Xiufa, Xie Yujun, Dai Yao, et al. Pipeline Failure Analysis Based on Probabilistic Fracture Mechanics [J]. Journal of Machine Design, 2004, 21 (11): 35-38.
[18] 温 凯,张文伟,宫 敬,等.天然气管道可靠性的计算方法[J].油气储运,2014,33(7):729-733.
Wen Kai, Zhang Wenwei, Gong Jing, et al. Computation of Gas Pipeline Reliability [J]. Oil & Gas Storage and Transportation, 2014, 33 (7): 729-733.
[19] Pluvinage G. Safe and Reliable Design Methods for Metallic Components and Structures Design Methods [M]. Berlin: Springer Netherlands, 2009: 175-207.
[20] Zhang G L, Luo J H, Zhao X W, et al. Research on Probabilistic Assessment Method Based on the Corroded Pipeline Assessment Criteria [J]. International Journal of Pressure Vessels and Piping, 2012, 95: 1-6.
[21] 蔡 毅,邢 岩,胡 丹,等.敏感性分析综述[J].北京师范大学学报:自然科学版,2008,44(1):9-16.
Cai Yi, Xing Yan, Hu Dan, et al. On Sensitivity Analysis [J]. Journal of Beijing Normal University: Natural Science, 2008, 44 (1): 9-16.

