V形肋条减阻技术在输气管道中的数值研究
唐绍猛
山西天然气有限公司规划技术部, 山西 太原 030032
0 前言
目前,中国天然气产业已进入高速发展期,具有广阔的发展前景。由于天然气流速快、压力高,天然气管道几乎都运行在阻力平方区域内[1],在此区域内的流体流动摩阻系数只与管壁粗糙度有关。因此,降低管道输送阻力对于提高管道输送效率具有重要意义[2]。目前,输气管道的减阻方法主要有三种:内涂层减阻法[3]、减阻剂减阻法[3]和界面仿生减阻法[4]。但内涂层减阻法[2]不适用于管径500 mm以上的输气管道,并且在管道快速泄压和清管等外力作用下会使涂层出现起泡、剥离现象;减阻剂减阻法目前在实验室小口径环道测试中应用,可靠性尚需验证和改进,而且尚未有大口径管道实验相关报道;而仿生非光滑表面减阻法是借鉴仿生学研究理论,把物体表面加工成非光滑形态,进而改变表面边界层流场结构,抑制湍流猝发频率和强度,降低表面摩擦阻力。此类减阻技术不需要添加特殊设备,且不会造成额外的能源消耗,故具有极高的科研意义和应用前景。

肋条的尺寸由肋条高度以及肋条间距确定,通常用无量纲化表示,即无量纲肋高度h+和无量纲肋间距s+,满足公式(1)和(2):
(1)
(2)
式中:h+为肋高度,无量纲;s+为肋间距,无量纲;h为肋高度,m;s为肋条间距,m;U∞为流速,m/s;ν运动黏度,m2/s;Cf为阻力系数,无量纲。

以小管径输气管道(φ=25 mm)为研究对象,如计算整个圆管内的肋条,肋条数量较多,网格数量较大,因此仅计算圆管的一部分肋条,以周期性边界给出,这样可以达到减少网格的计算量,同时提高计算效率,来分析肋条在小管径输气管中的减阻和流动状况,并与大管径输气管道(φ=1 219 mm)进行对比,把大管径输气管道上进行仿生肋条的数值模拟近似转化为光滑平板上增加肋条的输气管道数值模拟[20]。
1 数值模拟
1.1 计算域及边界条件
流向长度为2 m,保证湍流充分发展,圆管的公称直径为25 mm。进口处为速度入口,出口为自由流出口,壁面为无滑移壁面,肋条部分为旋转周期性边界条件。图1为计算域网格和切平面网格,轴向方向网格节点均匀分布,径向方向在靠近管壁处进行了网格加密,并进行网格无关性验证。
1.2 工质的选取
研究对象为天然气,采用fluent自带材料数据库中CH4进行数值模拟。T=288.16 K,ρ=0.667 9 kg/m3,μ=1.087×10-5kg/m·s。
1.3 肋条几何尺寸
由于输气管道的公称直径较小,选取具有最佳减阻效果的对称V形肋条[21-22]进行数值模拟,对称V形肋条输气管道的几何尺寸取h=s=0.51 mm以及h=s=0.9 mm[21]。

a)计算域网格

b)切平面网格
1.4 模拟参数设置
采用重整化RNG(重整化群湍流模型)的增强壁面函数湍流模型进行数值模拟,可以得到较准确的模拟结果。离散格式采用二阶迎风格式,具有一定的稳定性并具有较高的精度。流场的迭代求解方法为SIMPLEC算法,具有较快的收敛速度,其残差精度为10-6。
1.5 流动参数
城市燃气管道多为低压管道,流速较小,流速范围为2.5~12.5 m/s。流动参数见表1。
表1流动参数
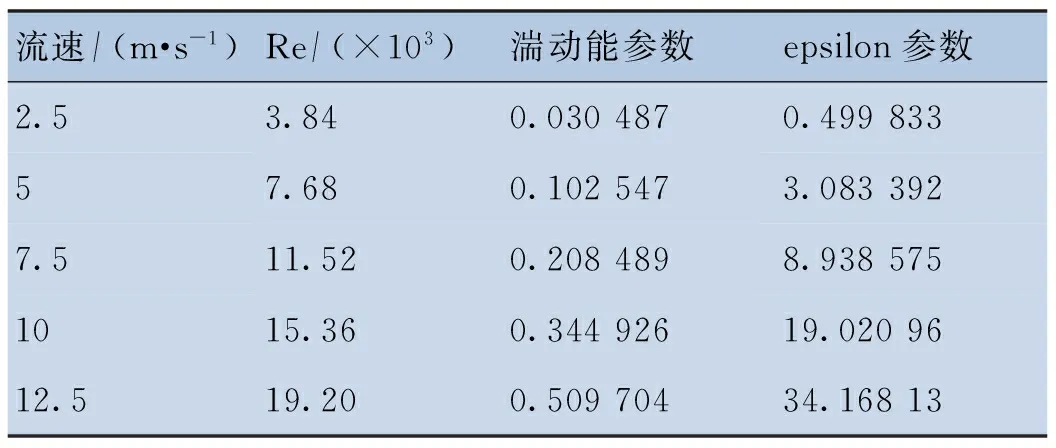
流速/(m·s-1)Re/(×103)湍动能参数epsilon参数2.53.840.0304870.49983357.680.1025473.0833927.511.520.2084898.9385751015.360.34492619.0209612.519.200.50970434.16813
流速为2.5 m/s时,流动处于临界区域,在进行数值模拟时,近似其流动为湍流,当流速增大时,流动处于湍流区。
2 光滑输气管道的数值模拟
2.1 光滑输气管道的阻力系数模拟值
对光滑输气管道的整个圆周及肋条相匹配的部分圆周进行数值模拟,h=s=0.51 mm V形肋条(一个肋)的圆心角约2.44°,h=s=0.90 mm V形肋条(一个肋)的圆心角约4.43°。表2为光滑输气管道的阻力系数误差值,误差值1对应于小尺寸的V形肋条误差百分比,误差值2对应于大尺寸的V形肋条误差百分比。
表2光滑输气管道的阻力系数误差值

流速/(m·s-1)整圆周模拟值h=s=0.51mm模拟值/(×10-4)h=s=0.9mm模拟值/(×0-4)误差值1/(%)误差值2/(%)2.50.0745.218.973.81.850.0574.006.972.61.77.50.0503.526.003.23.2100.0463.135.520.62.512.50.0432.925.110.73.2

2.2 V形肋条输气管道的减阻率
V形输气管道的减阻采用的是计算整个管道的总阻力系数,与光滑输气管道的模拟总阻力系数值进行对比,得到V形输气管的减阻率。表3为不同速度下V形肋条输气管的减阻率。
表3V形肋条输气管道减阻率

流速/(m·s-1)减阻率/(%)s=h=0.51mms=h=0.9mm2.53.31.253.52.97.55.7-2.3106.4-1.312.56.5-4.3

3 光滑输气管道与V形肋条管道的流场分析
取来流速度2.5 m/s,轴向1.5 m位置处的切平面,对小管径输气管道的流场进行分析,云图可以更直观地表现流场的差异。
3.1 速度云图分析
光滑输气管道与V形肋条管道速度云图见图2,如图2-a)所示,光滑输气管道的速度云图体现管道内流速的变化情况,在靠近壁面处,流速较小,而输气管道中心位置处的流速较大,满足圆管内的流速分布规律。而对不同尺寸对称V肋条输气管道的部分肋条输气管道进行分析,如图2-b)和2-c)所示,V形肋条输气管道在肋条位置的速度较小,靠近轴心位置的速度较大,h=s=0.51 mm的V形输气管道在靠近轴心位置的速度比h=s=0.90 mm的V形输气管道的小。这是由于沟槽底部的大部分流体受粘性作用影响,导致等价光滑表面以下的流体速度梯度变小,相当于增高粘性底层的厚度,壁面平均速度梯度较小,进而减小了边界层内流动剪切力,导致摩擦阻力减小,符合突出高度理论。
3.2 湍动能云图分析
对于小管径光滑输气管道,湍动能沿着径向分布是不均匀的,由壁面向轴心位置的径向距离不断增大,湍动能是先增大而后减小。不同流速下的湍动能也有同样规律,当流速较大时,湍动能也增大。小、大管径光滑输气管道与V形肋条管道湍动能云图见图3~4。在相同的天然气进口速度下,对于小管径V形输气管道,肋底湍动能较小,沿着径向方向指向轴心,湍动能先增大而后减小。而对于大管径光滑输气管道,湍动能沿着法向方向是变化的,随着法向距离的增大而逐渐增大;在展向方向是均匀分布的。对比不同尺寸的V形肋条,h=s=0.51 mm V形输气管道在靠近肋条顶部的湍动能要比h=s=0.9 mm V形输气管道的湍动能小,因此,h=s=0.51 mm V形输气管道具有减阻效果。这是由于肋条阻滞了流向涡,会在肋条顶部产生二次涡。沟槽的减阻效果主要是由于其尖角结构与湍流边界层内反向旋转的流向涡,使得沟槽底部能够保留较多的低速流体,多个沟槽作用下形成二次涡群,二次涡群将流向涡与沟槽底部分隔开,稳定沟槽底部的流场,达到减阻效果。
3.3 切应力云图分析
小、大管径光滑输气管道与V形肋条管道湍动能云图见图5~6。由图5~6可知,对于小管径输气管道,光滑输气管道切应力沿轴向方向分布不均匀,在入口处的切应力较大。切应力沿径向分布是均匀的。不同几何尺寸V形肋条输气管道切应力非均匀分布,在肋底切应力较小,在肋顶切应力较大。受入口处进口速度的影响,切应力较大。对于小管径管道,h=s=0.9 mm和h=s=0.51 mm的肋条,在肋顶处的切应力几乎相同。而对于大管径输气管道,光滑输气管道在展向位置的切应力是均匀分布的,由于入口段受来流影响,切应力较大,随着流向距离的增大,切应力逐渐减小。
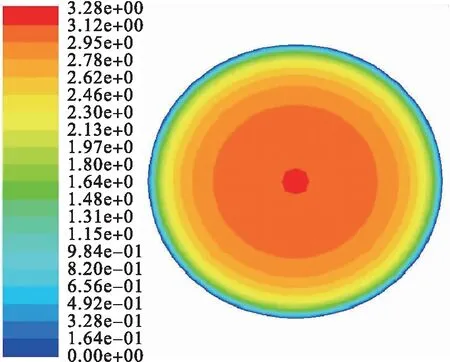
a)光滑输气管道
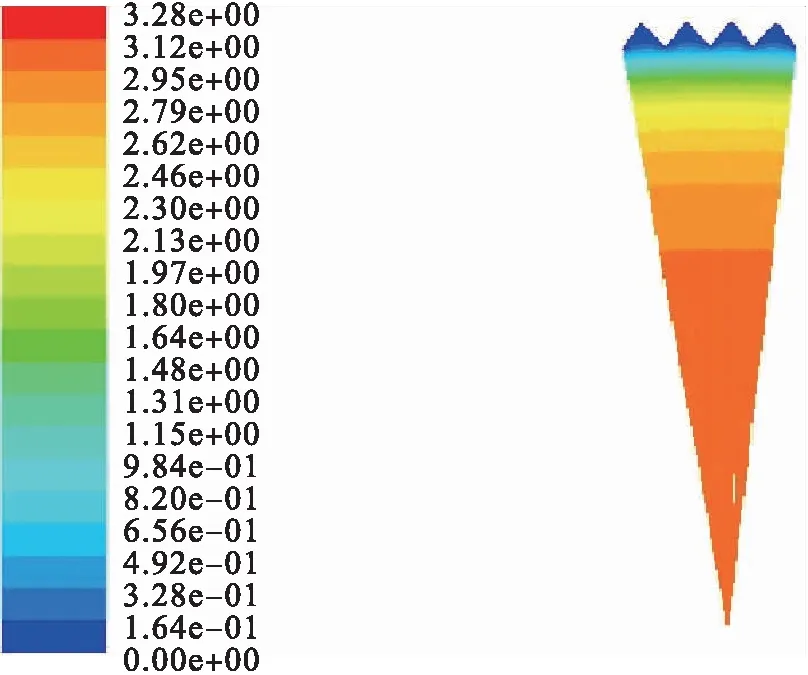
b)h=s=0.51 mm

c)h=s=0.9 mm
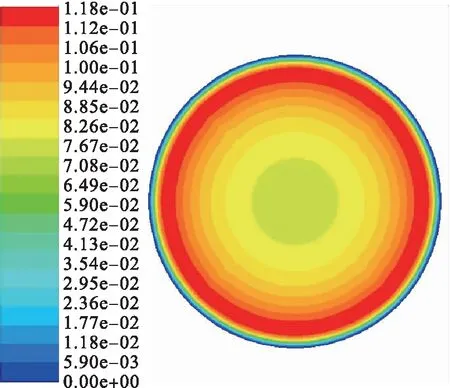
a)光滑输气管道
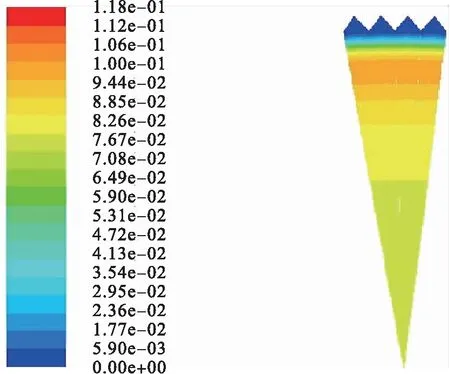
b)h=s=0.51 mm
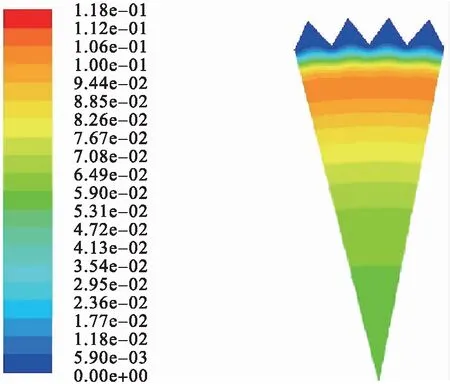
c)h=s=0.9 mm
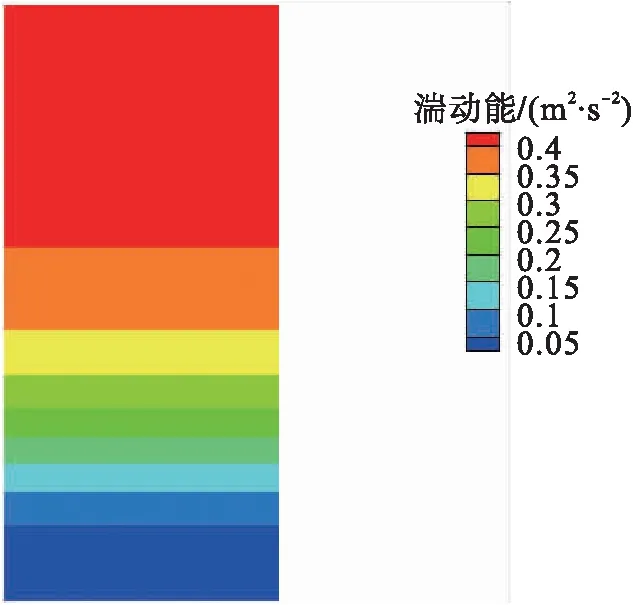
a)光滑输气管道

b)h=s=0.51 mm
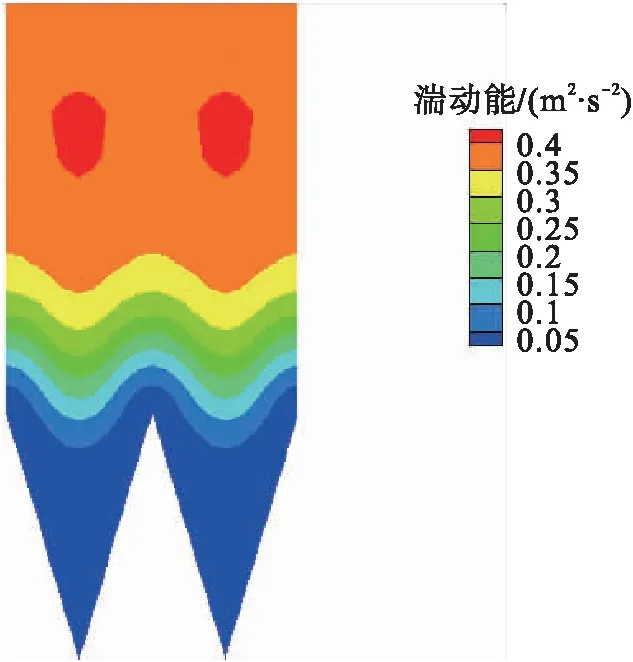
c)h=s=0.9 mm

a)光滑输气管道
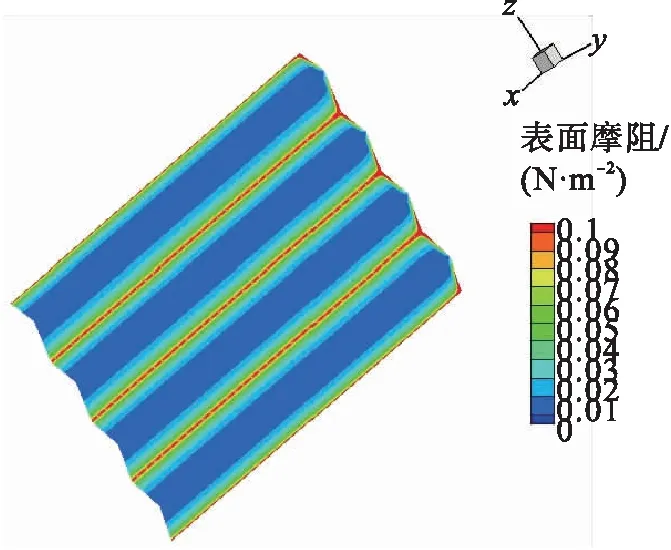
b)h=s=0.51 mm

c)h=s=0.9 mm
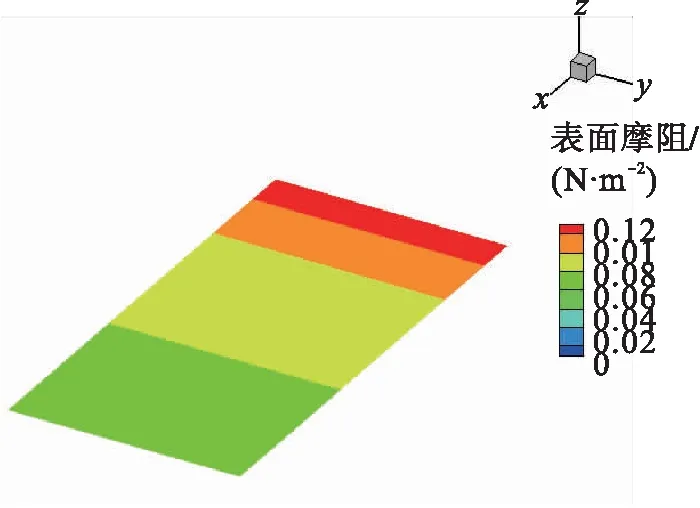
a)光滑输气管道

b)h=s=0.51 mm
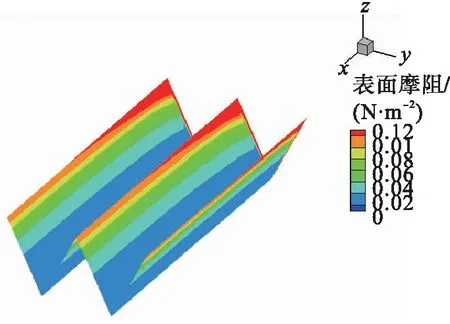
c)h=s=0.9 mm
4 结论

2)对于小管径输气管道,对称V形肋条输气管道在肋底速度较小,沿着径向方向指向轴心处的速度逐渐增大。靠近管壁位置的湍动能,h=s=0.51 mm对称V形肋条输气管道要比h=s=0.9 mm对称V形肋条输气管道小。而对于大管径输气管道,h=s=0.9 mm对称V形肋条输气管道比h=s=0.51 mm V形肋条输气管减阻效果好。
参考文献:
[1] 王剑波,王晓霖,陈建磊,等.天然气减阻剂研究进展[J].表面技术,2016,45(2):40-49.
Wang Jianbo, Wang Xiaolin, Chen Jianlei, et al. Research Progress in Drag Reducing Agents with Inhibition Performance for Natural Gas [J]. Surface Technology,2016,45(2):40-49.
[2] 张兴水,曹 杰.输气管道减阻内涂层与减阻剂应用现状及效益分析[J].油气储运,2013,32(6):675-678.
Zhang Xingshui, Cao Jie. Application and Economic Benefits of Internal Drag-Reduction Coating and DRA in Gas Pipeline [J]. Oil & Gas Storage and Transportation, 2013, 32(6): 675-678.
[3] 周 昊,徐 啸,赵会军,等.仿生非光滑表面减阻技术在油气管道中的应用[J].管道技术与设备,2014,(2):8-10.
Zhou Hao, Xu Xiao, Zhao Huijun, et al. Application of Biomimetics No-Smooth Surface Drag Reduction Technique to Oil and Gas Pipeline [J]. Pipeline Technique and Equipment, 2014, (2): 8-10.
[4] Choi H, Moin P, Kim J, et al. Direct Numerical Simulation of Turbulent Flow over Riblets [J]. Journal of Fluid Mechanics, 1993, 255(1): 503-539.
[5] Lee S J, Jang Y G. Control of Flow Around a NACA 0012 Airfoil with a Micro-Riblet Film [J]. Journal of Fluids & Structures, 2005, 20 (5): 659-672.
[6] 马付良,曾志翔,高义民,等.仿生表面减阻的研究现状与进展[J].中国表面工程,2016,29(1):7-15.
Ma Fuliang, Zeng Zhixiang, Gao Yimin, et al. Research Status and Progress of Bionic Surface Drag Reduction [J]. China Surface Engineering, 2016, 29 (1): 7-15.
[7] Hough G R. Drag Characteristics of V-Groove and Transverse Curvature Riblets [J]. Viscous Flow Drag Reduction, 1980, 72: 168-184.
[8] Bechert D W, Bruse M, Hage W, et al. Experiments on Drag-Reducing Surfaces and Their Optimization with an Adjustable Geometry [J]. Journal of Fluid Mechanics, 2000, 338: 59-87.
[9] 陈 莹,陈迎春,黄 炜,等.旋成体表面沟槽减阻试验研究[J].实验流体力学,2012,26(2):42-45.
Chen Ying, Chen Yingchun, Huang Wei, et al. Experiment Investigation of Drag Reduction Using Riblets for a Slender Body [J]. Journal of Experiments in Fluid Mechanics, 2012, 26 (2): 42-45.
[10] 谢 峰,王秀英,雷小宝.鲨鱼皮减阻结构的几何建模与数值分析[J].系统仿真学报,2014,26(7):1472-1476.
Xie Feng, Wang Xiuying, Lei Xiaobao. Geometric Modeling and Numerical Analysis on Drag Reduction Structure of Shark’s Surface [J]. Journal of System Simulation, 2014, 26 (7): 1472-1476.
[11] 李天然.仿生减阻表面的数值研究[D].大连:大连理工大学,2012.
Li Tianran. Numerical Study of Bionic Surface for Drag Reduction [D]. Dalian: Dalian University of Technology, 2012.
[12] Pauly C P. What is a Shark Doing in This Pump?[J]. World Pumps, 2001, 2001 (423): 15-16.
[13] Djenidi L, Antonia R A. Laser Doppler Anemometer Measu-rements of Turbulent Boundary Layer over a Riblet Surface [J]. AIAA Journal, 2012, 34 (5): 1007-1012.
[14] Neumann D, Dinkelacker A. Drag Measurements on V-Grooved Surfaces on a Body of Revolution in Axial Flow [J]. Applied Scientific Research, 1991, 48 (1): 105-114.
[15] 攸连庆.V形沟槽表面结构特征与减阻性能的关联性研究[D].大连:大连理工大学,2016.
You Lianqing. Study on the Relationship Between Structure Characteristics and Drag Reduction Performance of V Shaped Groove Surface [D]. Dalian: Dalian University of Technology, 2016.
[16] Walsh M J. Riblets as a Viscous Drag Reduction Technique [J]. AIAA Journal, 1983, 21 (4): 485-486.
[17] Walsh M J. Turbulent Boundary Layer Drag Reduction Using Riblets; Riblets as a Viscous Drag Reduction Technique [C]//Proceedings of the AIAA 20th Aerospace Sciences Meeting, January 11-14 1982, Orlando, Florida, USA. Reston: AIAA.
[18] Park S R, Wallace J M. Flow Alteration and Drag Reduction by Riblets in a Turbulent Boundary Layer [J]. AIAA Journal, 1994, 32(1): 31-38.
[19] 宋娟娟,徐 宇,黄宸武,等.非光滑表面湍流减阻的数值模拟研究[J].工程热物理学报,2011,32(5):771-774.
Song Juanjuan, Xu Yu, Huang Chenwu, et al. Numerical Simulation of Drag Reduction by Non-Smooth Surfaces in Turbulent Flow [J]. Journal of Engineering Thermophysics, 2011, 32 (5): 771-774.
[20] 黎润恒,赵成璧,唐友宏,等.三角形沟槽面圆管湍流减阻的大涡模拟数值研究[J].科学技术与工程,2013,13(8):2021-2026.
Li Runheng, Zhao Chengbi, Tang Youhong, et al. Large Eddy Simulation on Turbulent Drag Reduction over Triangle Riblet Surfaces of Pipes [J]. Science Technology & Engineering, 2013, 13 (8): 2021-2026.
[21] 于 洋,刘德俊.仿生肋条减阻技术在输气管道中的应用[J].辽宁石油化工大学学报,2017,37(4):23-28.
Yu Yang, Liu Dejun. The Application of Bionic Riblets on Drag Reduction in Gas Transmission Pipeline [J]. Journal of Liaoning Shihua University, 2017, 37 (4): 23-28.
[22] 刘德俊,于 洋,王国付,等.三种形状肋条减阻特性与机理研究[J].工程热物理学报,2016,37(7):1411-1415.
Liu Dejun, Yu Yang, Wang Guofu, et al. The Characteristic and Mechanism of Three Different Shapes of Riblets on Drag Reduction [J]. Journal of Engineering Thermophysics, 2016, 37 (7): 1411-1415.

