基于事件触发的航天器变周期控制方法研究*

孙 帅，王 磊,王志文

0 引 言

未来航天技术发展对控制系统自主性工作的要求日益提高，自主任务规划、自主控制、自主导航都是当前的研究热点领域[1].而自主性的技术实现建立在更大规模的星上数据传输与数据处理能力之上.此时，嵌入式系统信息资源如计算机处理能力、通信总线带宽等限制条件就成为了控制系统设计过程中不得不考虑的一些关键问题.本文针对星上嵌入式系统的通信带宽限制，设计了一种基于事件触发控制(event-triggered control，ETC)的新型航天器姿态控制方法，在保证控制性能的前提下大幅降低对星上通信带宽的负载.

航天器控制系统从动力学角度来看是一个典型的非线性系统，而从嵌入式角度出发，则是一个复杂的实时运动控制系统.只有统筹考虑两种设计视角，才能对系统进行进一步优化，达到既满足控制性能要求，又降低实时系统(计算、通信)负载的设计目的.文献[2-3]提出了信息物理系统(cyber-physical system, CPS)框架下的控制系统设计方法.就是将物理世界大量存在的同时具有通信、计算和控制过程且进行统一的建模与分析，最后达到提高系统性能，降低能耗与成本的目的.文献[4]给出了控制系统时序分析的基本模型，给研究有信息资源约束的控制系统设计问题奠定了基础.文献[5]从实时系统资源限制对控制系统性能影响的角度，阐述了实时系统与控制系统之间的关系.并给出了通过反馈调度(feedback scheduling)提高系统资源利用率以及通过任意时间控制(anytime control)降低控制算法计算负载的方法，来解决资源限制的问题.

而从另一个角度，由于目前嵌入式控制系统大多采用基于计算机控制理论的周期时间触发控制(periodic time-triggered control，PTTC)模式，所以研究者们就很自然的想到了可以通过延长控制周期，来降低控制频率，减轻实时系统运行代价[6-8].控制系统中状态量往往存在长时间的稳态过程，也就是平静周期(quiescent periods)，传统的时间触发等距采样方法在平静周期时也会保持恒定的采样速率，这就会对系统资源带来一定的浪费.因此，基于系统状态、输出以及其他可用信息来进行控制决策的，一种非周期控制模式——事件触发控制(event-triggered control，ETC)又一次回到了研究人员的视野.文献[9]是ETC的原始性文献，提出了在输入状态稳定(input-state stabilization，ISS)框架下建立了ETC的相关理论.文献[10-11]进一步拓展了ETC方法，延长了控制周期，提高了系统的鲁棒性.文献[12-14]将ETC技术应用在四旋翼无人机与望远镜的控制问题中，在保证控制的稳态性能、跟踪性能、抗干扰能力的前提下，降低了控制计算机与执行机构的通信频率，降低了实时系统的运行负载.文献[15]将ETC建立在扰动系统框架下，证明了满足指数稳定的系统，在特定的触发函数下能够实现稳定事件触发控制，并不存在Zeno现象[9].本文从信息物理融合的角度出发，提出了一种基于事件触发控制理论的航天器控制方法，与已有方法相比在保证控制性能前提下大幅降低了控制系统对通信网络的负载，使系统整体性能得到优化.

1 问题描述

航天器控制系统结构如图1所示，可以主要分为物理系统与信息系统两个部分.信息系统通过采样感知物理系统的状态变化并通过驱动执行机构来影响物理系统.对于信息系统来说，其工作流程可以由时序过程表示出来[4,16]，如图2所示.其中Ti为控制周期，在PTTC中一般认为控制周期是一个预先设定的常值；τi,1为采样延迟，为敏感器采集物理量并通过总线传输至嵌入式计算机的网络传输时间；τi,2为星载计算机计算时延，其长短主要取决于算法复杂度及处理器任务调度方式；τi,3为控制量到执行机构的通信时延，为控制指令发送至执行器的网络传输时间.

而对于小型航天器上通信总线而言，不光要传递控制系统间的数据交换，还要传递数管、热控等多个分系统的指令.而在通信过程中，一旦由于数据冲突发生丢包或时间抖动，都将对航天器整体性能造成不同程度的影响.所以在保证控制系统性能的前提下，减少其对实时通信的负载就显得尤为重要.

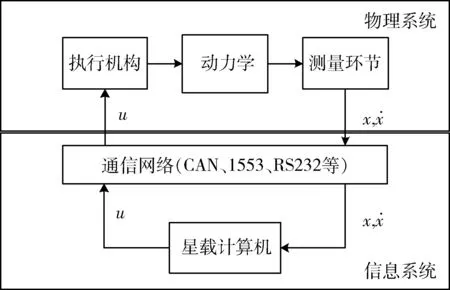
图1 航天器控制系统结构Fig.1 The structure of spacecraft control system

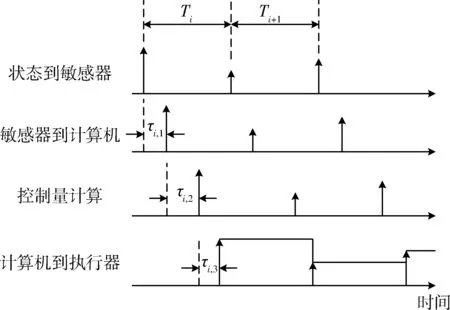
图2 航天器控制时序Fig.2 The timing of spacecraft control

定义1.对于一个通信总线而言，一个时间段内其负载可定义为

(1)

其中,n为总线上通信事件的个数，τi为通信传输时间，hi为任务的发送周期，而对于实时控制系统来说，hi一般可认为是控制任务的采样周期.

注1.其中τ取决于数据包的大小与总线速率，计算表达式为τi=8ai/υ，其中ai为数据包大小，单位为bytes，υ为总线传输速率，单位为bit/s.

定义2.为了对比研究，本文中定义在传统周期触发控制中，控制周期为100 ms时的总线负载为标称值U0.其他控制方法中总线负载标称值之比为相对负载，为ρ=U/U0.从定义可以看出ρ>0，且ρ越小就表明总线的负载越低.

一般的采样反馈控制系统可以描述为以下形式:

(2)

其中：x∈Rn;u∈Rm;f∶Rn×Rm→Rn，并在紧集上是Lipschitz连续，有f(0,0)=0;反馈控制律为K∶Rn→Rm，在紧集上Lipschitz连续;tk为采样时刻，k∈Z+.

而对于ETC系统，则可以描述为

(3)

其中h(x(tk),x(t))为事件方程.ETC问题的核心就在于事件方程的设计.

由式(3)可知，第k+1个控制输出更新时刻(以下简称为更新时刻)tk+1是由第k个更新时刻的状态量x(tk)与实时状态x(t)所决定的.也就是说如能增大更新周期ΔT=tk+1-tk，则可以减少控制输出的更新次数及所需的总线通信带宽，一方面能减轻实时系统负载，另一方面能节约系统能耗.

2 事件触发控制算法

为了方便研究，系统(2)可写为

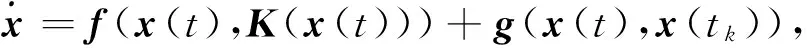
(4)

其中扰动项为

g(x(t),x(tk))=f(x(t),K(x(tk)))-f(x(t),K(x(t)))

(5)

则相应的标称系统即

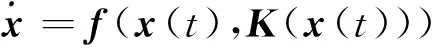
(6)

假设1.对于标称系统(6)，存在一个连续李亚普诺夫函数V∶Rn→R，并满足

(7)

(8)

(9)

引理1[17]. 令x(0)=0是标称系统(6)的一个平衡点，且存在一个李亚普诺夫函数V∶Rn→R使得(6)满足假设1, 同时扰动项(5)满足

(10)

其中θ,r∈(0,1).则原系统(4)为指数稳定，x(0)=0为其指数稳定平衡点.

引理2[15]. 考虑闭环ETC系统如下：

(11)

且当f,K在紧集上是Lipschitz的并且满足假设1,同时对于任意θ∈(0,1)，r>0，且满足

注2.从引理1-2可知，如果能找到一个反馈控制K∶Rn→Rm，使得系统能够指数稳定，则ETC系统(11)能够指数收敛于平衡点.

对于一般的刚体航天器姿态动力学与运动学特性，可用欧拉公式及四元数关系描述为[18]

(12)

(13)

(14)

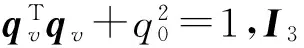
定理1.对于系统(12)～(14)，存在控制律

(15)

使得系统指数收敛于原点，其中kp,kd>0.

证明.对于系统(12)～(15)，设计Lyapunov函数

(16)

有唯一平衡点

[ωqvq0-1]T=0

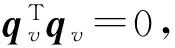
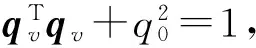
xTP2x≤V≤xTP1x

(17)

其中

(18)

对式(16)求导可得

(19)

代入控制律(15)，可得

(20)

其中有

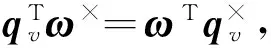
可得

(21)

(22)

根据上述推导，先只需选择合适的参数c，保证P1,P2,P3正定，即可证明(12)～(15)满足假设1.

由式(18)可知，如果P2>0，则一定有P1>0.应用Shur引理，P2>0等价于

(23)

定义γ为J最大特征值，则当满足

(24)

P1,P2>0成立.

对于P3，类似于以上步骤，可得当满足

(25)

综上所述，可以得到

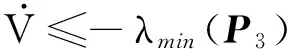
(26)

其中λmin(·),λmax(·)分别为矩阵的最小、最大特征值.再根据引理3.1可以得到

(27)

因此，姿态动力学系统(12)～(15)指数收敛于原点.

以误差变化量e为例，基本论域[-e，e] 中e表征误差大小的精确量，n是0～e范围内连续变化的误差离散化后分成的档数。它是构成基本论域的元素，一般情况下，档数分的越精细控制效果就会越好，但是档数越高，计算量就越繁琐，通常取n=6或7。

注3.kp,kd可以认为是PD控制中比例与微分的增益.一般来说高增益会带来更好的控制性能，但同时需要考虑到执行机构饱和及系统稳定裕度.

定理2.对于航天器姿态动力学系统(12)～(14)，当存在控制律与触发函数满足

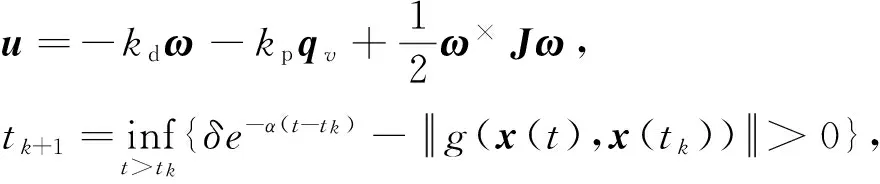
(28)

根据引理1、2和定理1易得.ETC系统(12)～(15)，(28)为指数稳定.

3 仿真实例

仿真对象为一个主惯量阵为[18]

的航天器.执行机构为在主惯量轴正向正交安装的3个偏置动量轮，每个动量轮的最大输出力矩是0.5 N·m，取控制器参数kp=7.9，kd=63.2；触发函数(28)中,δ=1.6，α=0.05；星上通信使用的RS422总线参数如下表1所示.

表1 通信总线参数Tab.1 The parameters of the bus

从图3可以看出，系统状态量均很快收敛，具有较好的稳态性能.其末端精度为8×10-3(°)，角速度精度为0.5×10-3(°)/s.

从图4上可以看出，因为控制输入的更新周期较大，所以控制力矩输出呈现明显的阶梯状.从图4下可以看出，触发函数一直保持在指数边界之下，说明ETC控制具有较好的收敛性.

从图5控制更新时间间隔来看，最长的控制更新间隔时间达到了9 s，这比在PTTC情况下0.64 s的更新间隔有了极大的延长，由此能够大幅降低通信频率.从表2可知，ETC相比于PTTC控制算法能够较大程度降低通信总线负载.ETC方法的总线负载仅为标称值的10.5%.

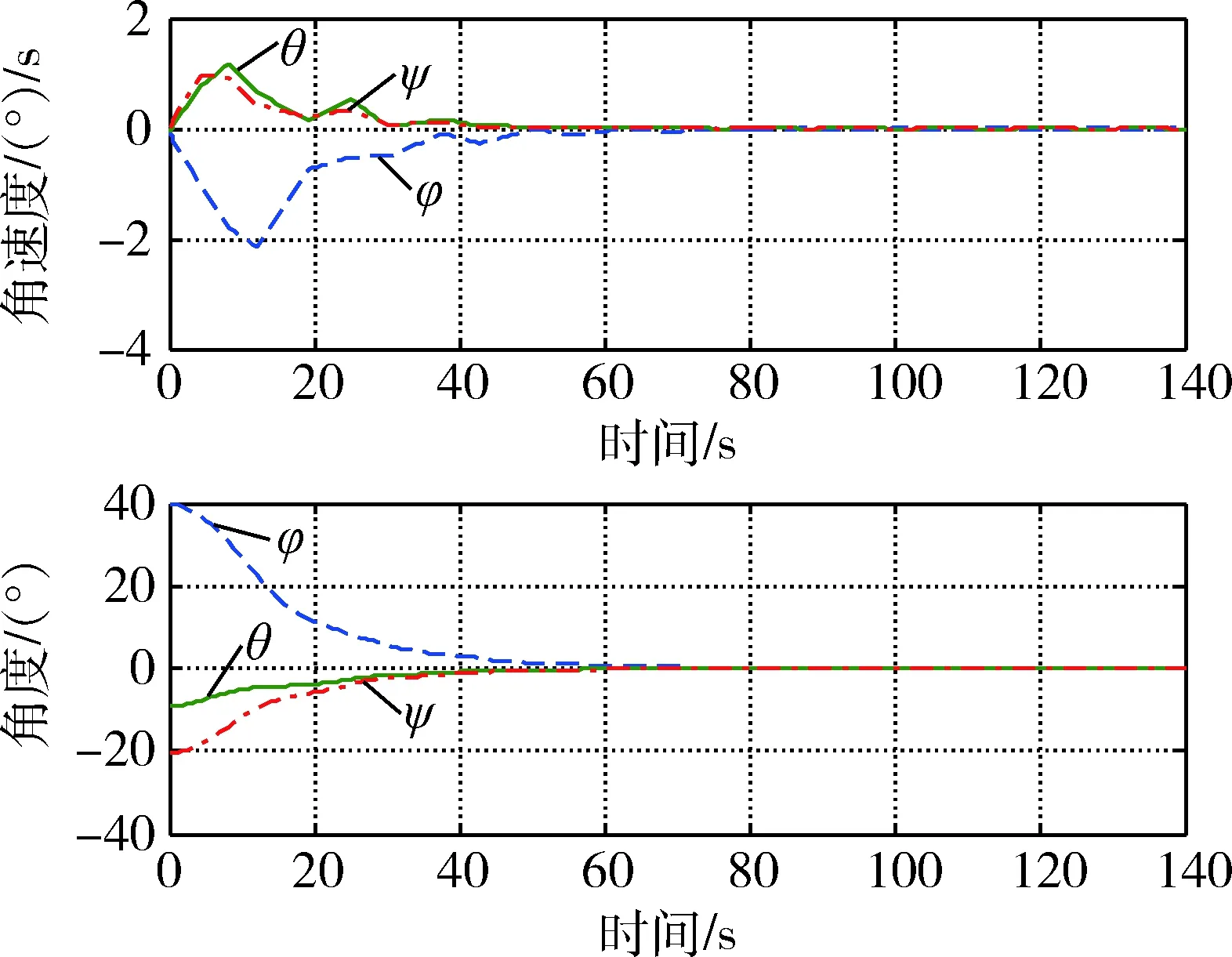
图3 ETC控制中系统状态变化Fig.3 The states variation under ETC

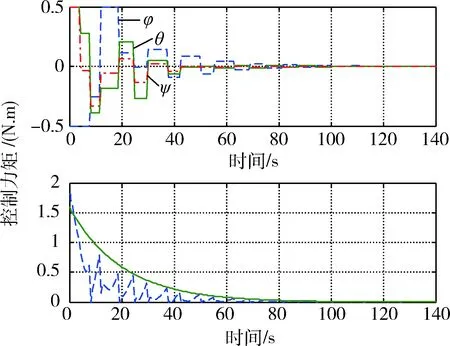
图4 控制输出与触发函数变化Fig.4 The output tongues and trigger function

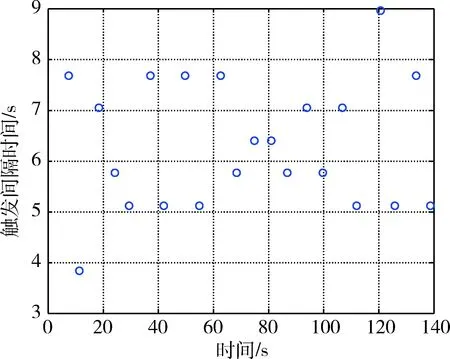
图5 ETC触发间隔时间Fig.5 The trigger interval of ETC

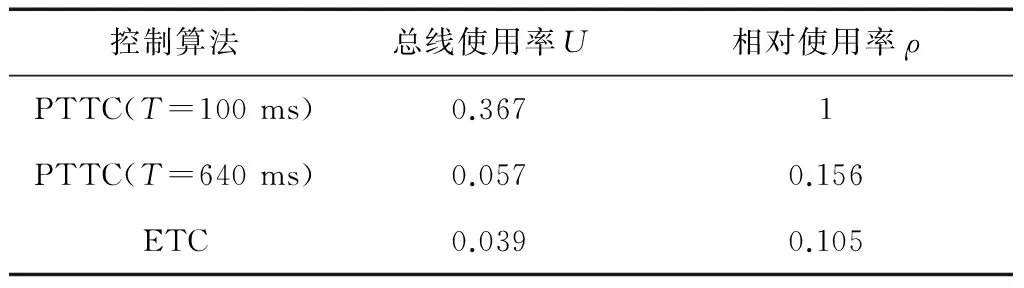
控制算法总线使用率U相对使用率ρPTTC(T=100ms)0.3671PTTC(T=640ms)0.0570.156ETC0.0390.105

4 结 论

本文主要研究了一类能有效降低航天器通信总线负载的基于事件触发控制的航天器姿态控制算法.该算法在保证控制性能的前提下能够大幅降低星上通信总线的带宽负载，能有效提高星上总线的共用能力，从根本上减少由于数据冲突造成的丢包、抖动等现象，从而提高航天器的整体性能.文中给出了此种方法的基本结构、设计流程及稳定性证明.最后通过仿真验证说明了算法的有效性.

参 考 文 献

[1] 吴宏鑫, 谈树萍. 航天器控制的现状与未来[J].空间控制技术与应用, 2012,38(5):1-7.

WU H X, TAN S P.Spacecraft control：present and future[J].Aerospace Control and Application, 2002, 38(5):1-7.

[2] LEE E A.Cyber physical systems: design challenges[C]//Proceedings of 11thIEEE international symposium on object oriented real-time distributed computing (ISORC). IEEE Computer Society, 2008: 363-369.

[3] 杨孟飞, 王磊, 顾斌,等. CPS在航天器控制系统中的应用分析[J].空间控制技术与应用. 2012,35(15):8-13.

YANG M F, WANG L, GU B,et al. The application of CPS to spacecraft control systems[J].Aerospace Control and Application, 2012,35(15):8-13.

[4] 王磊, 袁利, 戴居峰.卫星控制系统时序建模分析方法研究[J].空间控制技术与应用. 2014,40(3):31-35.

WANG L, YUAN L, DAI J F. Timing modeling and analysis method for satellite control system[J].Aerospace Control and Application. 2014, 40(3):31-35.

[5] ÅRZÉN K E, CERVIN A, EKER J. An introduction to control and scheduling co-design[C]//Proceedings of the 39thIEEE Conference on Decision and Control.New York:IEEE,2000.

[6] KUO B C.Digital control systems[M].Oxford University Press, 1992.

[7] POWELL J D,KATZ P. Sample rate selection for aircraft digital control[J].AIAA Journal, 1975,13(8):975-979.

[8] GLASSON D P. A new technique for multi-rate digital control design and sample rate selection[J].Journal of Guidance, Control, and Dynamics, 1982,5(4):379-382.

[9] PAULO T. Event-triggered real-time scheduling of stabilizing control tasks[J].IEEE Transactions on Automatic Control, 2007,52(9).

[10] MAHMOUD A, ROMAIN P, JAMAL D,et al. Input-to-state stabilization of nonlinear systems using event-triggered output feedback controllers[C]//European Control Conference (ECC). Linz,2015.

[11] WANG X F.Michael Lemmon. On event design in event-triggered feedback systems[J].Automatica, 2011, 47:2319-2322.

[12] GUERRERO-CASTELLANOS J F,TELLEZ-GUZMAN J J, DURAND S, et al. Attitude stabilization of a quadrotor by means of event-triggered nonlinear control[J].Journal of Intelligent & Robotic Systems, 2014, 73:123-135.

[13] SYLVAIN D, JONATHAN D,NICOLAS M,et al.Event based control for embedded and networked system: Application to a mini quadrotor helicopter using motion capture[C]//IEEE International Conference on Unmanned Aircraft System(ISUAS 2014). Orlando: 2014.

[14] BRUNO B, SYLVAIN D, JOHN J M M,et al. Attitude control of a gyroscope actuator using event-based discrete-time approach[C]//International Conference on Event-Based Control, Communication, and Signal Processing (EBCCSP). Krakow:2015.

[15] GAO Y F,WANG R, CHANG Y W, et al. Digital event-based control for nonlinear systems without the limit of ISS[J].IEEE Transactions on Circuits and Systems II: Express Brifs, 2017, 64(7):807-811.

[16] WITTENMARK B, NILSSON J, TORNGREN M.Timing problem in real-time control systems[C]//American Control Conference, IEEE. NEW YORK: 1995,2000-2004.

[17] KHALIL H.Nonlinear Systems 3rd edition[M].Upper saddle River, NJ: Prentice Hall, 2002.

[18] WU B. Spacecraft attitude control with input quantization [J].Journal of Guidance, Control, and Dynamics, 2015, 39, 1-5.