卫星导航系统失效性能分析与重构方法研究

赵 双，张雅声，戴桦宇，齐 跃

0 引 言

我国于2000年就开始建设具有自主知识产权的北斗卫星导航系统.目前，北斗卫星导航系统在轨运行的卫星数量已达31颗，预计在2020年左右完成全球组网，届时北斗将成为继美国的GPS和俄罗斯的GLONASS之后的又一个全球卫星导航系统[1].

卫星导航系统在星座的空间部署完成之后，星座的空间构型并不是一成不变的[2].当星座中的卫星因为系统故障或是空间碎片撞击而失效时，星座的空间构型和服务性能必然会受到影响.一般采用补发新的卫星来替换失效卫星，但由于受到新卫星研制周期、生产成本以及发射窗口的限制，该方法无法在短时间内快速恢复受损星座的服务性能[3]，若能够对星座中未失效卫星进行轨道机动来对星座重构，最大程度地修复和改善星座对目标区域或重点区域的服务性能，将尤其重要[4].星座重构按其过程大致可以分为重构构型设计和重构过程控制两个阶段，其中重构构型设计在整个星座重构任务中至关重要，是整个星座重构任务的基础和关键，决定了重构后的星座性能；重构过程控制是指将受损后的星座从初始构型变换到重构构型的机动方式和变轨手段，是构型重构的实现手段.

1 卫星导航系统失效性能分析

自1993年信号覆盖性、服务可用性、服务可靠性和定位精度4个导航星座性能指标被提出以来[5]，随着卫星导航技术的快速发展，卫星导航系统的应用范围越来越广，人们对导航星座的性能要求越来越高，描述导航星座性能的指标也越来越多，导航星座性能指标主要有：连续覆盖指标、空间构型指标、冗余维持指标、构型保持指标和自主性能指标[6].本文主要采用空间构型指标来对卫星导航系统的性能进行分析.

1.1 导航星座空间构型指标

空间构型指标[7]：用来描述某一时刻用于定位解算的4颗卫星与用户之间的相对位置，以及卫星与用户所构成的几何体强度，一般采用精度因子来度量.对于导航星座而言，最关心的就是其定位精度.其受到各伪距测量值的影响并取决于星座的空间构型[8].在导航领域中一般称为精度因子(dilution of precision，DOP).

如图1所示，某时刻地面接收机选择用于定位解算的4颗卫星分别为S1、S2、S3、S4，地心惯性坐标系下接收机的位置矢量为Ru(Xu,Yu,Zu)，卫星到接收机的位置矢量为Ri(Xi,Yi,Zi).(其中i=1、2、3、4)

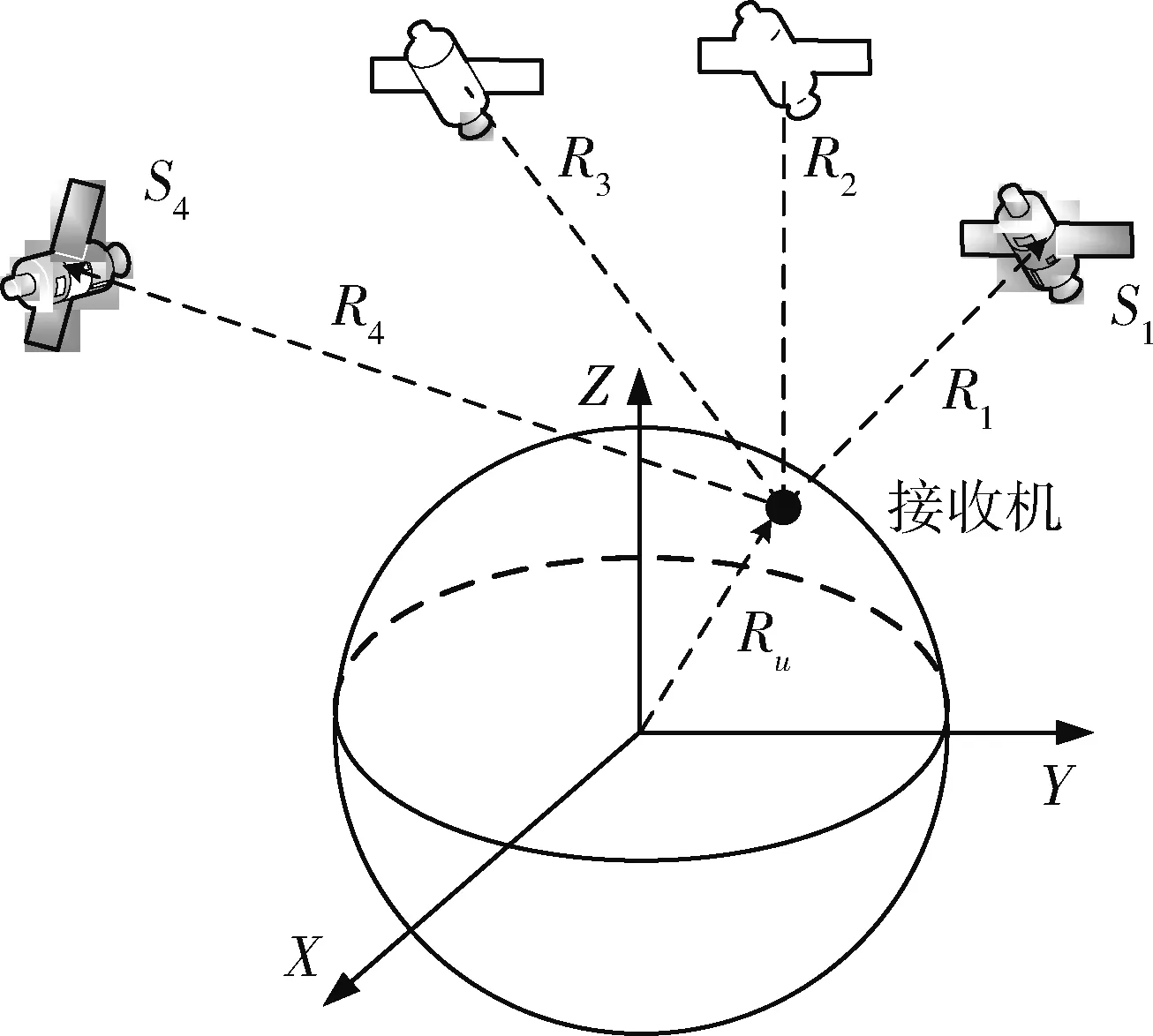
图1 卫星与接收机的位置关系Fig.1 Position relation between satellite and receive

卫星到接收机的位置矢量的模长为：

(1)

可得位置矩阵：

(2)

通过对位置矩阵进行变换得到DOP矩阵D：

D=[PTP]-1

(3)

将D分解为如下形式：

(4)

根据矩阵D中的各个元素，对各DOP值进行求解.包括：GDOP(几何精度因子)DG、PDOP(位置精度因子)DP、HDOP(水平精度因子)DH、VDOP(垂直精度因子)、TDOP(时间精度因子)DT.

(5)

其中GDOP值可以由PDOP值和TDOP得到：

(6)

GDOP即考虑了时间上的误差又考虑了空间上的误差，比其他精度因子更全面也更严苛，所以本文选用GDOP值作为衡量导航星座定位精度的指标.通常认为：DG<<6时，星座的定位精度良好，定位误差较小；610时，星座的定位精度较差，定位误差急剧增大[9].

选用网格点法[10]分析某一时段内导航星座对目标区域的定位精度时.通过对目标区域内的所有网格点每一时刻的GDOP值进行统计，得到仿真时段内目标区域GDOP值的统计量，并用该统计量来表示导航星座对目标区域的定位精度.

1.2 满站位状态下的北斗卫星导航系统星座性能分析

与GPS和GLONASS不一样，建成后的北斗卫星导航系统由3种轨道类型共35颗卫星组成，包括3颗IGSO卫星、5颗GEO卫星和27颗MEO卫星.其中，5颗GEO卫星的定点经度分别为东经58.75°、80°、110.5°、140°、160°；3颗IGSO卫星分布在3个轨道倾角为55°的同步轨道上，交叉点地理经度为东经118°，且3颗卫星的星下点轨迹相互重合，相位角相差120°；27颗MEO卫星均匀地分布在3个轨道倾角为55°的圆轨道面内，轨道高度为21 500 km.本文在研究卫星导航系统的星座性能和重构构型时，均以建成后的北斗全球卫星导航系统为研究对象，根据北斗卫星导航系统的空间布局和构型特征，设定1 Jan 2020 00:00:00.000 UTCG时北斗卫星导航系统的空间构型如图2所示，并对星座中的35颗卫星进行编号.

图2 北斗卫星导航系统星座构型Fig.2 Constellation configuration of Beidou satellite navigation system

设定目标区域为亚太区域(东经55°～东经180°，南纬55°～北纬55°)，仿真时段为[1 Jan 2020 00:00:00.000 UTCG]～[ 8 Jan 2020 00:00:00.000 UTCG]，地面网格分辨率为2°×2°，时间步长为600 s.利用仿真软件得到了该时段内目标区域的平均GDOP值随时间的变化，如图3所示.结果显示，整个仿真时段内，不同时刻目标区域的平均GDOP值的变化范围为1.246 6～1.263 4.

图3 目标区域的平均GDOP值随时间的变化Fig.3 The change of the mean GDOP value with time in the target area

仿真时段内目标区域的平均GDOP值分布如图4 所示.结果显示，整个仿真时段内，不同网格点的平均GDOP值的变化范围为1.110 8～1.446 1.

图4 目标区域的平均GDOP值分布Fig.4 The mean GDOP distribution of target region

对目标区域内所有网格点的仿真数据进行统计，可以得到整个仿真时段内目标区域的平均GDOP值为1.255 9.从图2中可以看出，仿真时段内不同时刻目标区域的平均GDOP值在1.255 9附近小幅度的波动，并呈现出一定的周期性.图3中由于星座中的卫星关于赤道面对称分布，使得目标区域内平均GDOP值的分布也关于赤道对称.

1.3 卫星失效位状态下的北斗卫星导航系统星座性能分析

根据失效卫星所处的轨道面和失效卫星的数量，将失效模式分为单颗卫星失效和多颗卫星失效，其中多颗卫星失效又分为共面多颗卫星失效和非共面多颗卫星失效.根据失效卫星的轨道类型，又可以将失效模式分为IGSO、GEO、MEO、IGSO+GEO、GEO+MEO和IGSO+MEO卫星失效.

(1)单颗和多颗卫星失效

针对单颗卫星失效和多颗卫星失效，本文主要分析1颗和2颗卫星失效时目标区域平均GDOP值的变化.如图5所示，可以发现单颗卫星失效情况下，亚太区域的平均GDOP值在1.263 8～1.285 9之间变化，且只有当编号为5的卫星(GEO卫星中定点经度为80°的卫星)失效时，平均GDOP值最大为1.285 9.

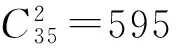
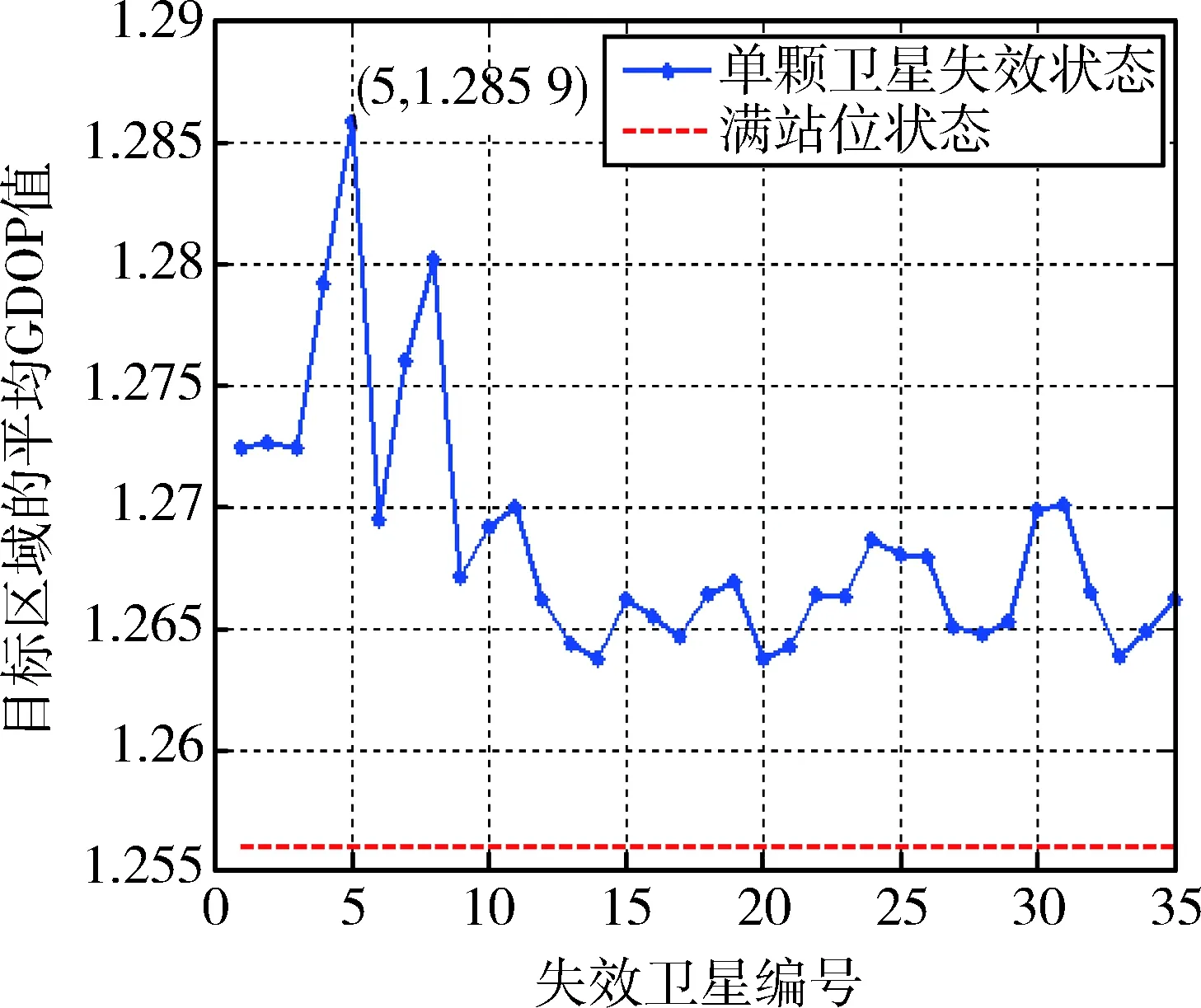
图5 单颗卫星失效下目标区域的平均GDOPFig.5 The average GDOP of the target region under the failure of a single satellite

如图6所示，可以发现两颗卫星失效情况下，亚太区域的平GDOP值在1.284 8～1.334 9之间变化.对于共面的两颗卫星失效而言，只有当失效卫星组合编号为100的时候，即卫星编号为4和5(GEO卫星中定点经度为58.75°和80°)的两颗卫星失效时，平均GDOP值最大为1.334 9；对于非共面的两颗卫星失效而言，只有当失效卫星组合编号为37，即卫星编号为2和5(IGSO卫星中升交点赤经为97.857°真近点角为120°的卫星和GEO卫星中定点经度为80°)的两颗卫星失效时，平均GDOP值最大为1.317 5.

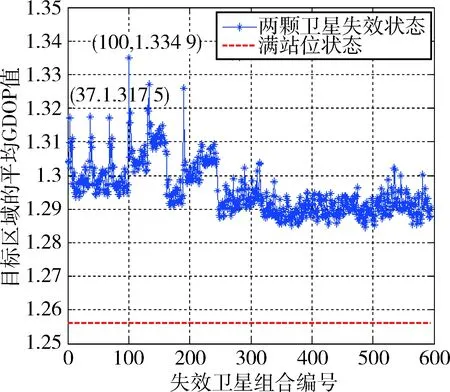
图6 两颗卫星失效下目标区域的平均GDOP值Fig.6 The mean GDOP value of the target region under the failure of the two satellites

(2)不同轨道类型卫星失效

针对不同轨道类型的卫星失效，在同样的仿真时段得到了IGSO、GEO、MEO、IGSO +GEO、GEO+MEO和IGSO+MEO六种轨道类型的卫星失效时目标区域的平均GDOP值，如表1所示.相比于满站位状态下目标区域的平均GDOP值而言，当IGSO、GEO、IGSO+GEO卫星失效时，该指标均有一定程度的劣化，但星座性能变化不大；当MEO卫星失效时星座仍能对目标区域提供正常的导航与定位服务；当GEO+MEO卫星失效时，星座中卫星数小于4，不再具备导航与定位能力；当IGSO+MEO卫星失效时，此时亚太区域的平均GDOP值远大于6，可以认为此时的星座也不具备导航与定位能力.

表1 不同轨道类型的卫星失效时目标区域的平均GDOP值Tab.1 The average GDOP values of target regions in different types of satellite failure

2 导航星座重构方法研究

2.1 基于遗传算法的重构构型设计

(1)目标函数与优化变量

与星座构型设计一样，重构构型设计也属于优化问题.但与星座构型设计最大的区别在于重构构型设计是以受损后的星座构型为基础，星座构型设计考虑的多是星座的研制成本、发射代价、运营成本等，而受损星座的重构构型设计考虑更多的则是重构后星座性能的提升程度等，本文以重构后的星座性能指标(目标区域的平均GDOP值)为重构构型设计的目标函数.

(2)优化变量

理论上而言，所有对重构构型产生影响的变量都可以作为优化变量，但为了保证重构后星座构型的稳定性，本文在对受损星座中在轨卫星的轨道参数进行调整时，仅改变卫星的相位角即卫星在轨道上的位置而保持其他参数不变[11].即优化变量为：Satamo所需调整的卫星数；Satadj被调整卫星的编号所组成的集合；fi(i∈Satadj)编号为的卫星重构后的真近点角；

(3)优化方法

被调整的卫星数与所调整卫星的编号是离散变量，卫星的真近点角是连续变量，对于离散和连续变量共存的优化问题本文选择遗传算法进行求解.遗传算法(genetic algorithm，GA)是智能优化算法中的一种，自1975年提出以来，一直被誉为一种非常高效的全局优化器[12].GA算法的实现步骤主要包括解编码、个体适应度评估和遗传运算(选择、交叉和变异).

(4)染色体的编码方式

遗传算法中定义种群为编码后的染色体集合，表征每个个体的是其相应的染色体，针对重构构型设计而言，被调整的卫星数直接决定了染色体的长度，但被调整的卫星数作为一个变量也是不确定的，所以造成染色体的长度也不确定，不同长度的染色体之间无法直接进行变异和交叉等操作，为此本文采用了双层编码的方式[13]，如图7所示.

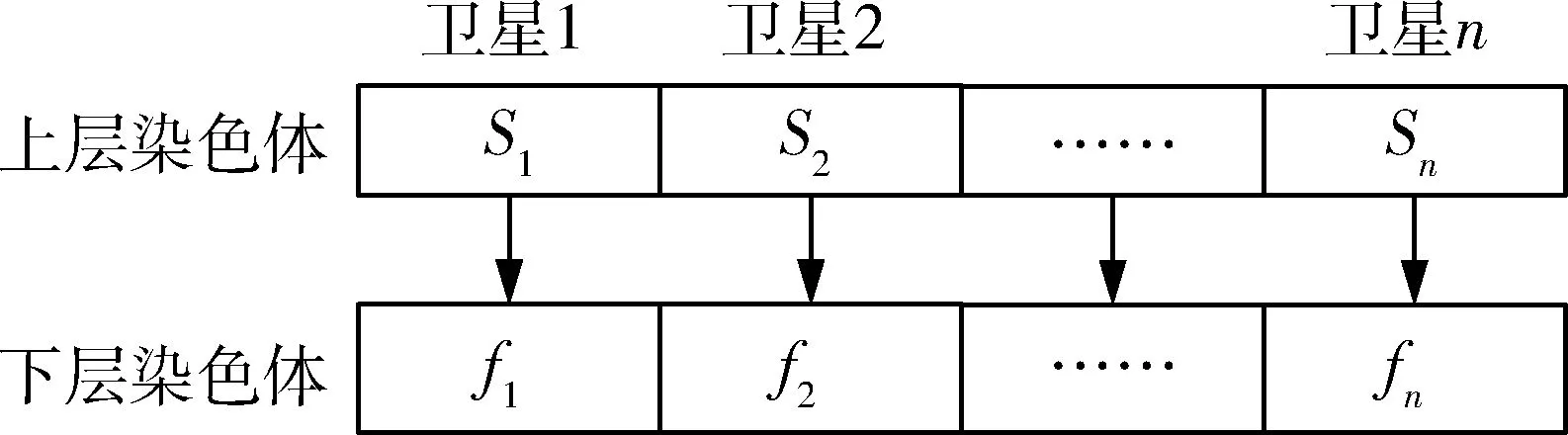
图7 双层编码示意图Fig.7 The sketch map of double coding

图中Si表示重构过程中每颗卫星的状态，Si=1、Si=0分别对应于编号为i的卫星在重构过程中被调整以及未被调整.上层染色体通过解码可以得到被调整的卫星数和被调整卫星的编号：

(7)

下层染色体代表了重构后每颗卫星的真近点角，但是并非下层染色体中的所有基因都能起作用，下层染色体的基因是隐性还是显性取决于该卫星的状态函数，如果上层染色体中某一颗卫星的状态函数等于1，则下层染色体中与之对应的为显性基因，反之则为隐性.采用双层编码方式后，不管参与重构的卫星数是多少，染色体的长度都是相同的，不同染色体代表的个体之间可以直接进行交叉、变异等操作产生新的个体.

(5)仿真算例

以MEO卫星失效为例，仿真时段仍为[1 Jan 2020 00:00:00.000 UTCG]～[ 8 Jan 2020 00:00:00.000 UTCG]，目标区域为亚太区域，设定初始种群的大小为30，进化代数为200，种群交配的概率为0.90，种群变异的概率为0.09，利用遗传算法得到每一代种群所对应的目标区域平均GDOP值随进化代数的变化图像，如图9所示.

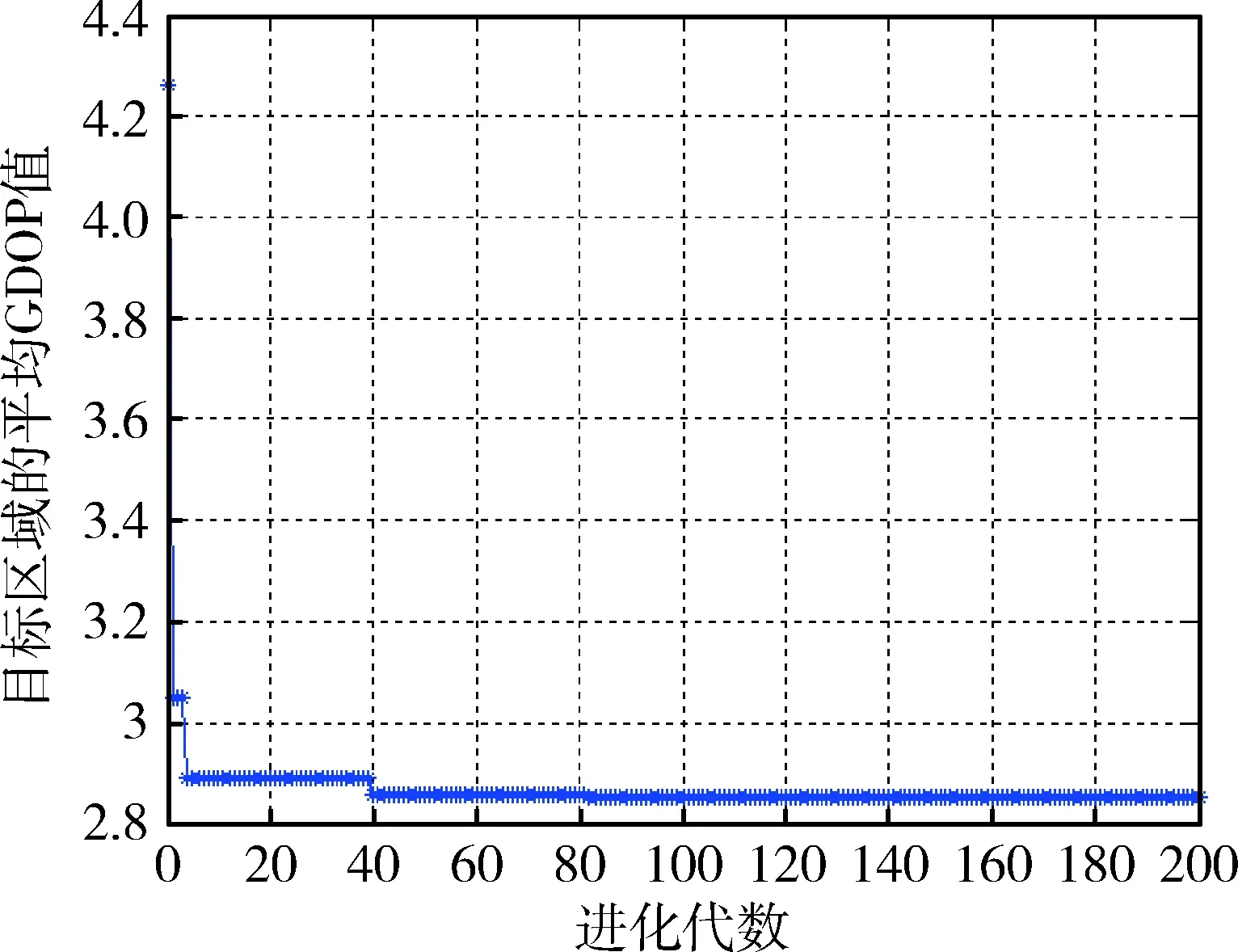
图8 遗传算法的优化过程Fig.8 The optimization process of genetic algorithm

从图8可以看出，通过对重构构型的优化将星座对目标区域的平均GDOP值从4.263 1降至2.855 5，并对遗传算法得到的最佳染色体进行解码得到MEO卫星失效下的重构方案如表2所示.

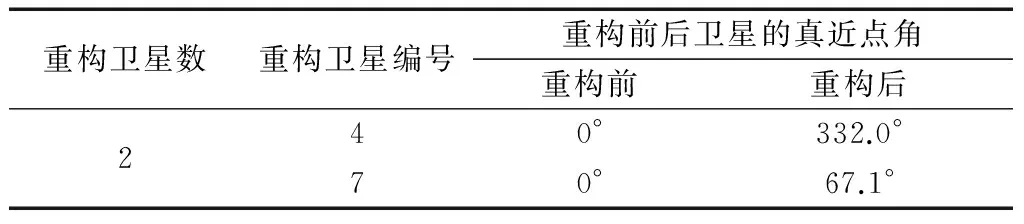
表2 MEO卫星失效时的星座重构方案Tab.2 The constellation reconstruction scheme for MEO satellite failure

2.2 重构过程控制

确定了仅对星座中未受损卫星进行相位机动的原则下，根据调相过程中是否涉及轨道面间的机动而将卫星相位调整方式分为：共面轨道相位机动和非共面轨道相位机动.考虑到非共面变轨和共面变轨在能量消耗上的差异，本章选择共面轨道相位机动的方式来改变星座中卫星的相位角.共面轨道相位机动又分为：共面低轨变相和共面高轨变相.

在共面轨道相位调整中，初始位置与目标位置之间的位置关系可以分为相位超前与相位滞后两种[14].从初始位置沿着卫星在轨道上的运行方向到目标位置所转过的角度为θ其中：

(8)

实际问题中，综合考虑机动时间和机动能量，一般对于相位超前采取共面高轨变相(如图9所示)，相位滞后采取共面低轨变相[15].

图中原始轨道为圆轨道其轨道半长轴为a0，转移轨道的轨道半长轴为a，初始位置和目标位置的真近点角为f0、f.第一次变轨时，卫星在原轨道上的速度为v1，卫星进入转移轨道后的速度为v2：

(9)

式中，μ为地球引力常数.

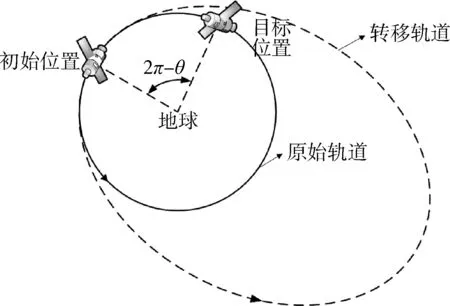
图9 相位超前的共面高轨变相示意图Fig.9 The schematic diagram of phase ahead of coplanar high orbit

第一次变轨和第二次变轨的速度增量分别为Δv1和Δv2，完成相位调整所需要的总能量为ΔV

(10)

这一过程中，位于初始位置的卫星在转移轨道上等待的圈数为Ntra，位于目标位置的卫星在原始轨道上运行的整圈数为Norg，完成相位调整所需要的总时间为ΔT

(11)

式中，θ的取值由初始位置和目标位置的真近点角而定，因为是高轨变相，所以转移轨道的半长轴必须满足：

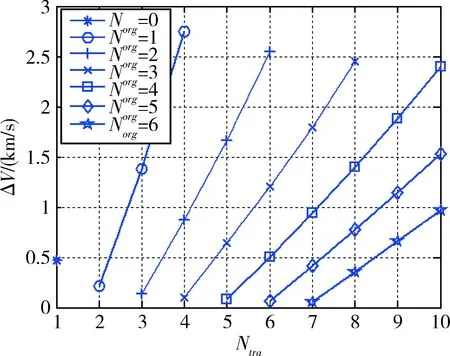
a0

(12)

假设在星座重构过程中具备同时调整两颗及以上卫星的能力，对于整个星座而言，完成重构所需要的总能量Trec和总时间Trec

(13)

式中，i∈Satadj，ΔVi和ΔTi分别为所调整卫星中编号为i的卫星完成重构所需要的总能量和总时间.

针对相位滞后的情况，利用低轨变相的方法来调整卫星在轨道上的相位角.与低轨变相的区别在于转移轨道的半长轴所满足的约束条件不同，对于低轨变相而言有：

(14)

式中，Re为地球半径.

根据重构构型的优化结果，将受损后的星座从初始构型变换至重构构型的过程中需要将编号为4和7的卫星，从轨道上真近点角为0°的位置机动至真近点角为332.0°和67.1°的位置，假设重构时间Trec≤7天，利用上述相位机动模型可以得到所有满足条件的机动方案，如图10～11所示.

图10 编号为4的卫星的所有相位机动方案Fig.10 All phase maneuver schemes for satellites numbered 4

图11 编号为7的卫星的所有相位机动方案Fig.11 All phase maneuver schemes for satellites numbered 7

从图10～11可以看出：对于编号为4的卫星，最佳相位机动方案为Norg=6,Ntra=6,ΔV4=0.026 km/s，此时转移轨道半长轴为42 529.86 km，机动耗时6.06D；对于编号为7的卫星，最佳相位机动方案为Norg=6,Ntra=7,ΔV7=0.056 km/s，此时转移轨道半长轴为41 414.37 km，机动耗时6.80天.对于星座而言重构时间Trec=max(ΔT4,ΔT7)=6.08天，重构能量Vrec=ΔV4+ΔV7=0.082 km/s.

3 结 论

(1)以GDOP值为性能指标，分别分析了单颗、两颗卫星失效以及不同轨道类型卫星失效下的星座性能.

(2)以提升目标区域的平均GDOP值为重构目的，以重构控制的卫星数、重构卫星的编号以及重构后卫星的真近点角为优化变量，建立重构构型优化模型并利用遗传算法进行求解.

(3)建立相位超前和相位滞后两种情况下的相位机动模型，依据得到的重构构型给出最佳的相位机动方案.

参 考 文 献

[1] 北斗发射一览表[EB/OL].http://www.beidou.gov.cn/xt/fsgl/Beidou satellite launch list[EB/OL].http://www.beidou.gov.cn/xt/fsgl/.

[2] 张育林, 范丽, 张艳. 卫星星座理论与设计[M].科学出版社, 2008.

ZHANG Y L，FAN L，ZHANG Y. Theory and design of satellite constellations[M].The Science Publishing Company,2008.

[3] 于小红, 冯书兴. 区域观察小卫星星座重构方法研究[J].宇航学报, 2003, 24(2):168-172.

YU X H，FENG S X. Study on reconfiguring method of small satellite constellations for regional observation[J].Journal of Astronautics,2003, 24(2):168-172.

[4] PARK C W. Coverage analysis in case of faults of some satellites in low earth orbit satellite constellations[J].Aerospace Conference,1998.

[5] 胡志刚. 北斗卫星导航系统性能评估理论与试验验证[D].武汉大学, 2013.

HU Z G. Performance evaluation theory and test verification of the Beidou satellite navigation system[D].Wuhan University, 2013.

[6] KOTHRIS D, BEACH M, ALLEN B, et al. Performance assessment of terrestrial and satellite based position location systems[C]//3G Mobile Communication Technologies. Second International Conference on IET, 2002:211-215.

[7] ZOGG J. Gps-essentials of satellite navigation compendium[R]. Technical report.u-blox AG, 2009.UBLOX.

[8] 陈岩,董淑福,陈晖,等.BD-2几何精度因子仿真分析[J].通信技术,2010, 43(3):112-114.

CHEN Y，DONG S F，CHEN H，et al. Simulation analysis of geometric dilution of precision[J].Communications Technology,2010, 43(3):112-114.

[9] 帅平,曲广吉.卫星导航定位方程的病态条件[J].飞行器测控学报,2006, 25(1):1-5.

SHUAI P，QU G J. Morbid conditions for the positioning equation of satellite navigation[J].Journal of Spacecraft TT&C Technology,2006, 25(1):1-5.

[10] 徐敏,程凤舟,陈士橹.星座覆盖性能数值仿真[J].宇航学报,2000, 21(s1):11-17.

XU M，CHENG F Z，CHEN S L. Numerical simulation of constellation coverage performance[J].Journal of Astronautics,2000, 21(s1):11-17.

[11] 胡伟,王劼.基于遗传算法的全球导航星座重构研究[J].宇航学报,2008, 29(6):1819-1823.

HU W，WANG J. Research on global navigation constellation reconstruction based on genetic algorithm[J].Journal of Astronautics, 2008, 29(6):1819-1823.

[12] 王瑞,马兴瑞,李明.采用遗传算法进行区域覆盖卫星星座优化设计[J].宇航学报, 2002, 23(3):24-28.

WANG R，MA X R，LI M. Optimization design of regional coverage satellite constellation using genetic algorithm[J].Journal of Astronautics, 2002, 23(3):24-28.

[13] 陈盈果.面向任务的快速响应空间卫星部署优化设计方法研究[D].国防科学技术大学,2014.

CHEN Y G. Research on task oriented optimization design method for fast response space satellite deployment [D].National University of Defense Science and technology，2014.

[14] 张雅声,张育林.性能修复型星座快速重构方法研究[J].装备学院学报, 2005, 16(4):66-72.

ZHANG Y S，ZHANG Y L. Study on the method of rapid reconstruction of the constellation of performance repair[J].Journal of Institute of Command and Technology, 2005, 16(4):66-72.

[15] 杨洋,董绪荣,范丽,等.混合导航星座卫星重构方法研究[J].上海航天,2012, 29(4):19-21.

YANG Y，DONG X R，FAN L，et al. Research on the method of satellite reconstruction of mixed navigation constellation[J].Aerospace Shanghai, 2012, 29(4):19-21.