面向海洋机动目标跟踪监视的卫星重构组网优化与仿真*

赵程亮，张占月，李志亮，刘 瑶

0 引 言

海洋机动目标主要指海洋移动舰船等军事或民事目标，对海洋机动目标进行跟踪监视，无论是在军事中反恐维稳、打击引导指示，还是在民事搜救、抢险救灾中，都具有实际应用意义[1-2].在对海洋机动目标的跟踪监视中，采用成像卫星对其进行搜索具有成像范围广、不受地域、空域限制等搜索优势[3]，但受卫星运行轨道周期限制的缘故，卫星过顶成像时间不能自由支配，并且相邻卫星过境观测时间具有较长的时间间隔，同时海洋机动目标还具有广阔的移动范围以及一定的机动能力，因此对其跟踪监视起来非常困难，目前针对机动目标搜索观测的研究主要通过在轨卫星任务规划完成，BERRY等[4]将海洋机动目标监视任务分为相互独立的三个阶段—搜索、定位和跟踪，并在空间监视任务共同求解框(Gauss-Markov and Bayesian inference technique,GAMBIT)的基础上对各个搜索阶段进行卫星调度规划，实现对海洋机动目标的跟踪监视.文献[5-7]基于机动目标先验信息和目标运动预测技术，通过对卫星观测条带与过境窗口的选择调度，得到最优的机动目标侦察方案.这些研究通过在轨卫星任务规划对海洋机动目标搜索监视取得了一定的研究成果，而在实际工程运用中，有可能出现在卫星最大侧摆角度内不能对感兴趣区域或先验信息下目标出现概率较大区域进行成像观测的情况，由于对机动目标的搜索观测具有较高的时效性要求，错失一次成像机会即可导致跟踪监视失败.此时，若卫星具有一定的轨道机动能力，在卫星过顶成像之前调整卫星的相位，从而使卫星过顶成像时星下点轨迹向西或向东偏移，结合任务规划可以对机动目标搜索监视实现较大收益.因此本文主要内容是建立一定先验信息下目标运动预测模型，在已有卫星无法满足机动目标跟踪监视需求的情况下，通过部分卫星相位调整实现对海洋机动目标的搜索跟踪监视.

1 目标运动预测模型

卫星相位调整组网观测需要建立在对目标先验信息比较高的情况下，目标潜在运动区域预测模型比较精准，可更好实现对机动目标的跟踪监视.当前对海洋机动目标的运动预测模型主要有航位推测法、曲线拟合法、典型路径法等多种运动模型，其中航位推测法对机动目标的先验信息要求比较高、同时对下一时刻目标潜在运动区域也比较精准，本文采用文献[5]中坐标系转移方法，建立地理坐标系下机动目标航位预测模型，具体步骤如下.

1.1 二维平面坐标系下目标运动预测模型

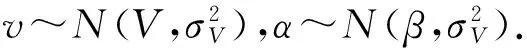
(1)

(2)

转换为直角坐标方程为：

(3)

式中，Δl、Δθ含义分别为目标偏离距离均值与航位角均值的偏差

(4)

由此建立二维平面坐标系下的目标运动分布概率密度函数，设目标在tn时刻位于点(xn,yn)，经过时间Δt后,在tn+1时刻运动到区域R的概率为：

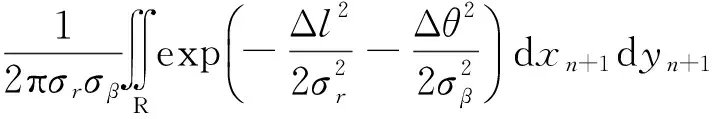
(5)

二维平面坐标系下航位预测目标分布概率与扩散运动目标分布概率如图1～2所示.

图1 扩散运动下目标分布概率Fig.1 Probability of target distribution under diffusion motion

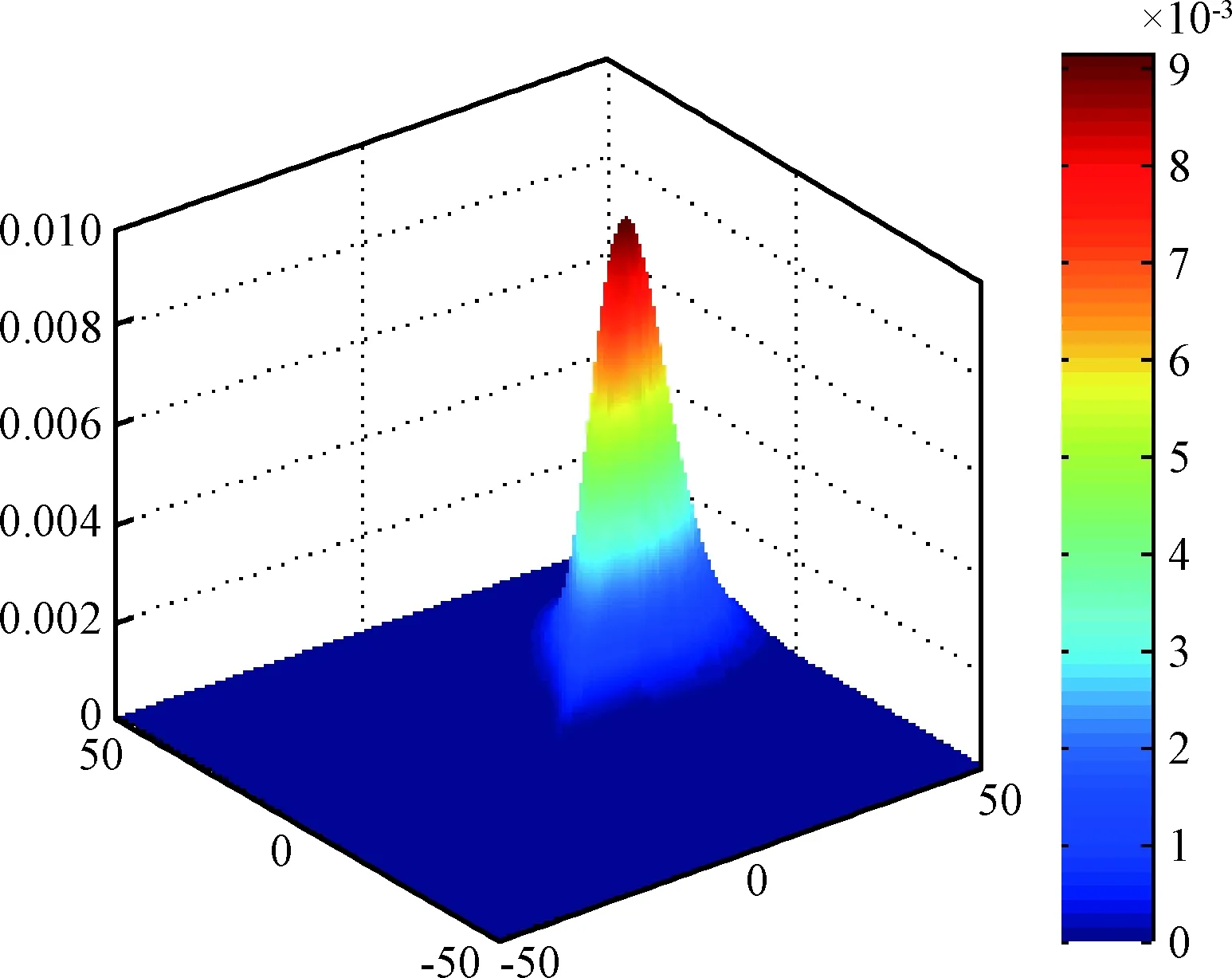
图2 航位预测下目标分布概率Fig.2 Probability of target distribution under sail

图1为文献[5]中建立的目标扩散运动预测模型，图2为先验信息中包含目标运动速度及航向信息的航位预测运动模型.通过分析可知，扩散运动预测模型对先验信息依赖较少，目标潜在运动区域相对目标初始位置呈现均匀扩散分布.航位预测运动模型对先验信息依赖较高但是模型预测相对更为精准，机动目标潜在运动区域相对集中，更方便卫星对其跟踪监视.

1.2 地心固连坐标系下目标运动预测模型

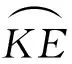
=RE∠POK-V(tn+1-tn)

V(tn+1-tn)

Δθ=∠EKN-∠PKN

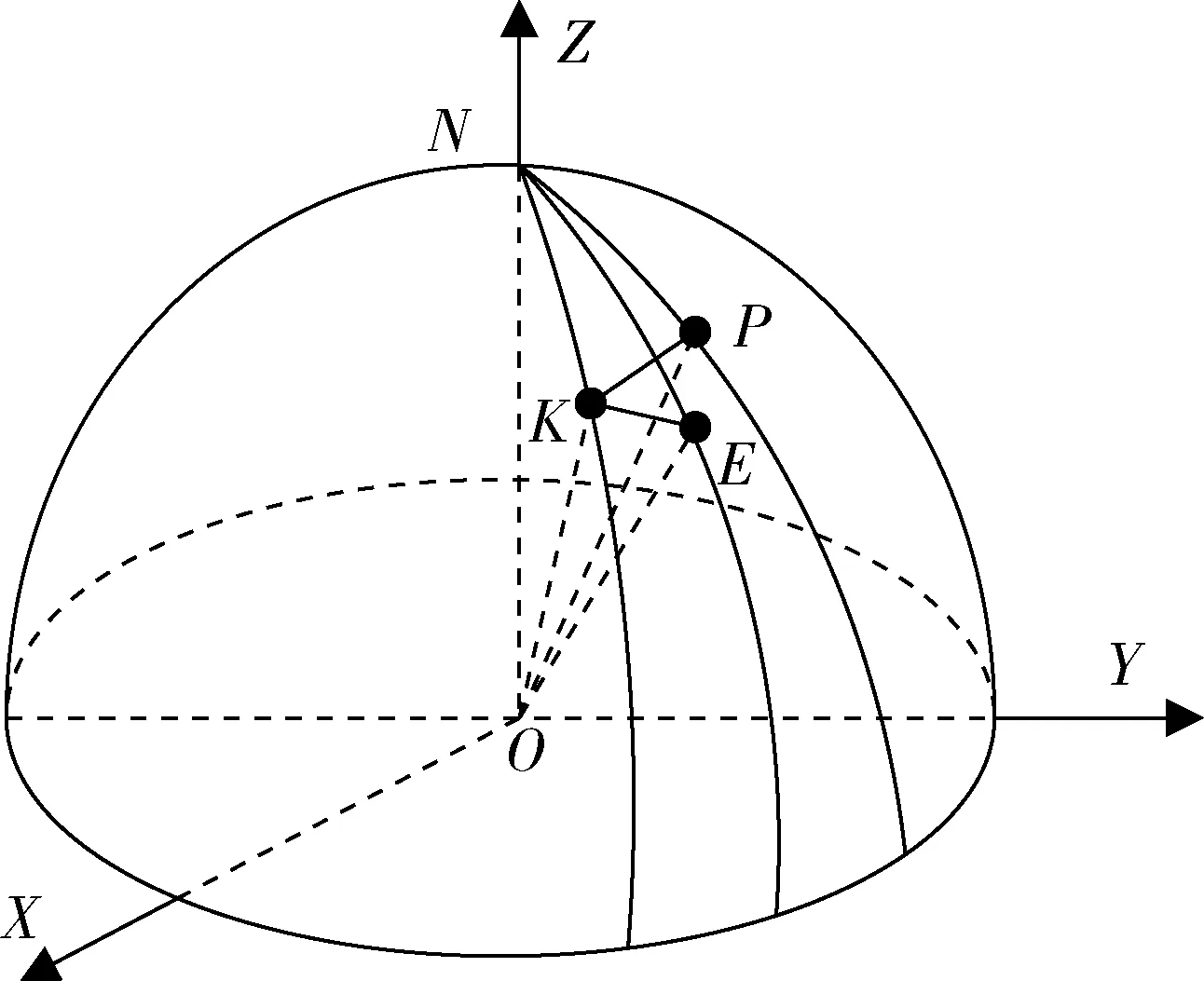
图3 地心固连坐标系下目标运动示意图Fig.3 Target motion diagram

由球面三角形正弦定理可得：

因此可得三维地心固连坐标系下机动目标在tn时刻位置K(xn,yn,zn)运动到tn+1时刻位置P(xn+1,yn+1,zn+1)概率为

(6)

同理，转移到某一区域的目标分布概率可由积分方式求解.

1.3 地理坐标系下目标运动预测模型

由地心固连坐标系下的目标转移概率模型可得，机动目标在tn时刻自位置K(xn,yn,zn)运动到某一球面区域R的目标分布概率为

(7)

当曲面R光滑时，由曲面面积积分公式可得：

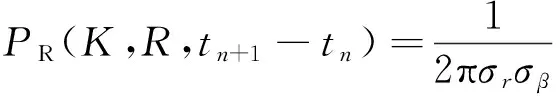
(8)

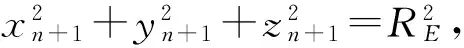
(9)

则地理坐标系下，机动目标在tn时刻自位置K(xn,yn,zn)运动到某一球面区域R的目标分布概率为

(10)

式(10)中相关参数分别为：

(11)

2 基于霍曼转移的卫星机动方式分析

霍曼转移变轨方式最节省卫星燃料，其调整卫星相位的原理是：利用转移轨道与初始轨道的周期不同改变卫星相位角度，变轨之前与变轨之后卫星都在同一轨道运行，不影响卫星载荷使用.当卫星施加一个速度冲量Δv之后，卫星进入转移轨道，由于转移轨道与初始轨道半长轴不同，因此卫星在转移轨道运行一个或多个周期之后会与初始轨道产生一个相位差，从而实现相位改变，根据施加冲量的方向不同(顺卫星运行方向与逆卫星运行方向)分为超前相位调节与滞后相位调节.在超前相位调节中，施加冲量与卫星运行方向相反，卫星减速进入转移轨道，因转移轨道周期相对初始轨道要小，在转移轨道运行一周后回到转移点，此时若卫星在初始轨道运行，还未到达转移点，从而实现相位超前.在滞后相位调节中，施加冲量与卫星运行方向相同，卫星加速进入转移轨道，转移轨道相对初始轨道周期大，卫星运行一周后，此时若在初始轨道运行，已经越过转移点，从而实现相位滞后.两种不同相位机动调整方式如图4～5所示.

图4 超前相位调节Fig.4 Advance phase regulation

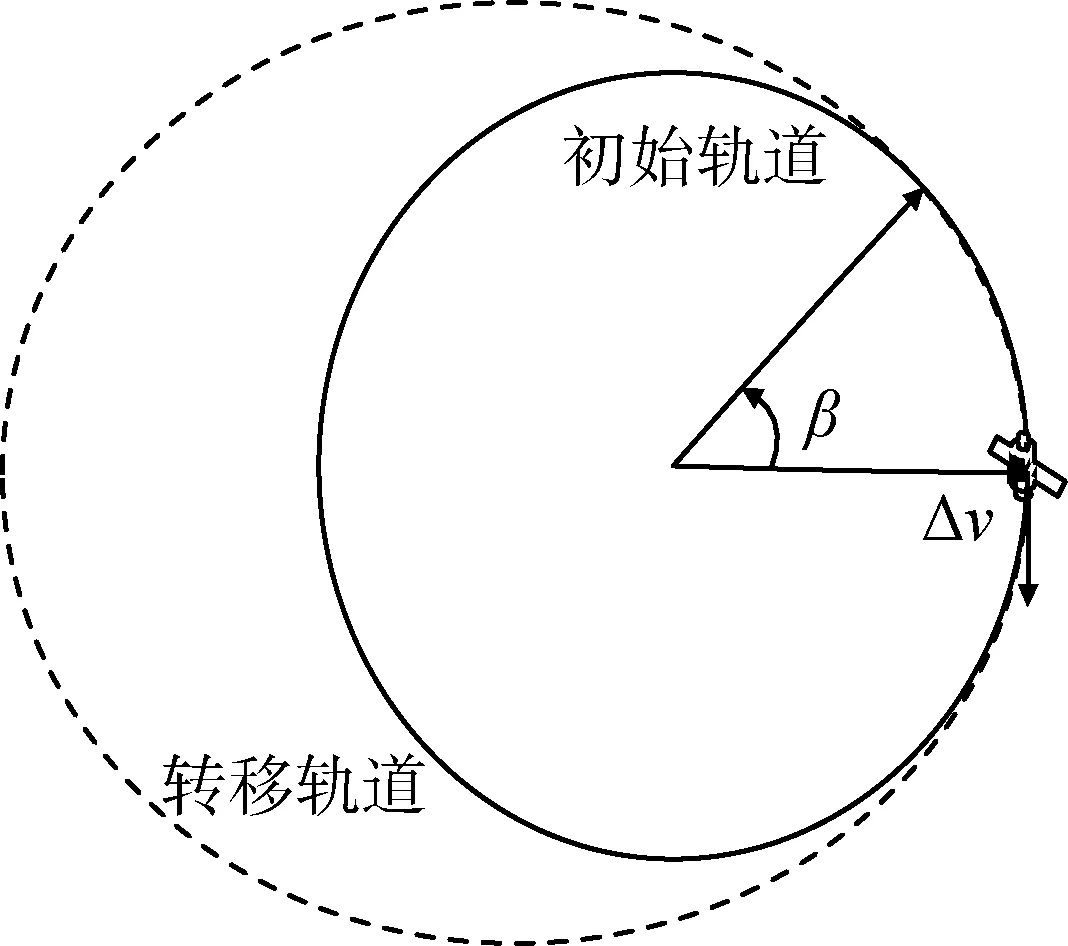
图5 滞后相位调节Fig.5 Lag phase regulation

在超前相位调节中，设初始轨道半长轴为a0，转移轨道半长轴为a1，则卫星在转移轨道上运行一圈相位超前角θ为：

θ=2π-n0T1

则

(12)

式中，n0、n1为初始轨道平均角速度与转移轨道平均角速度，T1为转移轨道周期，μ为地球引力常数，μ=3.986 004 415×1014m3/s2.

在超前相位调节中，初始轨道与终轨道均为同一圆轨道，转移轨道为椭圆轨道，首先对卫星逆向施加速度冲量Δv，使得卫星从初始轨道转移到椭圆轨道.卫星在运行至转移点后，顺向再次施加Δv，使得卫星回到初始轨道完成变轨，由于两次变轨施加的速度冲量Δv绝对值相同，且根据齐奥尔科夫斯基公式[6]，假设燃料消耗与Δv绝对值大小成正比.因此在超前相位调节中，所需能量消耗为

(13)

滞后相位调节是先对目标卫星加速，再对卫星减速进行相位调节，其数学模型与超前相位调节基本一致.由此计算滞后相位调节中，卫星在转移轨道运行一圈机动的相位角β与所需的速度增量为

(14)

由此根据初始轨道与转移轨道的半长轴大小得出相位调节的超前角度α或滞后角度β，以及相应的转移消耗能量J，由于卫星轨道高度受到范艾伦辐射带及大气阻力的影响，近地卫星轨道高度通常有上限与下限，根据本节所建立的相位角调整模型可知，在转移轨道一个周期内卫星具有最大超前相位调节角度maxθ及最大滞后相位调节角度maxβ.当所需调节相位超过maxβ或maxθ时，则不能再通过改变转移轨道半长轴来进行调节，而需要卫星在转移轨道运行多个周期以满足相位调节角度，受响应时间的约束要求，卫星转移时间nT1≤tMORT，tMORT为任务响应时间，并且还要预留出充分的卫星姿态稳定时间来满足成像约束需求.

根据范艾伦辐射带及大气阻力对近地轨道卫星的影响[7]，将卫星转移轨道高度限制在[200,1 500]km，由式(13)～(14)可得单个转移轨道周期内超前相位调节与滞后相位调节最大可调节角度及能量消耗关系，如图6～7所示.由图6分析可知，在单个轨道周期内，随着轨道高度的增加，超前相位调节最大可调节角度maxθ在[4°，29°]范围内逐渐增加，滞后相位调节最大可调节角度maxβ在[18°，50°]范围内逐渐降低.单个轨道圈次内卫星可调节相位范围是有限的，若要考虑对卫星进行大范围相位调节，则需要进行多个圈次相位调节.

图6 轨道高度与最大相位调节角度关系Fig.6 The relationship between orbit altitude and phase angle adjustment

图7 轨道高度与最大能量消耗关系Fig.7 The relation between orbit altitude and energy consumption

3 面向机动目标跟踪监视的卫星重构组网设计与优化

3.1 目标函数与决策变量空间

在对卫星重构组网观测前后，都需要对卫星进行合理任务规划，筛选最优观测条带与开机关机时间[8].文献[5]建立了针对机动目标搜索的MDPA算法(最大目标发现概率算法).需要注意的是MDPA算法是针对在轨卫星任务规划，通过优选卫星过境观测条带实现对机动目标的最大发现概率.在本文中若直接采用MDPA算法，在每一种调相组网情况下，卫星都会有多个侧摆角度可供选择，容易造成搜索空间急剧增大.因此重构调相组网情况下，决策变量空间需要加入机动卫星的真近地点角.组网优化的目标函数主要为目标发现概率与机动能量消耗，采用重构调相方式进行组网搜索机动目标时，主要目的是采用最小能量消耗换取最大目标发现概率，因此将目标函数描述如下：

1)MaximizeP(tn)最大化时刻目标发现概率；

2)Minimize(J)最小化卫星机动能量消耗.新增决策变量为备选重构卫星相位角，其变量范围为n[-maxβ,maxθ]，其中maxβ、maxθ分别为单个转移轨道周期内最大可调节相位角度，n为转移轨道周期数，可根据任务响应时间及式nT1≤tMORT确定.

3.2 基于NSGA-Ⅱ算法的重构组网求解流程

重构组网搜索机动目标模式下优化变量为备选重构卫星的真近地点角(f1,f2…fn)以及参与机动目标跟踪的卫星侧摆角度(δ1,δ2…δn)，根据用户对响应时间的要求，可以确定卫星重构组网时最大转移轨道运行圈数n，利用非支配快速排序遗传算法NSGA-Ⅱ求解重构组网模型的流程如下：

1)(参数初始化)：种群规模NP，交叉概率CR，进化代数GNmax，仿真周期、搜索资源参数以及监视目标场景信息采用随机均匀分布在决策变量空间内生成NP个染色体xi(g)；

2)根据目标函数值对初始种群进行基于Pareto的非支配排序，将排序后初始种群的最优前沿作为外部存档EA；

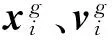
式中，Pc表示交叉概率，Pc∈(0,1)，r为(0,1)上的随机数，CR表示交叉操作.

5)判断是否达到最大迭代次数Itermax，如果达到，则输出外部存档EA作为Pareto非劣解集，并对解集的收敛性、均匀性、多样性进行评价，如果没有达到，则重复步骤步骤3～5.

4 仿真试验分析

仿真试验背景设计：2020/01/01 09:00:00在(40.6N,146.3E)位置发现舰船，其当前行进速度为40 km/h，行进方向与正北方向夹角为60°，在一定时间内舰船速度变化值为±20 km/h，方向角改变最大值为±36.8°.要求在初次发现目标后五小时内对其进行跟踪监视.仿真试验卫星参数参照美国”数字全球”公司遥感系列卫星[10]，并设Satellite-1、Satellite-3卫星具有一定机动变轨能力，相关卫星参数如表1所示.

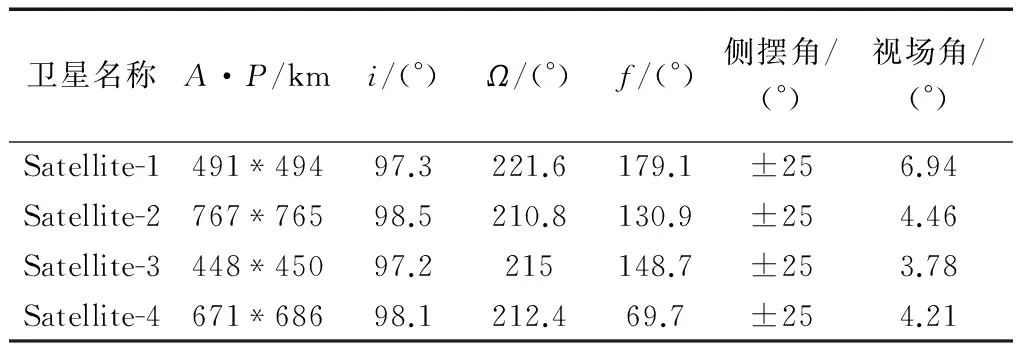
表1 在轨候选卫星参数Tab.1 Basic performance parameters of satellites

仿真时间设为从2020/01/01 00:00:00开始，在进行卫星过境预处理时将卫星视场角设为侧摆范围内可达到角度，通过仿真软件进行轨道预处理得出的卫星对规划周期内机动目标的潜在区域卫星过境时刻表如表2所示：

在不进行机动重构组网情况下，设网格划分经度为0.1，侧摆偏移步长为0.5°采用MDPA算法[4]求解得到的仿真结果如表3所示：

由表3仿真结果可以看出，Satellite-1与Satellite-2过境时间相邻，并且能够较好的覆盖到目标潜在运动区域，可观测时间较长，Satellite-3在规划周期内则没有可见窗口，不能有效对机动目标进行跟踪监视，Satellite-4在规划周期内对目标潜在区域过境时间相对较短，能够对目标区域实现部分覆盖观测.采用文献[5]任务规划方法对其进行规划得到的目标发现概率为0.801 3，大于卫星观测条带覆盖率，这是由于目标潜在区域概率分布不均，MDPA算法优先选择概率分布较大的网格区域.下面分析通过卫星重构组网目标跟踪监视情况.

表2 卫星过境预处理Tab.2 Satellite transit preprocessing

表3 基于MDPA算法的目标发现概率Tab.3 Target discovery probability based on MDPA algorithm

由表2可知，在不进行重构组网情况下，Satellite-1、Satellite-2以及Satellite-4可通过在轨任务规划实现对机动目标潜在区域覆盖，考虑卫星机动情况将有损卫星在轨运行寿命，只对Satellite-3进行相位机动调整，由3.1小节可知决策变量空间为f3,θ1,θ2,θ3,θ4，目标函数为MaximizeP(tn)、Minimize(J).采用非支配快速排序遗传算法NSGA-II得到的Perato前沿如图8所示.

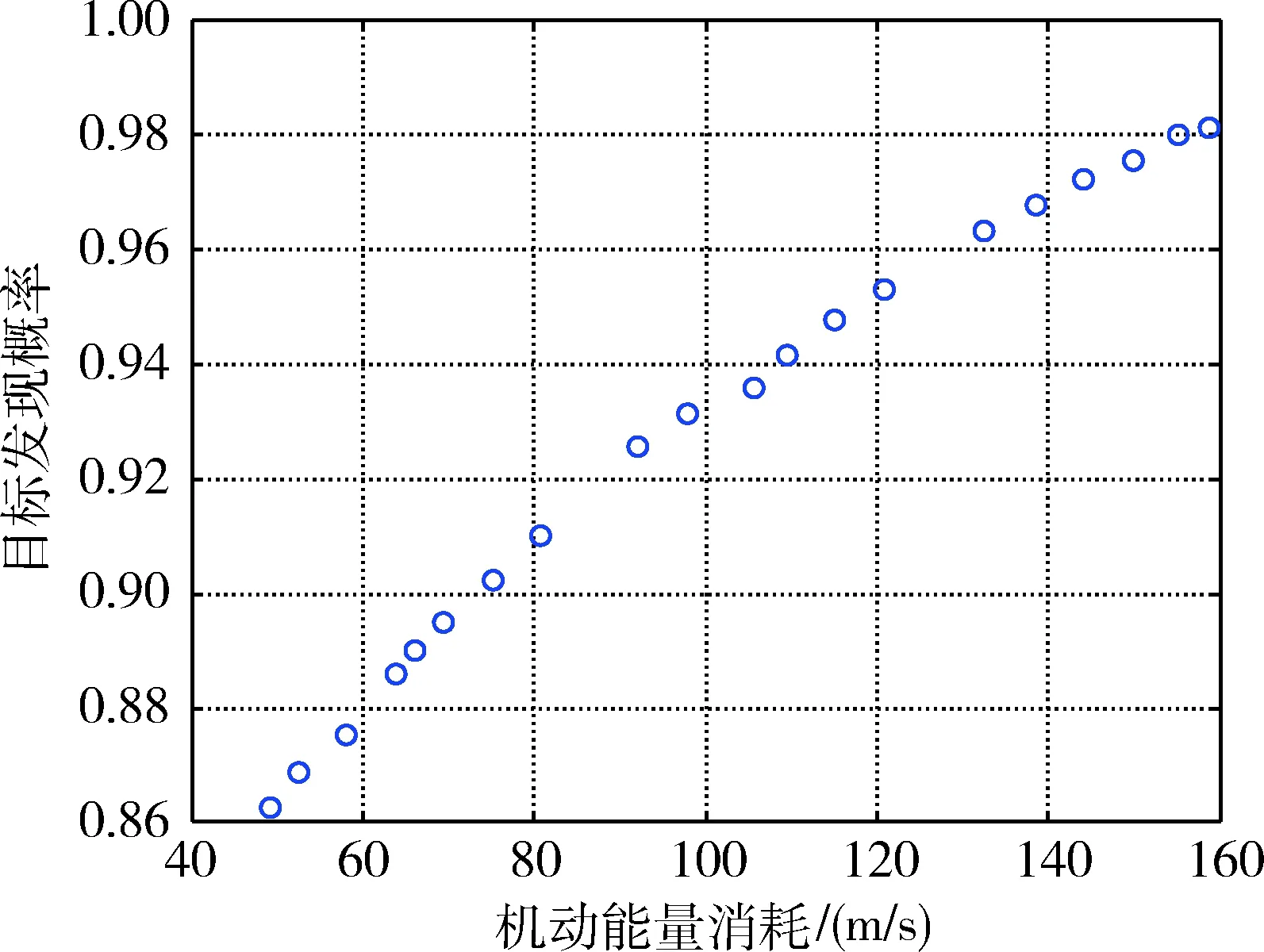
图8 重构组网Pareto前沿分布Fig.8 Pareto frontier distribution

由图8分析可知，随着机动能量消耗的增大，机动目标发现概率也逐渐增大.从理论上分析，随着机动能量消耗的增加，卫星相位调节角度相应增大，卫星对机动目标潜在区域可覆盖范围增大，可选观测条带增多，能够更好的对机动目标进行搜索监视.图8 中Satellite-3机动能量消耗在49.156～158.661 m/s 内，相应的目标发现概率为0.862 5～0.981 2，相比未进行调相情况下目标发现概率提升了7.6%～22.5%，有效的提升了机动目标发现概率.在实际工程运用中，受卫星星上燃料限制，可根据星上燃料情况采取适当机动方式，在卫星寿命允许情况下对机动目标进行搜索监视.

5 结 论

本文针对海洋机动目标搜索跟踪监视问题，提出了基于卫星重构调相组网的机动目标搜索策略，构建了地理坐标系下机动目标航位预测模型并采用NSGA-II算法进行求解，通过仿真算例可以看出：卫星进行重构组网能够有效提升机动目标发现概率，并且在一定范围内，机动能量消耗与目标发现概率呈正相关，在实际工程运用中，可根据实际需求和决策者偏好，寻找两者平衡点，在具有较高机动目标发现概率的同时，用较小的能量消耗完成卫星相位机动调整.研究内容为海洋机动目标跟踪监视提供了一种可行且有效的途径，具有一定的应用价值意义.

参 考 文 献

[1] 李智，张占月，孙琰.现代太空战[M].北京：国防大学出版社，2016:201-215.

[2] 陈杰,邢利菊.面向海洋移动目标成像侦察方法研究[J].计算机与数字工程,2014,42(3):395-398.

CHEN J,XING L J.Imaging reconnaissance method facing ocean motion target[J].Computer and Digital Engineering,2014,42(3):395-398.

[3] 朱冬骏,张占月,赵程亮,刘瑶.一种实现光学隐身的卫星构型设计[J].空间控制技术与应用,2017,43(1):61-66.

ZHU D J,ZHAO Z Y,ZHAO C L,LIU Y.A satellite configuration design for optical stealth[J].Aerospace Control and Application,2017,43(1):61-66.

[4] BERRY P E, PONTECORVO C,FOGG D.Optimal search, location and tracking of surface maritime targets by a constellation of surveillance satellites[R].Dsto Information Sciences Laboratory,DSTO-TR-1480, 2003.

[5] 徐一帆. 天基海洋移动目标监视的联合调度问题研究[D].国防科学技术大学,2011:40-63，74-125.

[6] 胡其正，杨芳.宇航概论[M].中国科学技术出版社，2010：116-117.

[7] 吴正午,任华,蒋昊东.区域侦察小卫星星座设计与仿真[J].计算机仿真,2015,32(2):87-91.

WU Z W，REN H，JIANG H D.Regional reconnaissance satellite constellation design and simulation[J].Computer Simulation,2015,32(2):87-91.

[8] XU R, CHEN H,LIANG X,et al. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization[J].Expert Systems with Applications, 2016, 51: 195-206.

[9] TASGETIREN M F,SUGANTHAN P N,PAN Q K.An ensemble of discrete differential evolution algorithms for solving the generalized traveling salesman problem[J].Applied Mathematics and Computation, 2010, 215(9):3356-3368.

[10] 李颖,杨庆,卢雪.国外典型航天系统手册[M].北京：国防工业出版社, 2016:10-24.