一种基于模糊分割的黄金分割控制器设计及其应用*

冯佳佳，李宜鹏

0 引 言

对于阶数及参数未知的多输入-多输出高阶非线性系统，如何设计一个工程上易于实现的低阶控制器，以达到高性能控制要求，这是目前航天等领域急待解决的问题[1].复杂航天器具有挠性结构，还有液体晃动和消耗，同时对控制能力的要求又很高，即要求高精度、高稳定度、高灵敏度的控制性能，以及鲁棒适应性和长寿命可靠性等[2]，因此急需发展智能自主控制[3-5].

基于特性模型的智能自适应控制方法是吴宏鑫院士1992年提出的，主要包括特征建模理论和方法、黄金分割自适应控制方法等内容[6-7].黄金分割自适应控制律是将黄金分割与最小方差自适应控制律相结合的一种新的自适应控制方法，在一定条件下，可以保证参数未收敛于“真值”时闭环系统的稳定性以及对未建模误差的鲁棒稳定性[8].由于此控制律中的系数是通过系统实时辨识得到，当被控对象为强非线性、强时变特性时，系统的辨识效率并不是很理想.而模糊逻辑控制[9-11]可以有效地对系统辨识的区域进行规划，从而有效地提高辨识效率，使系统的控制性能不断改善，以致达到最佳的控制效果[12].因此，模糊逻辑控制与黄金分割控制的有效结合，有望进一步提高系统的控制效果.关于模糊控制与特征模型相结合的思想，文献[1]提出一种基于特征模型稳定的自适应模糊广义预测控制方案；文献[13]提出一类基于特征模型的快速模糊自适应控制器设计方法;文献[14]提出一种面向空天飞行器的模糊动态特征建模与控制方法.而本文在总结前面文献的基础上，给出了一种基于模糊分割的黄金分割控制器(以下简称模糊黄金分割控制器)的详细设计过程，并从理论上证明了模糊黄金分割控制器的稳定性，最后将模糊黄金分割控制应用到小卫星[15-17]的姿态机动控制中.

其中，模糊黄金分割控制器的结构框图如图1所示，它通过对非线性状态空间进行模糊分割，对每个模糊子系统分别设计黄金分割控制律，然后整个非线性系统的控制取为各个模糊子系统黄金分割控制的加权和.

图1 基于特征模型的模糊黄金分割控制框图Fig.1 Fuzzy golden section controller based on characteristic model

1 问题描述

考虑小卫星姿态的快速机动及稳定控制方法.动力学模型可以描述为[18]:

(1)

定义卫星欧拉姿态角q(t)=[φθψ]T，其中φ，θ，ψ分别为航天器的滚动、俯仰和偏航角，其角速度在星体坐标系中的表达式为：

(2)

其中，当q在一定区间变化时，B(q)是可逆阵，本文只研究B(q)可逆的情况.

当采用1-2-3转序时，

(3)

2 模糊黄金分割控制器设计

2.1 特征建模方法

所谓特征建模就是根据对象动力学特性、环境特性和控制性能要求相结合来建模，与传统动力学建模的最大区别是结合控制性能要求建模[6].

工程上常见的线性定常高阶对象

(4)

可以利用一个二阶慢时变差分方程来表示，即

yk+1=f1,kyk+f2,kyk-1+g0,kuk

(5)

令：

(6)

其中，递推最小二乘为

(7)

此时，黄金分割控制器设计为：

(8)

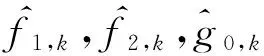
2.2 模糊黄金分割控制器设计

其基本思想是将n维非线性状态空间模糊分割为个模糊子空间，对每个模糊子空间，分别设计一个基于特征模型的黄金分割控制器，然后将整个非线性系统的控制取为各个模糊子系统黄金分割控制的加权和.

首先，对n维非线性状态空间模糊分割为l个模糊子空间.需要说明的是，关于模糊分割通常情况下可以采用均匀分割的方法，但一般情况下，应根据模型特性，对于不同的区域采用不同粒度的分割，其原则是当模型特性变化比较剧烈时应分割得细一点，模型特性变化比较平缓时应分割得粗一点，而隶属度函数通常取对称形式[19].

非线性状态空间模糊分割后，产生l条T-S模糊规则，而在第i条T-S模糊规则下，被控对象的模糊特征模型可以表示为：

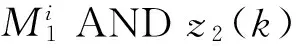
则：

对第i条T-S模糊规则进行归一化，则归一化后的发放强度为：

此时，在l条T-S模糊规则下，整个被控系统的特征模型可表示为

(9)

令：

(10)

则由式(7)可以计算得到各个参数.

针对第i条T-S模糊规则

所以整个非线性系统的控制律为：

(11)

其中，μi(x)为归一化发放强度.

2.3 模糊黄金分割控制稳定性证明

引理1.对于任一n阶对象G(s)，在满足一定采样周期Δt的条件下，当要实现位置保持或位置跟踪控制时，其特征模型可用一个二阶时变差分方程形式来描述[6]

y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k)

(12)

由式(9)可知：

=ykf1+yk-1f2+ukg0

(13)

因此，非线性状态空间进行模糊分割后，整个被控系统的特征模型满足特征建模原理.

引理2.被控对象的离散后的差分方程为：

y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k)

对象系数f1(k),f2(k),g0(k)未知，并在一定的闭凸集Ds之内，控制器为：

由式(11)得

(14)

所以式(14)得：

(15)

由引理2可知，式(11)所示的控制律是稳定的.也就是说，针对黄金分割控制律稳定的系统，模糊黄金分割控制律仍然稳定.

3 仿真校验

为了验证模糊黄金分割的有效性，进行数学仿真：

卫星的转动惯量为

挠性帆板一阶频率为2.23 Hz，阻尼为0.005，耦合系数矩阵为diag{0.000 41,3.833,0}；

干扰力矩为

采样时间为t=0.01 s，控制力矩采用0.1 N·m的限幅.

针对姿态的控制目标，现对3个姿态(即φ，θ，ψ)进行模糊分割，为便于分析和计算，将模糊状态区域划分为两个模糊子区域：即“初始区域”，“目标区域”两个区域.划分后3个姿态角分别对应子区域的中心点为：|φ|=0和π/6，|θ|=0和π/12，|ψ|=0和π/18，隶属度函数均取于三角形函数，其分别对应的隶属度函数图形如图2所示.

图2 隶属度函数曲线Fig.2 Membership function curves

仿真结果如图3～8所示.其中，图3～5为卫星姿态机动时，模糊黄金分割控制和黄金分割控制的系统参数辨识曲线，图6为3个姿态角分别在模糊黄金分割控制、黄金分割控制和PID控制作用下的波形曲线，图7为3个姿态角速度分别在模糊黄金分割控制、黄金分割控制和PID控制作用下的波形曲线，图8为3个控制力矩分别在模糊黄金分割控制、黄金分割控制和PID作用下的波形曲线.

图3 滚动轴机动时参数辨识曲线Fig.3 Identification curves of roll maneuver

图4 俯仰轴机动时参数辨识曲线Fig.4 Identification curves of pitch maneuver

图5 偏航轴机动时参数辨识曲线Fig.5 Identification curves of yaw maneuver

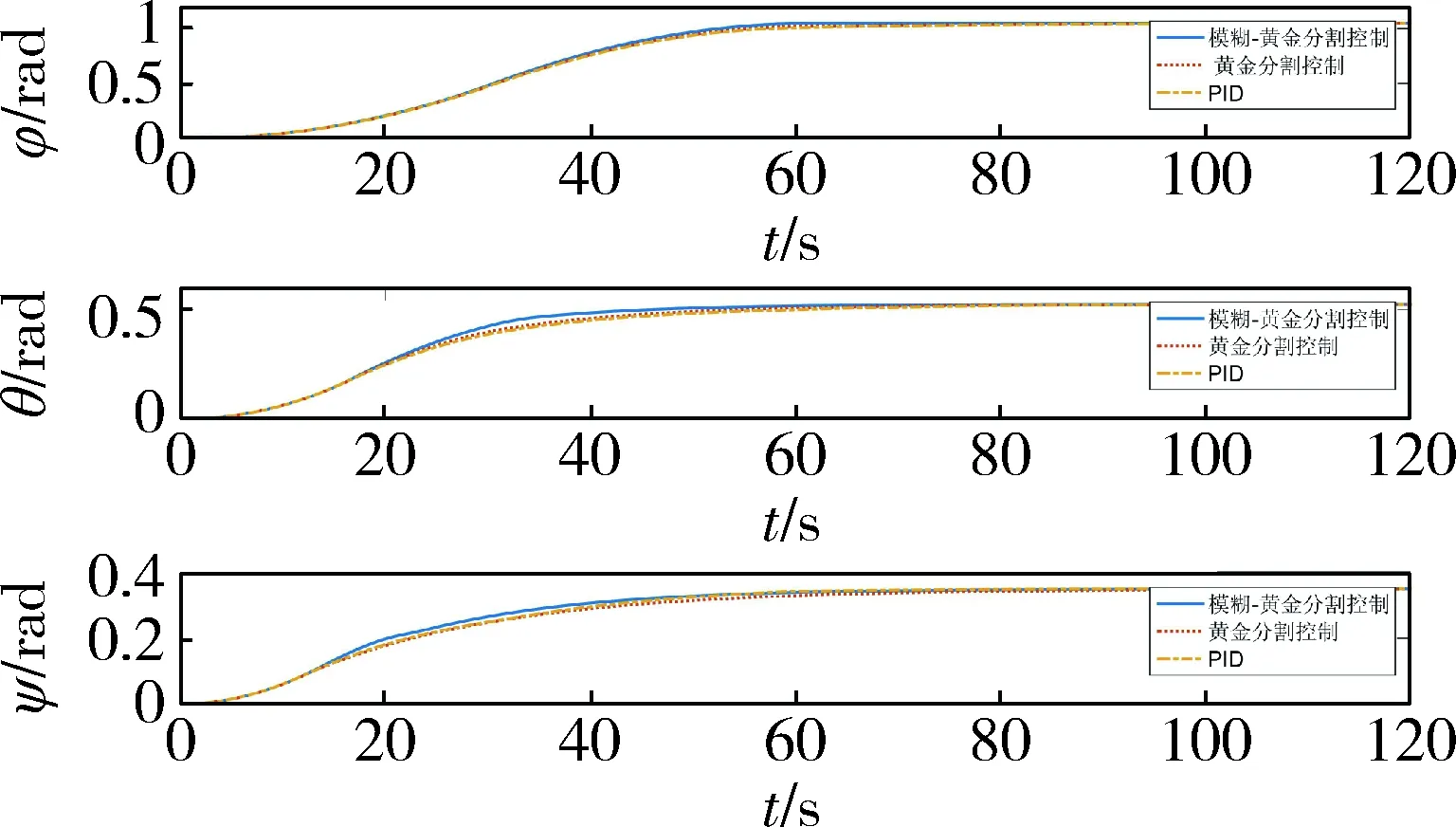
图6 卫星姿态角Fig.6 Satellite attitude angulars

图7 卫星姿态角速度Fig.7 Satellite attitude angular velocities

图8 卫星控制力矩Fig.8 Satellite control moments

从图3～5可以看出，当卫星做姿态机动时，在姿态机动初始阶段，模糊黄金分割控制的两个模糊子空间中的系统辨识参数在随时间进行变化，这表明两个模糊子空间的黄金分割控制律均起到作用.从图6～8可以看出，在卫星姿态机动时，模糊黄金分割控制的姿态机动时间优于黄金分割控制和PID控制，并且在控制力矩变化上，模糊黄金分割控制的波动频率相对较小.

4 结 论

模糊黄金分割控制是将模糊控制和黄金分割控制相结合的一种智能控制方法，它通过对非线性状态空间进行模糊分割，降低特征建模的难度，有效地提高系统的辨识效率，从而提高系统的控制性能，该方法可以有效的完成小卫星的姿态机动，且具有良好的控制精度和鲁棒性，因此模糊黄金分割控制具有一定的应用价值.但模糊黄金分割控制在设计过程中比黄金分割控制相对复杂，需要对非线性状态空间进行模糊分割以及对每一个模糊子空间分别进行黄金分割控制器的设计，因此有待进一步优化.

参 考 文 献

[1] 孙多青，吴宏鑫.多变量线性时变系统的特征模型及自适应模糊控制方法[J].宇航学报，2005, 26(6): 677-681.

SUN D Q,WU H X.Characteristic modeling and adaptive fuzzy control method of MIMO higher-order linear time-varying systems [J]. Journal of Astronautics, 2005, 26(6):677-681.

[2] 吴宏鑫.工程实际中的控制理论和方法的研究与展望[J].控制理论与应用，2014, 31(12): 1626-1631.

WU H X. Research and prospect on the control theory and method in the engineering[J].Control Theory & Applications,2014,31(12):1626-1631.

[3] 吴宏鑫，胡军，解永春.航天器智能自主控制研究的回顾与展望[J].空间控制技术与应用，2016,42(1):1-6.

WU H X, HU J, XIE J C. Spacecraft intelligent autonomous control: past, present and future[J]. Aerospace Control and Application, 2016, 42(1):1-6.

[4] 李智斌.航天器智能自主控制技术发展现状与展望[J].航天控制，2002,20(4):1-7.

LI Z B. Current situation and prospective of intelligent autonomous control for spacecraft[J].Aerospace Control,2002, 20(4):1-7.

[5] 吴宏鑫,谈树萍.航天器控制的现状与未来[J].空间控制技术与应用，2012,38(5):1-7.

WU H X,TAN S P.Spacecraft control: present and future[J].Aerospace Control and Application, 2012, 38(5):1-7.

[6] 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制[M].北京：中国科学技术出版社，2009.

WU H X,HU J,XIE Y C.Characteristic model based intelligent and adaptive control[M].Beijing: China Science and Technology Press, 2009.

[7] 吴宏鑫.全系数自适应控制理论及其应用[M].北京：国防工业出版社，1990.

WU H X. All-coefficient adaptive control theory and application[M].Beijing:National Defense Industry Press, 1990.

[8] 解永春，吴宏鑫.黄金分割在自适应鲁棒控制器设计中的应用[J].自动化学报，1992,18(2): 177-185.

XIE Y C,WU H X.Application of the golden section control in the adaptive and robust control design[J]. Acta Automatica Sinica,1992,18(2):177-185.

[9] ZADEH L A.Fuzzy sets[J].Information and Control, 1965,8:338-353.

[10] LEE C C.Fuzzy logic in control system:fuzzy logiccontroller;PartⅠ,Ⅱ[J].IEEE Trans. on Systems, Man and Cybernetics, 1990, 20(2):404-435.

[11] PHAN P A,GATE T J.Direct adaptive fuzzy control witha self-structuring algorithm[J].Fuzzy Sets and Systems,2007,159(8):871-899.

[12] 王永富，柴天佑.自适应模糊控制理论的研究综述[J].控制工程，2006,13(3):193-198.

WANG Y F,CHAI T Y.Present status and future developments of adaptive fuzzy control[J].Control Engineering Of China,2006,13(3):193-198.

[13] 邓建球，张正霞，黎江，等.基于特征模型的快速模糊自适应控制器的设计及应用[J].中南大学学报，2011,42:85-89.

DENG J Q,ZHANG Z X,LI J, et al.Design for fast fuzzy adaptive controller based on characteristic model [J].Journal of Central South University(Science and Technology),2011, 42: 85-89.

[14] LUO X，LI J.Fuzzy dynamic characteristic model based attitude control of hypersonic vehicle in gliding phase[J].Science China Information Science,2011, 54(3):448-459.

[15] RAINER S. Status and trends of small satellite missions for earth observation[J]. Acta Astronautica, 2010, 66(1):1-12.

[16] PRIEDHORSKY W C. The ALEXIS small satellite project: better, faster, cheaper faces reality [J]. Nuclear Science, 1993, 40(4):863-873.

[17] 张召才.美国深挖小卫星潜力，欲提升军事用天能力[J].卫星应用，2015, 2:37-44.

ZHANG Z C.American research small satellites potential,to promote military ability[J].Satellite Application, 2015, 2:37-44.

[18] 屠善澄.卫星姿态动力学与控制[M].北京：中国宇航出版社，2005.

[19] 孙增圻，邓志东，孙再兴.智能控制理论与技术[M].北京：清华大学出版社，2011.

SUN Z Q, DENG Z D, SUN Z Intelligent control theory and technology[M].Beijing: Tsinghua University Press, 2011.

[20] 孟斌，吴宏鑫.黄金分割控制的收敛性和稳定性研究[J].宇航学报，2009, 30(5):2128-2132.

MENG B,WU H X.Convergence and stability of the golden section control[J].Journal of Astronautics, 2009, 30(5): 2128-2132.

[21] 解永春，吴宏鑫.黄金分割在自适应鲁棒控制器设计中的应用[J].自动化学报，1992,18(2):177-185.

XIE Y C,WU H X.Application of the golden section control in the adaptive and robust control design[J]. Acta Automatica Sinica,1992, 18(2):177-185.

[22] 吴宏鑫，王颖，解永春.非线性黄金分割自适应控制[J].宇航学报，2002,23(6):1-8.

WU H X,WANG Y,XIE Y C.Nonlinear golden section adoptive control [J].Journal of Astronautice, 2002, 23(6):1-8.