小展弦比有限厚度舵面颤振特性分析*

秦玉灵，李晓东，张 飞，李长春，宫晓春，高志勇

0 引 言

舵系统是超声速再入飞行器机动飞行过程中对姿态进行控制的重要环节，主要由伺服机构和舵面组成，通过伺服机构驱动舵面偏转，给飞行器施加设定的控制力和控制力矩，稳定现有飞行状态或改变至预定飞行轨迹，从而实现飞行姿态的实时控制和调整.小展弦比有限厚度舵面是武器系统的典型舵面形式，舵面的气动弹性稳定性[1-4]是决定飞行成败的关键，因此在结构设计初期针对飞行设计工况下不同攻角及不同载荷状态开展舵面颤振分析尤为重要，是保证产品研制及飞行成功的关键环节.文献[5]研究了典型温度分布下小展弦比舵面结构模态特性，得到了不同温度分布下单独舵面结构热颤振特性，对不同加载状态下舵面模态特性未予分析.文献[6]提出了解决带燃气舵的导弹舵面颤振分析方法，未考虑不同舵偏角度对结果的影响.文献[7]用CFD/CSD耦合的颤振时域分析方法对带舵面垂尾的风洞模型进行了跨声速颤振特性分析，未考虑舵偏及加载状态的影响.文献[8]用修正的活塞与细长体理论计算了超声速飞行器升力面和机身的非定常气动力，仿真结果证实了方法的可行性.

本文对某小展弦比有限厚度三角舵面颤振特性进行分析，首先建立舵面系统广义动力学方程并在此基础上研究颤振临界边界分析方法，然后开展舵面有限元分析和模态试验确定不同攻角及不同载荷状态下舵系统模态参数，最后通过颤振计算程序分析各工况舵面颤振临界参数，确定颤振临界边界，形成完整的舵面颤振理论分析方法和计算流程，为舵系统结构设计和优化提供支撑.

1 舵系统动力学方程及颤振边界分析

舵面的颤振特性分析主要包含3个方面内容：舵面非定常气动力的确定、系统模态参数的确定、基于模态坐标下系统动力方程的舵系统颤振临界边界确定.参考国内外研究成果，小展弦比有限厚度三角舵面一般采用当地活塞流理论确定舵面非定常气动力[9].

设舵面颤振型态由n个主模态φ叠加而成，即：

(1)

其中，φ=[φ1(x,y)φ2(x,y),…,φn(x,y)]，ξ=[ξ1(t)ξ2(t),…,ξn(t)].

由拉格朗日方程可得模态坐标下舵面广义动力方程为：

(2)

其中，M为各阶模态质量组成的对角阵，i为虚部；Ω为各阶固有圆频率平方组成的对角阵，g为各阶模态损耗因子(即阻尼项)组成的对角阵，QA为广义气动力矢量矩阵，表达式为：

(3)

其中，s+,s-分别表示舵面的上、下表面，μ(x)为舵型切线与x轴夹角的余弦，pm-pL为舵面任意点处的非定常扰动压力，各参数计算如下：

假定舵面舵型方程为H=H(x,y)，则：

(4)

非定常扰动压力值(pm-pL)可按当地活塞流理论由下式给出：

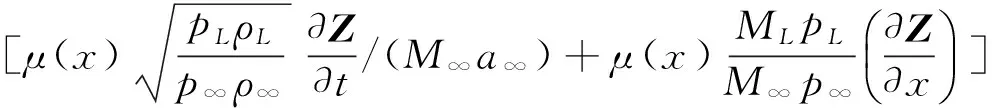
(5)

式中，Z代表舵面微幅振动时中性面挠度方程，p∞、ρ∞、M∞代表舵面远方来流压力、密度和马赫数；pL、ρL、ML代表舵面当地气流压力、密度和马赫数.可通过定常流激波和膨胀波理论确定当地气流参数.

翼型法向流体理论示意图如图1所示，其中Wm为翼型表面微振动产生的附加下洗，VL表示当地流，α∞表示翼面攻角，V∞表示远方来流速度.

图1 翼型法向流体理论示意图Fig.1 Schematic diagram of airfoil normal fluid

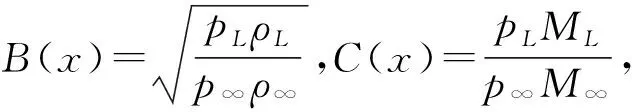
(6)

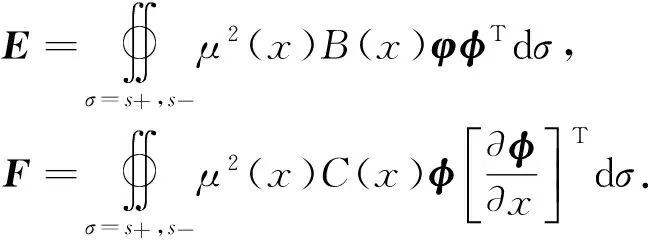
矩阵E、F为对应于模态坐标下的广义气动力系数，令ξ=ξ0eiωt，λ=iω，代入式(2)可得到如下线性特征方程：

(7)

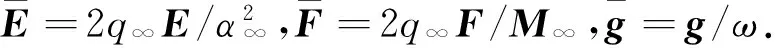
式(7)是一个实矩阵的标准特征值问题，只要给定M∞、q∞和ω，利用广义雅可比法或QR法，即可求出全部复特征根λ=σ+iω*和对应的特征向量.但一般情况下σ≠0，与λ=iω的假设相矛盾，且ω*≠ω.这就要求通过适当的方法导出σ=0和ω*=ω的最小q值，亦即寻找超越函数σ(q,ω)满足ω*=ω的q值最低的零点问题.满足上述条件的动压q和对应的频率ω值即是颤振临界动压qcr和临界频率ωcr.据颤振临界动压与飞行马赫数关系绘制颤振临界边界曲线，确定颤振安全区和危险区，可为舵系统结构设计和分析提供参考.

2 舵面模态有限元分析及模态试验

舵面模态参数的获取通过有限元分析和模态试验结合的方式获取.有限元分析可对模态试验结果进行预示，同时模态试验结果又可作为有限元模型精细化修正的依据，两者互为补充，共同为舵面颤振分析提供数据支撑.

2.1 舵面模态有限元分析

舵面及舵轴有限元建模过程中采用十节点四面体单元，划分为380 161个单元，共655 397个节点.舵机对舵面支撑采用在连接部位建立多点约束MPC形式，模拟实际支撑形式共设立3个MPC，并用Grounded Bush连接单元模拟舵系统刚度，局部连接采用glue模拟.有限元分析过程中据模态试验得到的实际振型，不断调整Grounded Bush连接刚度及glue区域范围，最终得到接近模态试验结果的有限元分析模型.

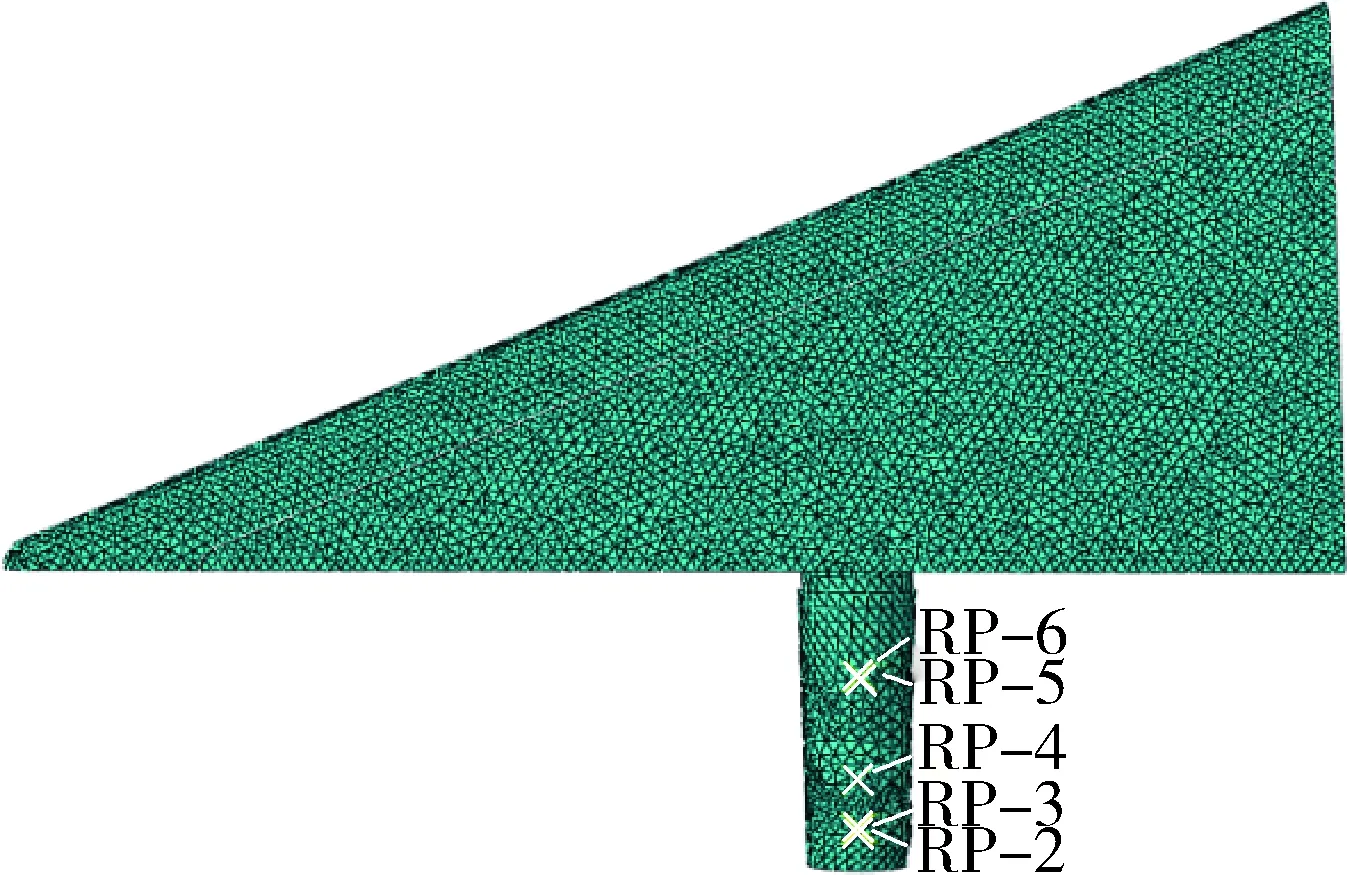
图2 舵面有限元模型Fig.2 Rudder finite element model

2.2 舵面模态试验

舵面模态试验目的是测量舵面-伺服机构在闭环工作状态下的模态参数，包含模态频率、振型、阻尼比和模态质量等，为舵系统颤振特性分析提供模态模型.试验采用固支边界并通过激振器对舵面激振的方式测量舵面模态，试验过程中伺服系统闭环工作使舵面保持规定舵偏角.模态试验过程中采用加速度传感器测量舵面振动响应，测点布置情况如图3所示，测点数量和位置应能有效识别舵的模态，并为颤振分析提供模态参数.

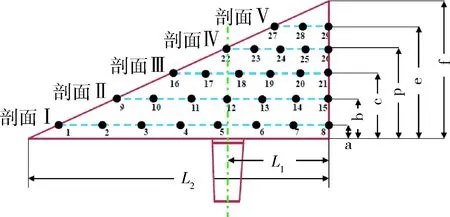
图3 舵面模态试验测点分布示意图Fig.3 Measure point distribution in modal test

为研究无舵偏和有舵偏状态下不同舵偏角对舵面颤振特性影响，试验过程中据使用工况将舵偏角设定为0°和15°两种舵偏状态；为研究伺服传动系统间隙对颤振特性影响，获取舵模态参数变化范围，每种舵偏状态又分为无载和有载两种加载状态考核.由此，舵面模态试验分4种工况进行，即0°舵偏无载工况，0°舵偏有载工况，15°舵偏无载工况，15°舵偏有载工况.各有载工况施加载荷均为500 N，目的是消除传动系统间隙.

舵面模态试验及有限元分析结果如表1所示，扭转和弯曲模态振型图如图4～7所示.可知，有限元分析所得舵面模态频率和振型与模态试验吻合良好，各频率误差均在2%以内.

由表1可知，舵偏角度相同的情况下，有载工况模态频率明显高于无载工况频率；加载工况相同的情况下，小舵偏工况模态频率明显高于大舵偏工况频率.原因在于舵偏角度相同时，有载工况下舵面传动系统间隙明显减小，刚度提高，故模态频率提高；加载工况相同时，小舵偏工况下舵面传动系统间隙小，刚度高，故模态频率高于大舵偏工况.

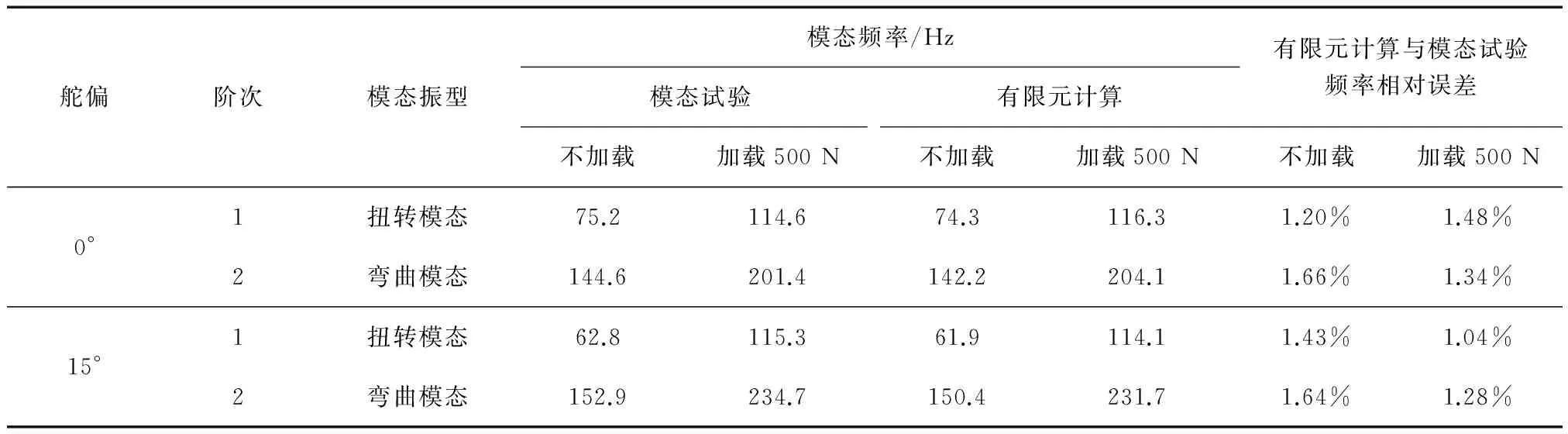
表1 舵面模态试验及有限元分析结果Tab.1 Rudder modal test results

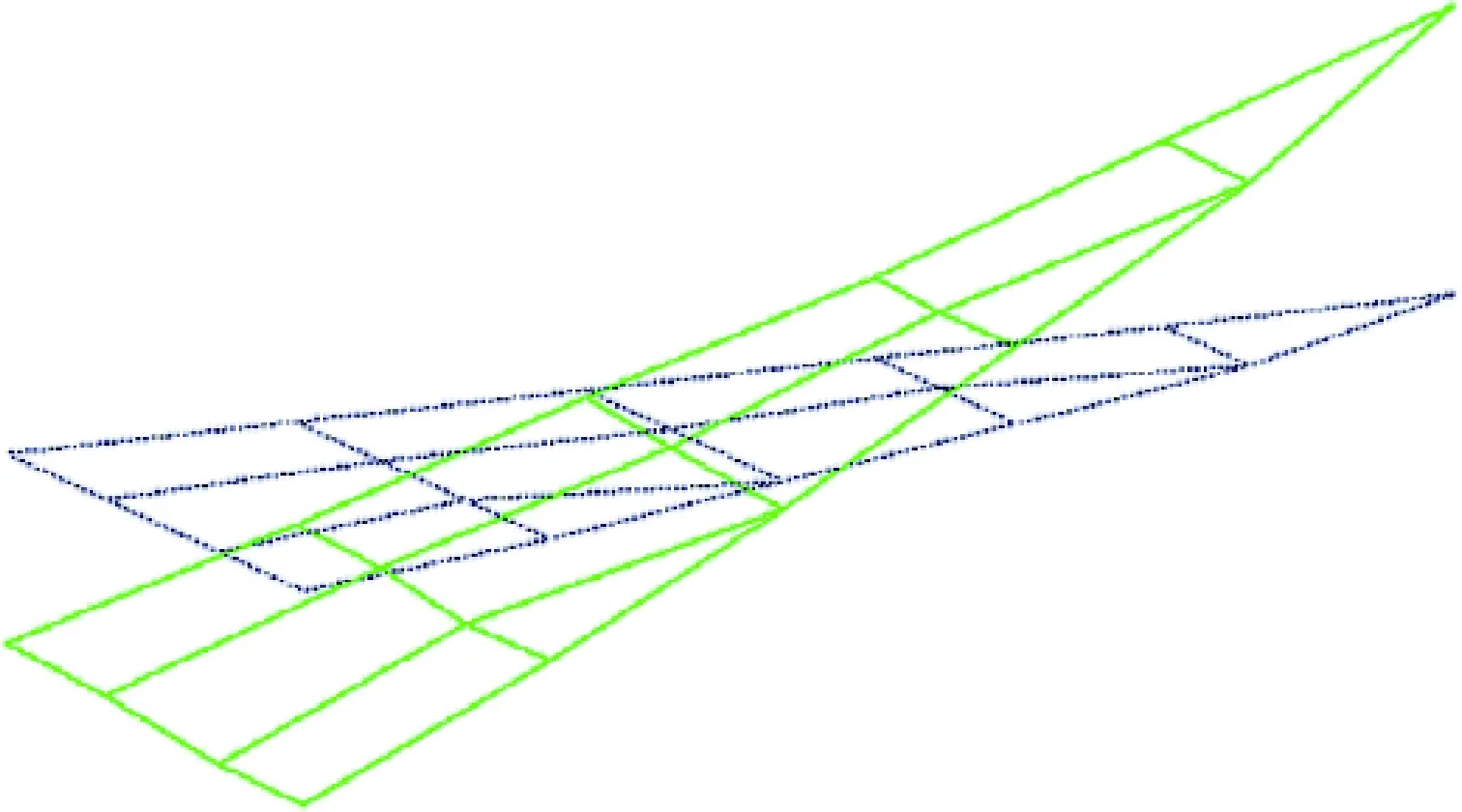
图4 试验一阶振型图(扭转)Fig.4 The first order twisting mode by test

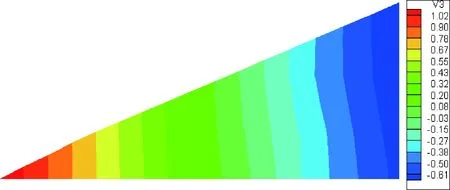
图5 有限元分析一阶振型图(扭转)Fig.5 The first order twisting mode by FEM

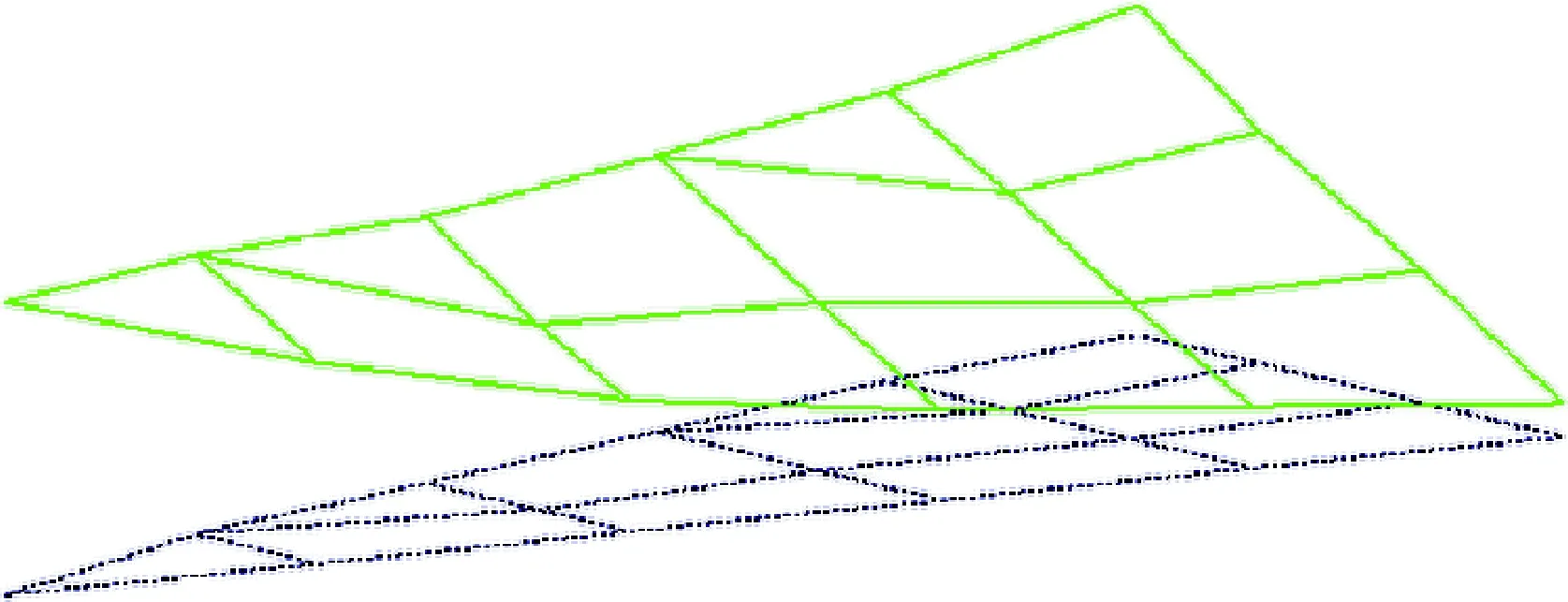
图6 试验二阶振型图(弯曲)Fig.6 The second order bending mode by test

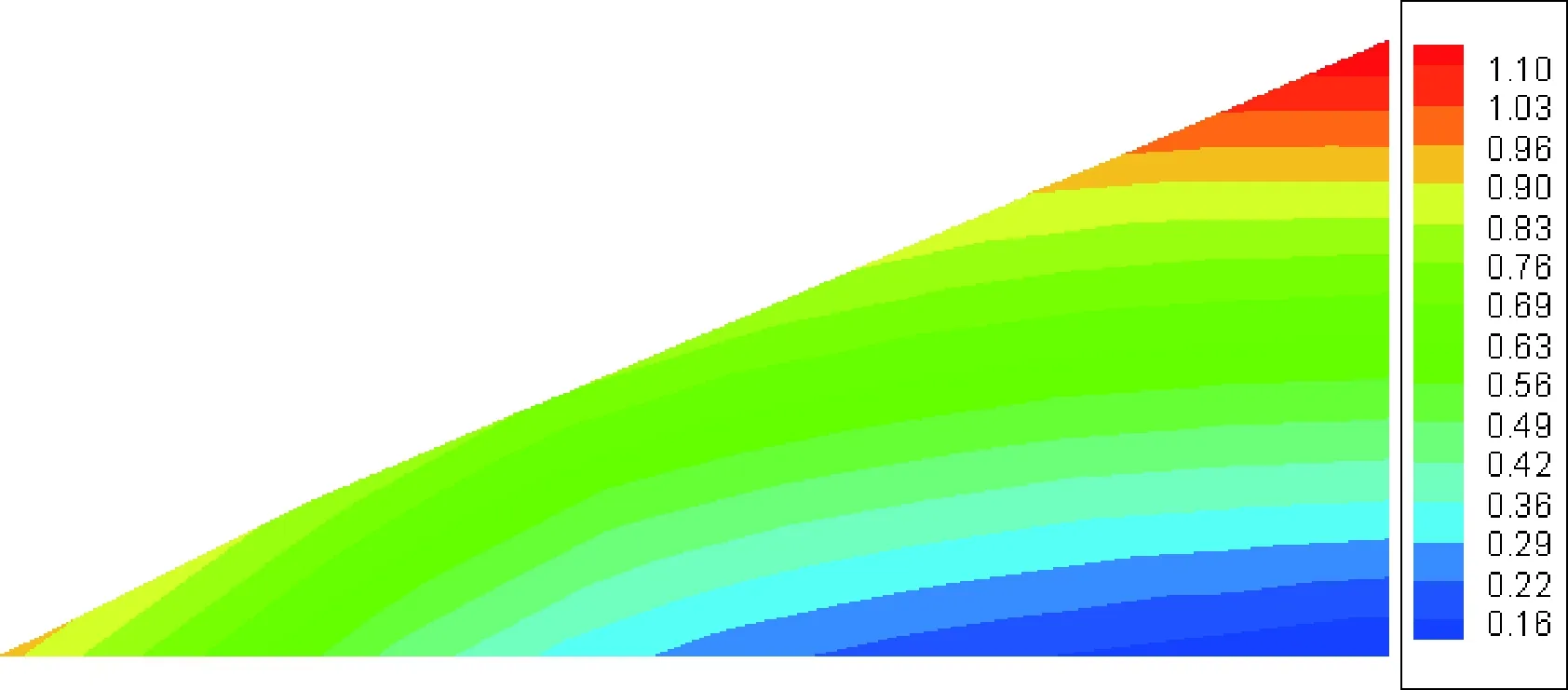
图7 有限元分析二阶振型图(弯曲)Fig.7 The second order bending mode by FEM

3 舵面颤振分析

颤振计算程序基于当地活塞流理论和小展弦比舵面颤振非定常气动力计算方法等编制而成，适用于舵及其它相近形式升力面超音速气动弹性问题的计算分析.该程序主要设计思想是用翼型表面的当地流速度VL代替无穷远处流速V∞作为参考速度，从而克服了经典活塞理论对翼型厚度和攻角的限制，可以在舵面模态参数确定的基础上，计算较大舵偏角和较大马赫数时的颤振临界动压和临界频率.

表2为舵面颤振临界参数计算结果，与模态试验工况对应分析了0°舵偏无载、0°舵偏有载(500 N)、15°舵偏无载和15°舵偏有载(500 N)共4种工况.由表2可知，舵偏角度和加载工况一定时，颤振临界动压随马赫数增大迅速增大，颤振临界频率随马赫数增大逐渐减小；舵偏角度一定时，有载工况颤振临界动压及临界频率均远高于无载工况；舵偏对颤振临界边界的影响随着马赫数增大而增大.

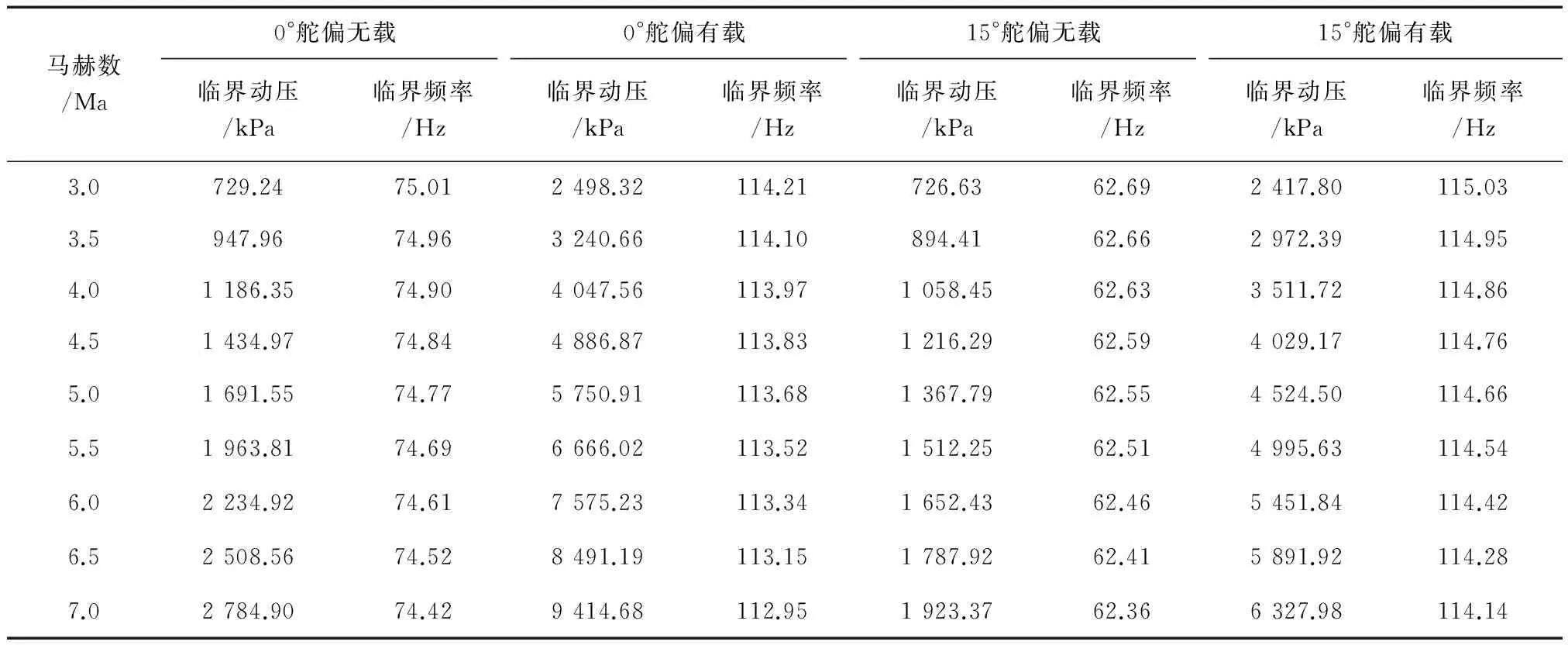
表2 颤振临界参数计算结果Tab.2 Flutter critical parameter results

图8为颤振临界动压示意图，可直观观察4种工况下临界边界对比情况.由图8可知：0°舵偏有载工况下颤振临界动压最高，不易发生颤振；15°舵偏无载工况下颤振临界动压最低，最易发生颤振.设计时保守考虑按15°舵偏无载工况确定颤振边界，低于该边界的区域为颤振安全区，其它区域为颤振危险区.

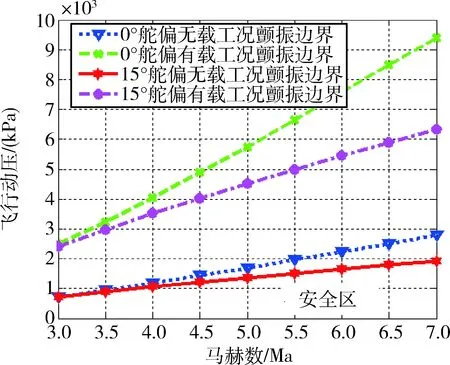
图8 颤振临界边界示意图Fig.8 Flutter critical boundary

4 结 论

(1)用当地活塞流理论可计算小展弦比有限厚度三角舵面非定常气动力，飞行参数确定后，在模态坐标下求解系统动力学方程特征根即可求得颤振临界动压和临界频率；

(2)舵偏角度和加载工况一定时，颤振临界动压随马赫数增大而增大，颤振临界频率随马赫数增大而减小；舵偏角度一定时，有载工况颤振临界边界高于无载工况；舵偏对颤振临界边界的影响随舵偏角度增大而增大；

(3)有舵偏无载工况颤振临界边界最低，是最易发生颤振的工况，保守考虑将此边界定为舵面颤振临界边界，低于该边界的区域为安全区，飞行参数在安全区内则不会发生颤振；

(4)舵面结构设计时应充分考虑颤振的影响，确保结构设计的安全性和合理性，为型号研制和飞行试验的成功提供保障.

参 考 文 献

[1] 陈桂彬,邹万青,杨超等.气动弹性设计基础[M].北京:北京航空航天大学出版社，2004：94-103.

[2] 张伟伟,樊则文,叶正寅.超音速、高超音速机翼的气动弹性计算方法[J],西北工业大学学报，2003,21(6):687-691.

ZHANG W W, FAN Z W， YE Z Y, et al. A better engineering method for computing aeroelastic characteristics of supersonic and hypersonic wings[J].Journal of Northwestern Polytechnical University, 2003,21(6): 687- 691.

[3] 吴俊,朱瑾.小展弦比翼面颤振分析方法研究[J].现代防御技术,2009,37(6):31-50.

WU J, ZHU J. Flutter analysis of low aspect ratio wing surface[J].Modern Defence Technology, 2009,37(6):31-50.

[4] 张仁嘉,吴志刚,杨超.电动伺服舵系统动力学建模及颤振分析[J].北京航空航天大学学报, 2016,42(7):1368-1376.

ZHANG R J, WU Z G, YANG C. Dynamic modeling and flutter analysis of a fin-actuator system[J].Journal of Beijing University of Aeronautics and Astronautics, 2016,42(7): 1368-376.

[5] 张永超,朱瑾,刘炜. 舵面热颤振分析研究[J].现代防御技术,2014,42(1):36-39.

ZHANG Y C, ZHU J, LIU W. Analysis on thermal flutter of rudder with aerodynamic heating[J].Modern Defence Technology, 2014,42(1):36-39.

[6] 荆志伟,吴志刚,杨超.带燃气舵的导弹舵面颤振分析方法[J].北京航空航天大学学报,2010,36(8)：991-995.

JING Z W, WU Z G, YANG C. rudder flutter analysis method of missile with jetvane[J].Journal of Beijing University of Aeronautics and Astronautics, 2010,36(8)：991-995.

[7] 董军,卢晓杨,侯良学.带舵面垂尾跨声速颤振计算研究[J].航空计算技术,2014,44(5):42-45.

DONG J, LU X Y, HOU L X. Study on transonic flutter calculation of a vertical tail with rudder[J].Aeronautical Computing Technique, 2014,44(5):42-45.

[8] 樊则文,刘晓宁,杨炳渊. 超声速飞行器气动伺服弹性稳定性分析[J].上海航天,2008(4):22-25.

FAN Z W, LIU X N, YANG B Y. Aeroservoelastic stability analysis of a supersonic aircraft[J].Aerospace Shanghai, 2008(4):22-25.

[9] 杨炳渊,宋伟力.用当地活塞流理论计算大攻角翼面超音速颤振[J].振动与冲击,1995(2):60-63.

YANG B Y, SONG W L. Supersonic flutter calculation of a wing with attack angle by local flow piston theary[J].Vibration and Shock, 1995(2):60-63.