数控凸轮轴高速磨削性能研究及其优化改进

范培珍 何其宝

摘要：凸轮轴数控加工方式易因联动磨削产生较大加速度，影響磨削伺服系统性能。针对此问题，构建数控凸轮轴高速磨削数学模型，分析凸轮轴工件磨削动力学机理，得出工件进给最大加速度，分析加速度超过限值时工件转速变化趋势，以此验证传统方法的不足。在此基础上，提出基于最小二乘多项式拟合的优化算法，实时优化分析凸轮轴加工过程中工件进给加速度变化。实验结果证明该优化算法能够较好的拟合原始样本数据，具有较小的控制误差。

关键词：凸轮轴；数控；高速磨削；优化

中图分类号：TG580.2文献标志码：A文章编号：2095-5383（2018）01-0011-03

随着装备制造业的发展，内燃发动机关键部件——凸轮轴的需求量与日俱增，而传统加工工艺使得凸轮轴性能较差。目前国内普遍采用的是数控磨削工艺，相较于国外，数控凸轮轴磨削工艺仍存在不小差距，因此，如何提升凸轮轴数控磨削加工质量与效率成为了凸轮轴加工的主要研究热点之一。本文根据几何动力学构建凸轮轴加工数学模型，得到数控凸轮轴高速磨削方程式，分析凸轮轴加工质量，得出工艺改进策略。

1 数控凸轮轴高速磨削数学模型

凸轮轴升程数据会在数控程序中生成X-C联动程序，该程序进行插补运算，提高凸轮轴加工质量。

设：1）等磨削深度升程；2）恒线速度加工方式；3）去除率均匀，以此建立数控凸轮轴高速磨削数学模型。根据砂轮进给位移与凸轮实际运动的关系（如图1所示）可以得到：

由此，根据式（1）～（13），通过数值拟合便可得到工件转速与凸轮转角之间的关系，如图2所示。

2 数控凸轮轴高速磨削动力学分析

在实际运动中，砂轮围绕主轴做旋转运动。其中，砂轮沿着X轴方向做横向循环往复进给运动，并与凸轮工件耦合联动，因此，根据动力学原理，定义vp、vs、vj，其中，vs、vj分别表示砂轮切线速度、砂轮切线运动与凸轮的切点速度。

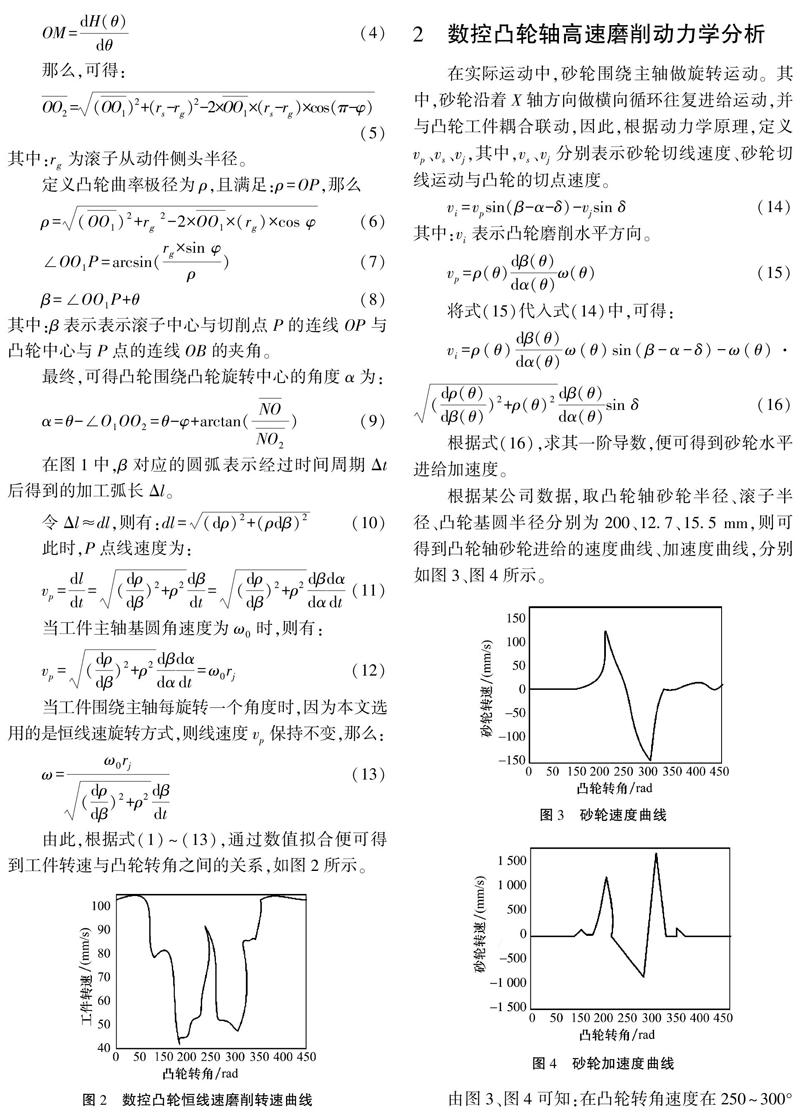
根据某公司数据，取凸轮轴砂轮半径、滚子半径、凸轮基圆半径分别为200、12.7、15.5 mm，则可得到凸轮轴砂轮进给的速度曲线、加速度曲线，分别如图3、图4所示。

由图3、图4可知：在凸轮转角速度在250～300°之间的时候，砂轮具有最大速度，约为150 mm/s；而此时可以获得最大加速度，约为1 500 mm/s2。

由图2～5可知，当凸轮转速约在150～300°之间的时候，工件磨削升程过程中出现了转速急剧上升继而急剧下降的趋势，使得砂轮加速度在此区域内出现时而急剧增大、时而急剧减小的变化趋势，这必将造成工件磨削出现不均匀的情况，因此，数控凸轮轴多通过改变C轴转速或者是改变砂轮进给加速度降低砂轮惯性冲击对工件加工质量的影响。

3 数控凸轮轴磨削转速优化

据统计，不同工件转速对凸轮轴高速磨削性能有着不同影响，尤其是加工凸轮非圆轮廓端时，砂轮接触工件表面的速度时刻变化，材料去除率存在较为严重的不均衡性。而传统凸轮工件转速优化方法均未考虑砂轮的速度、加速度是否超过系统允许限值，因此，直接计算凸轮工件转速，继而判断砂轮最大加速度是否超过系统允许限值的方法过去简单直接。

不同测点采集数据通过数据拟合便可获知凸轮轴加工升程数据是否光滑，继而判定凸轮轴轮廓线光滑度。因此，本文选用最小二乘多项式算法对数控凸轮轴磨削转速进行优化设计，其基本流程如图5所示。最小二乘多项式算法的核心思想是通过引入近似函数，构建基于凸轮轴轮廓值的最小误差平方和函数，保证数据点逼近误差的绝对值的平方和最小，从而滤除噪声信号。

取：1）某企业参数：滚子半径、凸轮基圆半径、最大升程分别为12.7、15.5、5.152 5 mm。2）凸轮升程样本数据。

根据最小二乘多项式拟合函数，可以得到拟合后的多项式函数：

其拟合曲线如图6所示。由图6可见，升程拟合值误差范围可以控制在0.002 mm，这预示着最小二乘多项式拟合算法对于凸轮转速有着比较好的预测优化性能。

4 结语

本文构建了数控凸轮轴高速磨削性能分析的数学模型，在此模型的基础上，从动力学原理出发，深入分析了凸轮主轴转速、砂轮转速之间的数学关系，证明了传统分析方法无法解决砂轮加速度急剧变化趋势。进而采取最小二乘多项式拟合算法对凸轮升程与转角的关系进行拟合，将原混杂有无效信号的凸轮轴信号拟合为有效的凸轮升程信号。实例分析表明此方法具有较小的误差控制。

参考文献：

[1]曹海印， 张艳明， 闫圣达，等. 高速凸轮轴磨床砂轮电主轴的有限元分析[J]. 机械制造， 2017， 55（8）：40-42.

[2]杨寿智， 邓朝晖， 吴桂云，等. 凸轮轴数控磨削工件主轴转速优化建模与实验研究[J]. 中国机械工程， 2016， 27（5）：652-657.

[3]余良伟， 陈绪兵， 余志，等. 凸轮轴磨削加工升程误差测量及抑制方法分析[J]. 工具技术， 2016， 50（8）：104-106.

[4]范晋伟， 王鸿亮， 张兰清，等. 数控凸轮轴磨床运动误差分析与建模技术[J]. 北京工业大学学报， 2017， 43（2）：203-209.

[5]范晋伟， 王鸿亮， 唐宇航. 数控凸轮轴磨床误差建模与辨识技术理论研究[J]. 振动与冲击， 2017（18）：257-264.

[6]张晓红， 邓朝晖， 万林林，等. 多方法集成的凸轮轴磨削工艺智能优选研究[J]. 现代制造工程， 2016（12）：31-36.

[7]谢智明， 邓朝晖， 刘伟，等. 凸轮轴数控磨削云平台的研究与设计[J]. 中国机械工程， 2016， 27（1）：91-100.

[8]邓朝晖， 皮舟， 黄琦，等. 凸轮轴高速数控磨床主轴静动态特性[J]. 湖南科技大学学报（自然科学版）， 2015， 30（4）：27-33.