测量不确定度估算在职业卫生检测中的应用
田晓朋 韩余
【摘要】不确定分析法计算圈闭资源量可为项目潜力评估快速提供参考,较确定性算法更为客观,认识更为全面。较建模法,对原始性数据依赖性相对较小,更易实现,是勘探类新项目评价的有效手段。鉴于此,本文主要分析测量不确定度估算在职业卫生检测中的应用。
【关键词】职业卫生检测;测量不确定度估算;应用
一、概述
美国核管会(NRC)最初法规要求核电厂设计或安全分析中应用过度保守的模型或假设以确保足够的安全裕度,然而,核设施安全委员会(CSNI)的研究表明保守模型或假设偏离真实情况较大,并不一定产生保守结果。1988年,美国NRC对联邦法规10CFR50.46进行了补充,允许应用最佳估算方法作为保守模型方法的替代方法,但最佳估算结果必须进行不确定度评估,以足够高的概率证明燃料包壳峰值温度、局部最大氧化份额等不会超过设计准则。最佳估算+不确定度(BEPU)方法最初主要应用于大破口失水事故(LOCA)分析,后来逐步成为核电厂安全分析的一种趋势。近年来,多种BEPU方法已获得核监管当局(如美国NRC)的评审认可,部分已用于核电厂最终安全分析报告的评审中,并逐步在小破口LOCA、核电厂功率提升、重新取证或新设计认证等方面应用。
该项目主要由两大部分组成:一是针对LOFT台架L2—5试验开展相关热工水力最佳估算程序的不确定度评估和敏感性分析;二是对核电厂进行最佳估算+不确定度评估和敏感性分析。项目指出了不确定度评估中的一些关键问题。
二、参数相关性分析
资源评价中地质参数之间的相关性是一个不容忽视的因素,可以确保随机取样符合地质条件的约束。如不考虑,必然会影响资源估算结果的合理性。每个参数都反映了油气资源富集的信息,这些信息彼此之间存在一定的相关性,参数及其相关性共同反映地质总体特征。
如果一个参数随着另外一个参数的增大(减小)而增大(减小),则这2个参数满足正相关关系;反之,则这2个参数满足负相关关系。相关系数取值范围从—1到1。—1表示最大负相关,1表示最大正相关。取值为0,则表示没有相关性。在实际应用时,对于具有实际井上数据的2个参数,可以利用散点统计法呈现彼此相关性,并量化为相关系数,如孔隙度与含水饱和度、有效厚度与孔隙度等。对于难以统计但理论上存在相关性的参数,则需要根据油气藏具体地质情况结合经验判断确定相关系数,以避免概率模拟出现异常值。
三、测量不确定度估算在职业卫生检测中的应用
(一)A类不确定度的估算
在实际的测量中,并不能进行无限次的测量,因此测量误差很多情况下并不会符合正态分布,在这种情况下就需要乘以一个因子,A类不确定度分量一般是指随机误差,依照误差理论,重复次数足够多的情况下,能够得到不确定度分量。A类不确定度的估算方法包括赛贝尔法、合成样本标准差、极差法等。最基本的方法是经过重复性和复杂性的试验观察,得到可靠性的参数,计算标准不确定度。
很多测验是在不同实验室中完成,同时由于测量人员的不同也会造成误差,因此会得到多组分测量结果,在测量不确定度时,以几个数据为一组,测量一个均值,得到不确定度。
(二)2B类不确定度的估算
B类不确定度来源很多都是现成的,这类评定在理化检验中很少使用,主要包括以前的测量数据、仪器的误差以及准确度的级别等。依照我国相关标准,同时被测量xi包括不确定U(xi)及置信概率p,则标准不确定度U(xi)=U(xi)/kp,在已知信息标准xi之值分散区间a的情况下,标准不确定度U(xi)=a/k,k值大小与分布有关,见下表所示,图形分布的包含因子与β值有关。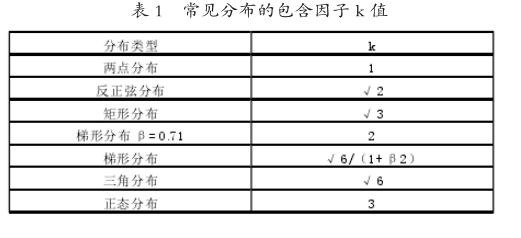
四、測量不确定度估算在职业卫生检测中应用应注意的问题
针对工作场所中的危险因素,通过不确定度的评定来分析来源,评定现有实验室检查方法,提高准确度,进而得到更加权威的报告,在分析测量不确定度在职业卫生检测中的应用中主要分析粉尘和造成不在确定度分析。在职业卫生报告测量结果时,需要同时分析测量结果的质量,若是没有这种表示,无法比较测量结果。在职业卫生工作大量检测项目中,粉尘和噪声是最常见的检测项目,是质量控制的关键环节,粉尘的不确定度主要由采样仪器引起,在以后的职业卫生检测中需要注意,购买误差小的设备,减小测量不确定度。在具体的测量中很多系统误差难以矫正和发现,因此在测量中还需要核对标准物质和系统误差提高测量结果的准确性。
总之,本文主要分析测量不确定度在职业卫生检测中的应用,在职业卫生监测分析评估不确定度中,需要注意分析不确定度的来源,及时发现并控制影响因素,加强质量控制,提高检测结果准确度。
参考文献
[1]高建丽.冲击加速度测量不确定度的评估方法研究[D].太原:中北大学,2017.
[2]贾翠红,赖恒,雷晋萍.测量不确定度及其估算[J].福建师范大学学报(自然科学版),2007(01):96~99.
[3]卢济深.测量不确定度在不同过程中的估算[J].工业计量,2005(02):44~46.
[4]李慎安.测量不确定度估算程序图[J].计量技术,1999(11):43~45.

