BTO环境下的汽车供应链实时排程研究

冯晓川 李江洁

摘 要：针对BTO环境下汽车供应链的敏捷性、精益性需求，提出基于延迟策略、模块化制造的实时排程模型与算法，该模型将一般装配过程分解为简单装配过程，基于简单装配排程的线性搜索算法，迭代生成一般装配过程的排程。再通过设备排程状态与订单工序需求等实时数据进行仿真，仿真结果表明该排程模型及实时算法可以缩短总装提前期，并能保持系统对定制部分操作时间波动的稳定性.此排程模型与算法具有较好的效率，能用于询单、调度和协同等的实时决策支持。

关键词： BTO;实时供应链;汽车行业;总装排程;实时算法

中图分类号： TH 166文献标志码：A文章编号：1006-8023（2018）06-0067-04

Research on Real-time Scheduling of Automotive Supply Chain under Builder-to-order

FENG Xiaochuan， LI Jiangjie

（Department of Information， Beijing City University， Beijing 100086）

Abstract：This paper proposes a real-time scheduling model and algorithm based on the delayed different strategy and modularity oriented to the agility and lean character of automotive supply chain. We decomposed general assembly process into ordinary assembly process， and modeled real-time assembly scheduling and proposed the algorithm flow based on the linear search algorithm of ordinary assembly process. The simulation result with real-time data of device scheduling state and order demand shows that the real-time scheduling model can short the dynamic general assembly lead time and keep the stability for operation time fluctuation of customized components， and the algorithm is so efficient that it can support real-time decision in order quotation， dispatch and coordination.

Keywords：BTO; real-time supply chain; automotive industry; general assembly scheduling; real-time algorithm

0 引言

面向订单生产BTO（Build-to-order）的制造模式不限于通过零部件的组合配置来满足客户的个性化需求，对部分零修改部件按订单生产而大部分基于库存组合来实现，介于ATO与MTO之间，英国的3DayCar及欧盟的ILIPT研究项目都指出BTO是未来汽车生产的主要模式。总装及MTO部分零部件的生产对订单的按时交付至关重要，相应的排程对在制品库存WIP、资源利用及订单变更的响应都具有较大影响[2] 。供应链排程方法很多，比如模糊排程[4]、实时排程[3]及执行过程中对不确定性的响应问题[5-6]。模糊排程基于智能算法考虑了过多的因素，其算法的效率和实时性不足为：现有的实时排程算法则将树状的装配过程线性化分解，同一作业出现在多个线性过程，产生同步约束，这样的处理增加了问题的复杂度。本文通过延迟策略和模块化制造将总装过程分成MTS与MTO两段，个性化需求部分靠近装配后段，复杂的总装过程可以作较大程度的简化;MTO零部件供应商与总装企业紧密集成，RFID、移动互联网等实时技术的发展，都为MTO零部件供应商与总装企业间订单变更、供应链执行的实时信息共享提供了条件。本文研究BTO环境下的实时排程方法，着重研究总装过程的分解、模型建立与实时算法。

1 装配过程分解

一般的装配过程在Z个工序完成，用集合表示为{ A1，A2，…，AZ }，每一个工序AZ需要装配lZ （lZ≥2）个零部件（序号用j表示），每一个零部件在工序z的装配可以分解为一系列的操作，表示为u = 1，2，…，Mj，Z;j = 1，2，…，lZ;  z = 1，2，…，Z。每一个最小的加工装配过程可以用一个三元关系表示为（u，j，z），记为i，一般的装配过程如图1所示。图1中有填充的方框表示物流过程，物流资源扩充容易，这类过程受资源约束小;只有一个前驱的过程表示简单加工过程，有多个前驱的过程表示装配过程，没有前驱的表示从仓库领货及定制件的采购或加工过程。

操作u可以在Ku台设备上完成，表示为，每台设備的空闲时间段（可用时间窗口）用区间集合表示为。所有设备可用时间窗口按以下规则排序：对于任意的k1≠k2，并用k1，k2∈{1，2，…，ku}，时间窗口在下列情况下排在时间窗口的前面。

，或者并且基于以上的排序原则，对所有Ku台设备的可用时间窗口进行排序，得到操作u可以排程的时间窗口序列，表示为，每个时间窗口的上标对应着相应的设备编号。

一般的装配过程排程比较复杂，可以将其中的部装看成一个整体，每个装配操作的前驱就是简单的线性操作过程，排程得到部装的开工时间后，用同样的方法对部装的前驱进行排程，迭代完成整个排程工作。简化过程可以从装配的最后一道工序开始，使所有装配的所有前驱都成为线性过程。如果某个节点有多个前驱，则该线性过程分解停止，进行其它前驱过程的搜索;将有多个前驱的节点进行类似的分解，让所有的过程都只有最后一个节点有多个前驱，其所有前驱为线性过程。图1的一般装配过程，可以分解为图2的简单装配过程。

2 模型建立

用t（u，j，z）表示操作（u，j，z）的开工时间，用θ（u，j，z）表示该操作的标准工时，δ（u，j，z）表示该操作完成时间波动上限，即完成操作的最大时间为θ（u，j，z）+δ（u，j，z）。

排程的目标是在交货期约束下，使装配工序特别是定制部分的开工时间最晚，以让订单修改等需求不确定性的影响最小化。目标函数和约束条件表示为：

J = max（t（ul，jl，z+l）+θ（ul，jl，z+l）） 。       （1）

s.t.：

u（u，j，z）∈ [θ（u，j，z），θ（u，j，z） + δ（u，j，z）]，（u，j，z）。 （2）

t（u，j，z）+ u（u，j，z）≤ t（ul，jl，zl） 。         （3）

（u1，j1，z1）是（u，j，z）的后继操作。

J < delivery time 。                        （4）

公式（1）目标函数表示当前装配工序最晚完工时间;公式（2）表示工时约束，实际工时在标准工时上有一个最大偏差;公式（3）表示前驱后继约束;公式（4）表示完工时间必须早于交货期。

3 实时算法

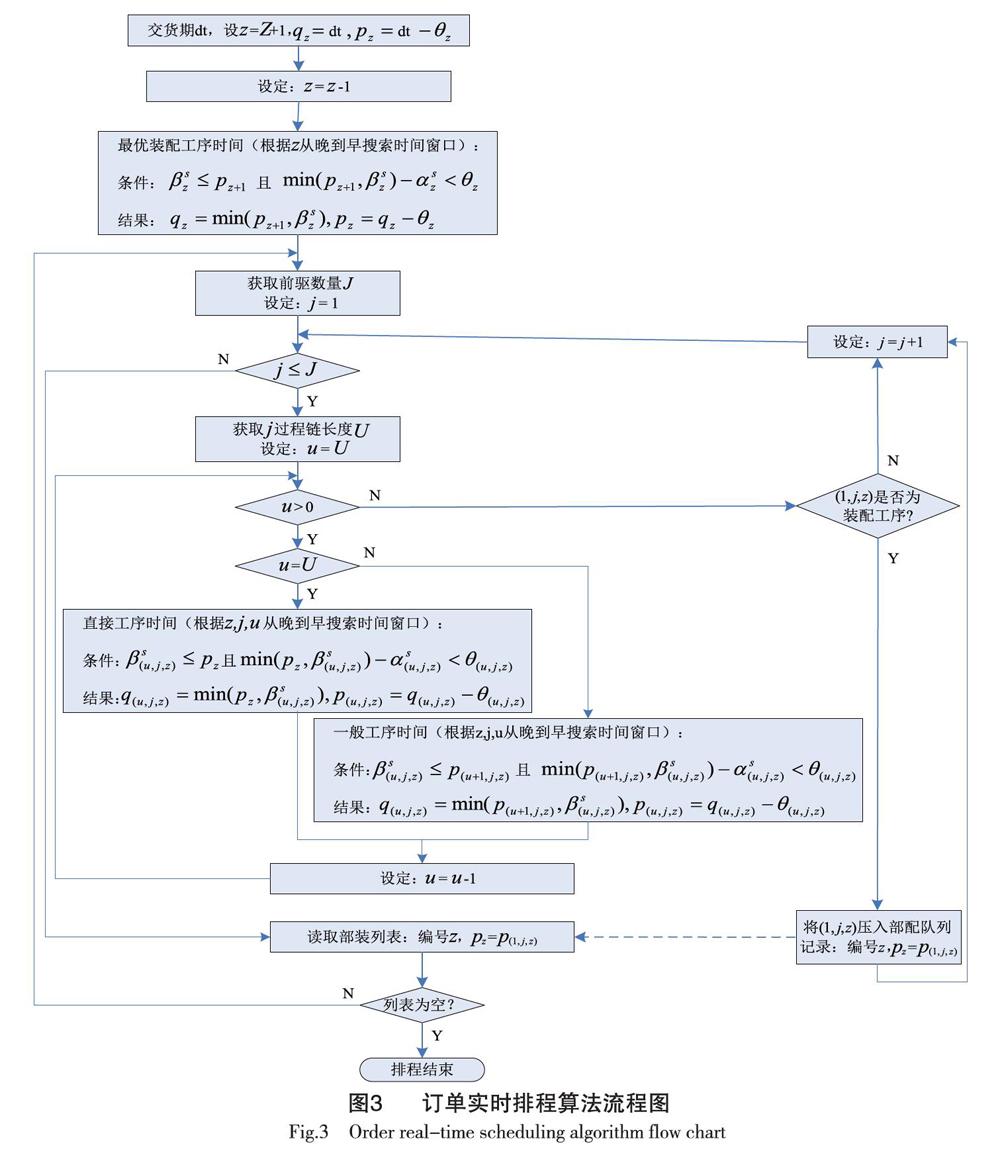
排程除满足上一节的目标外，算法实时性要求对交货期询单和执行过程的调度也具有重要意义。实时排程可分为3个步骤：①一般装配过程的分解;②简单装配排程;③总装排程由简单装配排程迭代产生。一般装配过程到简单装配过程的分解见前面介绍，简单装配排程由线性分支组成，只有一个装配操作即根节点，倒排搜索即可完成，迭代形成总装排程的算法流程如图3所示。

图3中p表示各工序开工时间，q表示各工序完工时间，其它参数同前面所述。首先根据订单交货期计算最后一道装配工序的开工时间，然后计算各前驱过程链的排程，对每一过程链，由后往前根据工序时间和资源时间窗口确定最晚开工时间。如果某一过程链中存在装配节点，将该节点的开工时间视为简单装配节点，重复上述过程，迭代完成订单排程计算。

4 实例分析

汽车装配过程复杂，但BTO环境下基于延迟策略与模块化思想，将定制部件和与之相应的装配，通过供应链设计将其配置在总装的后期完成，将标准部分的装配及流水线操作部分简化为整体，以降低计算的复杂度。本文假设将这一过程简化为图1，依据总装工序搜集相应设备及其在某订单交货期前后的排产情况，采用基于图3流程开发的算法进行仿真计算，可以得到图4中填充模块的仿真排程结果。图1总装过程各工序的标准工时及其波动见表1，工序所依賴设备的已有排程情况如图4所示，矩形方框表示设备的空闲即可用时间，不同高度代表不同的设备。仿真排程结果在图4中表示为实填充，排程操作所依赖的设备用斜线填充方框代表的设备编号决定。

5结束语

本文将实时算法用于BTO环境下的总装排程问题，对每个操作，每一设备有多个可用的时间窗口，同类设备的可用时间窗口形成更大的集合，可以进行统一的排序。在执行过程中，每个操作实际完成时间会在θ（u，j，z）与θ（u，j，z）+ δ（u，j，z）间形成微小的时间窗，需要对未执行的操作进行调整，以提高资源利用率。

实时排程针对订单进行，各操作可视为原子操作，不需拆解，搜索加工设备的可用时间窗口较快。因此，可用于BTO环境下对个性化需要部分的操作进行定制，实时总装排程也可用于辅助询单过程以及执行过程中调度与协同的排程重算。

【参 考 文 献】

[1]GUNASEKARAN A， NGAI E.W.T. Build-to-order supply chain management： A literature review and framework for development[J]. Journal of Operations Management， 2011，23（5）： 423-451.

[2]PARRY G， GRAVESA. Build to order： the road to the 5-day car[M].London： Springer-Verlag， 2008.

[3]PROTH JM. Scheduling： new trends in industrial environment[J].Annual Reviews in Control， 2007，31（1）： 157-166.

[4]DEMIRLI K， YIMER A D. Fuzzy scheduling of a build-to-order supply chain[J]. International Journal of Production Research， 2008，46（14）：3931-3958.

[5]KRAJEWSKI L， WEI J C， TANG L L.Responding to schedule changes in build-to-order supply chains[J].Journal of Operations Management， 2005，23（5）：452-469.

[6]AYTUG H， LAWLEY M A， MCKAY K. Executing production schedules in the face of uncertainties：A review and some future directions[J]. European Journal of Operational Research， 2005， 161（1）：86-110.

[7]FALISZEWSKI P， HEMASPAANDRA E， HEMASPAANDRA L A. The complexity of manipulative attacks in nearly single-peaked electorates[J]. Artificial Intelligence， 2014， 207： 69-99.

[8]ERDELYI G， LACKNER M， PFANDLER A. Computational aspects of nearly single-peaked electorates[C]. Proceedings of the 27th AAAI Conference on Artificial Intelligence （AAAI-13）， Bellevue， USA， 2013：283-289.

[9]CORMAZ D， GALAND L， SPANJAARD O. Kemenyelections with bounded single-peaked or single-crossing width[C]. Proceedings of the 23rd International Joint Conference on Artificial Intelligence （IJCAI-13）， Beijing， 2013：76-82.

[10]MOULIN H. On strategy-proofness and single-peakedness[J]. Public Choice， 1980， 35（4）：437-455.

[11]MASSO J，BARREDA I M D. On strategy-proofness and symmetric single-peakedness[J]. Games and Economic Behavior， 2011， 72（2）：467-484.

[12]BORDER K C， JORDAN J S. Straightforward elections， unanimity and phantom voters[J]. Review of Economic Studies， 1983， 50（1）：153-170.

[13]LU P Y， SUN X R， WANG Y J， et al. Asymptotically optimal strategy-proof mechanisms for two-facility games[J]. Electronic Commerce， 2010： 315-324.

[14]FOKAKIS D， TZAMOS C. Winner-imposing strategy-proof mechanisms for multiple facility location games[C]. Proceedings of the Sixth International Workshop on Internet and Network Economics （WINE-10）， Stanford， USA， 2010：234-245.

[15] 智川，李志健，冷彩鳳.色度空间转换模型评价体系的研究[J].陕西科技大学报， 2013，31（4）：20-23.

ZHI C， LI Z J，LENG C F. Study on evaluation system of color space conversion methods[J]. Journal of Shanxi University of Science & Technology， 2013，31（4）：20-23.

[16] FOKAKIS D， TZAMOS C. On the power of deterministic mechanisms for facility location games[C]. International Colloquium on Automate， Languages， and Programming， 2013： 449-460.

[17]LU P Y， WANG Y J， ZHOU Y. Tighter bounds for facility games[C]. Proceedings of the Fifth International Workshop on Internet and Network Economics （WINE-09）， Rome， Italy， 2009： 137-148.