基于卡尔曼滤波算法的姿态仪设计
蒲晓湘1,周世纪
(1.重庆电力高等专科学校,重庆 400053;2.重庆大学 电气工程学院,重庆 400044)
姿态仪主要用于飞机、导弹和火箭系统等飞行器航行参数的监控,如几何角度测量、速度、加速度等惯性量的测量,也广泛应用于航模无人机、机器人、人体运动分析等需要低成本、高动态三维姿态测量的产品设备中。
本文在传统姿态仪基础上,引入了卡尔曼滤波算法,设计了一种新型航姿系统,大大提高了测量和控制精度。它可实时提供载体运动的姿态角(航向、俯仰角和滚动角)、角速率、加速度等信息,其还具有体积小、质量轻、抗冲击振动、性价比高和供电方便等特点,可满足航空、航天车载等的测量及控制要求。该姿态仪在标准转台上进行了测试,并用MATLAB仿真验证了本文所用算法的正确性和有效性。
1 硬件设计及分析
1.1 硬件组成
如图1所示,航姿仪的硬件部分由惯性测量单元(IMU)、输入接口、输出接口、导航计算机和二次电源等部分组成。
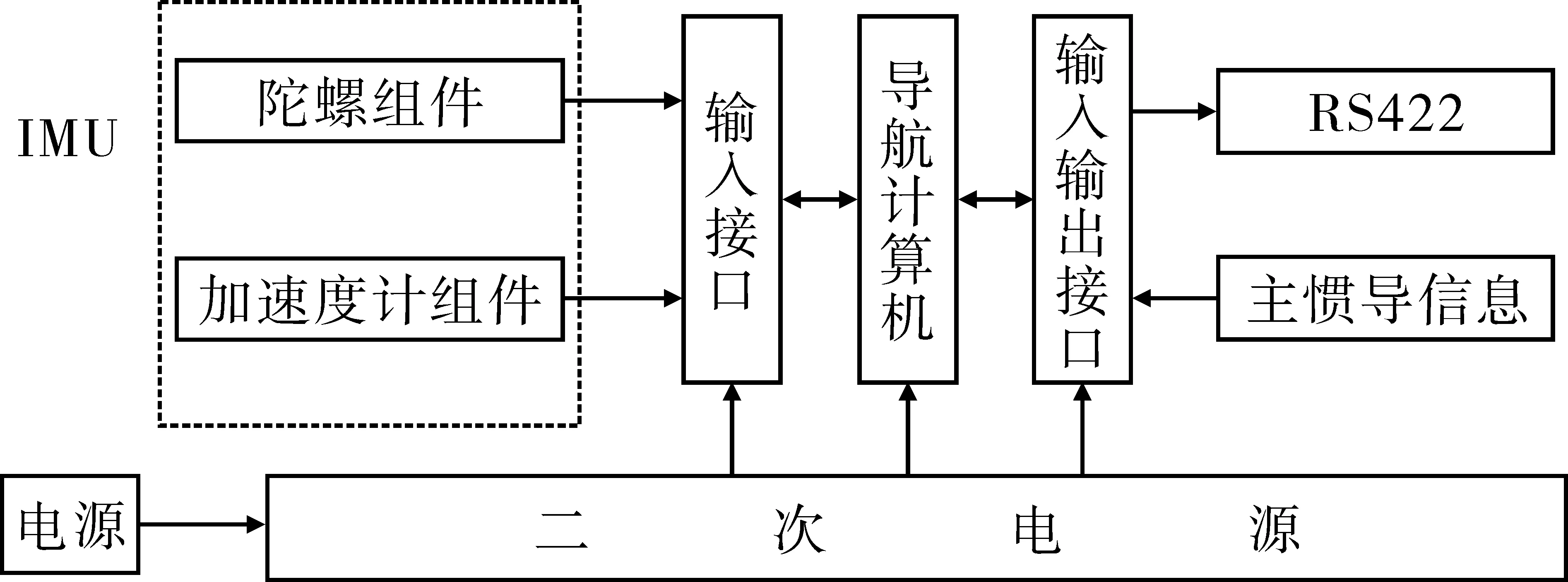
图1 航姿仪的硬件组成框图
1.2 IMU选择
1.2.1 加速度计的设计
动态姿态组合仪技术指标中,姿态精度要求小于0.1°。因此,根据系统姿态初始对准原理,可得到加速度计的精度估算公式。
(1)
式中:δθ为初始姿态误差;Δ为加速度计误差;g为重力加速度。根据式(1)可得到系统对加速度计的精度要求为
Δ<1.72 mg
(2)
对误差进行软件补偿,可以使加速度的精度达到1 mg,满足系统对加速度计的精度要求。
1.2.2 陀螺仪的设计
姿态更新算法中,陀螺仪的测量精度直接影响系统的姿态精度。加速度计的精度若达到1 mg,可估算出姿态初始对准误差为
(3)
由于系统对姿态精度要求为0.1°,可以估算出陀螺的精度要求为
δθ=εt<0.04°
(4)
式中:ε为陀螺仪的精度;t为卡尔曼滤波修正周期。该动态姿态组合仪中,卡尔曼滤波周期为0.05 s,考虑到修正后的误差,初步要求陀螺的精度为
ε<0.08°/s
(5)
1.3 导航计算机的选择
姿态仪更新算法和各种滤波算法都由导航计算机完成。导航计算机是制导装置的中心控制器,它控制A/D转换、摄取数据,以及进行数据预处理和姿态计算。它的工作量相当繁重,且工作周期短,要在一个周期内完成各项控制任务,并进行十分复杂的卡尔曼滤波解算,这就要求计算机运行速度快。根据这些要求,仅单独使用现有的单片机和DSP难以满足上述复杂的控制和运算,实验证明,在此情况下采用基于DSP和C8051单片机的主从式双CPU导航计算机可以胜任该项工作。
1.4 输入/输出接口
输入接口主要是将IMU输出的原始信息转换成数字信号和外部的辅助信息送入导航计算机,输出接口主要是将导航计算机计算出的导航信息传送给上位机,此接口按技术协议采用RS422方式与上位机通信,具体通信协议按用户要求进行。
加速度计和陀螺的信号要输入到导航计算机,就需要把模拟量转换为数字量,考虑系统对信号转换的精度要求较高,本文选用了16位高速A/D转换器。
2 导航解算原理基本原理
姿态仪的IMU部分由3个速率陀螺和3个加速度计组成。陀螺测得的载体角速度信息和加速度计测得的载体加速度信息由数据采集器进行模/数转换后被送入导航计算机。导航计算机对采样数据进行预处理,且利用这些数据进行载体姿态更新,然后通过融合机载主惯导信息不断修正纯惯导时间累积的误差,满足长时间高精度测量需要,制导解算原理及过程如图2所示。
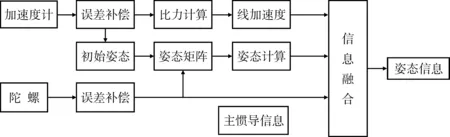
图2 导航解算原理框图
3 软件设计及分析
3.1 陀螺误差补偿
姿态仪的软件采用模块化设计,包括输入模块、输出模块、误差补偿模块、姿态更新计算模块和初始对准模块。最核心的就是误差补偿模块、姿态更新计算模块,本文主要对误差补偿模块作详细阐述。
误差补偿模块输入主要来自陀螺信号和加速度信号。
对陀螺的误差补偿主要分为两大部分:陀螺信号的初始补偿和卡尔曼滤波动态补偿。其补偿原理如图3所示。

陀螺信号的初始补偿主要补偿陀螺的零位误差、比例系数和安装误差引起的交叉耦合。其补偿的数学模型为
(6)
陀螺信号的动态补偿,主要是通过卡尔曼滤波技术对陀螺的漂移进行实时的估计,并且实时地进行补偿。在卡尔曼滤波中,建立的陀螺的误差模型为
ε=εc+εg+εr
(7)
式中:εc为随机常值漂移;εg为随机白噪声漂移;εr为随机一阶马尔柯夫过程漂移。
3.2 加速度计误差补偿
对加速度计的误差补偿同样分为两大部分:加速度计信号的初始补偿和卡尔曼滤波动态补偿。其补偿原理如图4所示。

加速度计信号的初始补偿主要补偿加速度计的零位误差、比例系数和安装误差引起的交叉耦合。其补偿的数学模型为
(8)

加速度计信号的动态补偿,主要是通过卡尔曼滤波技术对加速度计的漂移进行实时的估计,并且实时地进行补偿。与陀螺的模型不同,在卡尔曼滤波中,加速度计误差认为由两部分组成,随机白噪声误差和随机一阶马尔柯夫过程误差。
(9)
3.3 卡尔曼滤波算法
首先,根据位置误差方程、速度误差方程、姿态误差方程和陀螺、加速度计的随机误差方程,建立系统的状态方程为
(10)
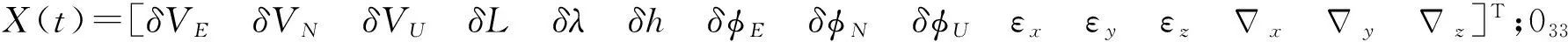
在深入分析和研究该数学模型的基础上,建立离散的卡尔曼滤波系统模型为
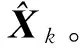
状态一步预测方程为
状态估计方程为
滤波增益方程为
Kk+1=Pk+1/kHTk+1(Hk+1Pk+1/kHTk+1+Rk+1)-1
一步预测均方误差方程为
估计均方误差方程为
Pk+1=(I-Kk+1Hk+1)Pk+1/k
4 系统仿真
在标准测试台上,利用MATLAB软件对本文设计的姿态仪进行仿真。
水平零位位置时,x,y,z轴姿态数据如图5~7所示。从图中可以看出,在零位位置时,3个轴向数据性能指标都能达到0.1°以内,满足要求。
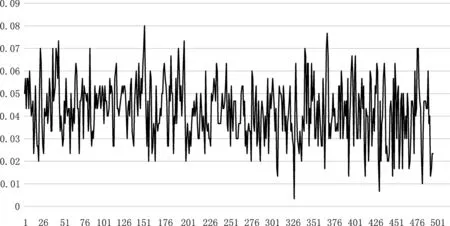
图5 水平零位位置时,x轴姿态数据
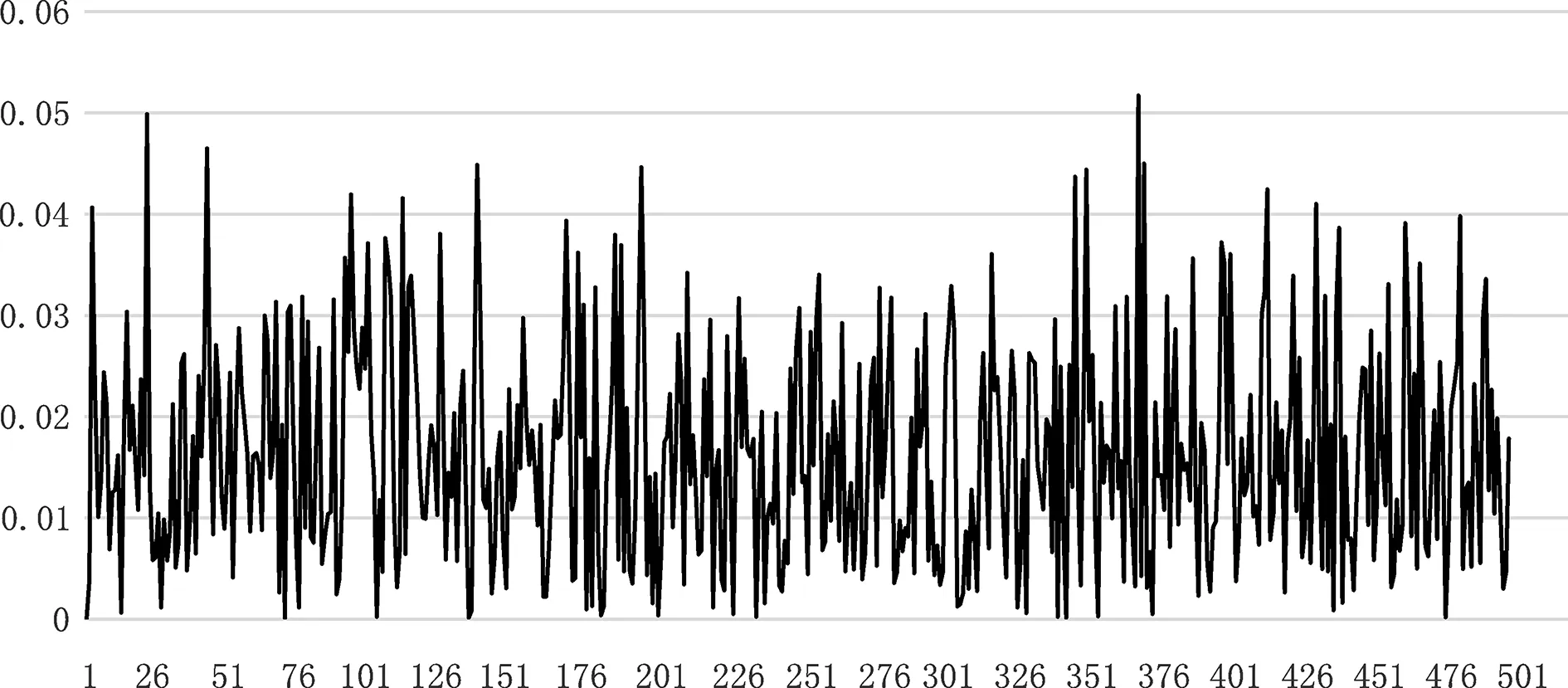
图6 水平零位位置时,y轴姿态数据
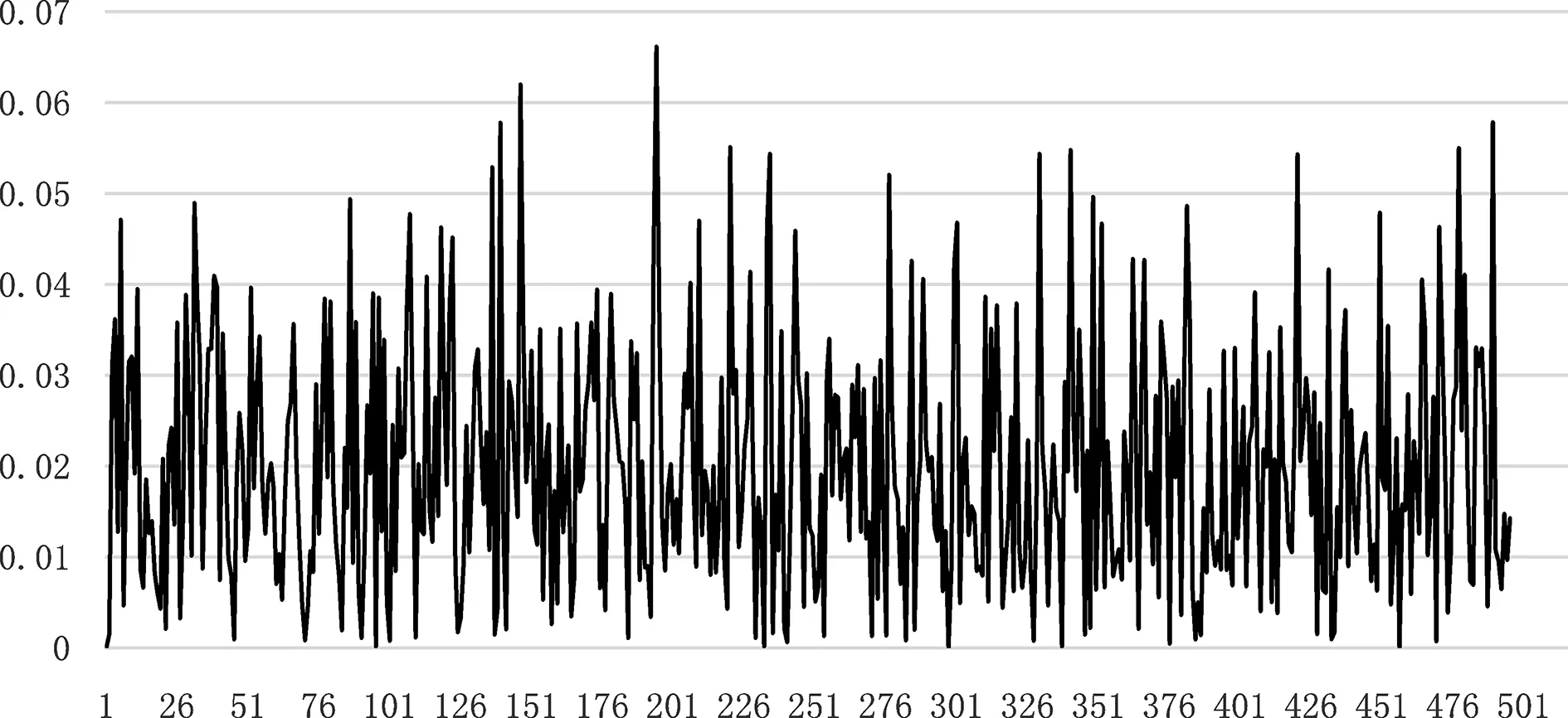
图7 水平零位位置时,z轴姿态数据
x,y,z轴倾斜15°时,姿态数据如图8~10所示。从图中可以看出,通电后,姿态数据经过短暂的震荡后收敛在-15°附近,精度稳定在0.1°以内,符合设计要求。
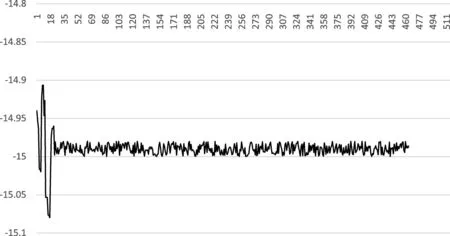
图8 x轴倾斜15°时姿态数据
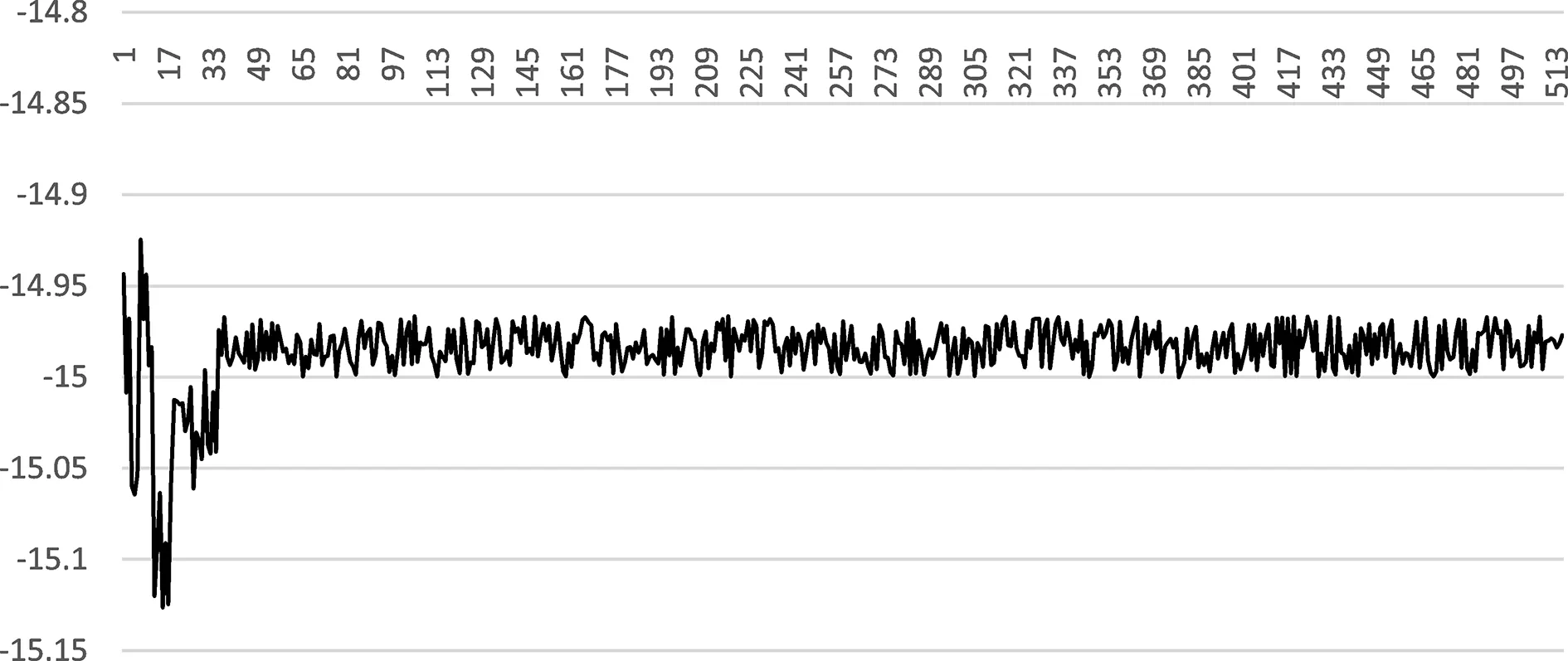
图9 y轴倾斜15°时姿态数据
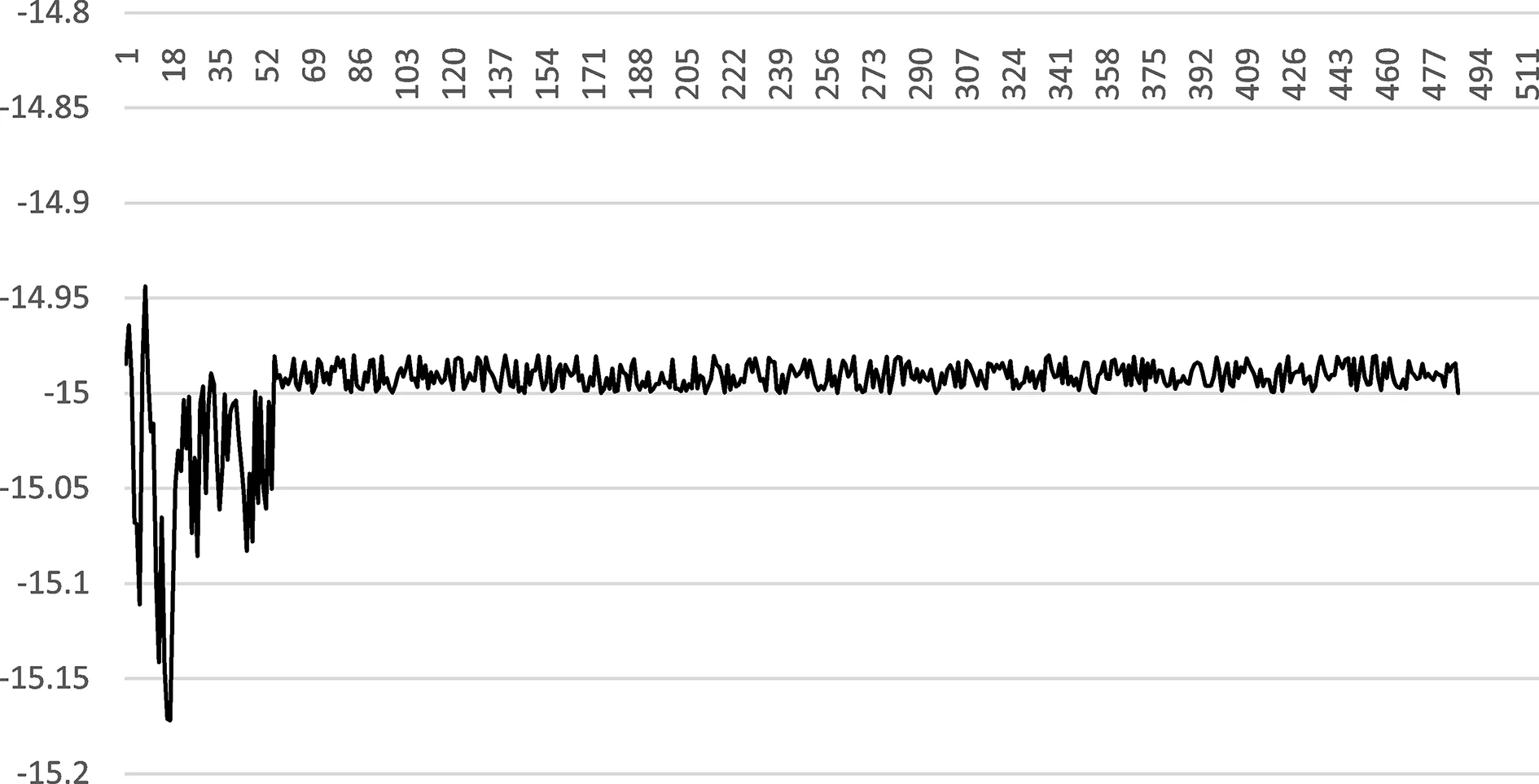
图10 z轴倾斜-15°时姿态数据
5 结语
相对于传统的航姿仪,本文设计姿态仪,在软件部分的误差补偿模块中引入卡尔曼滤波,对误差进行实时补偿,控制运算精度高,更好地满足测量及控制要求。该系统硬件部分在标准转台上进行了测试,对本文所采用的算法,利用MATLAB仿真软件,验证了算法的正确性和有效性。
参考文献:
[1] CUYPERS W,VAN GESTELB N,VOET A,et a1. Optical measurement techniques for mobile an d large scale Dimensional metrology [J].Optics and Lasers in Engineering,2009,47(3-4):292-300.
[2] 高青,袁亮,吴金强.基于新型LQR的四旋翼无人机姿态控制人机姿态控制[J].制造业自动化,2014(10):13-16.
[3] 秦勇,臧希酷,王晓宇,等.基于MEMS惯性传感器的机器人姿态检测系统的研究[J].传感技术学报,2007,20(2):298-301.
[4] 秦永元.惯性导航[M].北京:科学出版社,2006:297.
[5] 刘兴川,张盛,李丽哲,等.基于四元数的MARG传感器姿态测量算法[J].清华大学学报(自然科学版),2012,52(5):627-631.
[6] SUH Y S.Orientation estimation using a quaternion-based indirect Kalman filter with adaptive estimation of external acceleration[J].IEEE Transactions on Instrumentation and Measurement,2010,59(12):3 296-3 305.
[7] 徐剑,段哲民.卡尔曼预测器在目标相关跟踪中的应用[J].计算机仿真,2005,22(11):120-122.
[8] 宋宇.基于四元数EKF算法的小型无人机姿态估计[J].吉林大学学报(理学版),2015,53(3):511-518.
[9] 冀亮.基于四元数的四轴无人机姿态的估计和控制[J].现代电子技术,2015,38(11):112-115.
[10] 杨蒲,李奇.三轴陀螺稳定平台控制系统设计与实现[J].中国惯性技术学报,2007,15(2):171-176.
[11] LEE B J, PARK J B, JOO Y H, et a1.Intelligent Kalman filter for tracking a manoeuvfing target[J].Iee Proceedings Radar Sonar & Navigation,2004,151(6):344-350.
[12] LEE J H,PARK K,YOU K H,et a1.Kalman filter applications to laser interferometer measurements in position-servo systems[J].Electronics letters,2006,42(17):969-970.

