基于解耦算法的电力系统准稳态的实现

(国网重庆市电力公司，重庆 400015)

电力系统电压稳定性是指在给定的初始运行条件下，遭受扰动后的电力系统在所有母线上保持稳定电压的能力[1]。它依赖于电力系统中保持或恢复负荷需求和负荷供给平衡的能力。电力系统的电压稳定性问题最早于20世纪40年代由马尔柯维奇提出[2]，且随着电网规模的不断扩大而日趋严重。在现代电力系统电压稳定性分析中，人们提出了多种基于连续算法的方法来研究电压稳定性的问题。然而，仍然需要通过时域仿真来捕捉系统的瞬态响应并把握控制系统操作的时机。时域响应可以捕捉系统不稳定过程中的变化，从而提出控制的时序问题；而为了捕捉到系统的瞬时响应，则需要对一组微分代数方程(DAE)进行求解[3-4]。电力系统典型网络中包含大量的动态组件和静态组件，而其中每个单独的组件都可能需要由数个微分代数方程组来表示。因此，一个真正的电力系统，需要很多个微分代数方程组。

对于复杂电力系统的动态组件和静态组件，其时间常数在一个较大的范围内变化时，会导致系统刚度问题的产生[5]。目前，时域模拟仿真中通常采用的数值方法会对刚性系统产生错误结果，这主要是由步进式的数值积分过程中误差的累积所导致的[6]。时域仿真分析中通常需要利用到数值积分法，这些积分方法主要可以分成两类，即显性算法和隐性算法。其中，显性算法涉及固定点迭代，运算速度较快，但在处理刚性问题时会存在数值稳定性问题；而隐性算法更具稳定性，但运算速度较慢。文献[7]指出，在采用显性算法的情况下需要通过显著地减小控制步长来保持数值稳定性。文献[8]则通过一个简单的两变量例子来说明显性算法与隐性算法对刚性系统的区别。本文在当前时域仿真分析所采用的数值积分法基础上，提出一种新的解耦仿真分析方法。此方法可用来解决电力系统中出现的刚度问题。然后，利用此解耦的时域仿真方法，讨论了准稳态(quasi-steady-state，QSS)仿真在考虑负载随时间变化的条件下的实现。最后，利用新英格兰39节点系统验证了此仿真方法的有效性。

1 解耦的时域仿真算法

对于电力系统，可以通过隐性算法来实现保持数值稳定性的步长控制。但由于隐性算法通常用来模拟动态特性，故每个方程的积分步骤，都涉及一个非线性方程的求解过程，从而导致一组线性问题的出现。因此，求解系统的算法需要通过大量的时间来求解系统的线性方程组。采用解耦的时域仿真方法的目的，就在于减小传统的隐性算法的计算量。事实上，时域仿真运算法则的数值稳定特性是由线性化矩阵的特征值所决定的，而通常引起刚性问题的特征值只占整个范围的一小部分。某一问题可以划分为刚性部分与非刚性部分，如式(1)所示

(1)

式中：xs，xn分别表示刚性变量与非刚性变量；fs，fn则代表刚性方程与非刚性方程。

那么，对这个系统的处理可以分为两个部分，即对刚性部分使用隐性算法，而对非刚性部分使用显性算法。

对于数值稳定性，它要求特征值位于某一稳定域内，方可产生收敛效果。若某些特征值是位于显性算法的稳定域外部，那么动态仿真的数值稳定性可能不会得到显示。但是，这些数值结果可以通过对处于稳定域外部的特征值进行不同的处理而得到修正。从几何学的角度来看，常微分方程(ODE)系统与DAE系统的解就是多维空间内的点或向量。可以把这个空间划分为两个或更多的子空间，而那些解向量也就可以分解为相应于每个子空间内的子向量。因而，通过把空间分解为若干子空间，把解向量分解为子向量，从而使原始的ODE系统与DAE系统也可以解耦为若干个小维度的系统。

假设P为对应位于某种显性算法稳定域之外的m个特征值的不变子空间，Z1为P内的一组标准正交基。因此，Z1是一个n×m的矩阵，且其满足下列条件：

(2)

这里Im是m×m的单位阵。

此外，还存在一个正交补Q，并设Z2为Q内的一组标准正交基，则

(3)

因为，Q是P的一个正交补，那么有

(4)

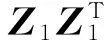
由于位于原始的n维空间内的向量可以分解为两个小维度的向量之和，那么原始系统也可以分解为两个子系统，即

(5)

ODE系统方程式可以解耦为：

(6)

通过对上述方程式的求解，可以分别计算出向量p和q，从而系统的初始状态可表示为：x=Z1p+Z2q。

可以看出，式(6)有着类似于式(1)的期望的形式，而且其第二组方程的所有特征值都位于稳定域内部。因此，可采用显性算法来求解第二组方程，用隐性算法来求解第一组方程。为了捕获长期的电压稳定的响应，人们提出了许多有效的算法，用以减少计算量，其中使用最广泛的方法就是准稳态时域仿真。

2 准稳态(QSS)仿真的实现

2.1 相关概念

准稳态是指在某些确定条件下系统响应的近似值。QSS仿真的基本思想是用一系列由长期动态过程驱动的短期平衡点来近似系统的长期动态过程，是潮流计算和全时域仿真的一种折衷。QSS仿真通过时标分解，分开求解暂态和中长期过程，协调了中长期仿真在计算速度和计算精确度两方面的矛盾。QSS近似基于如下假设：存在短期动态过程的稳定平衡点；短期动态过程在足够短的时间内达平衡点。QSS仿真具有不存在PV和Vθ假设，能够较准确地计及各种限制作用，能够反映控制作用和元件动作的时域规律，计算速度快，收敛性能好等优势，是中长期电压稳定分析的有力工具。

2.2 准稳态模型

在引入了稳态假设后，电力系统的动态过程可用具有连续-离散时间的微分-代数方程组表示

(7)

0=G(X，Y，zD，zC，λ)

(8)

(9)

zD(k+)=hD[x(k-)，y(k-)，zD(k)，λ(k)]

(10)

在式(7)中，函数F描述了同步机、励磁系统、原动机以及调速器的动力学，而式(8)中的函数G则代表了系统网络功能。式(7)和式(8)分别包含了瞬态变量X与代数变量Y。变量Y通常与网络母线电压的幅值和相角有关。长期动态响应通过式(9)和式(10)中的离散的或/和连续的时间变量来捕获。zC为连续状态变量列向量，代表了连续负载的恢复动态；zD为离散状态变量列向量，与发电机过励限制及定子过流限制相关；式中的λ表示了负荷需求的变化以及相应的电源延时。

2.3 QSS仿真思路

基本的QSS仿真原理如图1所示。A点是出现干扰之前的平衡点，而A′是这些方程式在受到干扰之后的平衡点。从A′到B的连续变化是由于λ和zC的变化所引起的，从B到B′的过渡则来自于zD的不连续改变。

图1 准稳态仿真原理

点A′和B′处的状态为固定zC和zD于当前值下式(7)、(8)的解所对应的状态，表示设备动作后系统的暂态平衡点。点A′至B以及点B′至C处的状态变化对应于式(9)所描述的系统慢动态变化，或系统某些参数的变化(如系统负荷的增加)。通过联立求解式(7)～(9)，可获得点B，C处的状态。再结合系统的准稳态模型，将式(9)差分化后，可以求得在zD固定的情况下暂态平衡点B，C处的状态。

2.4 考虑负载变化下QSS仿真的实现

最基本的QSS仿真分析中并没有包含对于时间的积分，但却能够在平衡跟踪期间间接地得到时间信息，这些时间信息基于离散控制的内部延迟。过渡时间步长s=tk+1-tk是由最短内部延迟或长期组件的采样周期zD所决定的。更具体地说，在这个时间步长内，会根据一些控制逻辑进行修正。连续潮流算法中介绍了参数λ，它可以对步长控制下的系统平衡进行跟踪。在变压器有载调压分接开关(OLTC)工作的过程中，λ也会根据时间特性进行变化。应当通过适当地考虑λ在固定的时间间隔tk+1-tk内的变化，以满足相应的时间函数。

(11)

(12)

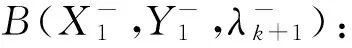
(13)

式中，步长是σk。

(14)

一般来说，在每个时刻，控制步长都应重新计算以适合负荷在这一时期的变化。注意到作用于修正阶段的雅可比行列式取决于来自预测阶段的状态变量。为了得到用于步长计算的dλ和Δλ，首先将作用于预报器的雅可比行列式同样作用于校正器。在得到近似步长以后，对校正器里的雅可比行列式进行修正，通过求解式(12)得到新的Δλ，并利用式(14)再次计算步长，重复这个过程直到修正的Δλ值与原来值之间的误差在允许范围内为止。

3 系统仿真实例

3.1 基本概况

图2所示为新英格兰10机39节点测试系统的单线图，前文提到的完全显性前向欧拉算法和完全隐性梯形图解法等算法均可应用于此系统。在此情况下，每台发电机有9种状态，微分状态和代数状态的总数分别是90和78。仿真过程中的步长选择0.025 s，刚性不变子空间是在19维度的初始状态下计算的，对于使用的解耦算法，系统的非线性方程式的维数是97。与此同时，对于完全显性算法和完全隐性算法，非线性系统的维度分别是78和168。

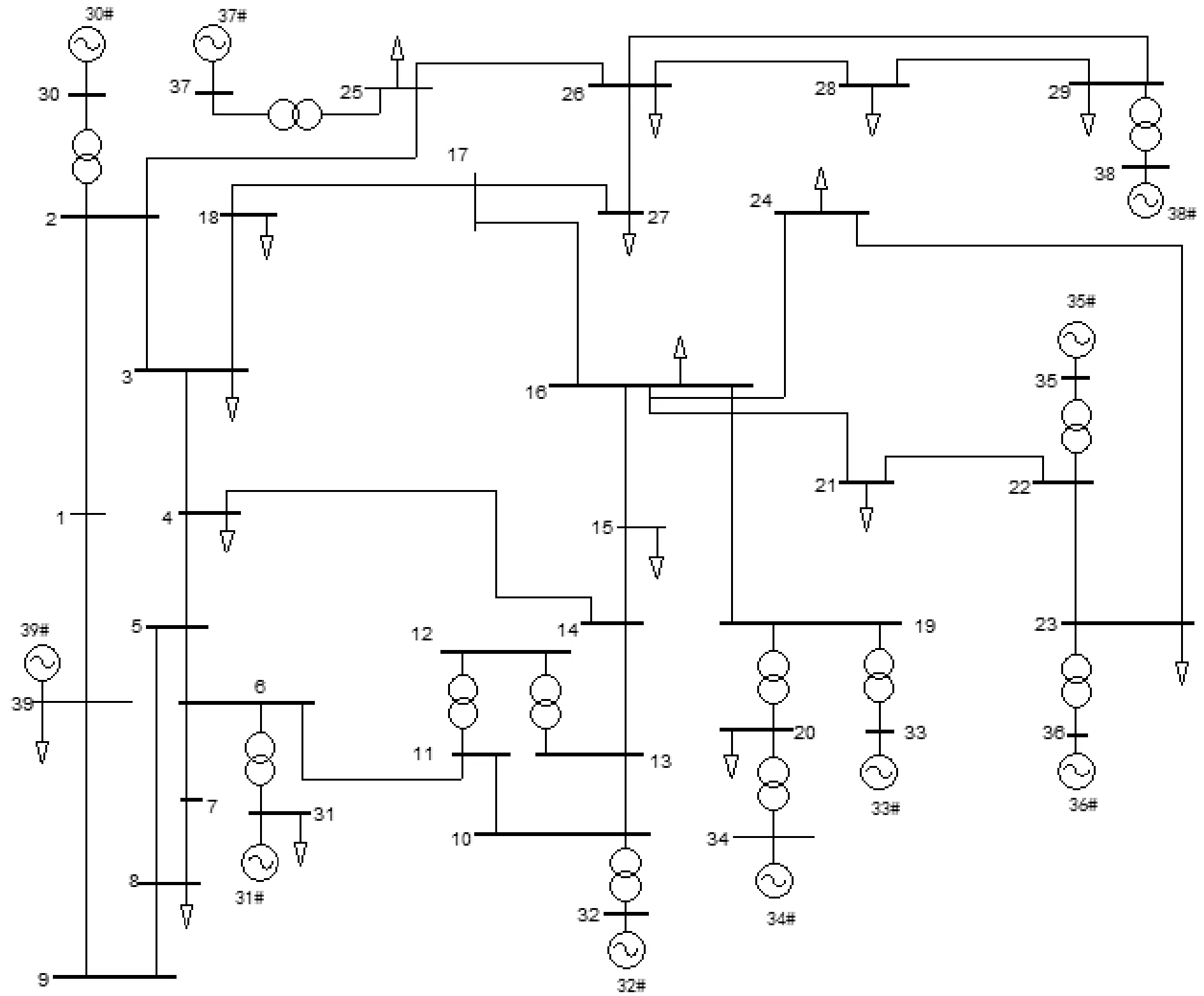
图2 新英格兰39节点系统单线图

3.2 线路跳闸事故的时域仿真

本仿真选取意外事故是6#母线和7#母线之间的线路在0.05 s时发生线路跳闸，仿真时间是20 s，分别采用完全显性算法、完全隐性算法和解耦算法进行仿真。仿真结果如图3至图5。实际中要求干扰后的响应使系统可以保持其稳定性，但由仿真图3至图5可以看出，在解耦算法与完全隐性算法产生稳定结果的情况下，完全显性算法未能给出理想的结果。

图3 完全显性算法的仿真结果

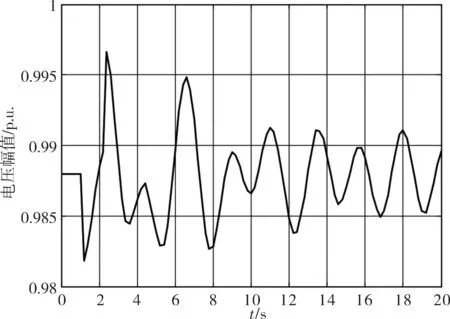
图4 完全隐性算法的仿真结果

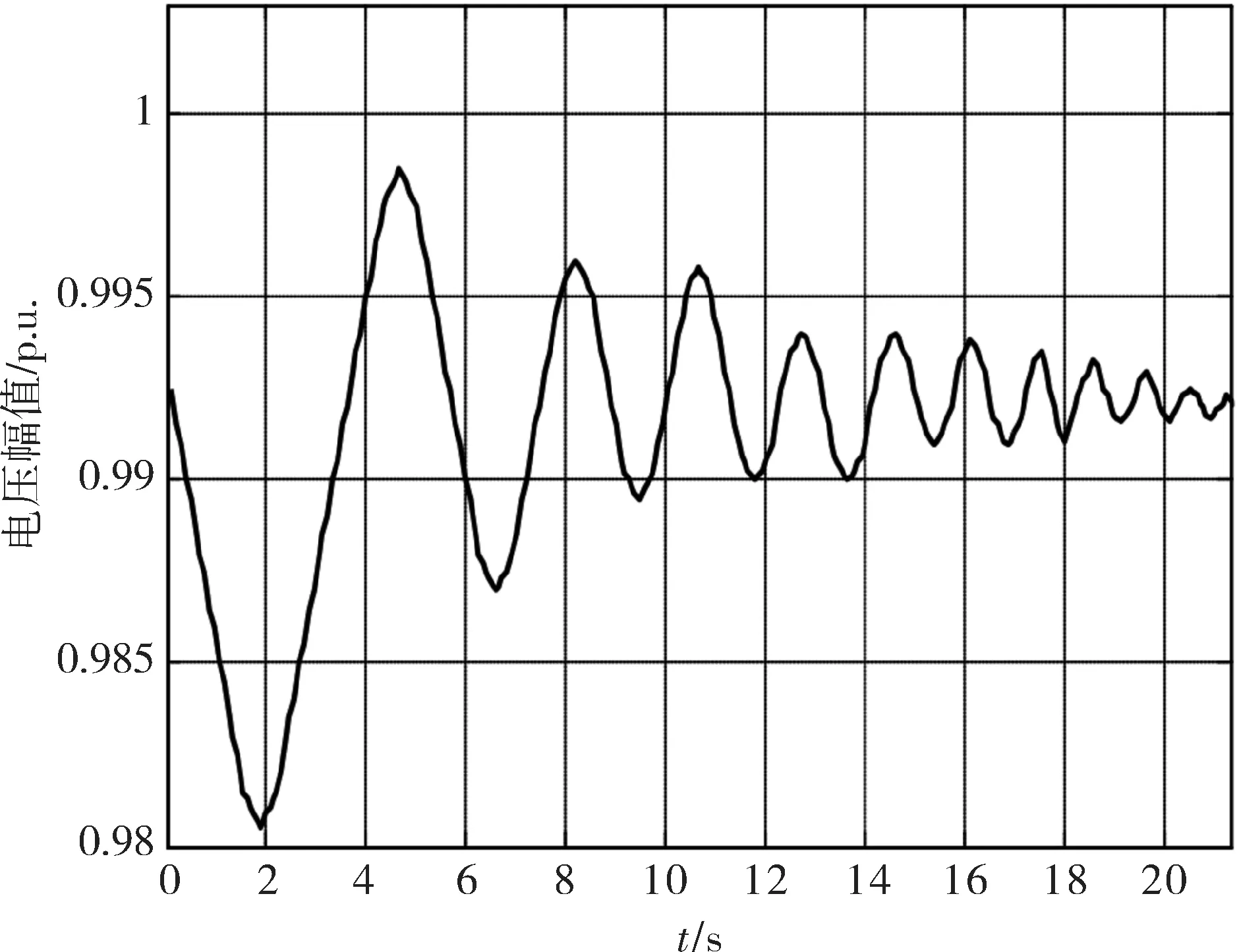
图5 解耦算法的仿真结果

由图3可以看出，完全显性算法(采用纯粹前向欧拉算法)的结果大约在1s时出现分岔，导致动态仿真无法完成，而在显性算法分岔之前，可以观察到一个振荡行为，这只是由数值取值的原因引起的，而并不代表实际的系统响应。

与此同时，完全隐性算法与解耦算法的仿真结果给出了稳定的系统响应，分别如图4和图5所示。这两种算法都给出了系统受干扰后的稳态响应，而且这两种算法的结果也较好地匹配了系统运行结果。从仿真结果可以看到，系统扰动后暂态过程很快平息，达到一个新的暂态平衡点。此后，系统逐步向临界点逼近的驱动力即为OLTC的动作和由选定增长方式确定持续增加的负荷。对两种算法下的仿真结果进行比较可知，图5所示的解耦算法仿真曲线比图4 所示的完全隐性算法仿真曲线更理想。

3.3 负荷逐渐增加的长期时域仿真

设定与6#母线通过变压器相连的31#母线负载以每秒0.5%的速率增加，以捕获长期的系统不稳定的响应。6#母线电压的仿真结果如图6所示。由仿真结果可以看出，解耦算法综合了完全显性算法与完全隐性算法的优点，既可以得到数值计算的稳定性，又具有很高的效率。在使用这种方法时，刚性与非刚性的子空间是分开考虑的，而且是用不同的算法处理的。然而，和任何时域分析算法一样，它仍然需要相当数量的CPU时钟来获取相关的系统响应，尤其是对于中长期电压稳定的仿真。

图6 负载增长情况下的长时期仿真结果

4 结论

本文对采用准稳态假设后的中长期电压稳定的仿真算法进行了研究，在当前时域仿真分析中，根据数值积分法提出一种新的解耦仿真算法。此算法综合了显性算法和隐性算法的期望特性，在保证数值计算结果稳定性的同时，又具有良好的运算效率。利用此解耦的时域仿真方法，讨论了QSS仿真在考虑负载随时间变化条件下的实现，并利用新英格兰39节点系统验证了此仿真方法的有效性。仿真算例表明，提出的解耦算法可以帮助QSS仿真追踪系统中长期动态过程，在负荷需求增加导致的崩溃点附近也有较好的数值性能，可以较为准确地得到中长期电压稳定的极限点。

参考文献：

[1] 周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社, 2004 .

[2] 苏永春,程时杰,文劲宇.电力系统电压稳定性及其研究现状(一) [J].电力自动化设备,2006,26(6): 97-101.

[3] 陈文广,刘明波,林声宏,等.长期电压稳定准稳态仿真算法比较[J].电网技术,2009,33(9):44-51.

[4] 安宁,周双喜,朱凌志.中长期电压稳定准稳态时域轨迹追踪方法[J].电网技术,2006,30(20):40-45.

[5] 胡扬宇,吕天光,褚双伟，等.基于准稳态仿真的电压稳定轨迹灵敏度分析方法[J].电网技术,2012,36(6):157-162.

[6] 徐泰山,鲍颜红,薛禹胜,等.中期电压稳定的快速仿真算法研究[J].电力系统自动化,2000,24(24): 9-11.

[7] DEUFLHARD P, BOMEMANN F.Scientific computing with ordinary differential equations[M].New York: Springer New York,2002.

[8] ISERLES A. A First course in the numerical analysis of differential equations[J]. American Journal of Physics, 1998, 65(5):929.