具有低开关频率的三电平有源前端变换器模型预测控制

杨 瓅1，黄正波2，王虹淋

(1.重庆电力高等专科学校，重庆400053；2.国网重庆市电力公司 北碚供电分公司，重庆400070；3.陆军勤务学院训练基地，湖北 襄阳441000)

三电平有源前端变换器(active front-end rectifiers, AFEs)已广泛应用于可再生制动电机驱动领域[1-4]。为了改进回馈电能的质量，满足网侧较低谐波畸变率(total harmonic distortion, THD)的标准，相较于两电平变换器，三电平AFEs具有以下优点：能量的双向流动；可控的功率因数；高质量的直流侧输出电压；较低的网侧电流THD。然而，随着工业技术的进步和人类社会的发展，人们对现代三电平AFEs控制系统提出了越来越多的设计要求。

随着对三电平AFEs的深入研究，许多新颖的控制策略被提出，包括有限控制集模型预测控制(finite-control-set model predictive control, FCS-MPC)[5-7]、无差拍预测直接功率控制(dead-beat predictive direct power control, DB-PDPC)[8]、滑模控制(sliding-mode control, SMC)[9]等。在以上控制策略中，FCS-MPC算法具有简单的控制器设计方案，并将完整的模型预测控制(model predictive control, MPC)方案引入变流器控制中，控制系统包含预测模型、滚动优化、计算求解3个部分，具有结构简单、动态响应迅速、控制灵活等特点，近年来被广泛地研究与应用。

然而，在高压大功率应用领域的相关研究则比较少。此外，功率器件开关频率过高将导致器件换向损耗增大及局部过热损坏的问题，将会降低其输出的最大功率[10]。因此，研究其系统在低开关频率下的控制性能显得尤为重要。为了降低开关频率，不同的策略被相继提出。文献[11]提出了一种应用于中压大功率电力传动系统的低开关频率广义最优脉宽调制方式。该策略的控制思想是在同步最优脉宽调制的基础上，使最大开关频率值最低，从而在减少电机定子侧电流畸变的同时，降低功率变换器的开关频率，缓解了开关频率过高导致开关损耗过大的问题。文献[12]提出了一种应用于大功率电流源电机驱动系统的低开关频率的混合脉宽调制策略。该策略在低开关频率的基础上，有效抑制了LC谐振问题；同时，为了改善电流谐波质量，引入了特定谐波消除技术，从而使系统性能得到有效改善。文献[13]提出了一种九电平级联逆变器的低开关频率最优脉宽调制技术。该策略在减小隔离直流电压源数量的基础上，能够有效抑制电流谐波，降低开关频率，并保持直流母线电容电压平衡。文献[14]提出了一种中压型大功率七电平级联5/3H逆变器的低开关频率最优脉宽调制技术，从而有效避免开关频率过高导致开关损耗过大的问题。以上方法能够成功降低开关频率，有效减少开关损耗。然而，较低的开关频率将降低系统的控制性能。

为解决以上矛盾，本文研究了一种改进的三电平AFEs低开关频率有限控制集模型预测控制(low switching frequency finite-control-set model predictive control, LFCS-MPC)策略。该策略在一个控制周期内同时施加有效电压矢量和零电压矢量，通过坐标变换构建α-β坐标系下三电平AFEs的预测模型，引入降低平均开关频率控制目标项；并基于该目标函数求得有效电压矢量的最优作用时间，从而将带有最优作用时间的开关状态直接作用于功率变换器。该方法在兼顾控制性能的同时有效地降低功率器件平均开关频率，实现了低开关频率下三电平AFEs的高效运行，而无需使用复杂的坐标变换、电流滞环以及脉宽调制模块。最后，建立了具有低开关频率的LFCS-MPC仿真模型，并对该算法的稳态与动态性能等方面进行分析。仿真结果表明，该方法在实际工程应用中具有一定的价值。

1 三电平有源前端变换器数学模型

图1为本文所研究的三电平AFEs拓扑结构。图中：eg，x为网侧电压(x=a,b,c，下同)；ig，x为网侧电流；vg，x为三电平AFEs输出电压；Lg，x为网侧电感；Rg，x为网侧电阻；C1，C2为直流侧上下两个电容所对应的飞跨电容(flying capacitors, FCs)；Ud，c1，Ud，c2为直流侧上下两个串联飞跨电容的电压 (FCs voltages)；id，c1，id，c2分别为流过C1，C2的电流；Udc为直流侧电压；O为直流侧中点。

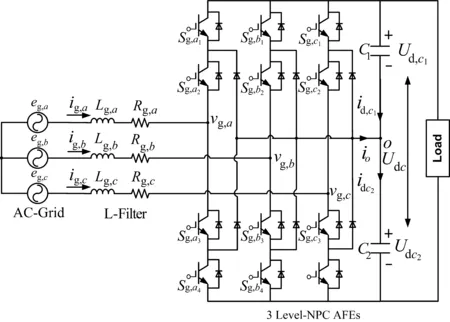
图1 三电平有源前端变换器并网变换器拓扑

定义三电平AFEs开关函数为

三电平AFEs开关函数Sg，x与三电平AFEs交流侧输出三相电压之间的关系可以表示为

假设系统为三相平衡系统，由图1电路结构可知，根据基尔霍夫电压定律(kirchhoffvoltage law, KVL)，建立α-β静止坐标系下三电平AFEs的连续时域内数学模型的表达式为

假定采样周期足够小(Ts≤20 μs)，那么利用向前欧拉公式，在一个采样周期中，式(3)中的微分项可以近似表示为

将式(4)代入式(3)，从而可以获得在α-β静止坐标系下三电平AFEs的离散时域内的数学模型表达式，即k+1时刻网侧电流预测值为

进一步可以求得直流侧电容分别所对应的电压离散数学模型，即k+1时刻直流侧电容电压预测值分别为

对于三相平衡系统，网侧有功功率与无功功率在k+1时刻的预测值分别为[15]

=1.5(eg，αig，α+eg，βig，β)

(8)

=1.5(eg，βig，α+eg，αig，β)

(9)

式(8)和式(9)中，eg(k+1)为k+1时刻的网侧电压预测值。假设采样周期Ts足够小，那么在一个采样周期中，eg(k+1)≈eg(k)。

以最小化功率跟踪误差为控制目标，构建的目标函数定义为

2 改进的低开关频率模型预测控制

由于传统FCS-MPC策略存在过高的开关频率，将增加功率器件的损耗，降低其效率。因此，为了解决这一缺陷，一种改进的LFCS-MPC策略被提出。该策略在目标函数中引入降低平均开关频率目标项，在兼顾控制性能的同时有效地降低功率器件动作频率，而无需使用复杂的坐标变换、电流滞环以及脉宽调制模块。具体控制系统框图如图2所示。

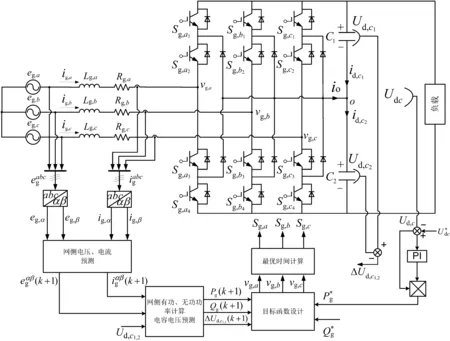
图2 改进的LFCS-MPC策略系统框图

本文所提出的目标函数设计，考虑以下4个控制目标：有功功率跟踪控制；无功功率跟踪控制；电容电压平衡；低开关频率控制。

为此，本文针对以上4种控制目标建立目标函数，从而完成相应的控制策略。目标函数式(10)被重新定义为

其中，

式中：NS为换相数量；λ1，λ2为权重因子，权重因子对系统性能起到关键作用。然而，权重因子的选择依然是一个开放问题，大多数情况下仍然采用经验的方式进行配置。当λ1较大时，系统侧重于电容电压平衡控制；当λ2较大时，系统侧重于降低开关损耗控制。因此，根据不同的需求来选择适当的权重因子。

在传统的FCS-MPC策略中，有效电压矢量直接作用在整个采样周期，如果采样周期较短，那么控制性能较好，开关频率较高。反之，如果采样周期较长，那么系统控制性能将有所降低。为了有效解决这个矛盾，本文提出了一种具有双矢量的LFCS-MPC策略。该策略是在一个采样周期中通过插入一个零电压矢量，基于目标函数式(10)，并依据功率脉动最小化原理，求得每个有效电压矢量所对应的最优作用时间，最终将最优作用时间下的有效电压矢量与零矢量作为控制器的输入。其具体过程如图3所示。

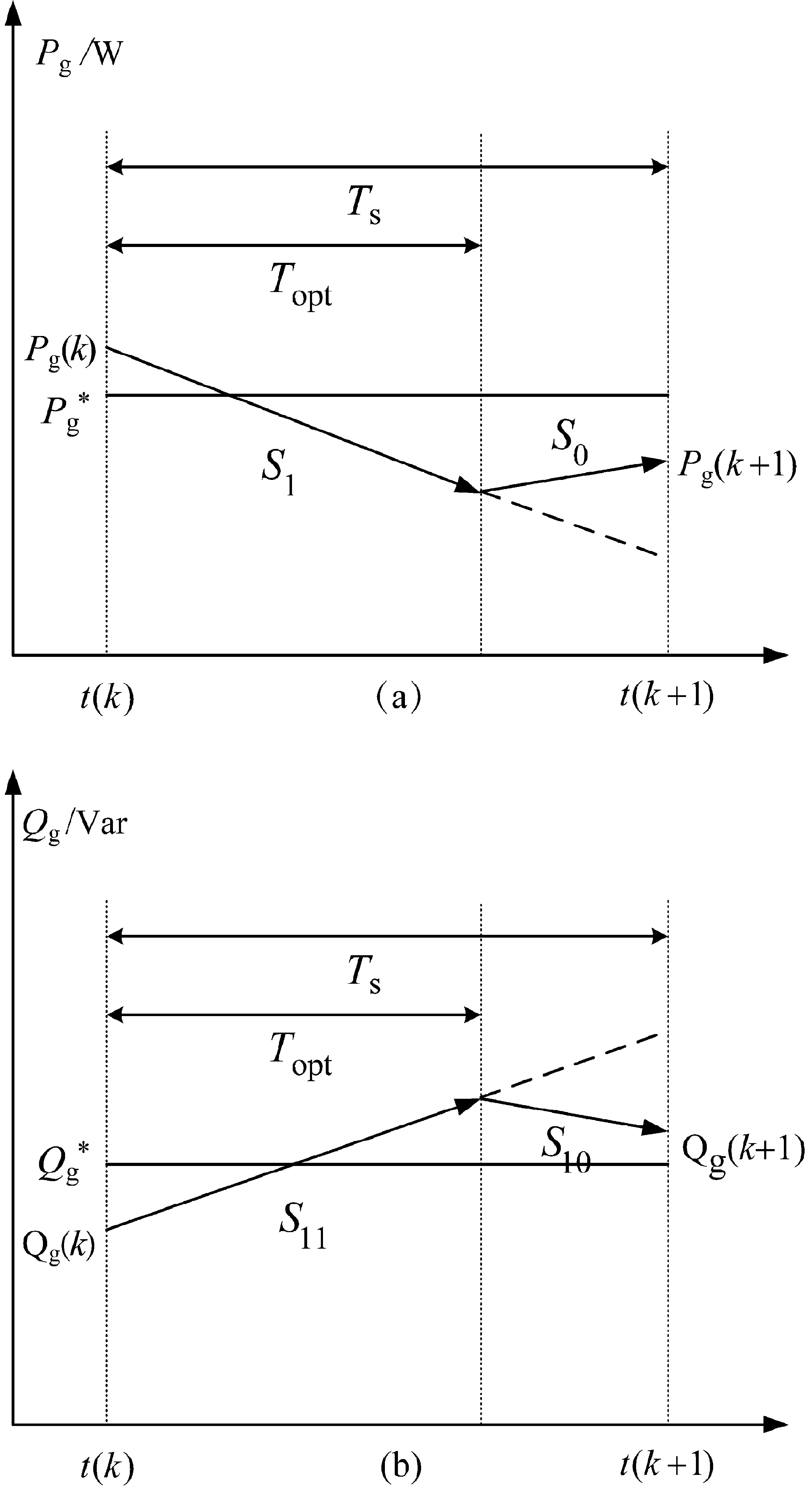
图3 功率脉冲最小算法图

假设三相电网电压平衡且正弦，有功与无功功率的斜率可以表示为

式中：S1和S0分别为有功功率在有效电压矢量和零电压矢量作用下的斜率；S11和S10分别为无功功率在有效电压矢量和零电压矢量作用下的斜率；ω1为网侧电压角频率。

根据图3所示，那么，有功与无功功率的预测值将改为

Pg(k+1)=Pg(k)+S1T1+S0(Ts-T1)

(17)

Qg(k+1)=Qg(k)+S11T1+S10(Ts-T1)

(18)

基于目标函数式( 10) ，根据功率脉动最小化原 理，通过对目标函数求g1 偏导(g1/t=0) ，将式 (17) 、(18) 带入式(10) ，从而求得有效电压矢量的 最优作用时间为[16]

其中，零电压矢量的作用时间为T0=Ts-T1。

其中，零电压矢量的作用时间为T0=Ts-T1。

3 仿真结果

3.1 模型系统参数

为验证改进LFCS-MPC策略的有效性，本文利用MATLAB/SIMULINK搭建了三电平AFEs的LFCS-MPC策略系统模型。该仿真模型系统参数见表1。

表1 LFCS-MPC控制器参数表

3.2 稳态特性对比

图4和图5分别为传统FCS-MPC方式以及所提出的LFCS-MPC策略下的稳态性能仿真波形。其中，图4(a)和图5(a)分别为网侧有功功率Pg和无功功率Qg稳态仿真波形。从图中可以看出，在两种控制方式下，实际的有功功率与无功功率可以准确地跟踪功率参考值，且具有相对较小的功率脉动。图4(b)和图5(b)分别为静止α-β坐标系下网侧电压与电流波形。从图中可以看出，网侧电流与电压同相，保持单位功率运行。同时，传统FCS-MPC策略下的网侧电流THD为2.84%，所提出的LFCS-MPC策略下的网侧电流THD为3.18%。

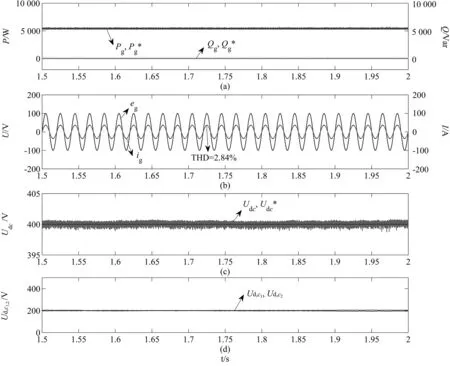
图4 传统FCS-MPC策略下的稳态性能仿真波形

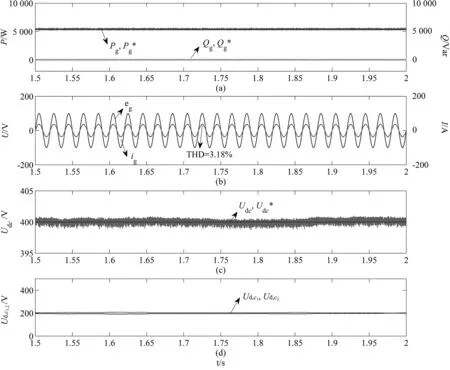
图5 改进LFCS-MPC策略下的系统稳态性能仿真波形

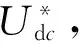
3.3 动态特性对比

图6和图7分别为传统FCS-MPC以及所提出的LFCS-MPC策略下的暂态性能仿真波形。其中图6(a)和图7(a)分别为网侧有功功率Pg和无功功率Qg的稳态仿真波形。从图中可以看出，在两种控制方式下，实际的有功功率与无功功率可以准确地跟踪功率参考值，具有较快的暂态响应，且具有相对较小的功率脉动。图6(b)和图7(b)分别为静止α-β坐标系下网侧电压与电流波形。从图中可以看出，当直流母线电压发生阶跃变化之前，传统的FCS-MPC策略的网侧电流THD为2.84%，所提出的LFCS-MPC策略下的网侧电流THD为3.18%；在直流母线参考值电压发生阶跃变化之后，传统的FCS-MPC策略的网侧电流THD为1.86%，所提出的LFCS-MPC策略下的网侧电流THD为2.31%，符合IEEE标准。

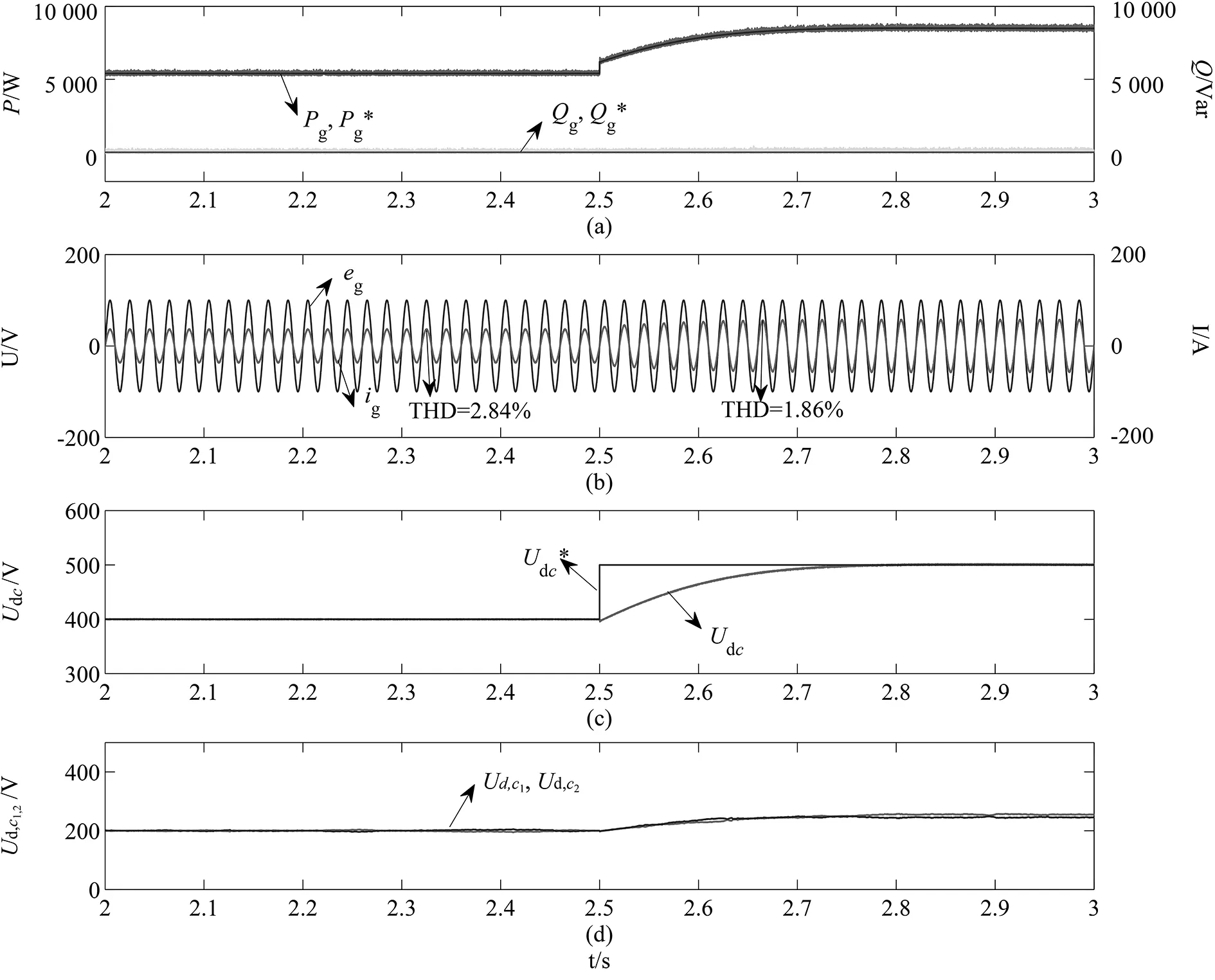
图6 传统FCS-MPC策略下的暂态性能仿真波形

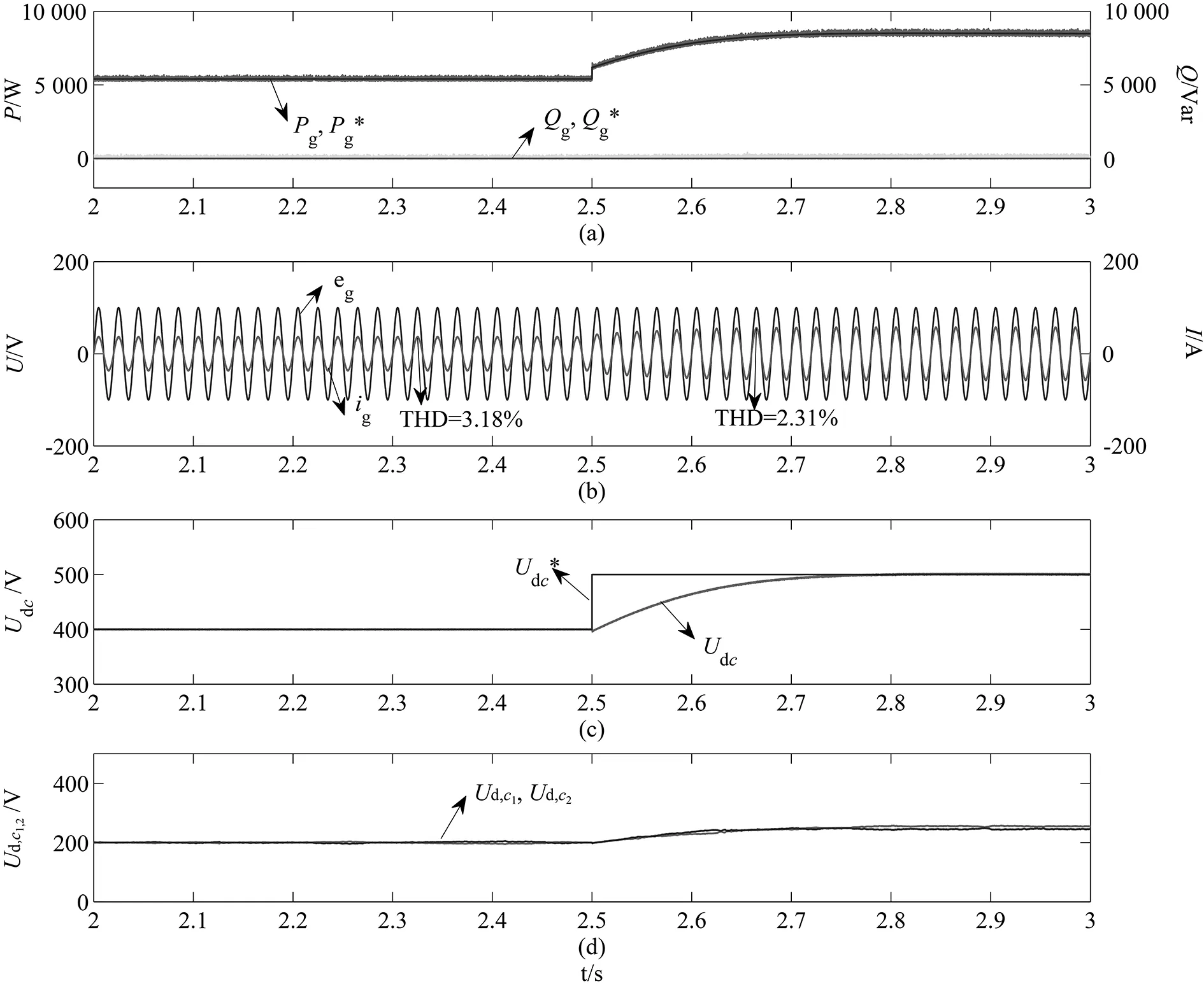
图7 改进LFCS-MPC策略下的系统暂态性能仿真波形

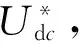
4 结论

本文以三电平AFEs为研究对象，提出了一种改进的三电平有源前端变换器LFCS-MPC策略。仿真结果证明，所提出的FCS-MPC策略平均开关频率相对较低，然而，网侧电流THD相对较高。最后，两种方法都可以在直流母线电压发生突变的情况下，使系统快速达到稳定且较好的控制效果。综上所述，所提出的LFCS-MPC方式能够在兼顾控制性能的同时，有效地降低功率器件平均开关频率，实现了低开关频率下三电平AFEs的高效运行，并在实际应用中具有一定的借鉴性。

参考文献：

[1] 张颖超,赵争鸣,冯博,等.三电平双PWM变频器综合控制策略[J].电工技术学报,2011,26(11):25-31.

[2] YARAMASU V,WU B,ALEPUZS,et al.Predictive control for low-voltage ride-through enhancement of three-level-boost and npc-converter-based pmsg wind turbine[J].IEEE Transactions on Industrial Electronics,2014,61(12):6 832-6 843.

[3] HABIBULLAH M,LU D C,XIAO D,et al.Predictive torque control of induction motor sensorless drive fed by a 3l-npc inverter[J].IEEE Transactions on Industrial Informatics,2017,13(1):60-70.

[4] HABIBULLAH M,LU D C,XIAO D,et al.Finite-state predictive torque control of induction motor supplied from a three-level npc voltage source inverter[J].IEEE Transactions on Power Electronics,2016,32(1):479-489.

[5] SCOLTOCK J,GEYER T,MADAWALAUK.Modelpredictive direct power control for grid-connected npc converters[J].IEEE Transactions on Industrial Electronics, 2015，62(9):5 319-5 328.

[6] XIA C, LIU T, SHI T, et al. A simplified finite-control-set model-predictive control for power converters[J].IEEE Transactions on Industrial Informatics,2014,10(2):991-1 002.

[7] ZHANG Y,PENG Y.Performance evaluation of direct power control and model predictive control for three-level AC/DC converters[C]//Energy Conversion Congress and Exposition. IEEE,2015:217-224.

[8] SONG W,MA J,ZHOU L,et al.Deadbeat predictive power control of single-phase three-level neutral-point-clamped converters using space-vector modulation for electric railway traction[J].IEEE Transactions on Power Electronics 2016，31(1):721-732.

[9] SEBAALY F,VAHEDI H,KANAAN H Y,et al.Design and implementation of space vector modulation-based sliding mode control for grid-connected 3l-npc inverter[J].IEEE Transactions on Industrial Electronics 2016,63(12):7 854-7 863.

[10] EdpugantiA,Rathore A K.A survey of low-switching frequency modulation techniques for medium-voltage multilevel converters[C]//ndustry Applications Society Meeting.IEEE, 2015:4 212-4 228.

[11] RATHORE A K,HOLTZ J,BOLLER T.Generalizedoptimal pulse-width modulation of multilevel inverters for low-switching-frequency control of medium-voltage high-power industrial ac drives[J].IEEE Transactions on Industrial Electronics, 2013, 60(10):4 215-4 224.

[12] WANG Z, WU B, XU D, et al.Hybridpwm for high-power current-source-inverter-fed drives with low switching frequency[J].IEEE Transactions on Power Electronics,2011, 26(6):1 754-1 764.

[13] EDPUGANTI A,RATHORE A K. Optimal low switching frequency pulse-width modulation of nine-level cascade inverter[J].IEEE Transactions on Power Electronics,2014, 30(1):482-495.

[14] EDPUGANTI A,RATHORE A K.Optimal Low-Switching Frequency Pulsewidth Modulation of Medium Voltage Seven-Level Cascade-5/3H Inverter[J].IEEE Transactions on Power Electronics,2015,30(1):496-503.

[15] PENG F Z,LAI J S.Generalized instantaneous reactive power theory for three-phase power systems[J].IEEE Transactions on Instrumentation & Measurement,1996, 45(1):293-297.

[16] 张永昌,谢伟,李正熙.PWM整流器功率脉动最小化方法的研究[J].中国电机工程学报,2013,33(18):57-64.