CDC—代数上中心化映射的刻画
马 飞,赵健堂,郑 欣
设A是一个环或代数,若可加映射φ:A→A满足 ∀a,b∈A ,有 φ(ab)=φ(a)b(φ(ab)=aφ(b)),则称 φ是一个左(右)中心化子。既是左中心化子又是右中心化子的映射称为中心化子;∀a∈A,有φ(a)a-aφ(a)∈Z(A)(Z(A)为 A的中心),则称φ是中心化映射;如果φ(a)a=aφ(a),则称映射φ可交换。
关于映射在哪些条件下是中心化子一直是国内外学者们研究的热点问题。如在文献[1]中证明了半素环R上的映射φ既是左、右Jordan中心化子是中心化子;文献[2]中研究了特征不为2的自由半素环 R上的可加映射 φ若满足 ∀a∈R,有2φ(a2)=φ(a)a+aφ(a),则 φ 是中心化子;文献 [3]中证明了特征不为2的素环上的可加映射φ,若满足∀a∈R,n≥2都有φ(an)=φ(a)an-1,那么φ是左中心化子;文献[4-5]也研究了相关内容,并最终得到了标准算子代数上满足φ(Am+n+1)-Amφ(A) An∈FI(其中m,n为正整数),则存在数域F中的常数λ,使得对任意的a∈A,有φ(a)=λa。我们在文献[6]的基础上中将齐霄霏的结果推广到了任意的完全分配可交换子空间格代数上。
1预备知识
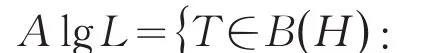
下面我们来介绍几个与本文证明有关的引理:
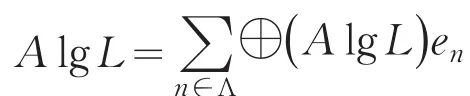
引理2[10-11]设A lg L是Hilbert空间H上的不可约CDC-代数,则存在一个非平凡投影e∈L,使得e(A lg L) e⊥是忠实的A lg L-双边膜。即对于任意的 A∈A lg L,如 果 Ae(A lg L) e⊥={0} ,则 有Ae=0;如果e(A lg L) e⊥A={0} 成立,则有e⊥A=0。
从文献[12]中可知,CDC-代数由其本身所包含的秩一算子弱*闭生成的;而文献[10-11]分别探究了线性导子以及线性Lie导子、CDC-代数上的代数同构。在CDC-代数A lg L中,设U(L)={e∈L:e≠0,e-≠H } ,若存在e1,e2,…,en∈U(L ),使得ei与ei+1可比,e0=e,en+1=e'(i=0,1,…,n ),那么就称U(L ) 中的e,e'是连通的。存在C⊆U(L),如果C中的任意两个元素都是连通的,并且C中的任意一个元素与U(L)C都不连通,那么就称C为U(L)的连通分支。令L是复可分的Hilbert空间H上的一个完全分配的交换子空间格。由于当且仅当A lg L的交换子是平凡的时候,A lg L是不可约的,即A lg L的一次换位是FI,也算子为I。
2主要定理及证明
下面我们先来研究比较简单的情形,即在不可约CDC-代数上的中心化映射的刻画。因为不可约CDC-代数的中心是平凡的FI,因此我们有下面的结论。
定理1设Φ:A lg L→A lg L是复Hilbert空间H上的不可约CDC-代数,对于A,B∈A lg L,都有
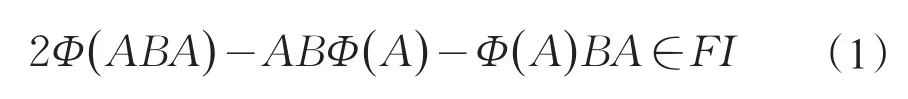
证明:根据基础知识与定义引理,我们分两种情况讨论。


本文主要研究完全分配可交换子空间格代数上的中心化映射。不失一般性,设所有的环和代数都是特征不为2的,并且记复Hilbert空间H中的恒等
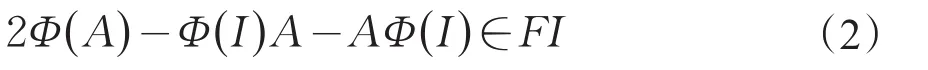
可用A+I代替A得

即存在 λA+I,λA,λB∈F,使得

断言1设Φ是满足式(1)的可加映射,则存在λ∈F使得对任意的幂等元e∈A有Φ(e)=λe。
式(2)中,给 A,I取值为e,则存在 λe∈F,即

对式(5)两边分别乘以e,有

给上式两边同乘以e,可知λee=0。




参考文献:
[1]BREŠAR M.Centralizing mappings on von Neumann algebras[J].Proceedings of the American Mathematical Society,1991,111(2):501-510.
[2]VUKMAN J,KOSI-ULBL I.On centralizers of semiprime of rings[J].Aequationes Math,2003,66(3):277-283.
[3]BENKOVIĆ D,EREMITA D.Characterizing left centralizers by their action on a polynomial[J].Publicationes Mathematicae,2004,64(3):343-352.
[4]VUKMAN J,KOSI-ULBL I.Centralizers on rings and algebras[J].Bull Austral Math Soc,2005,71(2):225-234.
[5]齐宵霏,杜栓平,侯晋川.中心化子的刻画[J].数学学报,2008,51(3):509-516.
[6]马飞,张建华,任刚练.完全分配可交换子空间格代数上的中心化映射[J].吉林大学学报(理学版),2017,55(1):48-54.
[7]DIXMIER J.Von neumann algebras[M].New York:North-holland,1981.
[8]LAMBROU M S.Complete distributivity lattices[J].Fundamenta Math,1983,119(3):227-240.
[9]GILFEATHER F,MOORE R L.Isomorphisms of Certain CSLAlgebras[J].JFunct Anal,2010,67(2):64-291.
[10]LU FY.Lie Derivations of Certain CSLAlgebras[J].Israel J Math,2006,155(1):149-156.
[11]LU FY.Derivations of CDCAlgebras[J].JMath Anal Appl,2006,323(1):179-189.
[12]LAURIE C,LONGSTAFF W E.A note on rank-one operators in reflexive algebras[J].Proc Amer Math Soc,1983,89(2):293-297.
[13]马飞.算子代数上的中心化子和高阶Jordan导子的研究[D].西安:陕西师范大学,2013.

