贮备系统的随机性比较
张晨霞,张正成,强玉霞
(兰州交通大学 数理学院,甘肃 兰州 730070)
在实际中,往往给系统配置一个贮备元件,以提高系统的可靠性。通常,贮备元件有3种贮备方式:冷贮备、热贮备和温贮备。在冷贮备下,贮备元件开始时是不运行的;在热贮备下,贮备元件在一般环境下是工作的,也就是说运行元件和贮备元件组成一个并联系统;而在温贮备中,贮备元件在更加温和的环境中工作,并且失效率比一般环境中的要小。贮备情况详见文献[1-2]。
在可靠工程系统中,冗余技术被广泛地应用到提高系统的可靠性中。事实上一个元件失效的确影响系统中的剩余元件的失效率。当系统的元件逐个失效时,系统中总的负载就得重新分配给剩余的元件,这就是负载共享系统。1971年Gross[3]观察了两个器官子系统后认为:人体的两个肾是负载共享系统的典型代表。
最近,Yun[4]研究了两个元件寿命是任意连续的随机变量的一般负载共享系统。假定这个系统的总负载为L,它被元件C1和C2共同分享。假定C1和C2的分配比例分别为α和1-α,特别地,当一个元件失效,另一个元件将负载该失效元件的负载。不失一般性假定L=1。Zhang等[5]提到元件C2(C1)可能被视为C1(C2)的一个备用负载元件,从中可以看出负载贮备是温贮备的一般化。
本文在可靠性的基础上,采用随机序的方法,对贮备系统的随机性进行研究,试图分析负载共享系统、温贮备系统、冷贮备系统、并联系统可靠性的优劣。
1预备知识
元件C1和C2在满负载条件下的寿命设为X和Y ,分布函数分别为 F(⋅)和 G(⋅),生存函数分别为Fˉ(⋅)和 Gˉ(⋅)。 XΡ1,YΡ2表示元件 C1和 C2在部分负载荷 Ρ1,Ρ2下的寿命,其分布函数分别为 FP1(⋅)和GP2(⋅),生存函数分别为 FˉP1(⋅)和 GˉP2(⋅)。 假定两元件在部分负载工作环境下的工作相互独立,特别地,在加速寿命模型中[6](或在减速寿命模型中[7])。假定对所有的t≥0
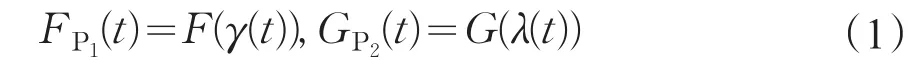
分配函数(i)γ(0)=0,λ(0)=0;(ii)对于所有的u≥0,γ(u)≤u,λ(u)≤u;(iii)γ(u)和 λ(u)在 u≥0上是单调递增的。事实上,式(1)揭示了在部分负载条件下比在满负载条件下元件的寿命要随机的大。

w(u)和v(u)分别是元件寿命X和Y在满载条件下的“虚拟寿命”[8-10],在部分负载条件下相应的正常寿命是u。换句话说,元件C1和C2的性能在部分负载条件(0 ,u]和在满载条件(0 ,w(u)]和(0 ,v(u)]下是一样的,且满足(i)v(0)=0,w(0)=0;(ii)对于所有的 u≥0,有 v(u)≤u,w(u)≤u;(iii)v(u)和 w(u)都在u≥0上是单调递增的。
如果假设元件C1在部分负载条件Ρ1下运行,然而C2在满负载条件下运行(即在通常条件下),负载共享系统就是温贮备系统。此时,用T(XΡ1,Y)表示温贮备的寿命,则X*表示温贮备元件在贮备状态时的寿命,分布函数为F(γ (⋅)) 。 其中 Xw(Y)=(X-w(Y)|X>w(Y))。当t≥0时,它的可靠度函数为
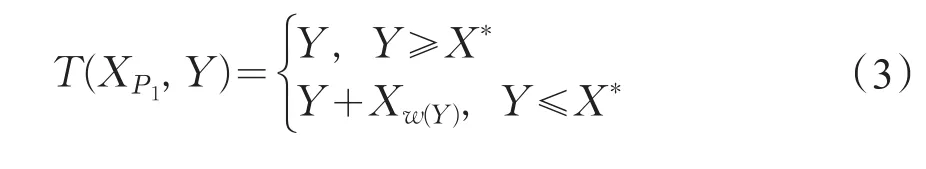
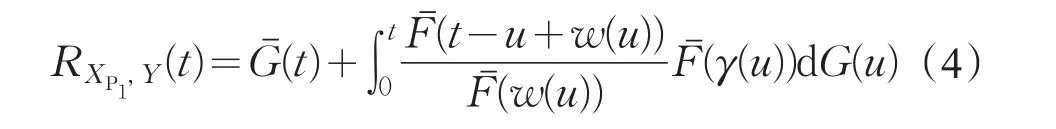
如果假设元件C1和C2都在满负载条件下运行(即在通常条件下),则温贮备系统就变成热贮备系统。在这种情况下,热贮备的寿命为max{X ,Y},其可靠度函数为
众所周知,元件C1和C2的冷贮备系统寿命的可靠度函数为
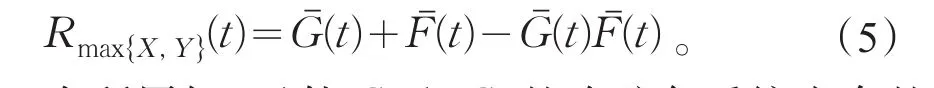
定义1:设X和Y是两个非负的随机变量,其分布函数分别是F(x)和G(x),密度函数分别为 f(x)和 g(x),生 存 函 数 分 别 为 Fˉ(x)=1-F(x)和。
x关于 递增,则称为X在失效率意义下小于Y,记作:X≤hrY。
关于更多的随机序参见文献[11-13]。
2主要结论及证明




设λ1=3,λ2=1和θ=5,λ3可以为任意值。对所有的t≥0,P(U2≥t)≥P(U1≥t)。得到U1≤stU2。由例2可得当定理6中的所有元件为指数分布,并在其他条件不变而加强假设Y1≤lrY2时,定理6的结果也无法得到改变。
4结语
本文主要讨论了由2个或3个元件组成的串联系统或并联系统的随机性质。以及研究一个冗余元件在并联系统中的最优分配问题。从而得知冷贮备系统比温贮备系统好、负载共享系统比温储备系统好等一系列结论;也得到把一个温贮备元件配置给一个反失效率序更大的运作元件可以提高系统的寿命。并讨论了元件寿命服从指数分布时系统可靠性的情况,并给出了例子进一步说明。
参考文献:
[1]SHEJ,PECHT M G.Reliability of a k-out-of-n warm standby system[J].IEEETrans Reliab,1992,41(1):72-75.
[2]FINKELSTEIN M S.On statistical and information-based virtual age of degrading system[J].Reliability Engineering and System Safety,2007,92(5):676-681.
[3]GROSSA J,CLARK V A,LIU V.Estimation of survival parameters when one of two organs must function for survival[J].Biometrics,1971,27(2):369-377.
[4]YUN W Y,CHA J H.A stochastic model for a general load-sharing system under overload condition[J].Applied Stochastic Models in Business and Industry,2010,26(5):624-638.
[5]ZHANG Z,BALAKRISHNAN N.Stochastic Properties and parameter Estimation for a general load-sharing system[J].Communication in Statistics-Theory and Mothods in Press,2017,46(2):747-760.
[6]BAGDONAVICIUSV,NIKULIN M.Accelerated Life Models:Modeling and Statistical Analysis[M].Florida:Chapman&Hall/CRC,2002.
[7]SINGPURWALLA N D.Survival in dynamic environments[J].Statistical Science,1995,10(1):86-103.
[8]Finkelstein M S.Mortality in varying environment[M]//Probability,Statistics and Modelling in Public Health.Springer US,2006:145-158.
[9]FINKELSTEIN M S.On statistical and information-based virtual age of degrading system[J].Reliability Engineering and System Safety ,2007,92(5):676-681.
[10]FINKELSTEIN M S.Virtual age of non-repairable objects[J].Reliability Engineering and System Safety,2009,94(2):666-669.
[11]SHAKED M,SHANTHIKUMAR J G.Stochastic orders[M].New York:Springer,2007.
[12]BLYTH C R.Some probability paradoxes in choice from among random alternative[J].American Statistical Association,1972,67(338):366-373.
[13]BOLAND PJ,SINGH H,CUKIC B.The stochastic precedence ordering with applicati-ons in sampling and testing[J].Journal of Applied Probability ,2004,41(1):73-82.

