CRH5动车组车轮低温概率疲劳寿命研究
杨柳青 胡 明 赵德明 周 迅 宋 浩 陈文华
浙江理工大学机械与自动控制学院,杭州,310018
0 引言
CRH5动车组主要运行在哈大高速铁路上,极端运行温度近-40℃,车轮在此低温条件下承受周期性的循环应力作用,易导致车轮发生疲劳失效[1-2]。概率疲劳寿命曲线作为研究疲劳寿命及评价疲劳可靠性的基础,其精确度的高低直接影响了寿命和可靠性评价结果的准确性。疲劳寿命曲线通常是通过试验方法获得的,传统疲劳理论认为当材料经过N=107次循环后仍未破坏时,就认为其可以承受无限次循环[3],故使用试验方法较易获得其中高寿命区间的概率疲劳寿命曲线(p-c-S-N曲线,p为存活率,c为置信度,S为应力幅值,N为疲劳寿命)。但是近年来大量研究表明,许多结构在N>107的超高寿命区间仍会发生疲劳失效[4]。本文所研究的动车组车轮的寿命包含超高周寿命区间;对于超高周寿命区间的p-c-S-N曲线,使用试验获得需要耗费大量的时间及精力,在实际情况下并不可行。目前,通常将试验获得的中高周疲劳寿命区间的曲线使用数学方法外推到超高寿命区间,从而获得完整的p-c-S-N曲线,即外推法。常用的外推方法有AASHO(American association of state highway and transportation officials)标 准 、ECCS(European convention for constructional steel work)标准以一致概率法(concurrent probabilistic method,CPM)。其中,AASHTO标准将中高段寿命区间的曲线直接用于超高周寿命区间,使用方便快捷;ECCS标准将中高段寿命区间曲线的斜率m在寿命N=5×106时变为 2m-1 进行外推,应用较广;ZHAO[5]使用一致概率法(CPM)将中高段寿命区间曲线外推至超高段,获得了较好的效果。由以上三种方法的对比可知,CPM方法具有最高的外推精确度,故本文使用CPM方法获得了ER8钢材在-40℃低温环境下的概率疲劳寿命曲线,并以此为基础,结合车辆系统动力学仿真及车轮有限元分析,计算了车轮的概率疲劳寿命。
1 试验与方法
本研究中,首先使用ER8材料试样进行疲劳试验,其次通过对试验数据统计处理获得中高寿命曲线,最后通过CPM外推法获得超高寿命曲线从而获得全寿命区间曲线。
1.1 ER8材料低温疲劳试验
ER8材料低温疲劳试验采用成组法[6]进行,试样为ER8材料制成的直径为8 mm标准疲劳试样,使用液压疲劳试验机在低温环境箱中进行对称拉压疲劳试验,试验温度为-40℃,共使用19根试样,试验结果见图1。另外使用升降法[7]测定材料疲劳极限S-1(S-1指应力比为-1时对称拉压循环下的疲劳极限),对应的疲劳寿命取N=5×106次循环,有效试样共7对(14根),试验结果见图2,其中,lgS是对数应力幅,lgN是对数循环周次。
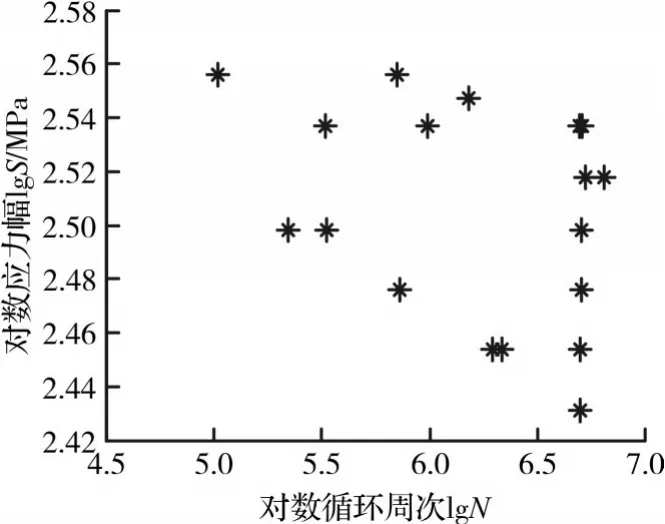
图1 ER8试样低温疲劳试验结果Fig.1 Fatigue test results of ER8 specimens at low temperature
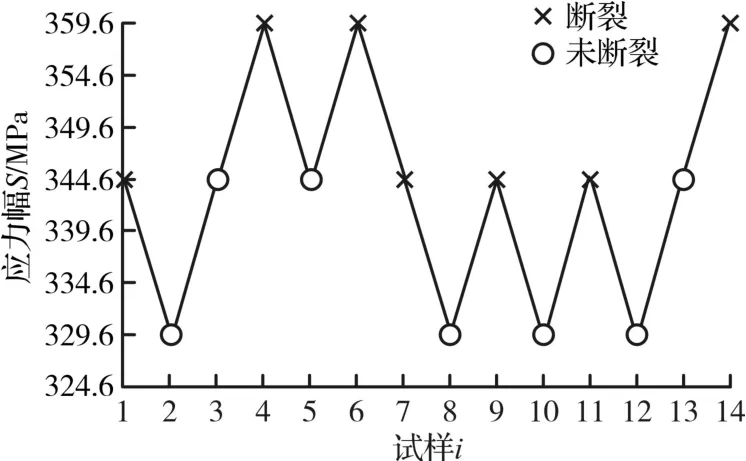
图2 ER8试样升降法试验结果Fig.2 Up and down test results of ER8
由图1可知,同一应力水平下,试样的疲劳寿命差异可跨越数量级,呈现出很强的分散性,所以单一的均值疲劳曲线不能描述这一分散性,而需要使用考虑统计特性的p-c-S-N曲线来描述其应力-寿命关系。
1.2 ER8材料低温环境下中高段寿命区间p-c-S-N曲线求解
对成组法获得的试验数据进行统计分析,可以得到ER8材料低温环境下的中高段寿命区间p-c-S-N曲线,以此作为材料超高寿命区间p-c-S-N曲线外推的基础。
幂形式的疲劳寿命曲线表达式如下:

式中,m、D为材料常数。
对式(1)两边取对数,并令 Y=lgN,A=lgD,B=-m,则有

据此,式(2)可改写为均值及均方差形式:

式中,Yμ和Yσ、Aμ和 Aσ、Bμ和 Bσ分别为Y、A、B的均值和均方差。
引入置信度c及存活率p,则任一p-c水平下的关系式为
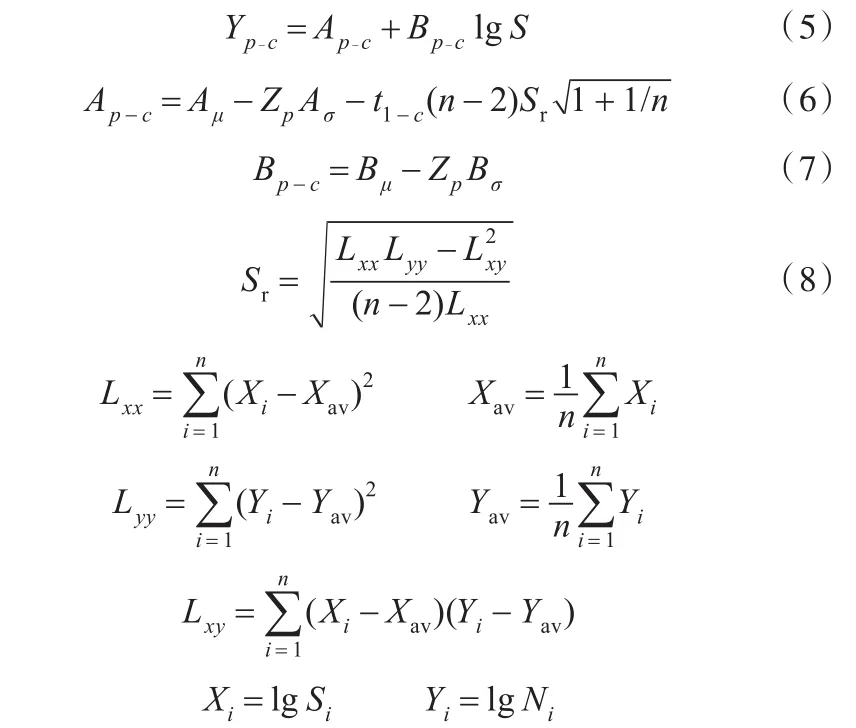
式中,n为疲劳试样数量;Zp为存活率为 p时的标准正态分布值;t1-c(n-2)为自由度为n-2、显著性水平为1-c的t分布;Sr为残余标准差。
假设寿命N服从对数正态分布,即Y服从正态分布,由极大似然估计法可以求得 Aμ、Aσ、Bμ和 Bσ的值,即
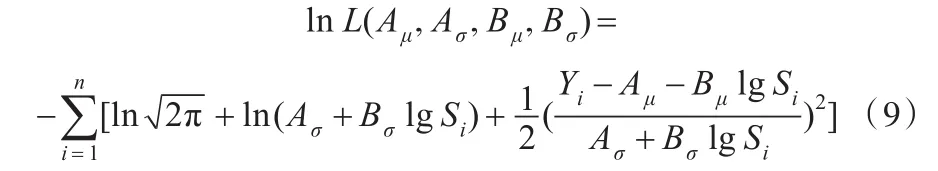
为便于计算,首先使用最小二乘法大致估算Aμ和 Bμ的值,再代入式(9)计算,且最小二乘法的计算依据为
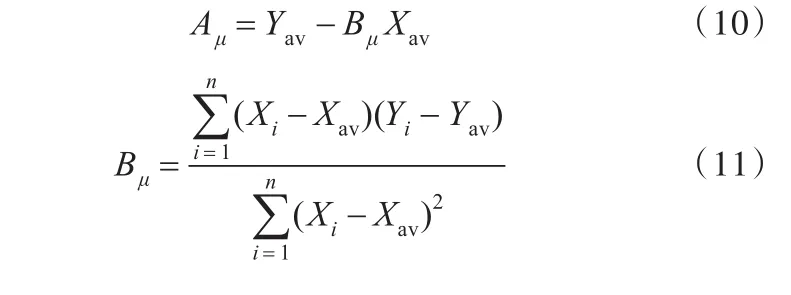
由此求得 Aμ、Aσ、Bμ和 Bσ的值后,即可通过式(5)确定中高段寿命区间曲线。
1.3 ER8材料低温环境下超高寿命区间p-c-S-N曲线外推
外推法广泛运用于p-c-S-N曲线的求取中,以往的外推方法虽能节省大量时间,但精度不佳,对后续的疲劳寿命评价影响很大。CPM方法[8-9]在双对数坐标系中描述p-c-S-N曲线,全寿命区间由两段直线表示,将中高段寿命曲线在转换点NT(NT为材料中高段寿命区间p-c-S-N曲线到超高寿命区间p-c-S-N曲线转换的循环数)处改变斜率进行外推,得到第二段直线,用以表示超高寿命区间,从而获得全寿命区间p-c-S-N曲线:
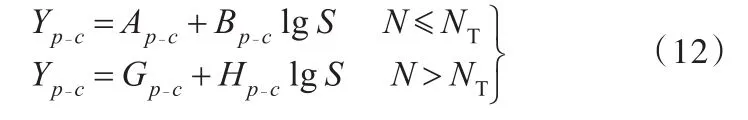
其中,Ap-c、Bp-c的值由式(6)、式(7)计算,Gp-c、Hp-c的值由文献[8]计算。
2 结果与讨论
2.1 ER8材料的低温p-c-S-N曲线
由成组法试验结果,经式(8)~式(11)计算,得到ER8材料-40℃下p-c-S-N曲线的基本参数(见表1)。其中,kT为材料中高段寿命区间p-c-S-N曲线到超高寿命区间p-c-S-N曲线转换对应的转换系数,NT和kT的计算方法见文献[8]。

表1 ER8材料-40℃下p-c-S-N曲线基本参数Tab.1 Basic parameters of p-c-S-N curves of ER8 at-40℃
式(12)中A、B、G、H四个参数的计算结果见表2,由表2结果结合式(12)即可求得ER8材料-40℃下的全寿命区间p-c-S-N曲线。
取c=50%,分别采用AASHO标准、ECCS标准以及CPM方法作ER8材料-40℃的p-S-N图,结果见图3。
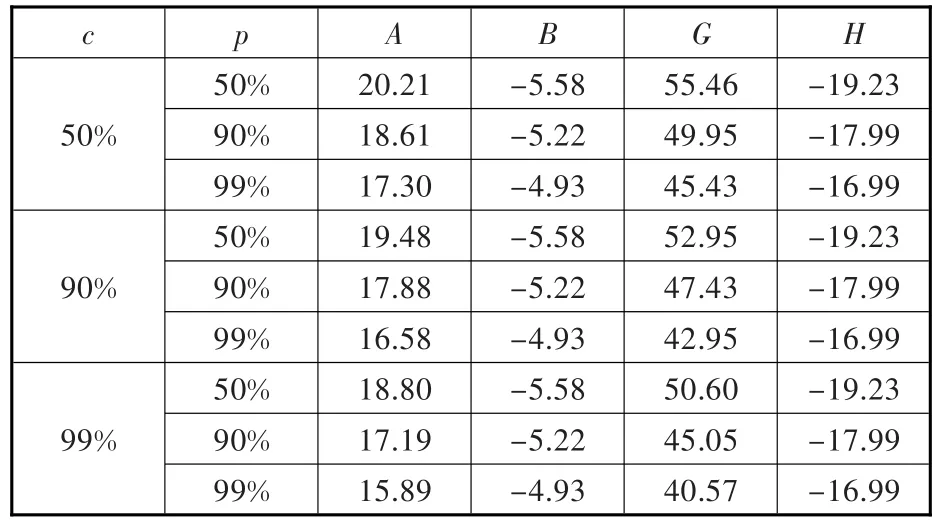
表2 不同p-c水平下ER8材料的曲线参数值Tab.2 Parameters of ER8 p-c-S-N curves at different p-c levels
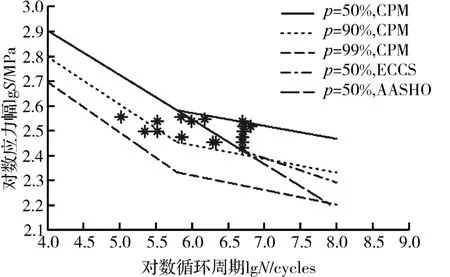
图3 三种不同外推方法下ER8材料的低温p-c-S-N曲线比较(c=50%)Fig.3 Comparison of 3 different extrapolation methods(c=50%)
由图3可知,AASHO以及ECCS方法相比于CPM方法而言过于保守,以p、c皆为50%为例,此时升降法试验所得疲劳极限为343.53 MPa,而AASHO以及ECCS方法外推值为264.81 MPa,显著低于试验值,故若以这两种方法所得曲线为参考进行抗疲劳设计,不能充分发挥出材料的性能,而使用CPM方法外推值为343.48 MPa,与试验值接近,外推效果好。
考虑车轮结构的表面加工系数f和尺寸因素k,对ER8材料的p-c-S-N曲线进行修正,得到车轮危险部位的p-c-S-N曲线,如图4所示,其中,km=0.86,kr=0.034,fm=1,fr=0.03,km、kr、fm和 fr分别为尺寸因素和加工系数的均值和标准差。以此曲线计算车轮低温概率疲劳寿命。
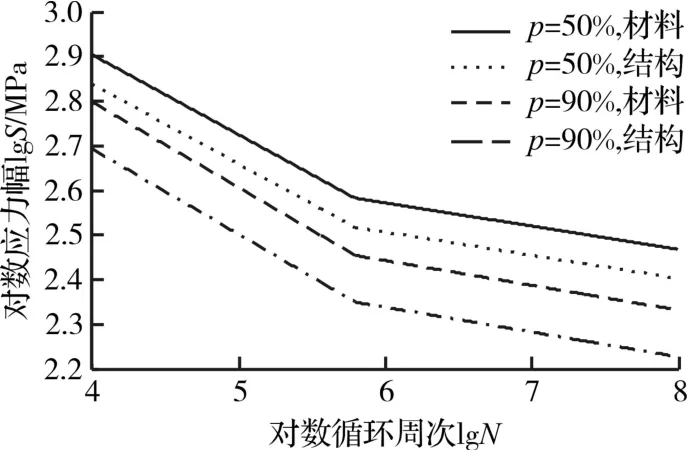
图4 车轮结构p-c-S-N曲线(c=50%)Fig.4 p-c-S-N curves of wheel structure(c=50%)
2.2 车轮的低温概率疲劳寿命
本文以CPM方法所得到的ER8材料全寿命p-c-S-N曲线为依据计算CRH5型动车组车轮概率疲劳寿命。由文献[10-11]知,车轮疲劳失效的典型形式是车轮辋裂,其中车轮踏面表面下1~4 mm的轮辋部分是车轮的危险部位,以此部位的疲劳寿命代表车轮的疲劳寿命是合理的。
通过Simpack软件建立动车组动力学模型,线路模型采用直道加弯道的组合,参考哈大铁路实测数据,直道占比53%,弯道占比47%,仿真得到动车组以200 km/h的速度在典型直道及弯道工况下运行时前转向架动力轮对右车轮的载荷-时间历程,如图5所示。由图5可以看出,在轨道不平顺状况下,车轮垂向力很大。

图5 CRH5车轮垂向力时间历程Fig.5 Vertical force of CRH5 wheel
根据UIC510-5标准进行车轮静强度分析,得到踏面下不同深度的应力水平(见表3)。表3显示踏面下2 mm位置为车轮危险点。
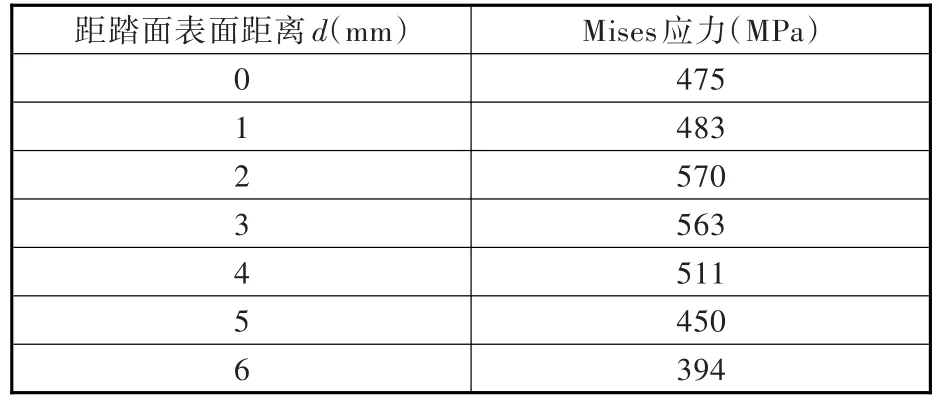
表3 距离车轮踏面表面不同距离的应力水平Tab.3 Stress level with different distance to wheel tread
然后将上述载荷时间历程作为输入使用ABAQUS对车轮进行有限元分析,危险点的应力-时间历程如图6所示。
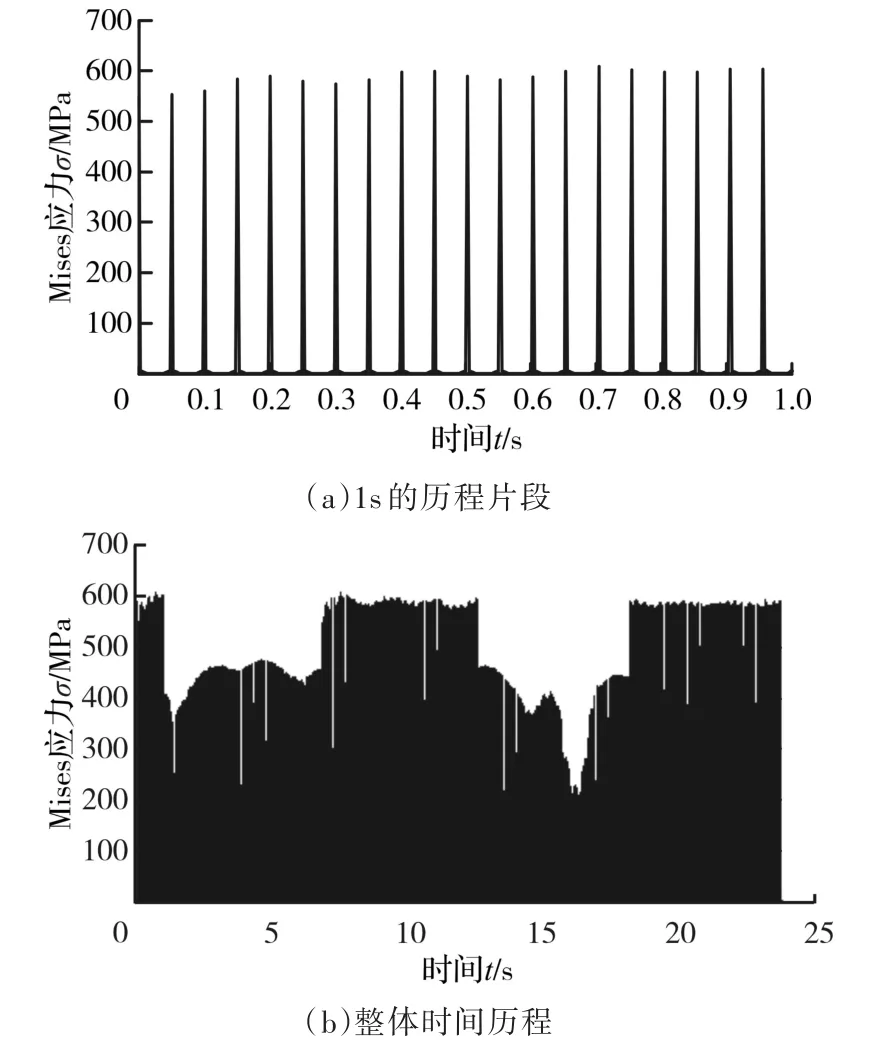
图6 CRH5动车组车轮危险点应力-时间历程Fig.6 Stress-time history of wheel key point of CRH5
图6b为时长1s的危险点应力时间历程片段,由图6b可知,车轮在运行过程中承受了周期性的冲击载荷,这是由车轮的滚动使其与铁轨产生周期性的接触而导致的。由图6可见,轮轨接触区范围很小,当车轮高速滚动时,危险点由接触区外进入接触区域,在极短的时间内通过接触区后离开,造成应力在短时内剧烈地波动,从而产生周期性的冲击载荷,导致出现滚动接触疲劳,这是车轮疲劳失效的根本原因。
通过雨流计数法及平均应力修正法得到的危险点应力谱见表4。
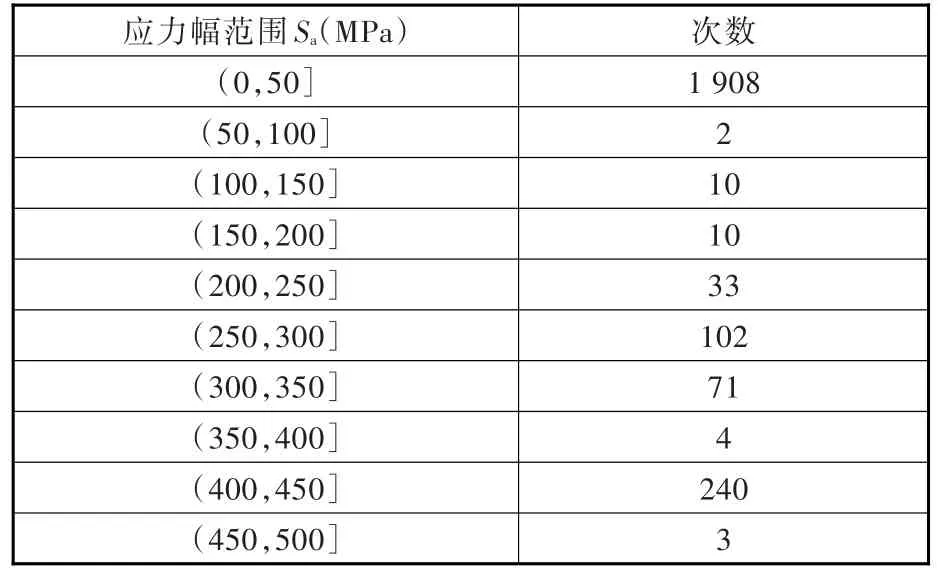
表4 CRH5动车组车轮危险点应力谱Fig.4 Stress spectrum of wheel key point of CRH5
由表4数据结合p-c-S-N曲线并依据Miner线性损伤累积法则,计算车轮的概率疲劳寿命,结果见表5,同时由文献[12]中获得的常温车轮概率疲劳寿命也列于表5中[12]。
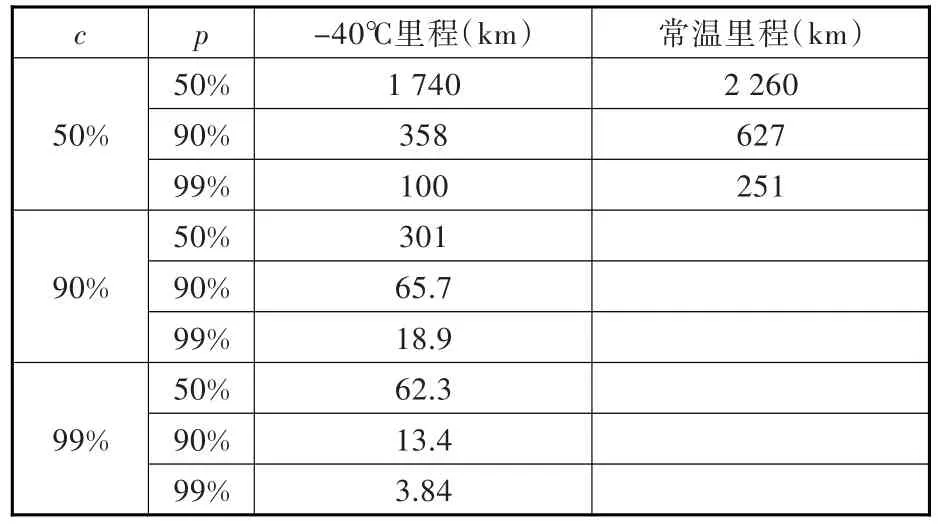
表5 CRH5车轮的概率疲劳寿命Fig.5 Probabilistic fatigue life of CRH5 wheel
由表5中数据可知,c=50%时,随着p值的增大,车轮的寿命无论在常温还是低温下都会迅速地缩短。同时,在p、c皆为50%水平下,车轮在-40℃时的寿命较常温时缩短23%,表明低温环境对于车轮疲劳寿命产生了较大影响。相关研究[13]发现,某些钢材在低温下的S-N曲线较常温时更平缓,二者会发生交叉,导致出现高应力区常温寿命更高、低应力区低温寿命更高的现象。表5中的寿命皆对应于中高应力区间,与这一现象吻合,即ER8钢材在低温下高应力区间的性能不足。
此外,整体的车轮寿命普遍较短,例如c=50%,p=99%时整体的车轮寿命只有100 km,表明在动车组运行过程中,踏面下2 mm处极易萌生裂纹,所以在列车日常检修中,应当对这一区域进行细致检查,及时排除隐患,防止由于裂纹扩展导致车轮断裂造成严重后果。
3 结论
(1)通过试验结合外推法,能够用较短的时间获得较为精确的曲线。AASHO标准以及ECCS标准在外推时过于保守,与试验值存在较大偏差,而使用CPM方法进行外推与试验值基本吻合。
(2)车轮与轨道的滚动接触所导致的周期性冲击载荷是车轮产生疲劳失效的根本原因。车轮的高速转动会使轮轨接触区域不断变化且接触时间极短,踏面任一危险点在进入轮轨接触时应力迅速增大,脱离接触时应力迅速减小,周而复始,从而产生周期性的冲击载荷,使车轮产生疲劳失效。
(3)车轮踏面下2 mm的轮辋部位是车轮的危险部位,在动车运行中易产生疲劳裂纹。踏面下2 mm区域寿命较短,表明这一区域存在裂纹损伤,应在检修中重点关注这一区域,对可能存在的裂纹采取适当的措施。
(4)车轮-40℃下的疲劳寿命较常温下的疲劳寿命出现大幅度的缩短。在相同p、c水平下,车轮低温下的疲劳寿命较常温时出现了大幅度缩短,可以确定低温环境对车轮疲劳寿命存在严重的影响,应在设计制造中采用低温性能更好的材料或者改变车轮踏面类型降低车轮踏面应力水平,从而延长车轮的疲劳寿命。
参考文献:
[1] 卢纯.高速动车组车轮踏滚动接触疲劳的萌生机理研究[D].成都:西南交通大学,2015.
LU Chun.A Study on Rolling Contact Fatigue of High-speed EMU Wheels[D].Chengdu:Southwest Jiaotong University,2015.
[2] PENG D,JONE R,CONSTABLE T,et al.The Tool for Assessing the Damage Tolerance of RailwayWheel under Service Conditions[J].Theoretical and Applied Fracture Mechanics,2012,57:1-13.
[3] 秦大同,谢里阳.疲劳强度与可靠性设计[M].北京:化学工业出版社,2013:8-9.
QIN Datong,XIE Liyang.Fatigue Strength and Reliability Design[M].Beijing:Chemical Industry Press,2013:8-9.
[4] SPRIESTERSBACH D,GRAD P,KERSCHER E.Influence of Different Non-metallic Inclusion Types on the Crack Initiation in High Strength Steels in the VHCF Regime[J].International Journal of Fatigue,2014,64:114-120.
[5] ZHAO Y X.ProbabilisticFatigueS-N Curves Including the Super Long Life Regime of a Railway Axle Steel[J].International Journal of Fatigue,2009,31:1550-1558.
[6] 高镇同.疲劳性能测试[M].北京:国防工业出版社,1980:87-90.GAO Zhentong.Fatigue Test[M].Beijing:National Defence Industry Press,1980:87-90.
[7] ZHAO Y X,YANG B.Probabilistic Measurements of the Fatigue LimitData from a SmallSampling Up-and-down Test Method[J].International Journal of Fatigue,2008,30:2094-2103.
[8] ZHAO Y X.A Fatigue Reliability Analysis Method Including Super Long Life Regime[J].International Journal of Fatigue,2012,35:79-90.
[9] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2008:73-76.
LI Qingyang,WANG Nengchao,YI Dayi.Numerical Analysis[M].Beijing:Tsinghua University Press,2008:73-76.
[10] 张澎湃.动车组车轮疲劳性能数值仿真和评定方法研究[D].北京:中国铁道科学研究院,2014.
ZHANG Pengpai.Research of EMU Wheel's Fatigue Performance Simulation and Assessment Method[D].Beijing:China Academy of Railway Sciences,2014.
[11] 杨柳青.CRH5型动车组轮轨磨损及疲劳性能研究[D].杭州:浙江理工大学,2016.
YANG Liuqing.Research of Wear and Fatigue Life of Wheel of CRH5[D].Hangzhou:Zhejiang Sci-tech University,2016.
[12] 蔡慧.CRH5动车组动力轮对的可靠性分析[D].成都:西南交通大学,2014.
CAI Hui.Reliability Analysis on the Power Wheel-set ofCRH5TypeEMU[D].Chengdu:Southwest Jiaotong University,2014.
[13] 张玉玲,潘际炎.低温对钢材及其构件性能影响研究综述[J].中国铁道科学,2003(24):89-95.
ZHANG Yuling,PAN Jiyan.Study on Performance of Steel and the Components under Low Temperature[J].China Railway Science,2003(24):89-95.
(编辑 王艳丽)
作者简介:杨柳青,男,1990年生,博士研究生。研究方向为机械零部件疲劳可靠性。E-mail:409709426@qq.com。

