粉末高速压制成形件密度影响因素分析
于世伟 周 剑 张 炜 张雪洁 刘 焜
合肥工业大学摩擦学研究所,合肥,230009
0 引言
粉末高速压制技术是在压制压力为600~2 000 MPa,压制速度为2~30 m/s的条件下对粉体进行高能冲击的压制技术,在压制过程中释放的能量能够使粉末瞬时达到致密化和均匀化[1]。目前,国内外学者主要从实验和模拟两方面对粉末高速压制展开研究。WANG等[2]研究了粉末高速压制过程中应力波的传递现象以及应力波对压坯质量的影响。KHAN等[3]研究了冲击力、冲击速度等参数对抗拉抗弯强度以及硬度等力学性能的影响。HAGGBLAD等[4]通过改进实验装置的方式减少了因卸载和加载方式不当导致的密度不均和压坯表面剥落的现象。上述文献侧重于对粉末高速压制实验结果的定性分析研究,对粉末密度及其均匀性量化分析较少。
YANG等[5]利用X射线断层扫描技术,计算出粉末高速压制获得的压坯自上而下7层坯料的平均密度,发现改善模具内壁润滑条件比增大压制压力更能够有效提高压坯密度均匀性,且压坯致密化进程通常发生在压坯下部。TANIGUCHI等[6]先将铁粉分次放入模具内腔进行预压,在较大的压力下将4层压坯压实,而后将4层压坯分别分开,利用该方法研究不同润滑剂对密度沿高度方向分布规律的影响,发现润滑剂用量与密度均匀性的提高呈线性关系,石蜡涂抹于模具内壁时密度均匀性的改善程度要高于硬脂酸锌涂抹于模具内壁时密度均匀性的改善程度。DOREMUS等[7]通过实验的方式将高速压制坯料与普通压制坯料的密度及其分布进行了比较,发现高速压制能够得到密度值较大的压坯且均匀性较好,同时发现边壁润滑条件对压坯密度数值影响不大。
粉末高速压制压坯密度分布不均主要由颗粒间摩擦和颗粒与模具内壁摩擦引起。粉末压制初期,颗粒处于重排阶段,颗粒间摩擦起主导作用;当颗粒间压力增大时,颗粒运动受限,颗粒与模具内壁摩擦起主导作用,且这一阶段对压坯密度的最 终分布起 决定性作 用[8]。王 德广等[9]利用MARC软件对粉末高速压制进行仿真时发现,单位质量能量和高径比等因素对压坯密度分布有不同程度的影响。AN等[10]认为粉末初始松装密度也对密度的分布产生影响。目前,虽然学者们研究了影响粉末高速压制压坯密度的各种因素,但是未进行这些因素对密度大小和均匀性的影响程度的具体定量分析。
本文利用ABAQUS中的Drucker-Prager Cap[11]本构模型,对粉末高速压制过程进行模拟,得到粉末高速压制压坯相对密度分布及不同参数对密度及其均匀性的影响,并利用正交试验手段对密度均匀性各因素的敏感性进行了分析,以期为提高粉末高速压制成形产品的密度和均匀性提供理论指导。
1 有限元模拟
1.1 高速粉末成形过程的有限元模型建立
本文以Distaloy AE铁粉的圆柱压坯为研究对象,模拟研究粉末高速压制过程中压坯相对密度及其分布情况。该粉体的粒度分布情况如图1所示。
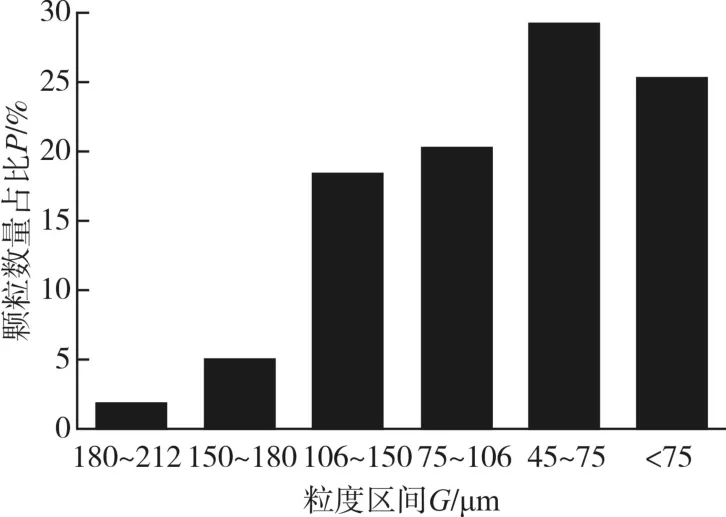
图1 Distaloy AE铁粉粒度分布情况Fig.1 Particle size distribution of Distaloy AE
粉体压制前尺寸由装粉量和初始松装相对密度决定,由于粉末压坯和成形模具的轴对称特征,在非线性有限元软件ABAQUS中建立旋转轴对称模型,图2为高速压制模拟的旋转轴对称模型,该模型的尺寸以实际实验中的高速压机为参照。由于高速压制属于瞬态冲击过程,因此采用ABAQUS中的显式动力学模块(Dynamic Explicit)进行求解,其中重锤质量为50 kg,重锤与上冲头接触的速度由重锤下落高度决定。下冲头与模具之间采用完全固定的约束方式,整个冲压过程的时间为2~4 ms,模具内腔直径设置为16 mm,粉末体网格划分尺寸为0.05 mm,模具网格划分尺寸为0.2 mm。
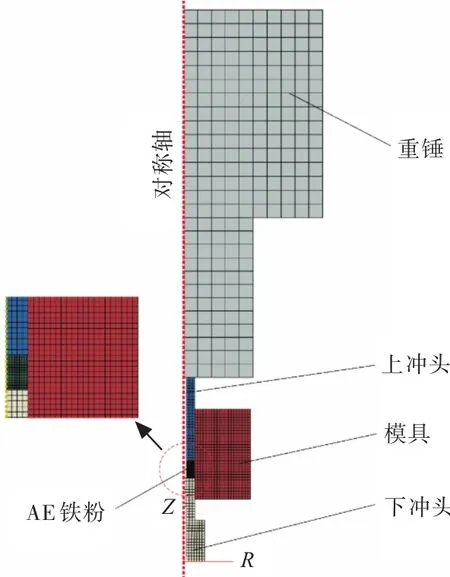
图2 高速粉末成形过程的有限元模型Fig.2 Finite element model of high speed powder forming process
1.2 Drucker-PragerCap材料模型及在ABAQUS中的实现
在对粉末压制进行模拟时,选取合适的连续性材料模型是模拟粉末压制的关键。Druck⁃er-Prager Cap(DPC)模型是在 Drucker-Prager模型的基础上加入了盖帽状屈服面(CAP)[12],它可以有效反映材料因压缩而导致的屈服,最初用于岩土力学领域。相比于其他模型,DPC模型优点在于该模型能够捕捉粉末中的剪切现象[13],因而适用于粉末高速压制的模拟。
DPC模型如图3所示,由三段曲线组成:剪切破坏面曲线、光滑过渡面曲线和盖帽面曲线,各曲线分别由下式定义:

式中,p为等效压应力;q为Misses等效应力;R为盖帽屈服面的曲率;d为内聚力;α为过渡面曲率;β为摩擦角;pa为材料硬化的塑性体积应变参数;pb为压缩屈服平均应力;t为偏应力。

图3 修正DPC模型屈服面Fig.3 Yield surface of modified DPC model
Drucker-Prager Cap模型由参数d、R、β、α和k决定,k为材料参数,用于控制屈服面对中间主应力值的依赖性。由于DPC模型各参数在粉末压制过程中随密度(此处及下文出现的密度均指量纲一化的相对密度)不断变化,因此ZHOU等[14]通过实验的方法以Distaloy AE铁粉为压制对象,对前述参数进行拟合,以密度 ρ为自变量,各参数为因变量,其中α和K分别取0.02和1。此外在模拟中还需加入弹性模量E和泊松比υ,上述参数与密度的关系如表1所示。其中,R1和R2为常数,分别为0.23和0.58;ρc为密度拟合参数。

表1 DPC模型各参数随密度ρ的变化公式Tab.1 The formulas of the parameters in the DPC model vary with the density in compact process
CHTOUROU等[15]在研究塑性体积应变 εV与相对密度的关系时,提出下式:

式中,ρ、ρ0分别为压制过程中不断变化的相对密度和压制前的初始松装相对密度。
本文通过有限元软件ABAQUS提供的二次开发平台,编写基于Fortran语言的用户子程序(VUSDFLD),将每一增量步所得到的各节点的体积应变数值,通过式(4)转化成相对密度值,将相对密度定义为场变量,以不断更新每个增量步中DPC模型各参数的值。
2 结果与讨论
影响密度的参数主要为边壁摩擦因数 μ[2]、高径比 H/D[16]、单位质量能量 E/m[17]和初始松装密度ρ0
[3],其中单位质量能量为冲击能量和装粉量的比值。为探究在粉末高速压制过程中不同参数对压坯密度及均匀性的影响,本文选取上述四个参数作为自变量,密度及其均匀性作为因变量,并在模拟的过程中利用控制变量法,探究某一变量对密度及其均匀性的影响。模拟过程中,参数作为变量时的数值如表2所示。

表2 模拟过程参数变化范围Tab.2 Parameters range in simulation process
2.1 密度分布规律
图4为在边壁摩擦因数为0.4、高径比为1.5、初始松装相对密度为0.4和单位质量能量为50 J/g条件下模拟的密度分布情况。图4a和图4b所示分别为压坯整体密度分布和A、B两点密度随时间的变化情况。图4a中密度分布呈现压坯边缘密度自上而下逐渐变小、中部密度分布较为均匀、粉末密度不均匀主要集中于靠近边壁处的现象。这与黄培云[18]提出的密度分布规律较为吻合。图4b中A、B两点密度随着时间的延长,密度差距逐渐变大,且由于回弹的作用,使得A、B两点的密度在达到最大值后会出现较小的回落现象。
图4c、图4d所示分别为密度沿不同方向和区域的分布情况。从图4c、图4d中可以看到,上下端面的密度值随着径向距离的增大分别呈上升和下降趋势;压坯靠近边壁的密度随着轴向距离的增大而逐渐增大,而内部的密度沿轴向变化不明显。这主要是由于边壁摩擦的存在,使得应力在传递过程中随传递距离的增大而逐渐减小,这就导致越靠近边壁的粉末体,即压坯边缘处,其密度分布越不均匀,而相较之下,压坯内部,即远离边壁区域,其密度分布较为均匀。
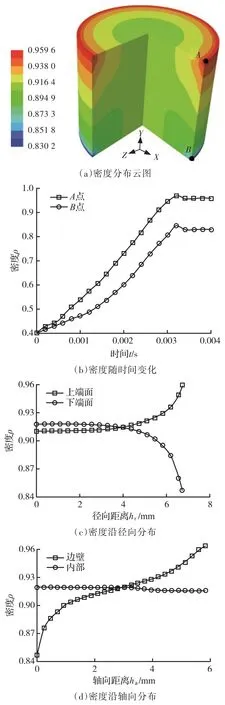
图4 密度分布情况Fig.4 Density distribution
2.2 密度影响因素分析
图5分别为边壁摩擦因数 μ、高径比H/D、单位质量能量E/m和初始松装密度 ρ0对粉末高速压制压坯平均相对密度的影响。模拟结果显示,在各影响因素中,单位质量能量对密度影响最为明显。密度随着单位质量能量的增大呈现先增大,后趋于不变的规律。模拟中,Distaloy AE铁粉单位质量能量的临界值为90 J/g,与文献[17]中钛粉的单位质量能量临界值95 J/g相比较发现略小,单位质量能量的临界值与粉末的种类有关。其他三个因素对密度的影响较小,这主要是由于这三个因素的改变并不能有效增大粉末颗粒的塑性变形,使得压坯整体密度并不能发生较大的改变。因此在实际生产中,应从单位质量能量入手来提高压坯密度,但一味提高高速压制过程中的冲击能量并不能持续提高压坯的密度,应根据不同种类的压制粉末选取合适的单位质量能量。

图5 不同影响因素与密度的关系Fig.5 The relationship between different influencing factors and density
2.3 密度不均匀性影响因素分析
密度均匀性对粉末冶金制件的力学性能影响较大,因此对压坯密度均匀性的研究具有重要意义。图6分别为单位质量能量E/m、高径比H/D、边壁摩擦因数 μ和初始松装相对密度 ρ0对粉末高速压制压坯密度均匀性的影响,其中密度均匀性用密度的标准差ρσ表示,标准差越小意味着密度越均匀。
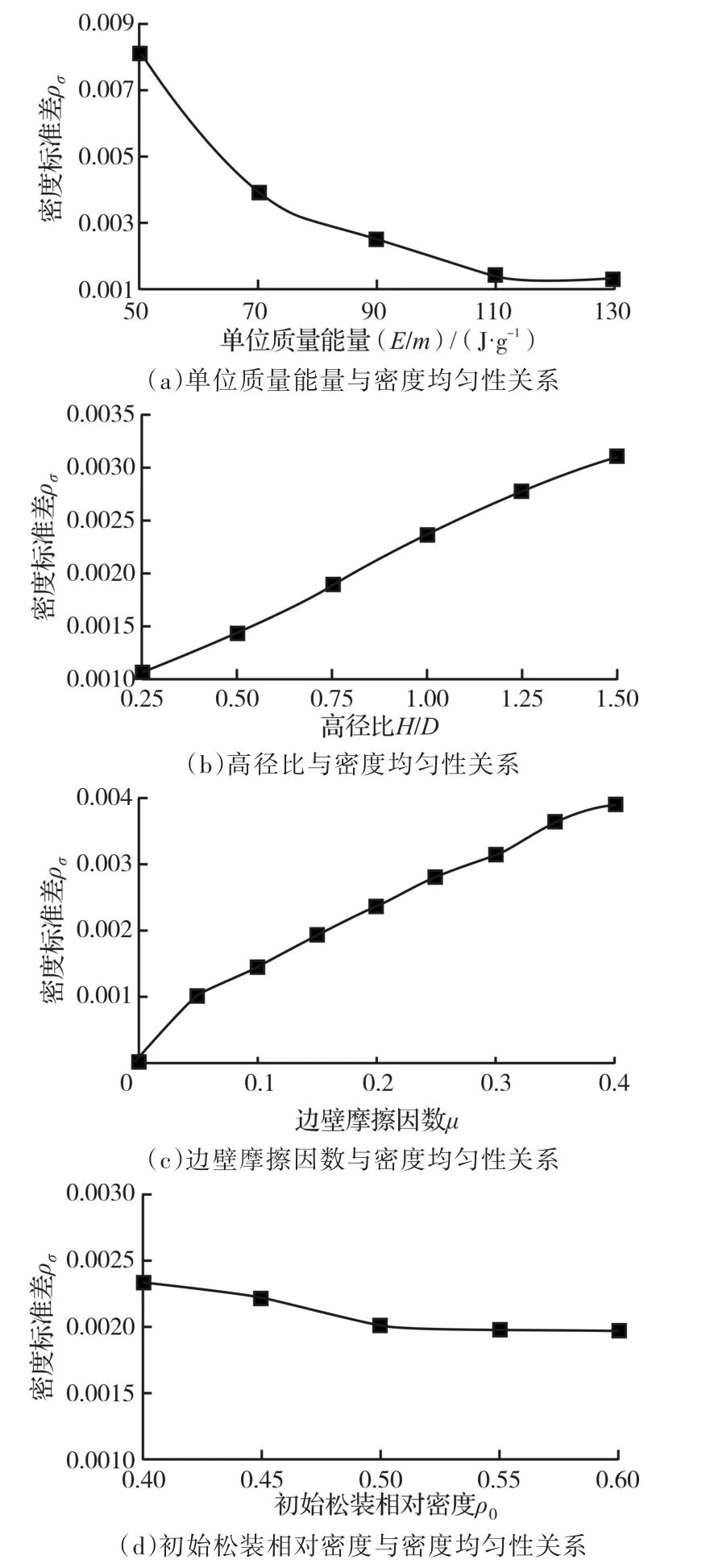
图6 不同影响因素与密度均匀性的关系Fig.6 The relationship between different influencing factors and density uniformity
从图6可以看出,对密度均匀性具有正相关作用的因素为单位质量能量和初始松装相对密度;对密度均匀性具有负相关作用的因素为边壁摩擦因数和高径比。密度标准差随着边壁摩擦因数的增大而出现递增趋势,这主要是由于边壁摩擦因数的增大会增大边壁摩擦力,靠近边壁的粉末体由于摩擦力的增大,其挤压程度的差异变大,使得密度不均匀性加剧;同样,高径比和密度不均匀性也出现类似的变化规律,与边壁摩擦因数不同的是,高径比的增大虽然没有增大摩擦力,但是在相同装粉量的条件下,会增大粉末体与模具内壁接触的侧面积,从而放大了摩擦力对密度均匀性的影响;当单位质量能量增大时,密度不均匀性数值逐渐降低,当其达到110 J/g后,曲线变化趋势趋于平缓,密度不均匀性数值趋近于一定值,结合上文中,当单位质量能量达到90 J/g时,密度不再上升,我们知道,虽然将单位质量能量从90 J/g提升到110 J/g时,密度无法进一步增大,但是其密度均匀性会进一步提高;同样,当初始松装密度达到0.5时,密度不均匀性数值不再下降,因此在高速压制前,适当提高初始松装密度至0.5左右即可达到最佳效果。
2.4 密度大小和分布不均匀性正交试验分析
为了探究各因素对密度均匀性的影响程度,本文采用正交试验的方式对影响程度进行定量分析。选取影响密度均匀性的主要参数为:模具内壁摩擦因数 μ、高径比H/D、单位质量能量E/m和粉末初始松装相对密度ρ0。根据标准正交表,选用L9(34)正交表进行试验安排,得到结果如表3所示,其中为平均相对密度。
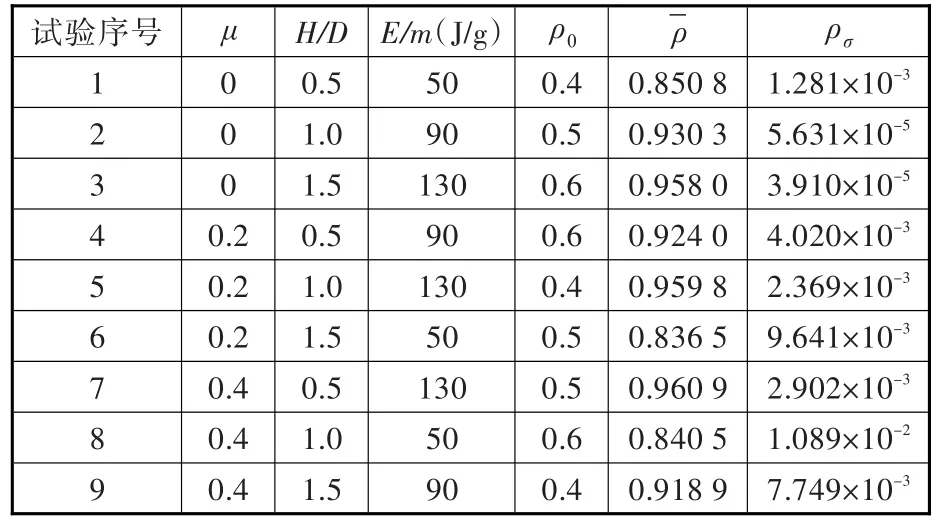
表3 试验安排与结果Tab.3 Test arrangement and results
图7为各影响因子与密度值关系图。对密度影响的主次顺序为单位质量能量、高径比、边壁摩擦因数和初始松装相对密度,但是相比于单位质量能量,其余三个变量对密度值影响十分微弱,因而在实际生产中增加单位质量能量是提高密度的最有效办法。
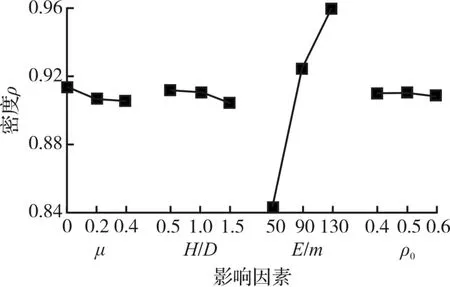
图7 各因素对密度大小影响趋势图Fig.7 The tendency of density influenced by different factor

图8 各因素对密度均匀性影响趋势图Fig.8 The tendency of density uniformity influenced by different factors
图8为各影响因子与密度不均匀性关系图,可以看到,密度均匀性随模具内壁摩擦因数和高径比的增大而降低,随单位质量能量和初始松装相对密度的增大而增大。对密度均匀性影响的主次顺序为边壁摩擦因数、单位质量能量、高径比和初始松装相对密度,其中最优组合为:边壁摩擦因数为0,高径比为0.5,单位质量能量为130 J/g,初始松装相对密度为0.6。其中对密度均匀性影响最大的是模具内壁摩擦因数,因此改善模具内壁润滑条件是保证粉末压制成品密度均匀性的最为关键的手段之一;单位质量能量也对密度均匀性起着较大影响,随着冲击能量的增大,密度均匀性也在不断改善,这也是粉末高速压制技术优于普通压制技术的优点之一。因此在实际生产中,应尽可能改善模具内壁润滑条件,当润滑条件无法进一步改善时,适当提高冲击高度也可进一步提升密度均匀性;在某些工况下,单位质量能量和润滑条件都无法改变时,可以通过改变粉末体的形状因子(高径比)和初始松装相对密度来小幅提高密度均匀性。
3 结论
(1)压坯密度不均匀主要集中于上下端面边缘附近区域,其中上端面边缘处密度最大,下端面边缘处密度最小,边壁摩擦的存在导致压坯靠近边壁处的部分密度不均匀性加剧。
(2)粉末高速压制过程中,单位质量能量是影响密度的主要因素,提高边壁润滑条件、改变高径比、提高初始松装密度并不能有效提高压坯密度;边壁摩擦因数和单位质量能量对密度均匀性影响较大。
(3)密度随着单位质量能量的增大而不断增大,当单位质量能量达到临界值后密度值不再增大;密度均匀性随着边壁摩擦因数或高径比的增大而不断变差,随单位质量能量和初始松装密的增大而不断改善。例如,对于Distaloy AE铁粉,单位质量能量增大到90 J/g以上时,虽然密度无法再增大,但是密度均匀性继续改善。
参考文献:
[1] 周晟宇,尹海清,曲选辉.粉末冶金高速压制技术的研究进展[J].中国材料进展,2010,29(2):45-49.
ZHOU Shengyu,YIN Haiqing,QU Xuanhui.Research Progress of High Speed Pressing Technology for Pow⁃der Metallurgy[J].Materials China,2010,29(2):45-49.
[2] WANG Jianzhong,QU Xuanhui,YIN Haiqing,et al.High Velocity Compaction of Ferrous Powder[J].Chi⁃nese Journal of Materials Research,2008,192(1):131-136.
[3] KHAN D F,YIN H Q,MATIULLAH M,et al.Analysis of Density and Mechanical Properties of Iron Powder with Upper Relaxation Assist through High Velocity Compaction[J].Materials Science Forum,2013,749 :41-46.
[4] HAGGBLAD H A,HOCKAUF M,ERIKSSON M,et al.Simulation of High Velocity Compaction of Powder in a Rubber Mould with Characterization of Silicone Rubber and Titanium Powder Using a Modified Split Hopkinson Set-up[J].Powder Technology,2005,154(1):33-42.
[5] YANG S D,ZHANG R J,QU X H.X-ray Tomography Analysis of Aluminum Alloy Powder Compaction[J].Rare Metals,2015,7:1-7.
[6] TANIGUCHI Y,DOHDA K,WANG Z.Effect of Lubri⁃cation on the Improvement of Uniformity in Uniaxial Powder Compaction[J].JSME International Journal,2005,48(4):393-398.
[7] DOREMUS P,GUENNEC Y L,IMBAULT D,et al.High-velocity Compaction and Conventional Compac⁃tion of Metallic Powders:Comparison of Process Pa⁃rameters and Green Compact Properties[J].Archive Proceedings of the Institution of Mecha.,2010,1(E3):1-9.
[8] MICHRAFY A,DODDS J A,KADIRI M S.Wall Fric⁃tion in the Compaction of Pharmaceutical Powders:Measurement and Effect on the Density Distribution[J].Powder Technology,2004,148(1):53-55.
[9] 王德广,吴玉程,焦明华,等.不同压制工艺对粉末冶金制品性能影响的有限元模拟[J].机械工程学报,2008,44(1):205-211.
WANG Deguang,WU Yucheng,JIAO Minghua,et al.Finite Element Simulation about the Effect of Different Pressing Processes on the Performance of Powder Met⁃allurgy Products[J].Chinese Journal of Mechanical Engineering,2008,44(1):205-211.
[10] AN Xi,ZHANG Y,ZHANG Y,et al.Finite Element Modeling on the Compaction of Copper Powder under Different Conditions[J].Metallurgical and Materials Transactions A,2015,46(8):3744-3752.
[11] DRUCKER D C,GIBSON R E,HENKEL D J.Soil Mechanics and Work-hardening Theories of Plasticity[J].Transactions American Society of Civil Engi⁃neers,1957,122:338-346.
[12] BREWIN P R,COUBE O,DOREMUS P.Modelling of Powder Die Compaction[M].London:Spring⁃er-Verlag,1998.
[13] 费康,张建伟.Abaqus在岩土工程中的应用[M].北京:中国水利水电出版社,2013:18-24.FEI Kang,ZHANG Jianwei.Application of Abaqus in Geotechnical Engineering[M].Beijing:China Water&Power Press,2013:18-24.
[14] ZHOU Rui,ZHANG Lianhong,BAI Yan,et al.Nu⁃merical Simulation of Residual Stress Field in Green PowerMetallurgyCompactsbyModified Druck⁃er-Prager Cap Model[J].Transactions of Nonferrous Metals Society of China,2013,23(8):2374-2382.
[15] CHTOUROU H,GAKWAYA A,GUILLOT M.Model⁃ing of the Metal Powder Compaction Process Using the Cap Model.PartⅠ:Experimental Material Char⁃acterization and Validation[J].International Journal of Solids and Structures,2002,39(4):1059-1075.
[16] 郑洲顺,徐丹,雷湘媛,等.粉末高速压制成形密度分布的数值模拟及影响因素分析[J].材料工程,2012(7):10-14.
ZHENG Zhoushun,XU Dan,LEI Xiangyuan,et al.Numerical Simulation of Density Distribution and Analysis of Influencing Factors in Powder High Ve⁃locity Compaction[J].Journal of Materials Engineer⁃ing,2012(7):10-14.
[17] 闫志巧,陈峰,蔡一湘,等.Ti粉的高速压制成形及表征[J].金属学报,2010,46(2):227-232.
YAN Zhiqiao,CHEN Feng,CAI Yixiang,et al.High Velocity Compaction and Characterization of Ti Pow⁃der[J].Acta Metallurgica Sinica,2010,46(2):227-232.
[18] 黄培云.粉末冶金原理[M].北京:冶金工业出版社,1997.
HUANG Peiyun.Principle of Powder Metallurgy[M].Beijing:Metallurgical Industry Press,1997.
(编辑 王艳丽)
作者简介:于世伟,男,1991年生,硕士研究生。研究方向为数字化设计及现代设计理论。E-mail:hfutysw@mail.hfut.edu.cn。刘 焜(通信作者),男,1963年生,教授、博士研究生导师。研究方向为先进制造技术,机电系统微观尺寸数字化设计、表面摩擦学。发表论文180余篇。E-mail:liukun@hfut.edu.cn。

