环形薄壁类粉末冶金零件压坯残余应力分析

周 蕊，谢 东，李璐璐，张建国

(1.中国民航大学航空工程学院，天津300300; 2.天津科技大学机械工程学院，天津300222)

环形薄壁类粉末冶金零件压坯残余应力分析

周 蕊1，谢 东2，李璐璐2，张建国2

(1.中国民航大学航空工程学院，天津300300; 2.天津科技大学机械工程学院，天津300222)

针对环形薄壁类粉末冶金零件压坯的残余应力进行分析，采用修正的Drucker-Prager Cap弹塑性本构模型对金属粉末压坯压制、卸载和脱模过程进行数值模拟，同时考虑不同零件压坯几何参数(高径比和厚径比)以及压制工艺条件(摩擦条件和脱模角度)对压坯内残余应力的影响.研究结果表明，压坯脱模后的残余应力分布规律是压坯侧表面出现明显的压应力层，内部为拉应力区域，且越靠近压坯中心值越小.随着高径比和厚径比的增加，其残余应力逐渐减小；随着摩擦系数的增加，压坯表面的轴向残余压应力不断增大且压坯内部的拉应力也不断加大；适当增加脱模角度有利于压坯内应力释放而减小残余应力.通过正交模拟试验及方差分析可知，厚径比和脱模角度对金属粉末成形脱模后压坯残余应力影响更为显著.

残余应力；修正的Drucker-Prager Cap模型；粉末冶金；环形薄壁零件

高性能铁基粉末冶金零件有着广泛的应用前途，已普遍用于传动装置、发动机、通用机械和工具等产品.而压坯内残余应力的存在会导致其强度降低，进而在夹持运送、烧结以及后续加工过程中产生变形或引发裂纹[1].因此，对压坯残余应力的研究有助于改善分层裂纹等缺陷，提高粉末冶金制品的力学性能.

关于残余应力的测试方法有很多种[2-3]，由于粉末压坯在未经烧结之前强度较低，更适合采用无损测量的方法.Ericsson[4]采用X射线衍射实验对不同压制力成形的矩形压坯表面残余应力进行测试分析；Schneider[5]用中子衍射实验测试同步器轮毂零件压坯内残余应力值的分布规律；曲牡等人[6]利用自行设计的传感器研究常温成形卸载后压坯内的应力分布.上述无损测量的方法只能对有限点进行测试，若要快速预测压坯内各点的残余应力分布情况，还需借助数值模拟计算.然而，粉末成形过程数值模拟大多对密度分布进行预测分析，对压坯卸载脱模后的应力分布分析较少.Redanz[7]对一种杯型压坯成形卸载后的应力进行分析，用于讨论多种压制方案的合理性；Jonsen[8]则采用DiMaggio-Sandler本构模型完成矩形压坯的残余应力数值模拟，并用Ericsson的X衍射实验数据进行了验证.

本文以环形薄壁类粉末冶金零件压坯为研究对象，采用修正的Drucker-Prager Cap弹塑性本构模型[9]模拟Distaloy AE金属粉末压制成形过程，同时考虑压坯不同几何参数和压制工艺对其残余应力的影响，并对不同影响因素进行方差分析.

1 修正Drucker-Prager Cap模型的应用

材料本构模型是金属粉末成形数值模拟中最为关键的因素，本文采用密度相关的修正Drucker-Prager Cap模型模拟金属粉末成形脱模后的残余应力.其屈服面主要由三部分组成，分别为剪切破坏面Fs、光滑帽子面Fc以及光滑过渡面Ft，如图1所示，表达式如公式(1)(2)(3)所示：

图1 修正的Drucker-Prager Cap模型在p-t空间中的屈服面Fig.1 Yield surface of the modified Drucker-Prager Cap model in p-t plane

(1)

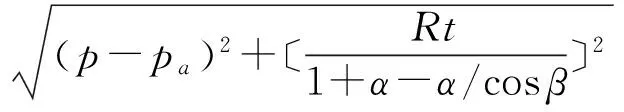
(2)

(3)

由于金属粉末的材料性能随相对密度而变化，因此用修正的Drucker-Prager Cap模型表征其塑性材料属性时，除参数α为常数外，其余参数β,d,Pa,R,Pb均为相对密度ρ相关的函数，并且弹性参数,即弹性模量E和泊松比υ也是相对密度相关的变量，其中参数β,d可通过巴西圆盘实验和单轴压缩实验确定，对于参数R可通过三轴试验确定，同时再结合模压试验确定参数pa,pb，表1给出了一种含合金成分的水雾化铁粉Distaloy AE的材料模型参数[9]，其松装密度为3.08 g/cm3，初始相对密度ρ为0.4.

表1 材料模型参数的函数表达式

注： ρ为相对密度

2 环形薄壁压坯残余应力数值模拟

将环形薄壁零件压坯的几何参数进行参数化处理，当内径D0=22mm，外径D=30mm时，高径比H/D分别为0.4、0.6和0.8时，初始松装高度H0和最终压坯高度H变化情况如表2所示.当初始松装高度H0=26.5mm，最终压坯高度H=12mm时，厚径比T/D分别为0.2、0.3和0.4时，则环形薄壁压坯内外径变化情况如表3所示.当模壁润滑效果不同时，摩擦因数μ取值0.05～0.15.同时考虑阴模脱模角的变化，其示意图如图2所示，参数变化如表4所示.

利用轴对称单元进行数值计算，其示意图如图3所示，其中阴模和芯棒采用线弹体，上下模冲为刚性材料.为更加准确地模拟压坯残余应力，采用X射线衍射实验对圆柱压坯表面残余应力的模拟值进行验证[9]，如图4所示，最终确定粉末体单元靠近阴模和芯棒的最小网格尺寸为0.06mm.对于轴对称边界条件，所有r=0mm的节点沿r方向的位移被约束.采用双向压制且向下脱模的方式，压制过程中的摩擦行为采用库伦摩擦模型.

表2 初始松装高度和最终压坯高度变化情况

表3 内外直径变化情况

表4 脱模角变化情况

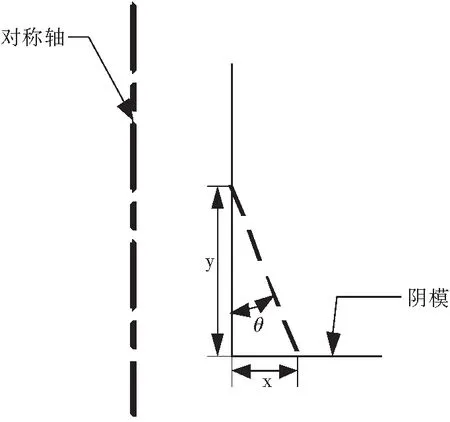
图2 阴模脱模角示意图 Fig.2 Illustration of die taper

图3 压坯成形过程的有限元模型示意图 Fig.3 Finite element model of the compact forming process

图4 X射线衍射实验验证 Fig.4 X diffraction experiment validation (a)—X射线衍谢实验； (b)—网格模型取值

3 数值模拟结果分析

当压坯高径比H/D=0.4，厚径比T/D=0.1， 摩擦系数μ=0.15， 脱模角θ=0(°)时，环形薄壁金属粉末压坯在脱模后沿径向、轴向以及剪切方向残余应力的分布状态如图5所示.金属粉末在压制过程中，由于压制力不能均匀地全部传递，压坯内部承受的应力分布不同，密度分布呈现梯度变化，致使当压力卸载脱模后压坯内部产生残余应力，其分布规律应为内部是拉应力，外部是压应力.图5中，轴向残余应力分布规律最为明显，残余压应力主要集中在靠近模壁一侧外表面，且压坯表面以下约0.2mm出现拉应力层，这种夹层正是造成压坯在脱模过程中出现分层裂纹的原因.而径向和剪切方向的残余应力分布规律相对于轴向残余应力分布对压坯内出现分层裂纹的影响较小，故以下主要对环形薄壁压坯轴向残余应力影响因素进行分析.

图5 压坯径向、轴向以及剪切方向的残余应力分布状态Fig.5 The residual stress distribution in the radial, axial and shear directions of the compact

3.1高径比对环形薄壁金属粉末压坯残余应力的影响

当摩擦系数μ=0.15，厚径比T/D=0.1，脱模角θ=0°，高径比分别为0.4、0.6和0.8时，金属粉末压坯轴向残余应力的分布情况如图6所示.模拟结果表明，在厚径比，摩擦系数以及脱模角一定的情况下，随着高径比的增加，压坯内部的拉应力逐渐减小.压坯侧表面沿轴向各节点残余应力分布曲线如图7所示，其坐标原点为压坯侧表面最下边节点.由图可知，压坯侧表面不是随着高径比的增加而减小，当高径比为0.6时，压坯侧表面的轴向残余压应力最小.这是由于随着高径比的不断增加，压坯的相对密度分布更加不均匀，压坯内部承受的应力分布不同，高径比过大导致压坯侧表面残余应力增大.

图6 不同高径比的压坯轴向残余应力分布情况Fig.6 Axial residual stress distribution of the green compact with different aspect ratio

3.2厚径比对环形薄壁金属粉末压坯残余应力的影响

当摩擦系数μ=0.15，高径比H/D=0.4，脱模角θ=0°，厚径比T/D分别为0.1、0.3和0.4时，压坯轴向残余应力的分布情况如图8所示.模拟结果表明，在高径比，摩擦系数以及脱模角一定的情况下，随着厚径比的增加，压坯内部的拉应力也逐渐减小.压坯侧表面沿轴向各节点残余应力分布曲线如图9所示，最大轴向残余应力基本分布在压坯高度的中间部位，且随着厚径比的增加压坯侧表面的轴向残余应力逐渐减小.

3.3润滑条件对环形薄壁金属粉末压坯残余应力的影响

为研究粉末体与阴模之间的摩擦对残余应力的影响，模型中粉末体与阴模的接触边界设置不同的摩擦系数.当高径比，H/D=0.4，厚径比T/D=0.1，脱模角θ=0°，摩擦系数μ分别为0.05和0.15时，压坯轴向残余应力的分布情况如图10所示.模拟结果表明，压坯内部的拉应力随摩擦系数的增加而增大.压坯侧表面沿轴向各节点残余应力分布曲线如图11所示，压坯侧表面的轴向残余应力随着摩擦系数的增大也不断增加.

图7 不同高径比的压坯侧表面轴向残余应力分布曲线Fig.7 Axial residual stress distribution curves on the side surface of the compact with different aspect ratio

图8 不同厚径比的压坯轴向残余应力分布情况Fig.8 Axial residual stress distribution of the compact with different ratio of thickness to diameters

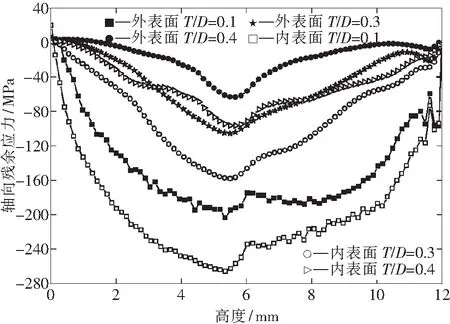
图9 不同厚径比的压坯侧表面轴向残余应力分布曲线Fig.9 Axial residual stress distribution on the side surface of the compact with different ratio of thickness to diameter

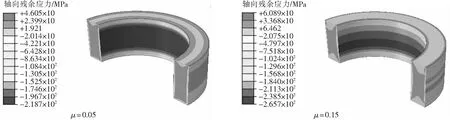
图10 不同摩擦系数的压坯轴向残余应力分布情况Fig.10 Axial residual stress distribution of the compact with different friction coefficients

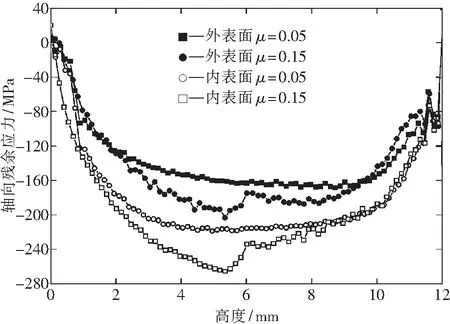
图11 不同摩擦系数的压坯侧表面轴向残余应力分布曲线Fig.11 Axial residual stress distribution on the side surface of the compact with different friction coefficients

3.4脱模角对环形薄壁金属粉末压坯残余应力的影响

当高径比H/D=0.4，厚径比T/D=0.3，摩擦系数μ=0.15，脱模角度按照表4进行设置，压坯轴向残余应力的分布情况如图12所示.模拟结果表明，压坯内部的拉应力有所增加，但增加的幅度不大.压坯侧表面沿轴向各节点残余应力分布曲线如图13所示，压坯侧表面轴向残余应力并不是随着脱模角度的增加而逐渐减小的.当没有脱模角时，压坯的轴向残余应力最大；当脱模角为0.22°时，粉末压坯轴向残余应力最小，适当的脱模角度使粉末压坯在模腔中逐渐释放应力；当脱模角度为0.44°时，压坯侧表面的轴向残余应力反而有所增大.

图12 不同脱模角的压坯轴向残余应力分布情况Fig.12 Axial residual stress distribution of the compact with different die taper

图13 不同脱模角的压坯侧表面轴向残余应力分布曲线Fig.13 Axial residual stress distribution on the side surface of the compact with different die taper

3.5环形薄壁金属粉末压坯残余应力的多因素影响分析

为进一步分析各因素对压坯残余应力影响的显著性，制定了四因素三水平L9(34)正交模拟试验表，如表5所示，并把压坯内部最大拉应力作为评价指标.正交试验的数据处理方法采用直观法，即计算各个因素水平的平均值，如图14所示.可以看出，随着高径比和厚径比的增大，压坯内部的最大拉应力逐渐减小；随着摩擦系数的增加压坯内部的最大拉应力逐渐增大，但变化的幅度较小；当脱模角为0.22°时，压坯内部最大拉应力最小不易产生分层裂纹.通过方差分析P值可知，因素B和因素D对压坯的残余应力影响更为显著.

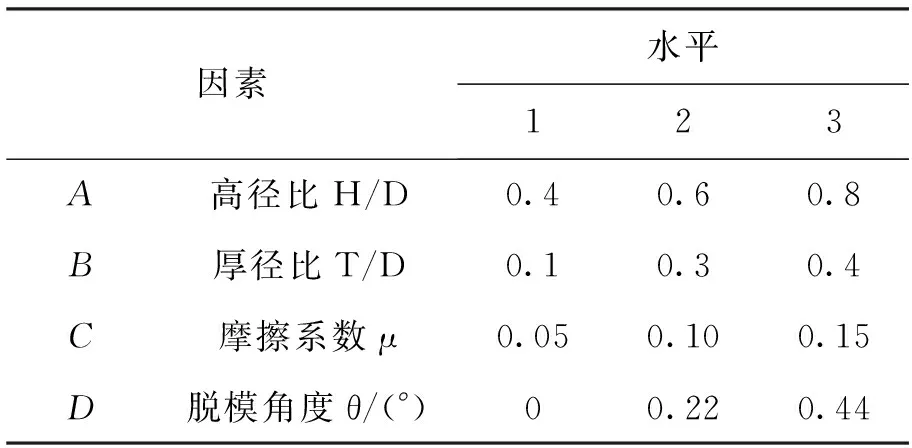
表5 压坯残余应力模拟试验因素水平表

图14 因素水平与评价指标的关系Fig.14 Relationship between factor level and evaluation index

4 结 论

(1)采用修正的Drucker-PragerCap材料模型对合金铁基粉末DistaloyAE的压制、卸载和脱模过程进行数值模拟，研究不同几何参数(高径比H/D、厚径比T/D)和压制工艺(摩擦系数μ、脱模角度θ)对压坯残余应力的影响.研究结果显示，其整体分布规律基本一致，其中轴向残余应力分布特点最为明显，靠近模壁一侧外表面为压应力层，内部为拉应力区域，这种夹层分布规律很好地解释了压坯在脱模过程中出现分层裂纹的原因.

(2)随着压坯高径比H/D和厚径比T/D的增加，压坯内部的拉应力均逐渐减小；摩擦系数μ从0.05增大到0.15，压坯侧表面的轴向残余压应力不断加大，并且压坯内部的拉应力也不断加大；适当增加脱模角有利于压坯内应力的释放，当脱模角θ为0.22°时，压坯残余应力为最小，但继续增大脱模角度，压坯残余应力反而会增加.

(3)通过正交模拟试验与方差分析可知，高径比H/D、厚径比T/D、摩擦系数μ以及脱模角θ对压坯残余应力的影响基本在同一水平，但厚径比 T/D和脱模角θ对压坯残余应力影响更为显著.因此，在实际生产中，需要综合考虑压制成形工艺以及零件结构设计的合理性，以避免出现脱模裂纹，同时将压坯残余应力对后续工序的影响降到最低.

[1]Wenman M R, Price A J, Steuwer A,etal. Modelling and experimental characterization of a residual stress field in a ferritic compact tension specimen[J]. International Journal of Pressure Vessels and Piping, 2009, 86: 830-837.

[2]蒋刚, 谭明华, 王伟明, 等. 残余应力测量方法的研究现状[J]. 机床与液压, 2007, 35(6): 213-220. (Jiang Gang, Tan Minghua, Wang Mingwei,etal. Present research status of measuring residual stress [J]. Machine Tool and Hydraulics, 2007, 35(6): 213-220.)

[3]陈会丽, 钟毅, 王华昆, 等. 残余应力测试方法的研究进展[J]. 云南冶金, 2005, 34(3): 52-54. (Chen Huili, Zhong Yi, Wang Huakun,etal. Research progress of the method for residual stress measurement [J]. Yunnan Metallurgy, 2005, 35(3): 52-54.)

[4]Ericsson T, Larsson C, Peng R L. Studies of residual stress, microcracks, hardness and microstructure of cold compacted metallic green bodies [C]//Engelska M A. Material Research Society Symposium Proceedings. Boston: ASM International, 2003: 53-64.

[5]Schneider L C R, Hainsworth S V, Cocks A C F,etal. Neutron diffraction measurements of residual stress in a powder metallurgy component [J]. Scripta Masterialia, 2005, 52: 917-921.

[6]曲牡, 宫照坤, 陈金涛, 等. 粉末材料常温压制成型残余应力分布研究[J]. 大连理工大学学报, 2000, 40(6): 714-717. (Qu Du, Gong Zhaokun, Chen Jintao,etal. Study on residual stress distribution of powder material at room temperature compression [J]. Journal of Dalian University of Technology, 2000, 40(6): 714-717.)

[7]Redanz P. A Study of stresses in powder compacted components during and after ejection [J]. International Journal of Solids and Structures, 2001, 38: 759-775.

[8]Jonsenp, Haggblab H K. Modelling and numerical investigation of the residual stress in a green metal powder body [J]. Powder Technology, 2005, 155: 196-208.

[9]Zhou Rui, Zhang Lianhong, He Baiyan,etal. Numerical simulation of residual stress field in green power metallurgy compacts by modified Drucker-Prager Cap model[J]. Trans Nonfereous Met Soc China, 2013, 23(8): 2374-2382.

Analysis of residual stress in green compact of circular thin-wall powder metallurgy parts

Zhou Rui1, Xie Dong2, Li Lulu2, Zhang Jianguo2

(1.School of Aeronautical Engineering, Civil Aviation University of China, Tianjin 300300, China；2 School of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China)

Esidual stress of the compacted circular thin-walled powder metallurgy parts was analyzed, and the modified Drucker-Prager Cap model was used to simulate the pressing, unloading, and stripping process of the metal powder compact. Influences of the geometrical parameters (aspect ratio and ratio of thickness to diameter) of the green compact and pressing conditions (friction conditions and die taper) on the residual stress in the green compact were investigated. The results showed that the residual stress after crust stripping has a significant compressive stress layer on the side of the green compact. The inside of the green compact there is a tensile stress region, and the value is smallest in the center of the compact. With increase of the ratios of height to diameter and thickness to diameter, the residual stress decreases; With increase of the friction coefficient, the axial residual compressive stress of the green compact surface increases and the tensile stress inside the green compact also increased; An appropriate increase in the die taper is beneficial to release the stress in the green compact and reduce the residual stress. Through the orthogonal simulation test and the analysis of variance, it was found that the ratio of thickness to diameter and the die taper have a more significant effect on the residual stress of the green compact after forming and stripping the metal powder.

residual stress; the modified drucker-prager cap model; powder matellurgy; circular thin-walled parts

10.14186/j.cnki.1671-6620.2017.03.012

TF 124.31

：A

：1671-6620(2017)03-0218-07