基于高增益观测器的半潜式海洋钻井平台动力定位系统鲁棒滑模控制器设计研究

，， ，

(中国石油大学(华东) 化学工程学院，山东 青岛 266580)

对于深海石油天然气资源的开采，海洋钻井平台是其主要设施，对于早期的海洋钻井平台大多使用锚泊定位方式，一般只适合应用于1 000 m内的水深。当在水深过大的深海作业时，不仅经济性差，而且结构长度及质量过大，会导致海洋平台产生比较大的水平偏航，定位已不再满足工程应用的需要，传统定位技术已无法适用于深海油气开采。动力定位(dynamic position，DP)技术[1-4]应运而生，依靠海洋平台的自身动力即推进器系统，在深水区域进行钻井开采作业是必要选择。控制或中控系统是动力定位系统的关键核心机构，其性能优劣将直接影响着海洋平台的定位性能好坏和稳定性高低，同时又决定着能源消耗的多少。由于在大多数情况下海上钻井平台的速度难以测量。根据噪声污染的位置和航向信号设计状态观测器估计速度信号具有较大的工程实际意义。研究基于状态观测器的闭环控制器设计是海洋平台动力定位控制中的关键问题。

20世纪60年代初，诸多学者设计了带有低通滤波器的传统PID控制器，用以抵消环境因素的干扰。迄今为止，PID控制器+滤波器仍旧是DP控制系统的主要方法。Fung等[5]针对DP控制问题设计了一种自调谐卡尔曼滤波器。Sørensen等[6]研究并拓展到基于模型的控制器设计方法，能够实现定点和轨迹跟踪控制。Tannuri等[7]研究了滑模控制技术在浮式生产储油卸油装置(floating production storage and offloading,FPSO)转台停泊动力定位领域的应用问题。Leira等[8]研究了基于可靠性的浮动船舶DP控制算法问题。Tannuri等[9]提出了一种船舶自适应控制策略，能够实现控制器增益的在线校正，进而可以保证整个操作期间的稳定性能。Tannuri等[10]通过将滑模控制应用在船舶DP系统中的真实实验分析，验证了滑模控制在动力定位系统中应用的有效性和优越性。

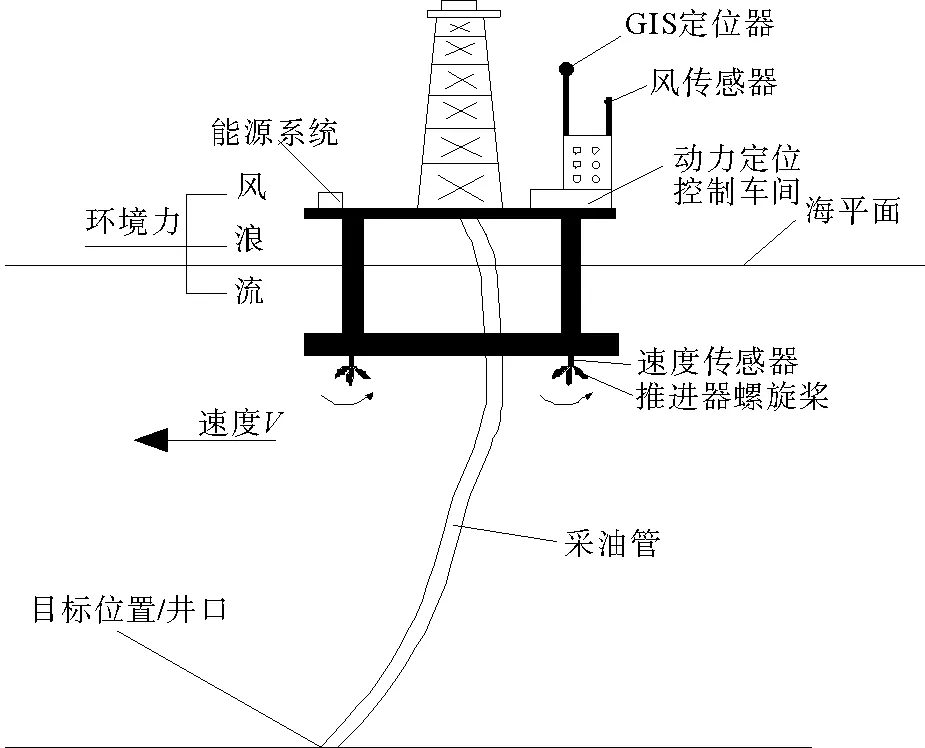
图1 半潜式海洋钻井平台动力定位系统工作过程图Fig.1 The diagram of dynamic positioning system on semi-submersible drilling platform

高增益观测器[11]能够根据平台的位置信号估计其速度信号。滑模变结构控制具有对系统的参数摄动和外部干扰的不变性，能够克服高、低频干扰。因此，本研究提出了一种基于高增益观测器的半潜式海洋平台动力定位系统鲁棒滑模控制器[12-13]的设计方法。充分考虑了外部环境因素如风、浪、流等干扰及内部测量噪声的影响，首先设计高增益观测器对速度信号进行状态估计，得到速度信号。进而利用测量得到的位置信号和估计得到的速度信号进行鲁棒滑模控制器的设计。

1 问题描述

如图1所示，半潜式海洋钻井平台的动力定位系统工作过程的原理如下：

1) 整个海洋平台供能系统由能源系统提供。

2) 中央控制器在动力定位控制车间之中。

3) 目标位置/井口是提前输入的位置信号，通过地理信息系统(geographic information system，GIS)定位器将海洋平台的实时位置信号输入到中央控制器中；另外，推进器螺旋桨的速度信号将通过速度传感器传入到中央控制器中。

4) 中央控制器根据反馈的两个信号(位置信号和速度信号)作出反应，计算出使海洋平台到达目标位置所需的给各个推进器的动力分配，并将该信号传到执行器即推进器的螺旋桨中。

5) 重复过程3)～4)，不断地进行信号反馈与调整，最终保证海洋平台到达目标区域。

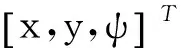
图2 平台地球坐标系和平台坐标系Fig.2 Inertial coordinate system & body fixed coordinate system of platform

(1a)

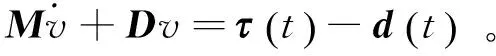
(1b)

其中Jψ为雅可比矩阵。M,D∈R3×3分别代表惯性矩阵和线性阻尼矩阵。τ∈R3×1代表纵荡、横荡方向的控制力及艏摇方向的控制力矩。d∈R3×1代表风、浪、流干扰及未建模动力学特性。

假设d有界，满足:

dt0。

(2)

雅可比矩阵可以用于描述运动方程，即：

(3)

(4)

(5)

Jψ对于所有ψ均是非奇异的。

(6)

由式(1a)，v可以表示为：

(7)

对式(7)进行求导，可得：

(8)

联立式(1b)和(8)，整理得到：

(9)

令

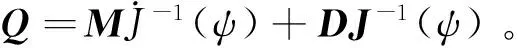
(10)

式(9)可以简化为：

(11)

2 高增益观测器及鲁棒滑模控制器设计

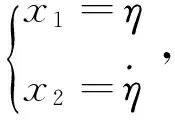
(12)

根据文献[14]设计如下高增益观测器：

(13)

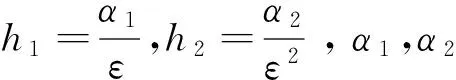
由式(12)得：

(14)

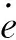
(15)

估计跟踪误差为：

(16)

设计估计滑模为：

(17)

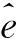
(18)

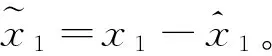
设计控制律τ为：

τt=τ1+τ2，

(19)

(20)

，

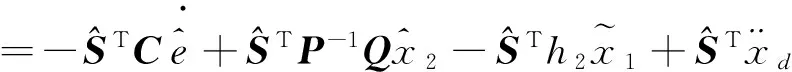
(21)

(22)

其中：λ>0，ξ>0。

李雅普诺夫稳定性证明：

(23)

(24)

将τ1代入式(24)，可得：

(25)

将τ2代入式(25)，得到：

(26)

根据式(12)和(15)可得跟踪误差动态模型：

(27)

实际滑模及其导数为：

(28)

(29)

将控制律(19)代入到(29)可得：

(30)

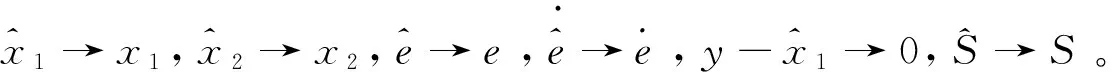
(31)

选取李雅普诺夫函数为：

(32)

(33)

其中，d(t) 0代表干扰和不确定性的上界，显然，只要λ-d0P-1>0，式(33)即可满足滑模条件，跟踪误差渐进稳定。

3 仿真研究

3.1 定位控制

为验证所设计观测器和控制器的有效性，对半潜式海洋平台动力定位过程进行仿真研究。动力学参数矩阵分别为：

(34)

(35)

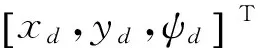
仿真时间T=12s，其他参数分别设置为：

α1=α2=100，ε=0.01，ξ=1，

(36)

(37)

当时间7 s≤t<7.1 s，对系统施加一个额外脉冲干扰f1：

(38)

仿真结果如图3～6所示。

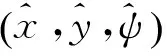
图3 高增益观测器位置信号估计值追踪曲线Fig.3 The estimation tracking curve of position signalfrom high gain observer

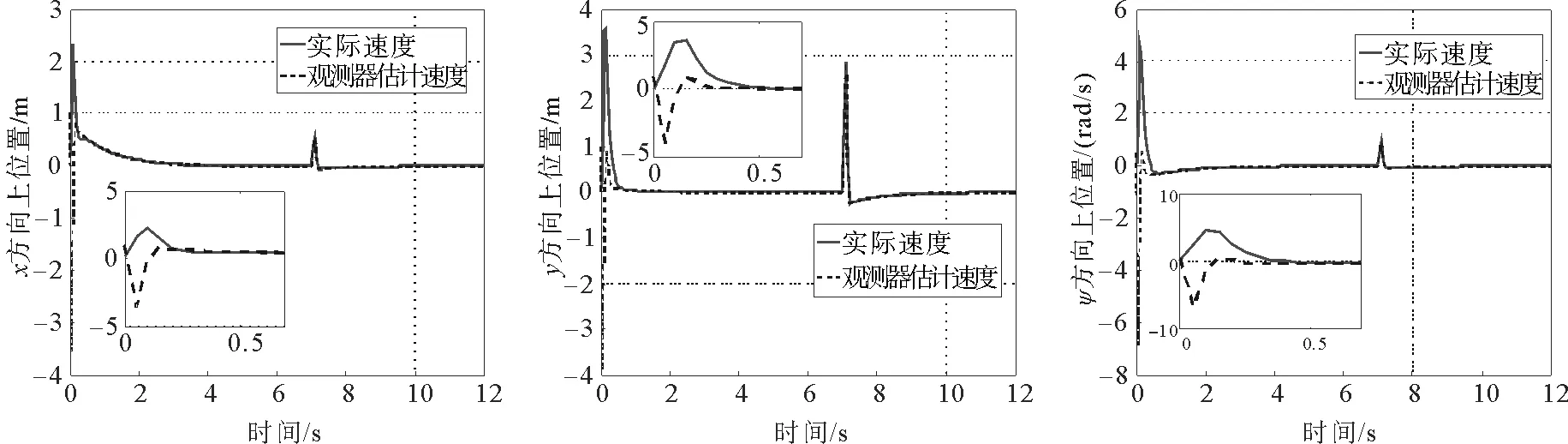
图4 高增益观观测器速度信号估计值追踪曲线Fig.4 The estimation tracking curve of velocity signalfrom high gain observer

图5 实际位置信号x,y,ψ追踪曲线Fig.5 The tracking curve of practical position signalx,y,ψ

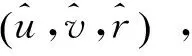
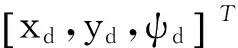
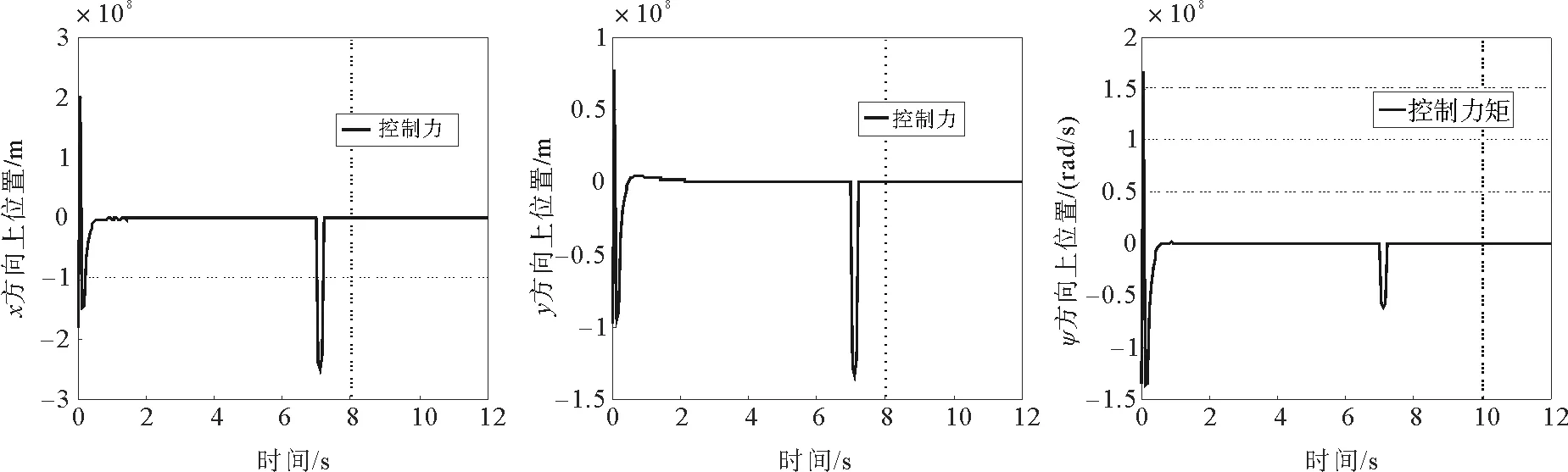
图6 纵荡、横荡方向的控制力和艏摇方向的控制力矩曲线Fig.6 The force & torque curve in surge sway & yaw

2 3.2 轨迹追踪

为进一步验证所设计观测器和控制器的效果，对海洋平台轨迹跟踪过程进行仿真研究。改变期望轨迹及参数λ和ξ，其余各参数设置均与定点控制相同。

当时间5 s≤t<5.1 s，对系统施加一个额外脉冲干扰f2：

(39)

仿真结果如图7～11所示。

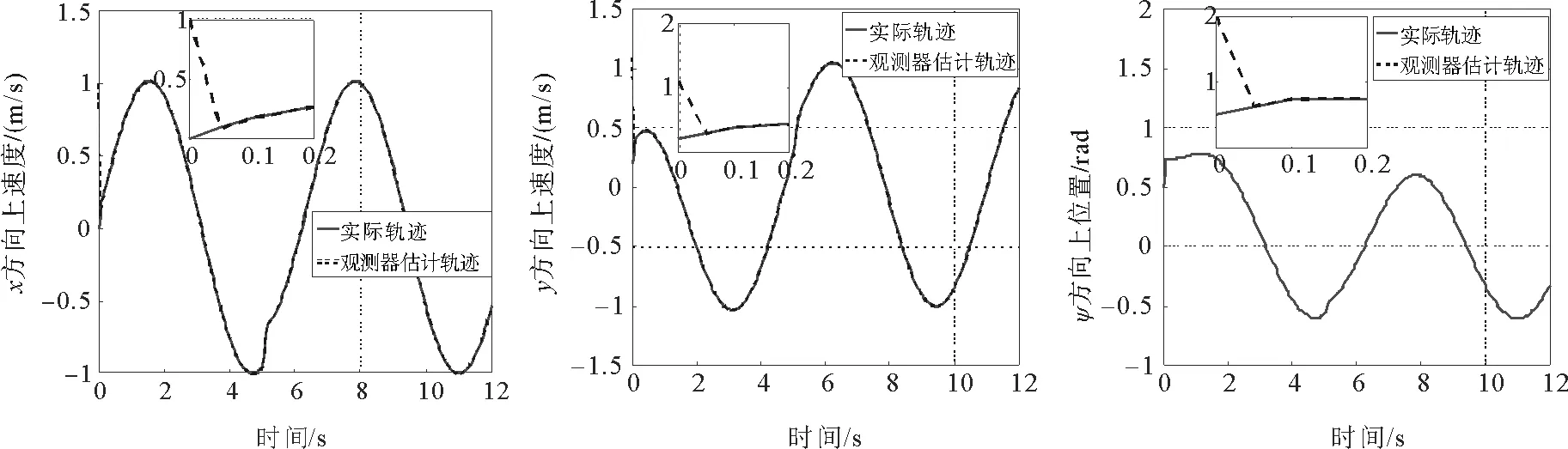
图7 高增益观测器位置信号估计值追踪曲线Fig.7 The estimation tracking curve of position signalfrom high gain observer

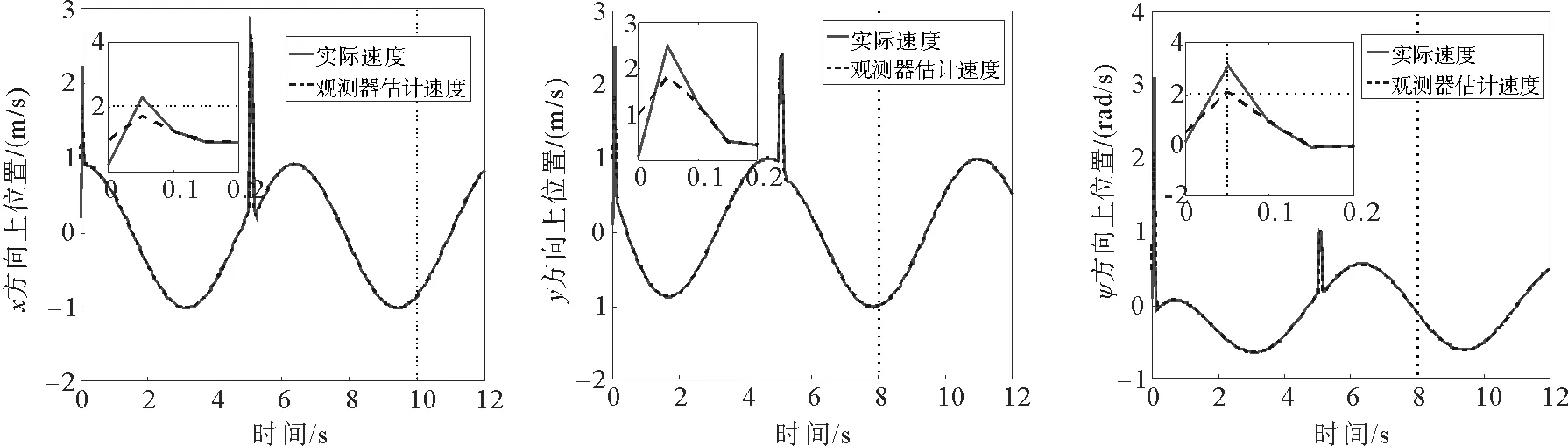
图8 高增益观测器速度信号估计值追踪曲线Fig.8 The estimation tracking curve of velocity signalfrom high gain observer

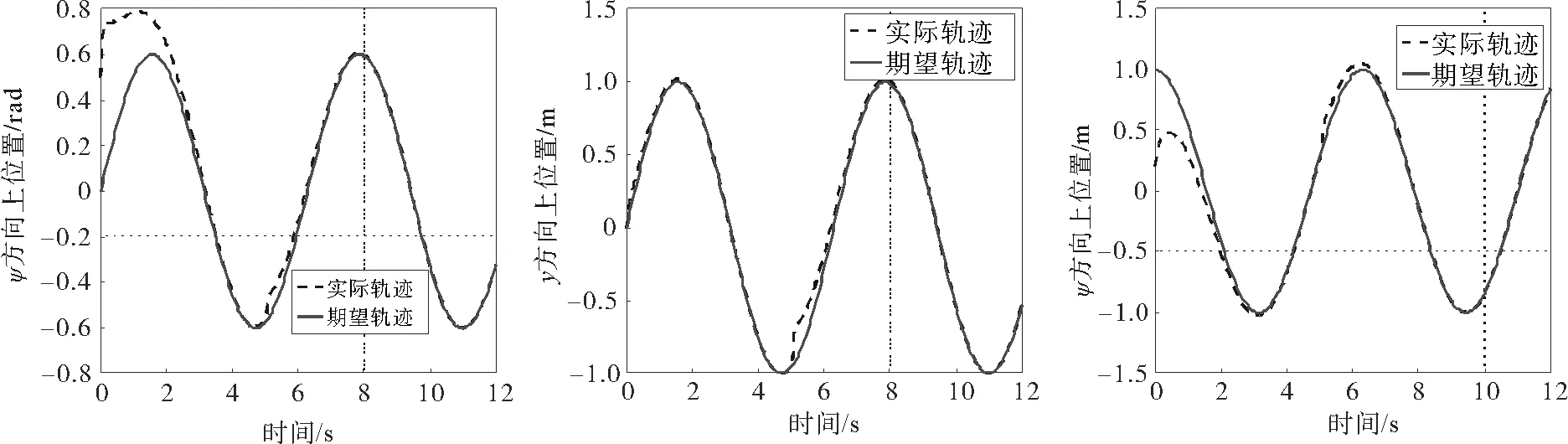
图9 实际位置信号(x,y,ψ)追踪曲线Fig.9 The tracking curve of practical position signalx,y,ψ

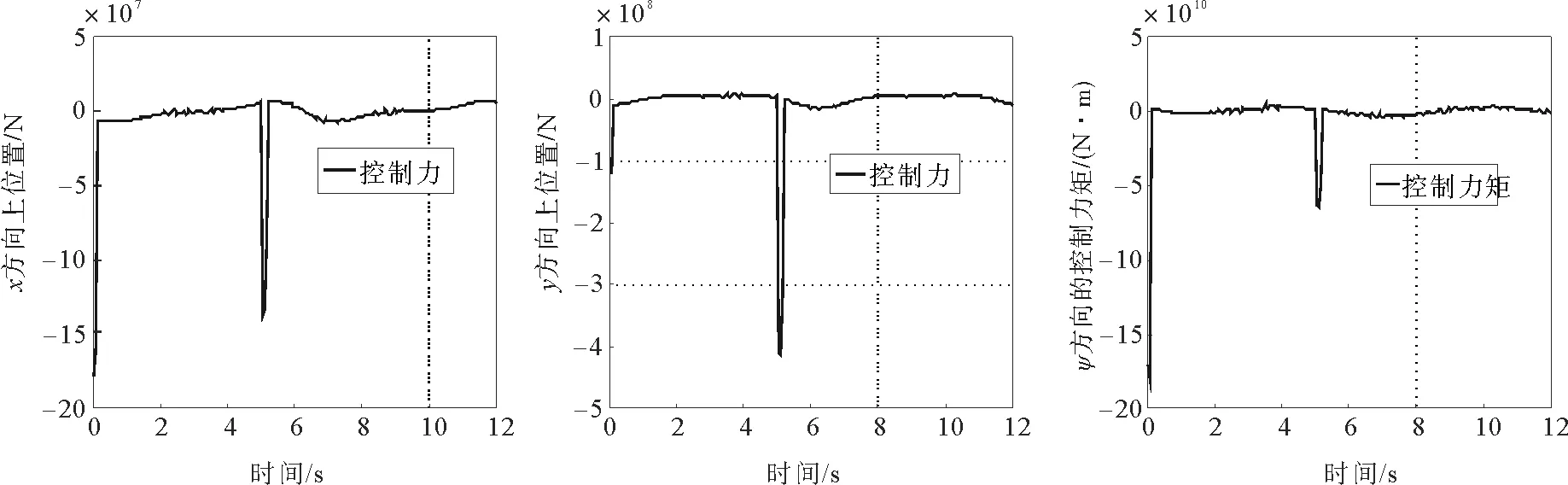
图10 纵荡、横荡方向的控制力和艏摇方向的控制力矩曲线Fig.10 The force & torque curve in surge sway & yaw

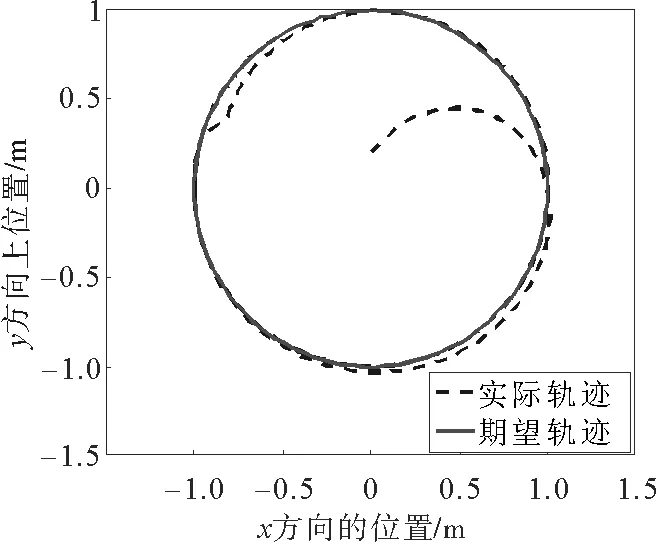
图11 实际海面位置信号(x,y)追踪曲线Fig.11 The tracking curve of practical position signal in x & y plane

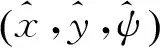
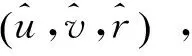
图9为实际位置信号x,y,ψ追踪曲线，由图可知，在t≈3～4 s时，平台的实际位置x,y和艏摇角ψ能够到达期望目标位置，系统达到稳态，当t=5 s时，系统受到脉冲干扰f2，系统稳态被破坏，控制器迅速发生作用，经过3～4 s的短暂过渡过程后，系统重新达到稳态。

图10分别表示纵荡、横荡方向的控制力和艏摇方向的控制力矩曲线。图11为平台在海平面的位置变化曲线，双划线为实际轨迹，实线为期望轨迹，由图可得，所设计控制律能够使平台克服环境因素的干扰，使平台趋向并保持在期望轨迹上，完成整个动力定位过程。当系统受到外界的干扰作用时，控制器能迅速反应，使系统恢复稳态。

4 结论

针对半潜式海洋钻井平台动力定位系统，提出一种基于高增益观测器的鲁棒滑模控制器设计方法。在充分考虑外部环境因素如风、浪、流等干扰及为建模特性影响的基础上，首先通过设计高增益观测器重构出系统的所有状态，得到速度信号，解决了平台速度的不易测量的问题。然后设计鲁棒滑模控制器，用以实现闭环系统的稳定。仿真结果验证了所设计高增益观测器和鲁棒滑模控制器的有效性，能够克服复杂干扰的影响，实现半潜式海洋钻井平台精准的动力定位和轨迹追踪控制，具备较强地抵抗外界干扰的能力，对指导工程实践具有重要意义。

参考文献：

[1]SØRENSEN A J.A survey of dynamic positioning control systems[J].Annual Reviews in Control,2011,35(1):123-126.

[2]SØRENSEN A J.Marine control systems propulsion and motion control of ships and ocean structures[R].Trondheim:Department of Marine Technology,NTNU.2013:1-38.

[3]FOSSEN T I.Handbook of marine craft hydrodynamics and motion control[M].Chichester:John Wiley &,Sons,2011:15-41.

[4]缪燕华,吴斐文.动力定位工程船设计技术研究 [J].上海造船，2010(1):46-50.

[5]FUNG P,GRIMBLE M J.Dynamic ship positioning using a self-tuning Kalman filter[J].IEEE Transactions on Automatic Control,1983,28(3):339-350.

[6]SØRENSEN A J,SAGATUN S I,FOSSEN T I.Design of a dynamic positioning system using model-based control[J].Modeling Identification & Control,1996,17(2):359-368.

[7]TANNURI E A,DONHA D C,PESCE C P.Dynamic positioning of a turret moored FPSO using sliding mode control[J].International Journal of Robust & Nonlinear Control,2001,11(13):1239-1256.

[8]LEIRA B J,SØRENSEN A J,LARSEN C M.A reliability-based control algorithm for dynamic positioning of floating vessels[J].Structural Safety,2004,26(1):1-28.

[9]TANNURI E A,KUBOTA L K,PESCE C P.Adaptive Control strategy for the dynamic positioning of a shuttle tanker during offloading operations[J].Journal of Offshore Mechanics and Arctic Engineering,2006,128(3):203-210.

[10]TANNURI E A,AGOSTINHO A C,MORISHITA H M,et al.Dynamic positioning systems:An experimental analysis of sliding mode control[J].Control Engineering Practice,2010,18(10):1121-1132.

[11]DORLING C M,ZINOBER A S I.Two approaches to hyperplane design in multivariable variable structure control systems[J].International Journal of Control,2012,44(1):65-82.

[12]何黎明,田作华,施颂椒.动力定位船舶的非线性观测器设计[J].上海交通大学学报,2003,37(6):964-968.

HE Liming,TIAN Zuohua,SHI Songjiao.The nonlinear observer design of dynamic positioning offshore ship[J].Journal of Shanghai Jiaotong University,2003,37(6):964-968.

[13]SØRENSEN A J.Structural issues in the design and operation of marine control systems[J].Annual Reviews in Control,2005,29(1):125-149.

[14]CUNHA J P V S,COSTA R R,LIZARRALDE F,et al.Peaking free variable structure control of uncertain linear systems based on a high-gain observer[J].Automatica,2009,45(5):1156-1164.