海上浮式风机平台的水动力分析
徐思远,张淑华
(河海大学 港口海岸与近海工程学院,南京 210098)
风能作为一种可再生能源,具有广阔的应用潜能[1],因此得到广泛的重视,风电的开发和利用发展迅速[2]。目前海上风机平台以近海海域的固定式平台为主,但是近海海域的资源有限,而深海海域空间广阔并且有丰富的风能资源,从而吸引了更多专家学者致力于海上浮式风机的研究[3]。与近海固定式平台相比,深海浮式平台所遭受的海洋环境更恶劣,运动响应也更加剧烈,这对风机的平稳运行是一个巨大的考验[4]。目前,研究较多的海上浮式风机基础主要有SPAR型基础[5]、TLP型基础[6]、半潜式基础和浮筒基础等。本文针对200 m水深海域,设计了支撑5MW风机的SPAR型基础,分别在频域和时域内对平台进行了分析,计算得到了平台的幅值响应算子,附加质量等水动力系数,以及在不同风况下风机平台运动的时历曲线。最后,计算了风机在百年一遇海况条件下的运动响应,证明了其能够在深海海域安全运行。

1-a SPAR平台结构模型图 1-b 系泊系统布置示意图图1 SPAR平台结构模型Fig.1 Structure model of SPAR
1 平台结构参数
SPAR浮式平台由浮箱、垂荡板、立柱和压载舱4个部分组成,如图1所示,平台总体高度为66 m。浮箱为圆柱式,垂荡板为三层,最底部为混凝土压载舱,各部分由立柱连接。浮箱提供浮力和回复力,垂荡板增加平台阻尼[7],抑制垂荡运动,压载舱中填充混凝土,降低系统重心,平台结构的参数如表1所示。由于水面线处的大尺度结构会使平台垂荡固有周期接近波浪谱的高能量区域[8],从而造成较大的垂荡响应,因此在设计的过程中将浮箱分为两个部分,上部分的小尺度结构(浮箱1)可以减少平台的垂荡响应和所受的波浪力,下部分的大尺度结构(浮箱2)为浮式基础提供足够的浮力。平台重心和浮心的高度差为17.2 m,说明该平台可以在水中保持足够的稳定性。

表1 平台结构参数Tab.1 Structure parameters of the platform
风机采用美国可再生能源研究所(NREL)公布的5MW风机进行建模和计算[9]。风机的主要参数如表2所示。系泊系统采用8根系泊缆均匀对称布置的形式,锚链参数如表3所示[10],系泊系统的布置如图1所示。

表2 风机发电参数Tab.2 Parameters of wind turbine

表3 锚链参数Tab.3 Parameters of mooring system
2 环境条件
不规则波浪使用Pierson-Moscowitz谱生成。假设不规则波是由风引起的,在无风区尺度限制的深海条件下,根据经验公式可以计算在某个风速下的有义波高H1/3。有义波高H1/3和U的关系由以下经验公式表达
(1)
不规则波和均匀定常风计算工况如表4所示。

表4 不规则波工况Tab.4 Loading conditions of irregular waves
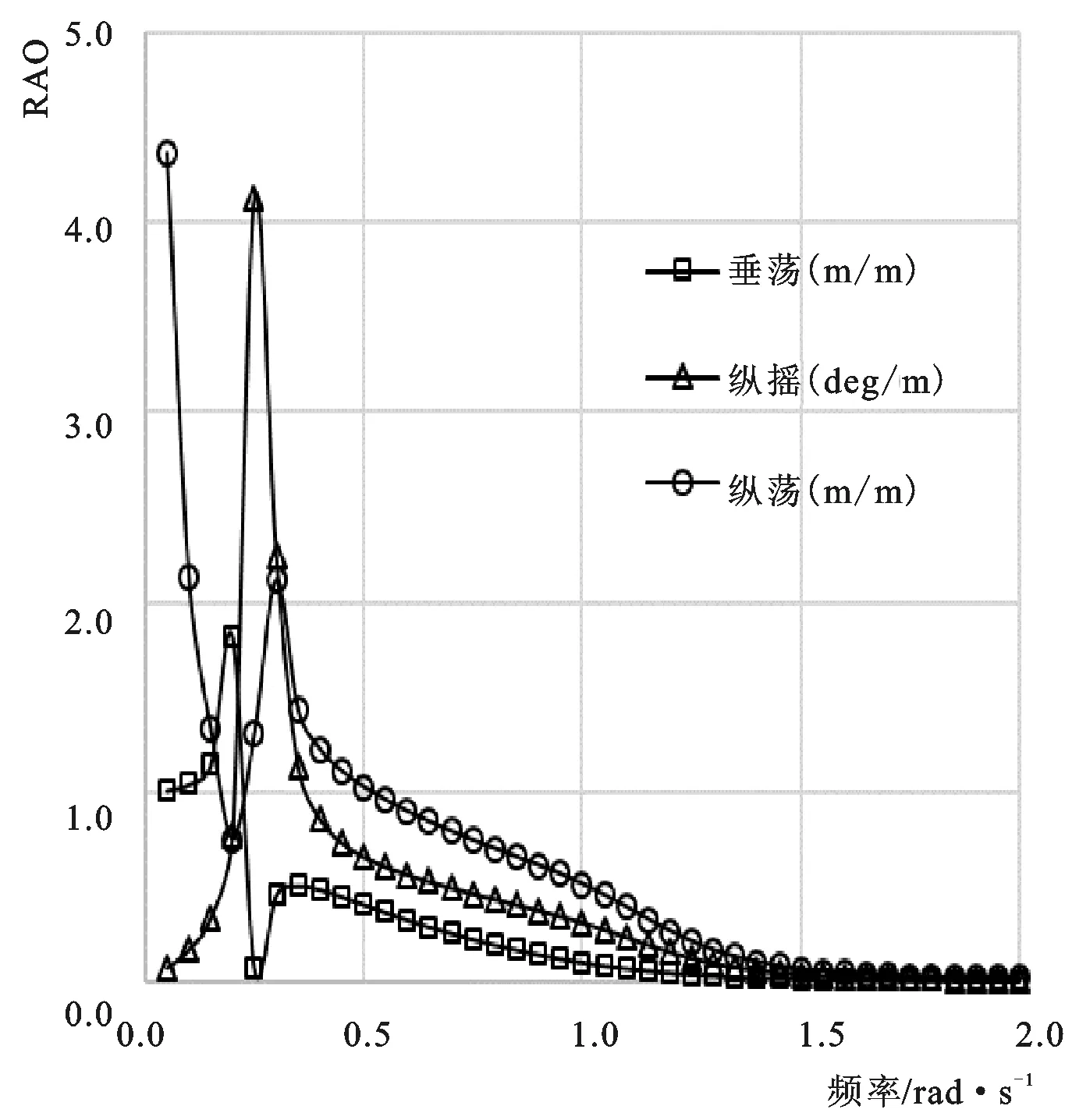
图2 SPAR风机平台的幅值响应算子Fig.2 RAO of the wind turbine
3 风机平台频域响应分析
平台的频域分析使用SESAM的势流模块HydroD。频率范围取0~2 rad/s,来波方向0°,工作水深200 m。计算得到风机平台运动的幅值响应算子。由于平台的对称性,横荡、横摇和艏摇均为0。平台的纵摇、纵荡和垂荡如图2所示。从图中可以看出,当波浪频率接近平台的固有频率时,平台的各个自由度的运动剧烈,而波浪频率远离固有频率时,平台的运动趋于缓和。平台纵摇和纵荡的固有频率在0.3 rad/s左右,垂荡的固有频率在0.2 rad/s左右。因此,平台的固有频率在0.2~0.3 rad/s左右,该频率远离常见的波浪频率。这说明设计出来的平台具有良好的耐波性。计算得到的幅值响应算子,附加质量系数,势流阻尼系数等水动力参数将会用于时域分析中。
4 风机平台时域响应分析
NREL 5MW风机为可控叶片螺距型,即在不同的风速下可以通过改变风机叶片的螺距来使发电机的功率保持稳定。均匀定常风作用于该叶片上的推力,可以用基于Knauer等提出的经验公式计算[11]
(2)
式中:ρa为空气密度;A为叶片扫过的面积;Ur为来风与风机的相对速度;CT为风机叶片的推力系数,是与风速相关的函数。
计算得到的不同风速下作用于叶片上的推力见表5。当风速达到11.4 m/s时,风机所受的风力最大。

表5 作用于风机叶片的推力Tab.5 Wind force on turbine blades
4.1 不规则波和定常风作用下的平台运动响应
使用SESAM[12]软件中的DeepC模块计算风机系统的运动响应和锚链张力。由于风速和风向随时间的变化较为缓慢,因此在一定的时间段内可以认为风速和风向是不变的,并且在风速较大时不考虑涡激振动的影响,只考虑均匀定常风及其引起的不规则波一起作用于浮式平台上,定常风和不规则波来向均为0°。计算得到风机平台运动响应和锚链张力(Line1)的时历曲线,并对时历曲线进行频谱分析,结果见图3。

3-a 纵荡频谱 3-b 纵摇频谱
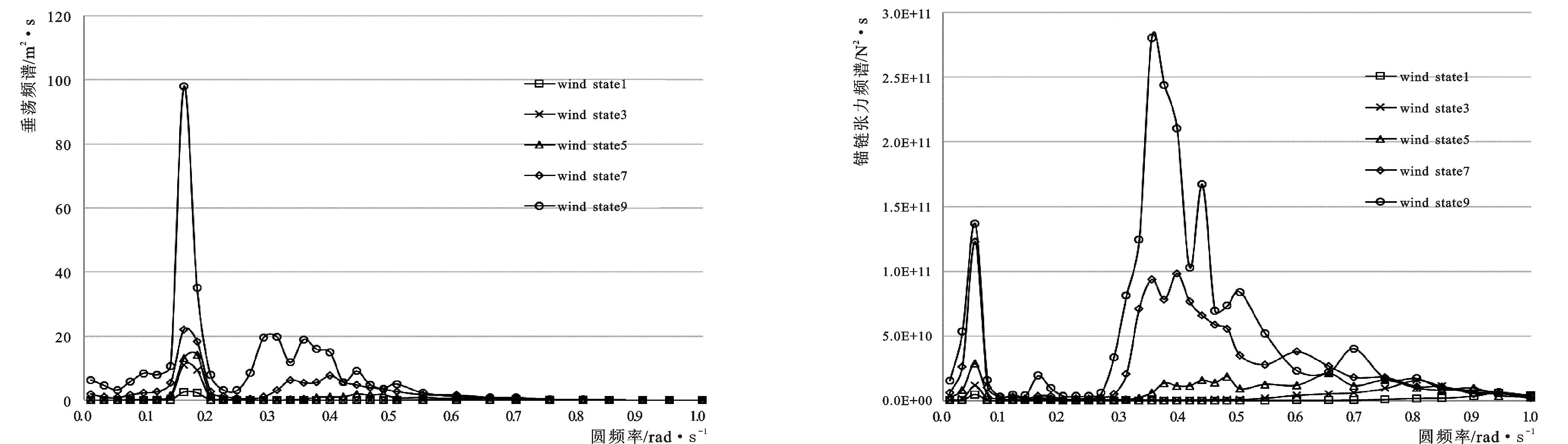
3-c 垂荡频谱 3-d 锚链张力频谱图3 SPAR风机平台运动和锚链张力的频谱分析Fig.3 Spectrum analysis of platform motions and line′s tension
从图3中可以看出,平台的运动可分为频率为波频的高频运动以及频率约为0.05 rad/s或0.2 rad/s的低频运动,并且低频运动的频率不随风速和波浪大小的变化而变化。平台运动和锚链张力频谱波频部分的谱峰,随着不规则波有义波高的增大以及谱峰频率的减小,也相应的增大并往低频处偏移。
提取不同风况下对平台运动和锚链张力的时历曲线的最大值,得到不同风速下平台运动和锚链张力最大值的曲线图,见图4。从图4中可以看出,纵摇、纵荡和锚链张力的最大值在总体上随风速增大而增大,而在风速达到11.4 m/s后由于风对风机叶片的推力减小,最大值的变化趋于平缓,随后由于波浪的增大而继续增大。平台垂荡的最大值随风速的增大一直在增大,平台风机叶片的推力对其几乎没有影响。平台的纵摇和垂荡在风速25 m/s的时候达到最大值,而纵荡和锚链张力在风速23 m/s的时候达到最大值。平台的运动在20 m/s后达到一个较大值,因此建议在风速达到20 m/s后,风机暂时停止运转,即处于自存状态。
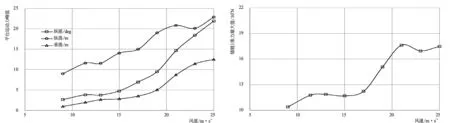
4-a 不同风速下平台运动最大值 4-b 不同风速下锚链1张力最大值图4 不同工况下SPAR风机运动和锚链张力的最大值Fig.4 The maximum values of platform motion and line′s tension under different conditions
4.2 不规则波作用下的平台运动响应
风机的切出风速为25 m/s,因此风速大于25 m/s以后风机停止转动,处于自存状态。选取百年一遇台风极限海况[13],海浪谱选择Bretschneider谱,Hs=13.3 m,Ts=15.5 s,波浪入射角为0°。计算得到风机平台运动和锚链张力的时历曲线。根据锚链张力的时历曲线提取出锚链张力的最大值,见表6。根据平台运动的时历曲线提取出各自由度的最大值,其中纵摇运动的最大值为15°,纵荡运动的最大值为19.3m,垂荡运动的最大值为9.9m。依据API规范要求,对于百年一遇海洋条件下自存工况的海洋平台,完好的系泊系统进行动力分析时,钢链和钢缆的最大张力安全因子取1.67。平台的最大水平位移应控制在水深10%的范围以内。安全因子是锚链最大张力与锚链破断强度的比值。从表6中可以看出,平台最大锚链张力出现在5号锚链,安全因子为4.48,满足API规范的要求。从表7中得知,平台纵荡最大值为19.3 m,没有超过水深的10%。因此平台在台风极限海况下运动响应良好,能够适应深海恶劣的海洋环境。
5 结论
(1)SPAR风机平台纵摇和纵荡的固有频率在0.3 rad/s左右,垂荡的固有频率在0.2 rad/s左右,该频率远离常见的波浪频率,平台具有良好的耐波性。
(2)分析SPAR平台运动时历曲线的频谱得知,风机系统的运动可分为两个部分:一个是与平台固有频率和系泊系统有关的低频运动,另一个是与波浪频率有关的高频运动。
(3)对不同风速下平台运动和锚链张力最大值分析,在风速达到20m/s后,平台运动的最大值达到了较高的水平。建议在风速到达20 m/s时,风机叶片停止运转进入自存状态。
(4)平台在百年一遇的台风极限海况下运动响应良好,能够适应深海恶劣的环境。说明该SPAR风机平台设计合理。
参考文献:
[1]黄维平, 刘建军, 赵战华. 海上风电基础结构研究现状及发展趋势[J]. 海洋工程, 2009,27(2): 130-134.
HUANG W P, LIU J J, ZHAO Z H. The state of the art of study on offshore wind turbine structures and its development[J]. The Ocean Engineering, 2009, 27(2):130-134.
[2]张蓓文, 陆斌. 欧洲海上风电场建设[J]. 上海电力,2007(2):129-135.
ZHANG B W, LU B. Construction of Offshore Wind Turbine in Europe[J]. Shanghai Electric Power,2007(2):129-135.
[3]阮胜福. 海上风电浮式基础设计与运动响应研究[D].天津:天津大学,2010.
[4]Wang C M, Utsunomiya T, Wee S C, et al. REVIEW PAPER: Research on Floating Wind Turbines: A Literature Survey[J]. The IES Journal Part A: Civil & Structural Engineering, 2010, 3(4):267-277.
[5]张大朋, 朱克强. Spar型海上浮式风机系泊系统的动力分析[J].水道港口,2017,38(4):398-404.
ZHANG D P, ZHU K Q. Dynamic analysis of the mooring system for a floating offshore wind turbine Spar platform[J]. Journal of Waterway and Harbor, 2017,38(4):398-404.
[6] 严心宽, 朱克强, 张大朋,等. 海上浮式风机张力腿平台的水动力响应[J].水道港口,2016,37(1):46-54.
YAN X K, ZHU K Q, ZHANG D P, et al. Hydrodynamic response of a floating offshore wind turbine tension leg platform[J]. Journal of Waterway and Harbor, 2016,37(1):46-54.
[7] 刘中柏. 海上风电浮式基础运动特性试验研究[D].天津:天津大学,2014.
[8] 曹菡. 海上风机半潜型浮式基础水动力性能研究[D].天津:天津大学,2012.
[9] Jonkman J, Butterfield S. Definition of a 5-MW Reference Wind Turbine for Offshore System Development[R]. Golden, CO (United States): NREL, 2009.
[10] Jonkman J. Definition of the Floating System for Phase IV of OC3[R]. Golden, CO (United States): NREL, 2010.
[11] Knauer A, Hanson T D, Skaare B.Offshore Wind Turbine Loads in Deep-water Environment[C]//Proceedings of the European Wind Energy Conference & Exhibition. Athens, Greece: EWEC, 2006.
[12] DNV-OS-J101, Design of Offshore Wind Turbine Structures[S].
[13] 李牧, 田冠楠, 杨凯东. 南海FPSO超极限海况下抗风能力分析[J].船海工程, 2016, 45(5): 1-5.
LI M, TIAN G N, YANG K D. On the Ultimate Wind Resistant Ability of the FPSO in South China Sea[J]. Ship & Ocean Engineering, 2016, 45(5):1-5.

