基于某卫星通信系统的信号捕获研究

刘文华

（北京空间信息中继传输技术研究中心，北京 100094）

1 引言

当前，战争形态正加速向信息化战争演进，装备的发展进入一个适度创新、催生新质能量的崭新阶段。卫星通信在现代军事行动中之所以作用越来越大，地位越来越重要，关键原因在于卫星通信可完成众多的军事任务，诸如转发语音和数据、搜集图片和信号情报等，特别是在远程军事通信中更见其独特威力，它为军事指挥官提供的灵活性、实时性以及战术机动性均是其他通信方式难以实现的[1]。

由于通信卫星和用户接收机之间的相对运动引起的多普勒效应、接收机晶体振荡频率漂移和卫星时钟频漂等因素，接收机实际接收到的卫星信号频率不再等于信号发射时的标称频率，同时，卫星与接收机的距离时刻在发生变化，因而接收信号的码相位也在时刻变化[2]。

接收机跟踪环路精密而脆弱。为了让接收机在启动后成功地跟踪、锁定卫星信号，接收机必须事先能估算出卫星信号的载波频率和码相位，并且载波频率和码相位的误差必须分别小于载波环和码环的迁入范围，然后接收机根据事先估算出的载波频率和码相位初始化载波跟踪环路和码跟踪环路，这样跟踪环路才能对卫星信号进行迁入与镇定，直至最后成功地进入正常的跟踪状态[3]。而信号捕获的目的正是为了获取卫星信号的载波频率和码相位的粗略估计值。

2 传统的信号捕获算法

当接收机与卫星之间发生相对运动时，会产生多普勒效应[4]，即接收机接收到的信号频率不再是卫星发射的频率，接收机接收到的信号频率与卫星发射频率之间存在如下关系：

式中，fr是接收机接收到的卫星信号频率；f是卫星发射的信号频率；fd为多普勒频移。从电磁波传播理论出发，可以推导出fd的计算公式：

式中，c为光速；v是卫星与接收机之间的相对运动速度的径向分量。当武器平台与卫星之间的相对运动速度较大时的径向分量，相应的多普勒偏移也会很大，同时武器平台与卫星之间的距离时刻在变化，导致接收信号的码相位也在时刻变化，这就需要接收机在载波频率和码相位二维内对卫星信号进行捕获。

卫星信号的捕获是一个二维搜索过程[5]，如图1 所示。图中，fbin为载波频率的搜索步长，tbin为码相位的搜索步长，通常码相位的搜索步长为半个码片。

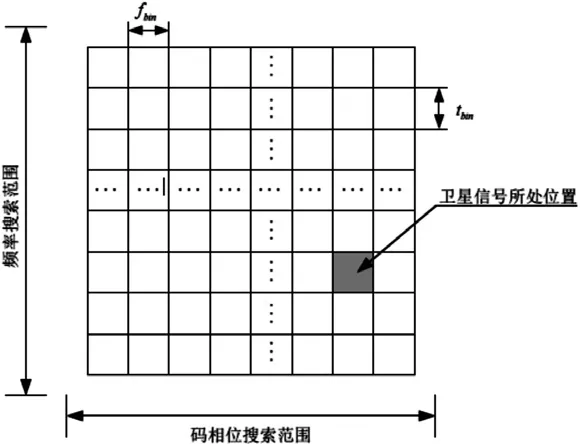
图1 卫星信号捕获的二维搜索

根据伪码的自相关特性和频偏对伪码相关峰值的影响可知，只有当本地载波频率与接收到的卫星信号频率接近，且接收机本地伪码与接收到的卫星信号伪码相位对齐时，本地伪码与经过下变频后的卫星信号进行相关运算才会产生最大的相关峰[6]。因此可以通过判断每个搜索单元的相关峰值是否超过设定的门限值，来判断信号捕获是否成功，若在搜索过程中，某个搜索单元的相关峰值超过门限，则相应单元的载波频率和码相位值即为卫星信号的载波频率和码相位。

传统的卫星信号捕获原理如图2所示[7][8]，首先对接收到的卫星信号进行混频处理，并将混频结果与接收机的本地伪码进行相关运算得到i和q，随后将相关后的结果进行时间为Tcoh的相干积分后得到相干积分结果I和Q，最后对Nnc个相干积分结果进行非相干积分，得到非相干积分幅值V。对非相干积分幅值V进行判断，若V小于门限Vt，则认为还没有捕获到卫星信号，捕获控制器按照预先设计的频率搜索步长和码搜索步长调节载波NCO和C/A码发生器，继续在下一个搜索单元搜索。若非相干积分结果V大于门限Vt，则判定已捕获到卫星信号，随后将该搜索单元对应的载波频率和码相位置给后面的环路滤波器进行环路跟踪。

图2 传统卫星信号捕获原理框图

若多普勒频移的搜索范围为fdHz，则信号捕获频率搜索范围为-fdHz～fdHz，那么频率糟个数为

对应每个频率槽的频率为0Hz，fbinHz，-fbinHz，fdHz，-fdHz，当伪码长度为tunc，伪码搜索步长为半个码片时，传统卫星捕获搜索的单元数为

从而可以计算出，传统卫星信号捕获算法最长捕获时间为

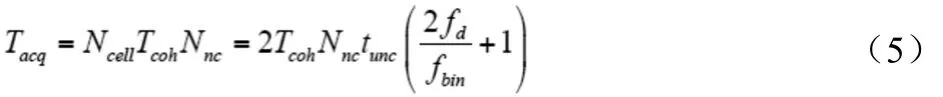
3 改进的信号捕获算法

传统的信号捕获方法每次只搜索一个单元，所以它的捕获速度很慢。本文提出一种并行捕获算法，通过傅里叶变换实现对频率的并行搜索，同时配备多个相关器，对多个码相位同时进行搜索，从而加快了信号捕获速度。

并行搜索算法原理框图如图3所示，输入信号与接收机内部载波相乘进行混频，将混频后的信号与多路接收机本地伪码进行相关运算，以实现并行码相位搜索。每路码相位下捕获流程为：对相关运算后的结果进行相干积分得到I和Q，对N个（一般为2的幂次）I+jQ数据进行傅里叶变换，最后对傅里叶变换后的数据进行分析，若最大值超过门限，则认为已捕获到卫星信号，且该路接收机本地伪码与接收信号中的伪码对齐，最大值对应的频率为多普勒频移。

根据FFT理论，若并行捕获算法相干积分后的频率为fs，N点FFT变换后的前一半结果对应频率为0～fs/2，后一半结果对应的频率为-fs/2～0，其中并行捕获算法的频率分辨率为fs/N。根据前面分析可知，高动态环境下，接收机的最大多普勒频移为35kHz，所以并行捕获算法的相关积分时间不能超过1/70ms，否则并行捕获算法不能对卫星信号进行捕获。

图3 并行捕获算法原理框图

4 结束语

卫星通信在通信中的地位越来越重要，在高动态环境下，由于接收机多普勒频移和码相位不确定性，需要进行信号捕获才能正常通信。传统的信号捕获方法捕获时间长，无法满足需求。本文对并行捕获算法进行了研究，通过傅里叶变换实现对频率的并行捕获，同时配备多个相关器，在码相位上进行并行捕获，理论分析和仿真结果表明，该并行捕获算法在高动态环境下能有效地捕获到卫星信号，并提高了捕获时间。

[1] 易克初，李怡，孙晨华，南国春.卫星通信的近期发展与前景展望[J].通信学报，2015（6）.

[2] 胡娟.一种基于并行FFT的pn码快速捕获算法实现[J].电子科技，2011，24（7）：109-111.

[3] 刘佳欣，崔国强，陆乐乐.扩频信号基于FFT 码捕获的计算量分析[J].现代电子技术，2012，35（19）：29-31.

[4] 郭兴阳.基于FPGA的匹配滤波器的优化设计与实现[D].西安电子科技大学，2011：25-29.

[5] 陈希，张锐，帅涛.基于FFT的GPS快速并行捕获算法[J].宇航学报，2011，32（1）：162-166.

[6] Spangenberg S M，Scott I，McLaughlin S，et al.An FFT-based approach for fast acquisition in spread spectrum communication systems[J].Wireless Personal Communications，2000，13（1-2）：27-55.

[7] Yong C，Hang-Sheng Z.Design and Realization of Fast Code Acquisition for Long PN Code Spread Spectrum Communication in LEO Satellite[C]//Communications，Circuits and Systems Proceedings，2006 International Conference on.IEEE，2006，2：1161-1164.

[8] Dovis F，Ta T H.High Sensitivity Techniques for GNSS Signal Acquisition[J].2012，3-23.