高性能氮化铝差分谐振式加速度计的结构设计
高 杨,韩 超,雷 强
(1. 中国工程物理研究院 电子工程研究所,四川 绵阳 621999;2. 中国科学院高能物理研究所 核探测与核电子学国家重点实验室,北京 100049;3. 西南科技大学 信息工程学院,四川 绵阳 621010)
微加速度计广泛应用于先进的军事设备和常见的消费电子产品,可测量运载体的加速度,用于惯性导航或全球定位等[1]。微机械谐振式加速度计(MMRA)具有成本低、体积小、量程大、灵敏度高和稳定性好等优点。这类传感器直接把所测的加速度转化为频率输出,避免了幅度测量的误差,不易受到环境噪声的干扰,而且准数字输出可简化接口电路,在传输和处理过程中也不易出现误差[2]。MMRA有多种工作原理,从传感器原理上可以分为两大类:位移敏感和力敏感。位移敏感测量可动质量块的位移,位移检测方式包括电容[3-4]、电磁[5]、光学等。力敏感是通过测量质量块的惯性力来测量加速度的,惯性力检测方式包括压阻[6]、压电[7-8]等。谐振式加速度计可归为力敏感这一类。
根据谐振器材料的压电特性,MMRA又可分为压电MMRA(石英和AlN)和非压电MMRA(硅)。硅MMRA通常受下拉效应的限制,并且制造工艺复杂,品质因数(Q)相对较低[9]。石英和氮化铝(AlN)固有的压电特性使得它们广泛用作MEMS谐振器材料,因为其具有高Q值,良好的化学稳定性等[10-11]。但石英很难与CMOS工艺兼容,在组装过程中需要很高的精度,以防残余应力修改石英谐振器的频率[12]。AlN与CMOS工艺兼容,因此在CMOS电路上集成AlN谐振式加速度计,可进一步减小尺寸和降低成本,提高读出电路的稳定性。Roy H. Olsson等首次提出了基于AlN双端固支音叉(DETF)谐振器的MMRA,并且在基频为890 kHz情况下的灵敏度为3.4 Hz/g[13]。Vigevani G等通过引入单级微杠杆,采用―U‖形结构的支撑梁,增加质量块的面积来优化AlN谐振式加速度计的结构[14]。灵敏度从3.4 Hz/g增加到18.1 Hz/g,横向灵敏度为0.1 Hz/g。与静电激励的硅MMRA相比,灵敏度和横向灵敏度的性能仍然较差。MMRA的性能通常受温度的影响,但上述AlN谐振式加速度计都未对温度灵敏度进行分析测试。
本文提出了一种高性能的AlN谐振式加速度计结构,通过引入两级微杠杆来放大质量块的惯性力,提高灵敏度。采用一种―I‖形支撑梁来降低横向灵敏度,并利用差频检测方案降低温度共模误差的影响。与之前报道的 AlN谐振式加速度计[13-14]相比,所提出的加速度计具有更高的灵敏度,更低的横向干扰。热应力仿真结果验证了差频检测方案可有效降低温度共模误差的影响。
1 结构和原理
1.1 表 头
本文设计的AlN差分谐振式加速度计表头由质量块、支撑梁、谐振器(DETF)和双级微杠杆构成,如图 1(a)所示。当在加速度计的敏感方向施加一个加速度时,质量块的等效惯性力作用于两个AlN DETF谐振器(一个被压缩,另一个被拉伸),谐振器的刚度发生变化,导致谐振器的谐振频率偏移,频率偏移量与加速度大小成正比。采用推挽结构并实现差分检测,不仅可以使灵敏度加倍,还可以减小外部环境共模误差的影响[15-16]。双级微杠杆用于放大质量块的等效惯性力,可将灵敏度提高一个数量级[17-18]。图 1(a)的插图为―I‖形支撑梁,该梁在检测方向具有较低的刚度,在交叉轴方向具有很大的刚度,这样可以降低加速度计的横向灵敏度,增强抗干扰能力[19]。
AlN DETF谐振器的结构如图1(b)所示。在驱动梁上施加驱动电压,产生一个沿z轴方向的电场E3,由于压电应变系数d31的作用,谐振梁内会产生一个面内应变。当驱动电压的频率等于谐振梁的固有频率时,就会产生谐振[11]。通常将DETF谐振器的面内对称模态作为工作模态,这是由于两个音叉臂在它们的合并区域产生的应力和力矩方向相反,互相抵消,整个结构与外界的能量耦合小,具有较高的Q值[2]。为了得到面内对称模态,通过驱动电压激励的面内应变必须与谐振梁横向振动时的应变一致,因此需要对电极的分布进行图形化,如图1(c)所示。电极呈对称分布,材料通常为铂,宽度为谐振梁的 1/2。这种两端口对称电极设计可以减少谐振时的馈通电容,增加相移[20]。
1.2 微杠杆

图1 AlN差分谐振式加速度计:(a) 表头和―I‖形支撑梁的结构;(b) 谐振器的结构;(c) 电极分布;(d) 面内对称模态(仿真)Fig.1 Schematic view of the proposed AlN differential resonant accelerometer: (a) structure of sensor head and I-shape supporting beam ; (b) structure of AlN resonator; (c) electrodepattern; (d) in-plane symmetrical mode(simulation)
为了进一步提高灵敏度,AlN谐振式加速度计引入两级微杠杆系统来放大质量块的惯性力。微杠杆的结构如图2所示,第一级微杠杆与质量块连接,第二级微杠杆与连接块连接,两个微杠杆通过连接梁(第一级的输出梁,第二级的输入梁)耦合,并且都是第二类杠杆(输出梁在中间)[17]。质量块的惯性力作用于第一级微杠杆的输入梁,经双级微杠杆放大后,通过第二级微杠杆的输出梁作用于AlN DETF谐振器。
双级微杠杆的放大系数A可定义为输出力Fout(连接块上的轴向载荷)与输入力Fin(输入梁上的轴向载荷)的比值,即每个微杠杆放大系数的乘积[17]。

图2 双级微杠杆的结构Fig.2 Schematic of two-stage micro-leverage mechanism

其中:A1和A2分别为第一级和第二级微杠杆的放大系数;和分别为第i级微杠杆支点梁的轴向和弯曲刚度;和分别为第i级微杠杆输出梁的轴向和弯曲刚度;li为第i级微杠杆的阻力臂长度;Li为第i级微杠杆的动力臂长度。并且,其中,E为梁的杨氏模量,Ar为梁的横截面面积,I为梁的截面惯性矩。
根据式(1)~(3),提高单级微杠杆放大系数的方法有两种:第一种,减小某些梁(支点梁和输出梁)的宽度,同时增加它们的长度,但是会造成加速度计的结构强度和稳定性恶化;第二种,增大杠杆比(L / l),但是会导致器件的尺寸增大。
多级微杠杆可在有限的空间内进一步提高放大系数,但这并不代表微杠杆的级数越多,灵敏度越高。随着微杠杆的级数增加,整个系统的弹性常数降低,对加速度计的性能有较大的影响[21]。因此,本文采用两级微杠杆来优化放大系数和器件尺寸。
1.3 灵敏度
当在敏感轴(y轴)方向施加一个加速度时,其中一个谐振器被拉伸,频率增大,另一个谐振器被压缩,频率减小。根据经典的 Euler-Bernoull梁理论,DETF谐振器的谐振频率为[18]:
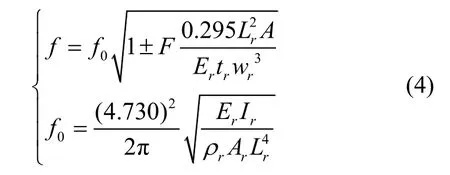
其中,―+‖表示拉伸应力,―-‖表示压缩应力,F为轴向应力的幅值,Lr、wr、tr分别为振梁的长度、宽度、厚度,f0为振梁横向振动的基频,Er为振梁的杨氏模量,Ir为振梁的截面惯性矩,为振梁的密度。
两个谐振器的输出差频为:
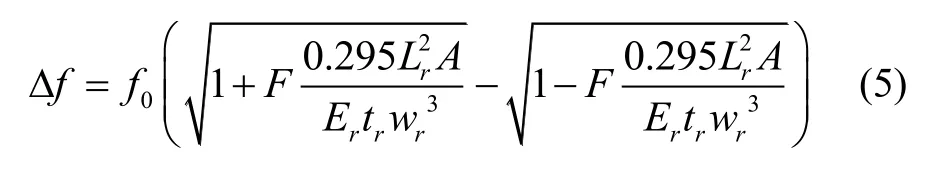
对式(5)进行泰勒展开,并忽略高阶项:
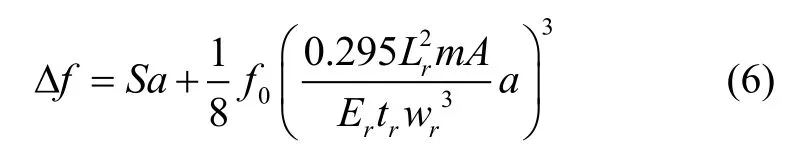
2 方 法
基于Euler-Bernoulli梁理论和Timoshenko梁理论的DETF谐振器被广泛研究。这些理论假设谐振梁的两端固定,两个谐振梁之间不存在机械耦合,因此可以得到谐振梁横向振动的近似解。但是对于 MEMS尺寸的器件,这些理论存在缺陷:两个谐振梁存在机械耦合。这对整个谐振器的动态特性有重要影响[11],所以想要得到 AlN DETF的近似理论解是十分困难的。为了优化振梁的结构参数, 可以在有限元软件中建立其多物理场模型并计算它的特征参数。文献[22]给出了AlN DETF谐振器振梁结构参数的优化设计原则,本文中振梁的结构参数与文献[22]优化后的结果一致,长度Lr=300 µm,宽度wr=4 µm,厚度tr=2 µm。
双级杠杆的放大倍数为两个杠杆放大倍数的乘积,因此可以先仿真优化得到第一级杠杆支点梁的最优位置,并在该基础上联合第二级杠杆,分析第二级杠杆支点梁的位置,使得双级杠杆的放大倍数最大。在仿真优化得到其他梁的长度和宽度后,分析一级杠杆的力放大系数,结果如图 3(a)所示。当阻力臂长度l1=8 μm时(动力臂(总长)L1=430 μm),力放大系数最大(16.2253)。联合第二级杠杆,仿真优化第二级杠杆阻力臂长度l2,得到整个双级杠杆系统的力放大系数(l1=8 μm,L2=460 μm),如图 3(b)所示。

图3 力放大系数的仿真结果:(a) 第一级微杠杆;(b) 双级杠杆(l1=8 μm)Fig.3 Simulation results of the force amplifying factor: (a) 1st stage micro-leverage; (b) two-stage micro-leverage (l1 = 8 μm)
从图3看出,双级杠杆的力放大系数比单级杠杆的力放大系数低,这是因为多级杠杆系统降低了整个系统的弹性常数。根据力放大系数的计算公式(1)~(3),i阶杠杆在i-1阶杠杆的输出位置时,i-1阶杠杆的输出梁(连接梁)轴向刚度kvo减少,使得力放大系数和灵敏度降低。因此,需要对双杠杆系统的进行系统的参数化仿真分析,得到最优的力放大系数。最终当l1=30 μm,l2= 30 μm时,双级微杠杆的力放大系数达到最大值A=36.8。
最后仿真分析―I‖形支撑梁和普通折叠梁的敏感方向(y)和交叉方向(x)的刚度,它们的结构参数相同:总长ls=140 µm,梁宽ws=3 µm,梁厚ts=2.1 µm。仿真模型如图4所示。结果表明:―I‖形支撑梁ky=0.084 N/m,kx=6.382 N/m;折叠梁ky=0.147 N/m,kx=5.563 N/m。―I‖形支撑梁在敏感方向的刚度ky更小,交叉方向的刚度kx更大,即―I‖形支撑梁灵敏度更高,横向干扰更小。

图4 支撑梁结构:(a) ―I‖形梁;(b) 折叠梁Fig.4 Schematic view of supporting beam: (a) I-shape beam;(b) folded beam
根据之前对AlN DETF谐振器的研究结果[22],并综合考虑工艺水平、结构强度以及各性能参数相互制约等因素,AlN谐振式加速度计优化后的整体结构如图5所示,结构参数如表1所示。

表1 加速度计的结构参数Tab.1 Structure parameters of the accelerometer
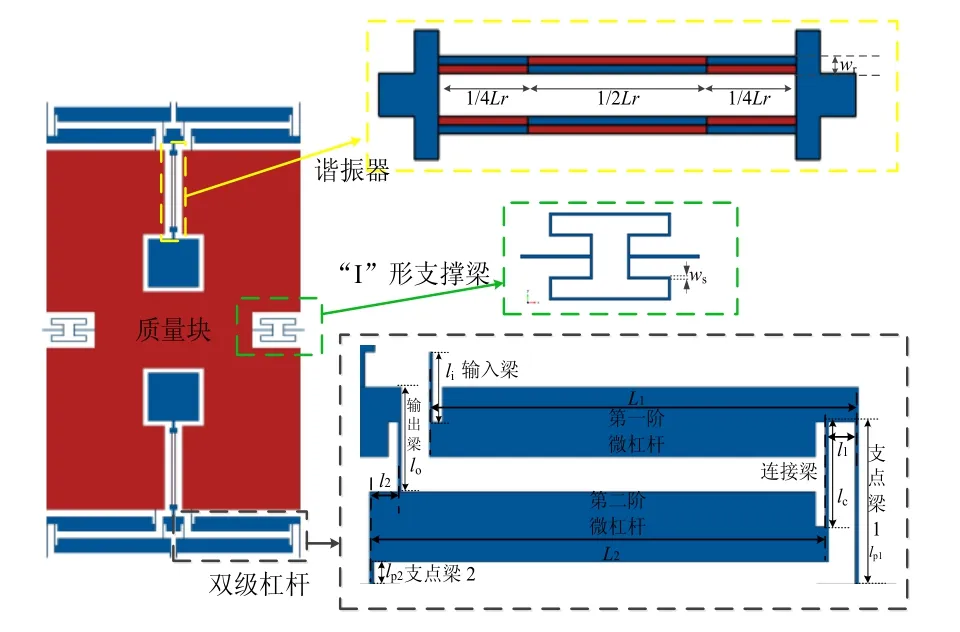
图5 加速度计优化后的整体结构Fig.5 Whole schematic after optimizing the accelerometer
2.1 预应力仿真模型
在有限元软件中建立AlN差分谐振式加速度计的预应力仿真模型,通过预应力特征频率分析可以得到谐振器谐振频率与加速度的关系,进而得到加速度计的灵敏度。预应力特征频率分析有两个计算步骤:第一步,通过稳态分析得到加速度作用下AlN谐振器的结构应力分布;第二步,将谐振器的结构应力添加到特征频率计算中,得到加速度作用下的谐振频率。
AlN谐振式加速度计的预应力仿真模型如图6(a)所示,包括质量块、―I‖形支撑梁、中心锚点、双级微杠杆、谐振器几个部分。两个谐振器通过中心锚点隔离,不仅能降低加速度计的温度灵敏度和横向干扰,还能有效地抑制两个谐振器之间的机械耦合[12]。为了缩短计算时间,对整个加速度计模型进行了简化,忽略了硅基底结构,在各锚点(可动结构与基底的连接处)上施加固定约束,限制其在各个方向上的位移。通过在谐振器的驱动电极上施加 0.5 V的交流电压,并将底电极接地,实现了AlN DETF谐振器的压电激励。当有加速度(y轴)作用时,通过预应力特征频率分析,可以得到谐振器的谐振频率,根据谐振频率差即可求出输入加速度的大小。
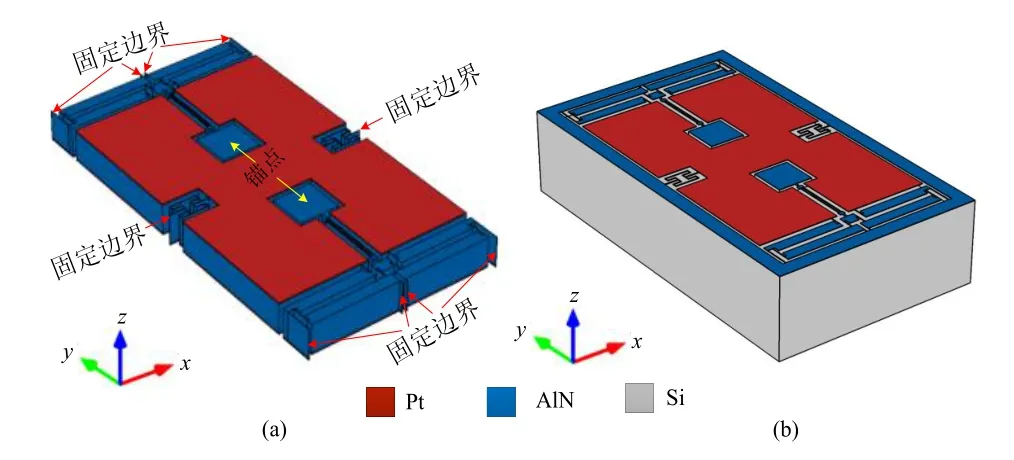
图6 多物理场仿真模型:(a) 预应力仿真模型的三维示意图;(b) 热应力仿真模型的三维示意图Fig.6 Multiphysical simulation model: (a) 3D schematic of pre-stress analysis model; (b) 3D schematic of thermal stress analysis model
2.2 热应力仿真模型
结构层的材料包括AlN和Pt,因此结构层的厚度为电极、振梁的厚度之和(2.2 µm);衬底的材料为Si,厚度为500 µm。由于结构层和衬底材料的热膨胀系数不同,随着温度变化,AlN谐振器会产生附加的拉压应力,进而引起谐振器频率漂移,因此,对AlN加速度计的整体结构进行热仿真分析在结构设计过程中起着重要的作用。在建立几何模型的时候,除了可动结构外,还要建立硅基底的结构,AlN谐振式加速度计的热应力仿真模型如图6(b)所示。在有限元仿真软件中,设定加速度计的工作温度范围为-40~60 ℃,参考温度为20 ℃。首先改变加速度计的工作温度,热仿真分析得AlN谐振器的热应力分布;之后将谐振器的热应力添加到特征频率计算中,得到热应力作用下的谐振频率。通过热仿真分析可以得到AlN谐振器的谐振频率与温度的关系,进而得到加速度计的温度灵敏度。
3 结果与讨论
3.1 模态分析
AlN DETF谐振器存在两个一阶面内模态:面内对称模态(工作模态)和面内反对称模态(干扰模态)。如果干扰模态与工作模态的谐振频率太近,则谐振器的一些振动能量会激发寄生模式,降低Q值。因此,需要对AlN差分谐振式加速度计进行模态分析,尽可能地将面内对称模态(工作模态)与干扰模态拉开。仿真结果如图7所示。

图7 加速度计的模态仿真:(a) 谐振器1的工作模态;(b)谐振器2的工作模态;(c) 谐振器1的干扰模态;(d) 谐振器2的干扰模态Fig.7 Modal simulation of the accelerometer: (a) Working mode of resonator 1; (b) Working mode of resonator 2;(c) Interferential mode of resonator 1;(d) Interferential mode of resonator 2
谐振器1的工作模态频率f1为373 259.1 Hz,谐振器2的工作模态频率f2为373 285.2 Hz。在外界加速度载荷为零的情况下,两个谐振器的尺寸完全相同,整体结构上下左右完全对称,则两个谐振器的基频应该同频振动。但是在仿真过程中,由于网格划分的不对称性,两个谐振器的谐振频率并不完全相同。谐振器1的干扰模态频率为382 567.5 Hz,谐振器2的干扰模态频率为382 699.9 Hz,干扰模态与工作模态的频率差大约为9.4 kHz,有效地实现了模态隔离。
3.2 灵敏度分析
AlN差分谐振式加速度计的量程初步设定为-40~40g,并通过稳态分析(预应力特征频率分析中的第一步)得到加速度计在40g加速度作用下的应力分布,验证该加速度计的结构强度是否满足要求。因此,在y轴正方向(加速度计的敏感方向)施加40g的加速度载荷,得到Von Mises应力分布云图如图8所示。
从图8可以看出,当施加40g的加速度时,最大应力点出现在支撑梁上,最大应力为28.9 MPa,低于材料的强度极限(AlN为400 MPa,Pt为240 MPa)。
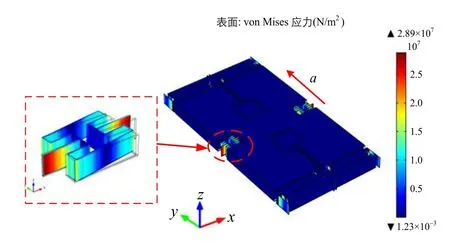
图8 加速度计的应力分布(40g)Fig.8 Stress distribution of the accelerometer under 40g
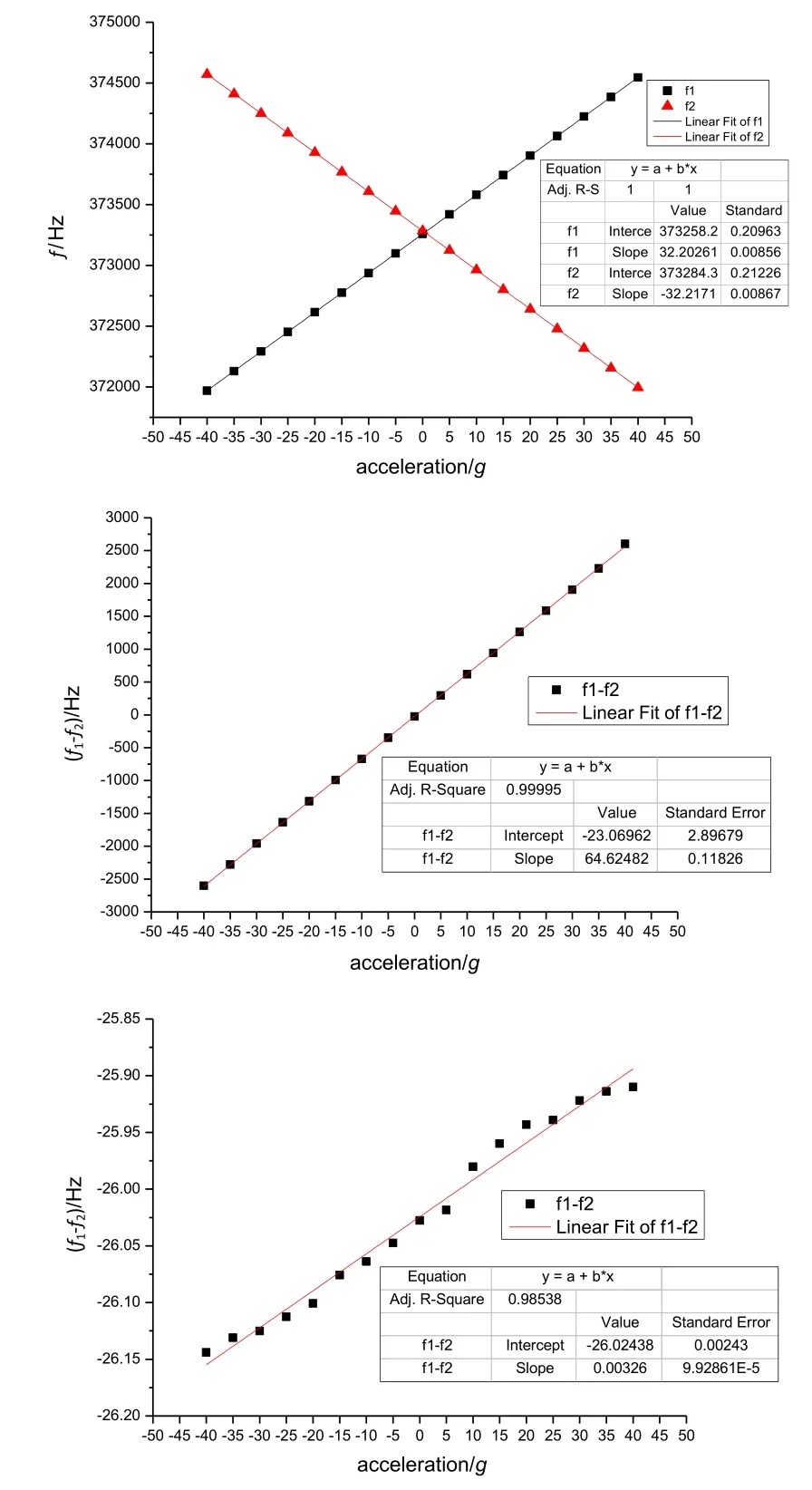
图9 灵敏度的仿真结果:(a) AlN DETF的谐振频率vs加速度;(b) 输出差频vs加速度;(c) 输出差频vs加速度(x轴)Fig.9 Simulation results of sensitivity: (a) Resonant frequency of AlN DETF versus acceleration ; (b) Differential frequency of output versus acceleration; (c) Differential frequency of output versus acceleration(x axis)
在±40g量程范围内对AlN差分谐振式加速度计进行预应力特征频率仿真,得到灵敏度的结果如图 9所示。图9(a)为AlN DETF的谐振频率与加速度的线性拟合曲线,图9(b)为输出差频与加速度的线性拟合曲线,图 9(c)为输出差频与横向加速度(x轴)的线性拟合曲线。从图9可以看出,两个谐振器的谐振频率变化趋势相反,单个谐振器的灵敏度约为 32.2 Hz/g,加速度计的灵敏度为 64.6 Hz/g,线性度为0.787%,横向灵敏度为0.0033 Hz/g。表2将本文的仿真结果与其他AlN谐振式加速度计的性能参数进行比较,结果表明本文设计的AlN差分谐振式加速度计具有更高的灵敏度,更低的横向灵敏度,这主要归功于双级微杠杆以及支撑梁结构的优化。

表2 AlN谐振式加速度计的性能对比Tab.2 Performance comparison of AlN resonant accelerometer
3.3 热仿真分析
为了评估AlN差分谐振式加速度计承受高温热应力的能力,根据图6(b)的热应力仿真模型,得到加速度计在150 ℃高温下的热应力分布,如图10所示。整个加速度计最大热应力出现在振梁两端顶电极与氮化铝的界面处,最大值为164 MPa,低于各材料的强度极限。结果表明,AlN谐振式加速度计能够承受150 ℃高温产生的热应力。
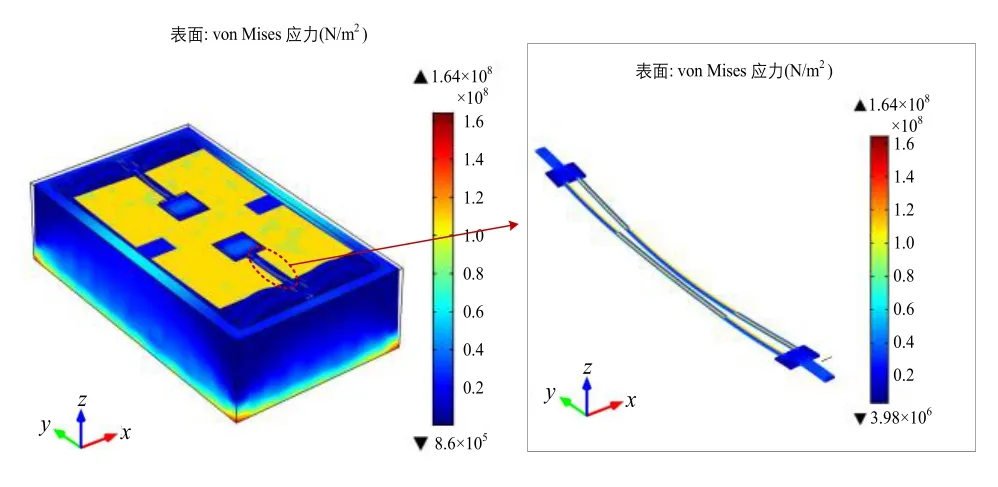
图10 加速度计的热应力分布(150 ℃)Fig.10 Stress distribution of the device at high temperature (150 ℃)
将仿真温度设为实际工作的温度范围(-40~60℃),温度间隔为5℃,参考温度为20℃。热应力仿真的结果如图11所示,图11(a)为AlN DETF的谐振频率与温度的线性拟合曲线,图11(b)为输出差频与温度的线性拟合曲线。从图 11可以看出,两个 AlN谐振器的谐振频率随温度的升高而增大,单个谐振器的温度灵敏度约为490 Hz/℃,加速度计输出差频的温度灵敏度为-0.83Hz/℃。输出差频的温度灵敏度远小于单个谐振器的温度灵敏度,验证了差频检测方案能够降低温度共模误差。
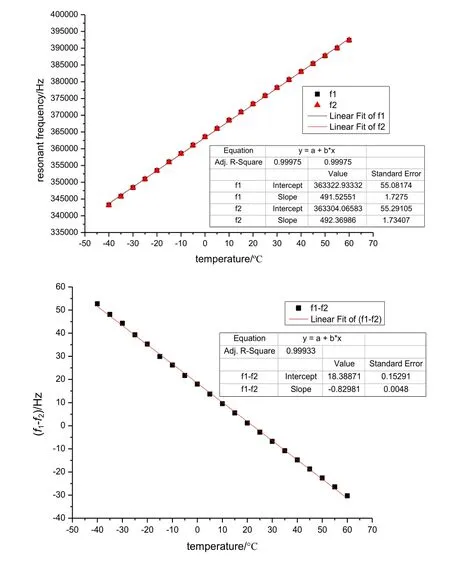
图11 热应力的仿真结果:(a) AlN DETF的谐振频率vs温度;(b) 输出差频vs温度Fig.11 Simulation results of thermal stress: (a) Resonant frequency of AlN DETF versus temperature; (b) Differential frequency of output versus temperature
4 结 论
设计并仿真分析了一种AlN差分谐振式加速度计。通过引入两级微杠杆来放大质量块的惯性力,提高了灵敏度;采用一种―I‖形结构的支撑梁来降低横向灵敏度;利用差频检测方案降低温度共模误差的影响。该加速度计主要由质量块、支撑梁、双级微杠杆和谐振器组成,并通过理论分析和有限元仿真优化了它们的结构参数。模态分析表明,两个谐振器工作模态与干扰模态的频率差大约为9.4 kHz,有效地实现了模态隔离。根据灵敏度的仿真结果,加速度计的灵敏度为64.6 Hz/g,线性度为0.787%,横向灵敏度为0.0033 Hz/g。与之前报道的AlN谐振式加速度计相比,所提出的加速度计具有更高的灵敏度以及更低的横向干扰,这主要归功于双级微杠杆系统以及支撑梁结构的优化。
热应力的仿真结果表明,该加速度计能够承受150 ℃高温产生的热应力,并且在-40~60 ℃范围内,单个谐振器的温度灵敏度约为490 Hz/℃,输出差频的温度灵敏度为-0.83 Hz/℃,验证了差频检测方案能够降低温度共模误差的影响。
参考文献(References):
[1]高杨, 雷强, 赵俊武, 等. 微机械谐振式加速度计的研究现状及发展趋势[J]. 强激光与粒子束, 2017, 29(8): 1-14.
[2]Jing Z, Yan S, Qin S, et al. Microelectromechanical resonant accelerometer designed with a high sensitivity[J].Sensors, 2015, 15(12): 293-310.
[3]Park U, Rhim J, Jeon J U, et al. A micromachined differential resonant accelerometer based on robust structural design[J]. Microelectronic Engineering, 2014, 129(16): 5-11.
[4]Xia G M, Qiu A P, Shi Q, et al. Test and evaluation of a silicon resonant accelerometer implemented in SOI technology[C]//IEEE Sensors. 2013: 1-4.
[5]Yang B, Wang X, Dai B, et al. A new Z-axis resonant micro-accelerometer based on electrostatic stiffness[J].Sensors, 2015, 15(1): 687-702.
[6]Wung T S, Ning Y T, Chang K H, et al. Vertical-plate-type microaccelerometer with high linearity and low cross-axis sensitivity[J]. Sensors & Actuators A: Physical, 2015, 222(1): 284-292.
[7]Li C, Zhao Y, Li B, et al. A micro-machined differential resonance accelerometer based on silicon on quartz method[J].Sensors & Actuators A Physical, 2017, 253(1): 1-9.
[8]Wang Y, Ding H, Le X, et al. A MEMS piezoelectric in-plane resonant accelerometer based on aluminum nitride with two-stage microleverage mechanism[J]. Sensors &Actuators A Physical, 2017, 254(1): 126-133.
[9]Caspani A, Comi C, Corigliano A, et al. A differential resonant micro accelerometer for out-of-plane measurements ☆[J]. Procedia Engineering, 2014, 87(1): 640-643.
[10]Li B, Zhao Y, Li C, et al. A differential resonant accelerometer with low cross-interference and temperature drift[J]. Sensors, 2017, 17(1): 178.
[11]Vigevani G, Przybyla R J, Yen T T, et al. Characterization of a single port aluminum nitride tuning fork[C]// IEEE International Ultrasonics Symposium. 2010: 1281-1285.
[12]Vigevani G. MEMS aluminum nitride technology for inertial sensors[D]. Berkeley: University of California, 2011.
[13]Olssoniii R H, Wojciechowski K E, Baker M S, et al.Post-CMOS-compatible aluminum nitride resonant MEMS accelerometers[J]. Journal of Microelectromechanical Systems,2009, 18(3): 671-678.
[14]Vigevani G, Goericke F T, Pisano A P, et al. Microleverage DETF Aluminum Nitride resonating accelerometer[C]//IEEE Frequency Control Symposium. 2012: 1-4.
[15]Caspani A, Comi C, Corigliano A, et al. Compact biaxial micromachined resonant accelerometer[J]. Journal of Micromechanics & Microengineering, 2013, 23(10): 10-16.
[16]Shin D D, Ahn C H, Chen Y, et al. Environmentally robust differential resonant accelerometer in a wafer-scale encapsulation process[C]//IEEE International Conference on MICRO Electro Mechanical Systems. 2017: 17-20.
[17]Zou X, Thiruvenkatanathan P, Seshia A A. A Seismicgrade resonant MEMS accelerometer[J]. Journal of Microelectromechanical Systems, 2014, 23(4): 768-770.
[18]Su S X P, Yang H S, Agogino A M. A resonant accelerometer with two-stage microleverage mechanisms fabricated by SOI-MEMS technology[J]. IEEE Sensors Journal,2005, 5(6): 1214-1223.
[19]Ding H, Zhao J, Xie J. A novel biaxial resonant micro accelerometer with microleverage mechanism[C]//IEEE International Conference on Nano/micro Engineered and Molecular Systems. 2015: 50-53.
[20]Vigevani G, Goericke F T, Izyumin I I, et al. Electrode design and coupling optimization of Aluminum Nitride DETF[C]//IEEE Ultrasonics Symposium. 2011: 1731-1734.
[21]Ding H, Zhao J, Ju B F, et al. A high-sensitivity biaxial resonant accelerometer with two-stage microleverage mechanisms[J]. Journal of Micromechanics & Microengineering, 2016, 26(1): 1-11.
[22]Lei Q, Gao Y, Han C, et al. Structure design of aluminium nitride double-ended tuning fork resonators[J]. High Power Laser and Particle Beams, 2017, 29(10): 1-5.

