从车轮磨耗谈动车组异常振动

惠鹏举

(武汉铁路局 武汉动车段， 武汉 430080)

车轮磨耗引起车轮踏面形状改变，从而导致轮径差和等效锥度发生较大变化，最终影响车辆的动力学性能。由于动车组运行速度高，加剧了车轮的磨耗，使得车辆稳定性、安全性以及轮轨使用寿命都受到很大影响。踏面形状异常引起的动车组异常振动现象时有发生，对动车组的运营安全造成很大困扰，如何正确认知需要开展深层次的研究。

1 车轮踏面等效锥度

1.1 等效锥度的计算

锥形踏面车轮滚动圆附近为斜率固定的直线段，在直线段范围内车轮踏面锥度为常数。车轮踏面磨耗后，滚动圆附近一般不是直线段，这时计算车轮踏面外形锥度需要采用其等效值，即等效锥度。

等效锥度的实质是非锥形踏面轮对在每一横移幅值下均等效于一个锥形踏面轮对，其等效的依据是两者的运动轨迹波长相等。根据Klingel公式可以计算出这一运动轨迹的波长，即：

(1)

式中λe为对运动轨迹(正弦波)的波长；b为左右轮轨接触点距离的一半；r0为滚动圆半径；γ为轮踏面的锥度角。

应用Klingel公式计算等效锥度：

(2)

1.2 等效锥度对车辆稳定性的影响

车辆在直线轨道上运行时，由于车轮踏面及轮缘与钢轨接触点不同，轮对中心和线路中心会有一定的偏差，使得车辆同一车轴上的左右车轮滚动直径和滚动距离不同。此时，车轮向前滚动时既做摇摆运动，又做摇头运动，其轮对中心轨迹呈波浪形(如图1所示)，称为

蛇行运动。蛇行运动是一种自激振动，是轮对对钢轨的相对运动产生了内部激振力，由这种激振力维持轮对相对运动。

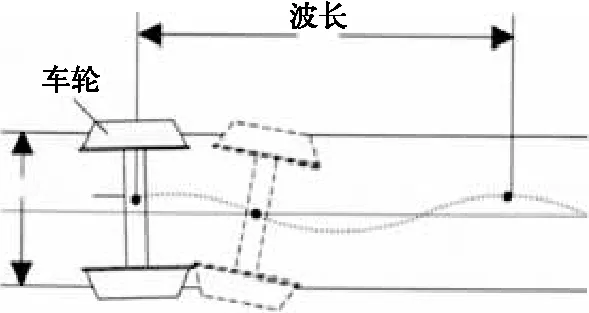
图1 轮对的蛇行运动

根据Klingel公式，车轮的蛇行运动频率与踏面等效锥度满足如下关系：

(3)

可以看出，踏面等效锥度越大，车轮的蛇行运动频率也越大。

因此，蛇行运动频率随速度和等效锥度的增大而增大。车轮磨耗后，引起踏面形状变化，造成等效锥度增大，增强了轮轨横向作用力，增大了轮对横向振动，而车体固有频率相对较低，且稳定不变，只要车辆开始运行，蛇行频率与车体固有频率重合几乎不可避免，车体共振必然会发生。当车体共振发生在高速区段时，这种共振会导致车辆平稳性和舒适度严重恶化。

2 车轮多边形

2.1 测试方法

如图2(a)、(b)所示。测试时使用千斤顶将同轴两侧轴箱抬起，使车轮垂直脱离轨面1～3 mm可自由转动，测试设备固定于钢轨上方，传感器1位于车轮踏面名义滚动圆处，用于记录车轮多边形信息。传感器2用于测量车轮的周长信息。

图2 车轮多边形测试

车轮多边形由踏面滚动圆位置对应的径向变动量随相位的函数(简称：径跳函数)及其傅里叶变换参数来评价，1-9阶称为低阶多边形，10阶及以上称为高阶多边形。为方便观察车轮的多边形情况，通常在极坐标中表示，如图3所示。

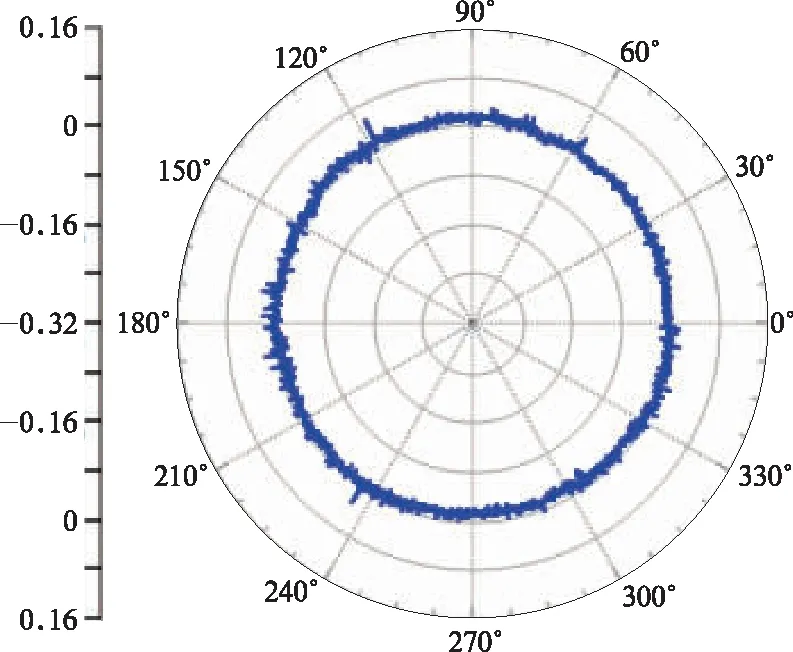
图3 极坐标显示图

车轮多边形参数计算过程为：

(1)径跳函数去毛刺和曲率滤波处理；

(2)对一个周期的径跳函数采用离散傅里叶变换计算径跳函数的频谱。得到各阶次对应的有效值Ai；

(3)采用相对0.001 mm的对数评估幅值大小，计算公式为： 20×log(Ai/0.001) dB，故此若Ai=0.001 mm，对应0 dB，若Ai=0.01 mm，对应20 dB。

2.2 车轮多边形对车辆稳定性的影响

车轮多边形会引起车辆系统振动频率的变化，引起的振动频率f为：

f=(n·v)/(2π·r0)

(4)

式中v为车辆运行速度，km/h；n为车轮多边形阶数；r0为车轮滚动圆半径。

可以看出，车轮多边形引起的振动频率与车辆运行速度、车轮多边形阶数呈线性关系。

转向架构架的弹性振动频率较低，车轮低阶多边形引起的振动频率与其接近，容易发生共振。车轮高阶多边形引起的振动频率较高，经二系悬挂系统的衰减，对转向架构架垂向振动加速度的影响反而不大。同理，车体垂向振动加速度受车轮低阶多边形影响较大，而对高阶多边形不敏感。

车辆运行平稳性分别按平稳性指标和平均最大振动加速度评定。平稳性指标计算如式(5)

(5)

式中W为平稳性指标；A为振动加速度，g；f为振动频率，Hz；F(f)为频率修正系数(垂直振动频率20 Hz以上时，F(f)=1)。

可以看出，车辆平稳性指标随着振动加速度的增大而增大，但是频率在20 Hz以上的振动对平稳性指标的影响很小。

车轮多边形引起的振动，主要影响车辆系统的垂向振动，且在高速条件下多边形引起的轮轨周期性振动频率较高，超出了平稳性指标的敏感范围，因此，车轮多边形阶数对平稳性指标几乎没有影响。车轮多边形对低速下的垂向平稳性指标影响较大，主要是因为低速运行下车轮多边形引起的振动频率更低。

3 动车组异常振动分析

某动车组正线运营，当车速在140～160 km/h时，6车2位端车下有异常振动，当车速低于100 km/h时，异常振动消失。对轮对、轴箱、制动夹钳、转向架构架以及附属配件检查未发现异常，对车轮轮辋轮辐探伤，检测结果正常。需要对车轮磨耗进行测量，计算车轮等效锥度及多边形，分析振动原因。

3.1 车轮等效锥度测试

对某动车组车轮踏面进行测量，如图4～图13所示。

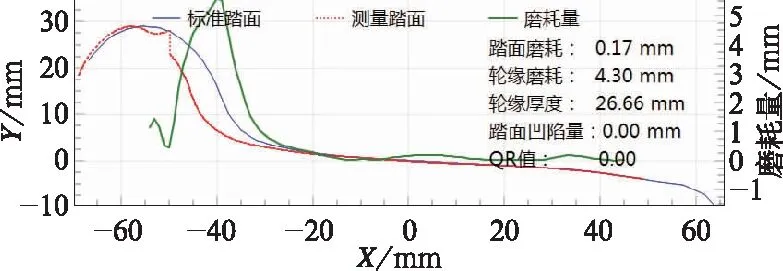
图4 6车5位车轮踏面测量曲线

图5 6车6位车轮踏面测量曲线

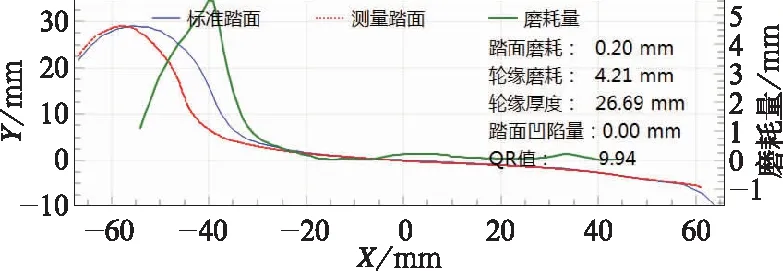
图6 6车7位车轮踏面测量曲线

图7 6车8位车轮踏面测量曲线

数据处理见表1～表2。

3、4位轮对车轮磨耗后，轮径差较小(小于1 mm)，引起的等效锥度变化小，且与整车平均等效锥度(0.105)接近，但远高于名义等效锥度(UIC519定义名义等效锥度是指在轮对蛇行运动幅值为3 mm时所对应的等效锥度，λN=0.057)，小于等效锥度限值(v≤200 km/h，等效锥度限值为0.40)，对蛇行稳定性有一定的影响。车轮磨耗后，轮轨接触点分布较宽，且比较均匀，对车辆的蛇行稳定性影响不大。

图8 6车3位轮对轮轨关系

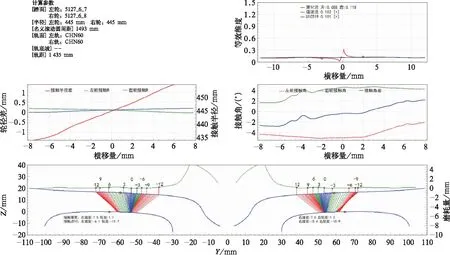
图9 6车4位轮对轮轨关系

轮位滚动圆磨耗/mm测量值均值轮缘磨耗/mm测量值均值踏面凹陷量/mm位置磨耗量最大磨耗量/mm位置磨耗量轮缘厚度/mmQR值6-3-50.170.174.304.309.890.00-190.2326.660.006-3-60.120.124.394.399.990.00-190.1626.4510.106-4-70.20.24.214.219.860.0030.2326.699.946-4-80.030.034.254.259.950.00420.1726.6410.06

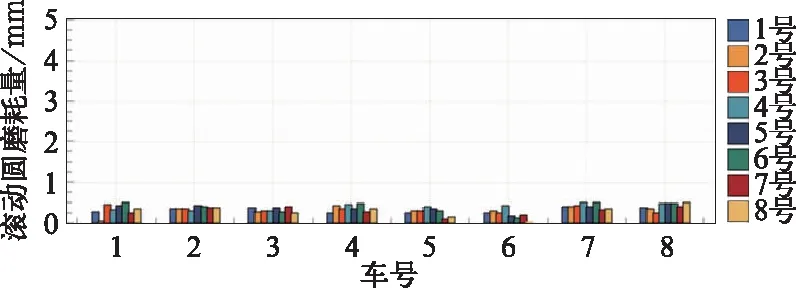
图10 各车滚动圆磨耗量

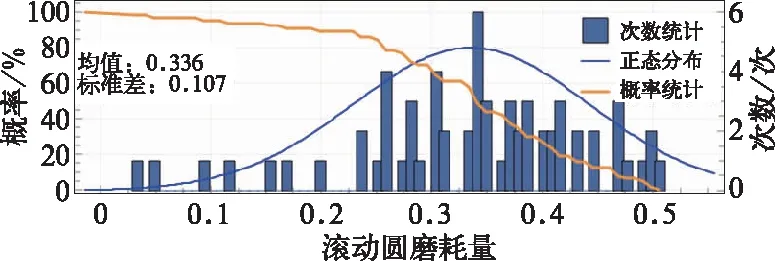
图11 各车滚动圆磨耗分布

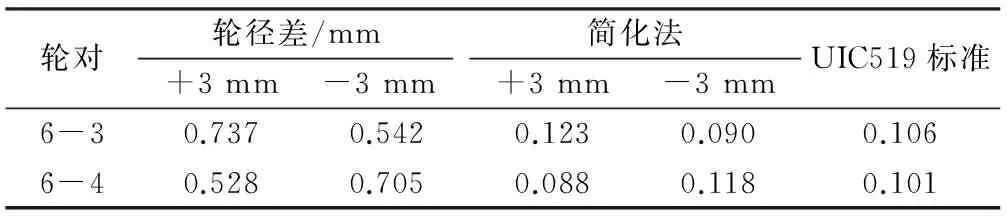
轮对轮径差/mm+3mm-3mm简化法+3mm-3mmUIC519标准6-30.7370.5420.1230.0900.1066-40.5280.7050.0880.1180.101

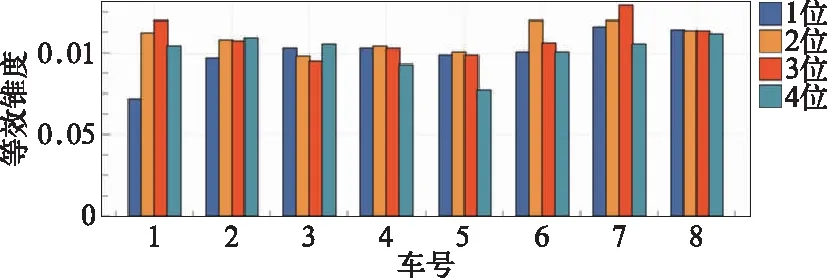
图12 各车等效锥度(UIC519标准)

图13 各车等效锥度分布

3.2 车轮多边形测试

图14(a)、(b)，图15(a)、(b)记录了车轮的多边形测试结果。

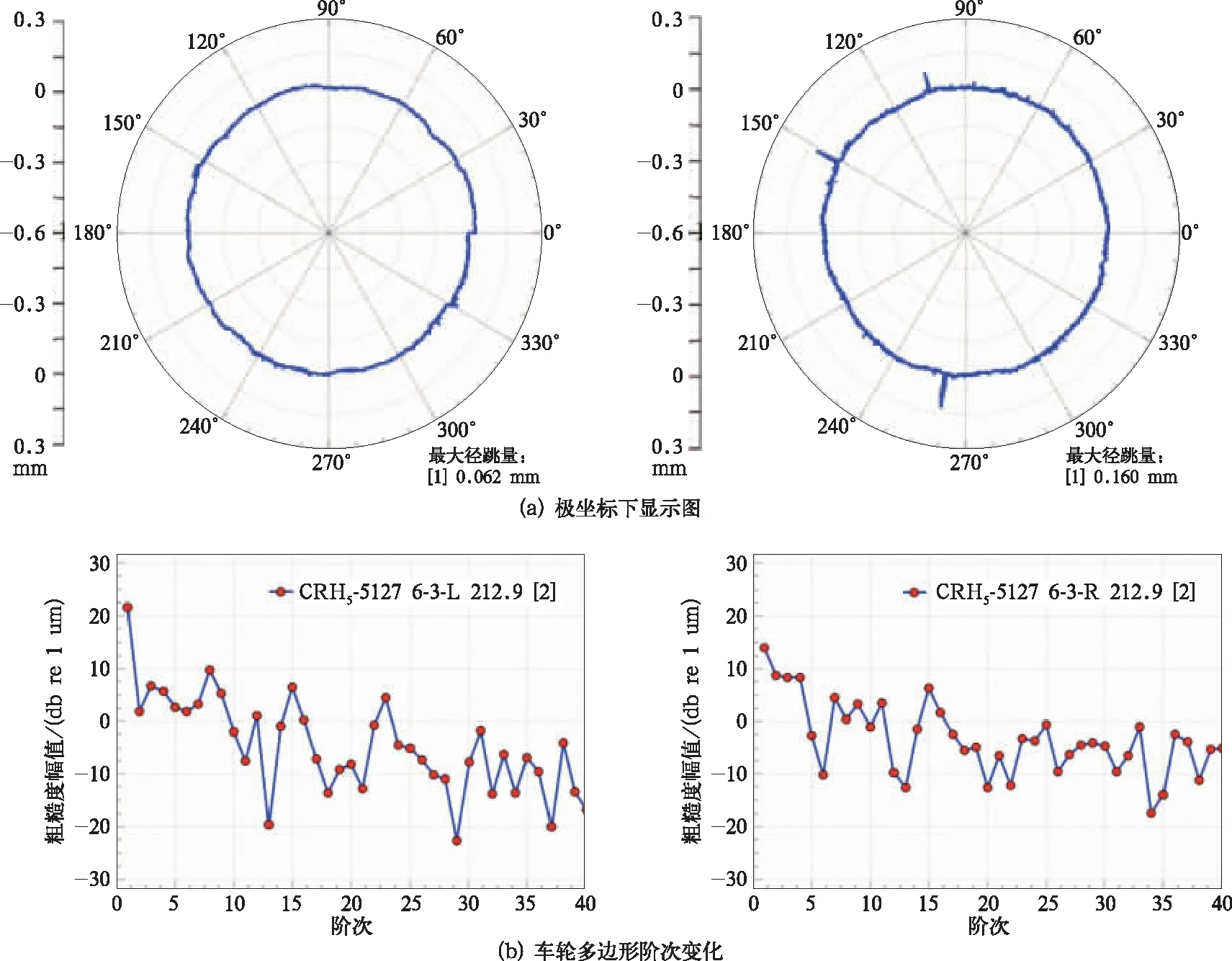
图14 5、6位车轮多边形测试结果

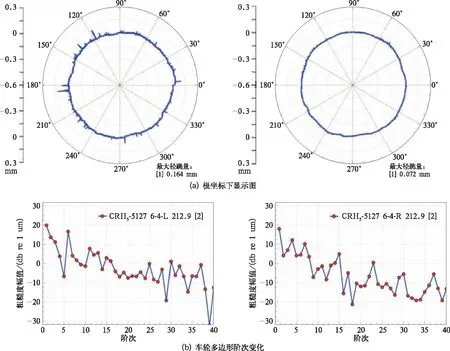
图15 7、8位车轮多边形测试结果

数据处理见表3。

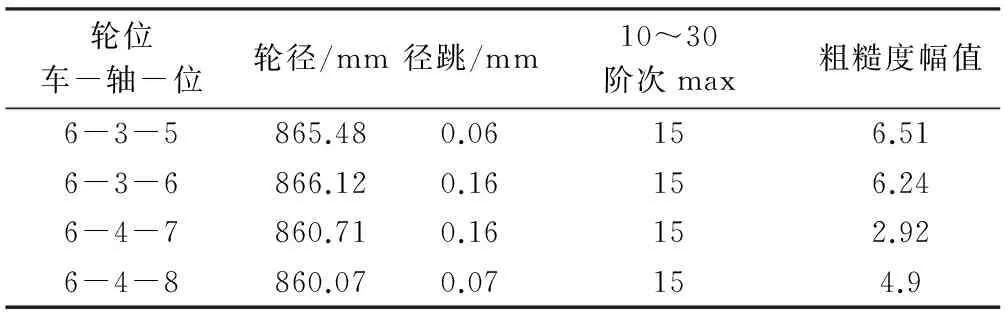
表3 动车组旋修前车轮多边形统计表

4个车轮径跳之小于0.2 mm，其中6、7位车轮径跳值介于0.1～0.2 mm，5、6位车轮径跳值小于0.1 mm。5、6、8位车轮磨耗后，10～30阶次粗糙度幅值均小于14 dB，没有高阶多边形显著，表现为偏心(1阶)；7位车轮存在六边形，粗糙度幅值为16.67 dB/μm，车轮多边形轻微。

计算运行速度在100，120，140，160，200 km/h时车轮多边形引起的振动频率(表4)，在车辆速度为140～160 km/h时，5、6、8位车轮偏心引起的振动频率在14.3～16.5 Hz之间，7位车轮六边形引起的振动频率在86.3～98.7 Hz之间。

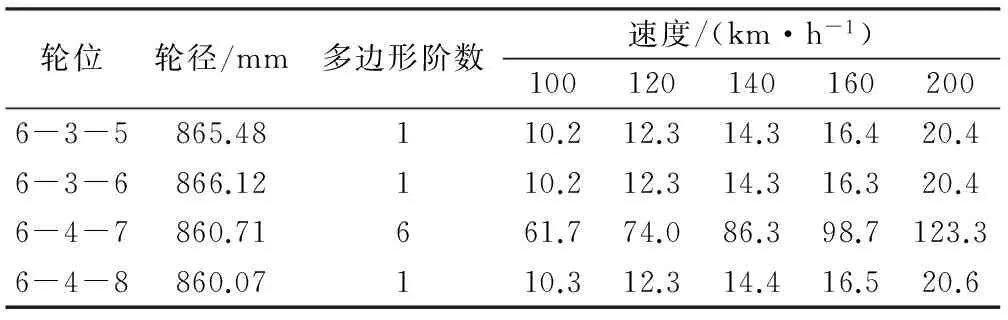
表4 动车组旋修前车轮多边形引起的振动频率 Hz

3.3 动车组平稳性测试

使用RCV-1型铁道车辆舒适度仪，在6车2位端车厢内地板处测试平稳性，结果如图16、图17所示。

图16 车体平稳性指标

测试结果：

(1)横向平稳性指标最大为2.241，且仅有极少数超过2.0，但未超过2.5，达到1级标准(GB 5599-85)；垂向平稳性指标最大为2.011，除有1次超过2.0，其余均小于2.0，达到1级标准(GB 5599-85)。

图17 车体振动加速度

(2)车体横向振动加速度在±0.2g范围内，垂向振动加速度在±0.2g范围内，小于2.5 m/s2。车体垂向振动加速度大于横向振动加速度。

基于前述分析，在车辆速度为140～160 km/h的高速情况下，6车7位车轮多边形引起的振动频率较高，超出了平稳性指标的敏感范围，对垂向平稳性指标几乎没有影响。

4 结 论

(1)蛇行运动频率随速度和等效锥度的增大而增大，只要车辆开始运行，蛇行频率与车体固有频率重合导致车体发生共振，影响车辆的平稳性和舒适度。

(2)车轮多边形引起的振动频率一般较高，主要影响车辆系统的垂向振动，且在高速条件下多边形引起的轮轨周期性振动频率较高，超出了平稳性指标的敏感范

围，因此，车轮多边形阶数对平稳性指标几乎没有影响。车轮多边形对低速下的垂向平稳性指标影响较大，主要是因为低速运行下车轮多边形引起的振动频率更低容易与构架的弹性振动频率发生共振。

(3)故障动车组车轮存在6阶多边形，是引起动车组发生异常振动现象的原因。当动车运行速度为140～160 km/h时，车轮多边形引起的低频振动，与转向架构架的弹性振动发生共振，导致低频振动加剧，引起车辆垂向振动变化，但因振动频率在20 Hz以上，对车体的平稳性指标的影响很小。

[1] 吴 宁,董孝卿,林凤涛,等.等效锥度的计算及验证[J]. 铁道机车车辆,2013,33(1):49-52.

[2] 李 艳,张卫华,池茂儒,等.车轮踏面外形及轮径差对车辆动力学系能的影响[J]. 铁道学报, 2010, 32(1):104-108.

[3] 池茂儒,张卫华,曾 京,等.轮径差对车辆系统稳定性的影响[J].中国铁道科学, 2008, 26(6): 65-69.

[4] International Union of Railways．UIC 518：2003Testing and approval of railway vehicles from point ofview of their dynamic behavior-Safety-Track fatigue-Ride quality[S]．

[5] 张雪珊,肖新标,金学松.高速车轮椭圆化问题及其对车辆横向稳定性的影响[J].机械工程学报,2008,44(3):50-57.

[6] 王 伟,曾 京,罗 仁. 列车车轮不圆顺的研究现状[J]. 国外铁道车辆, 2009, 46(1): 39-43.

[7] Anders Johansson.Out-of-round railway wheels-assessment of wheel tread irregularities in train traffic[J]. Journal of Sound and Vibration. 2006, (293)： 795-806.