虚拟同步发电机的并网功率控制及模式平滑切换
颜湘武, 贾焦心, 王德胜, 李正文, 葛延峰
(1. 河北省分布式储能与微网重点实验室(华北电力大学), 河北省保定市 071003;2. 国网辽宁省电力有限公司, 辽宁省沈阳市 110006)
0 引言
由于清洁能源在很长一段时期内仍需要接入同步电网,因此虚拟同步发电机(virtual synchronous generator,VSG)技术应运而生,并且近年来受到了广泛关注。采用VSG技术的分布式电源具备与同步机组相同的运行机制,都能自主地参与电网的运行和管理,并在电网电压/频率、有功功率/无功功率异常情况下做出相应的响应,积极应对电网的暂态和动态稳定问题[1-2]。
文献[3-8]研究了VSG技术在风电、光伏、储能等不同场景下的应用问题,每种场景都会有并网和离网运行工况。对于双模式运行的VSG,需要保证储能单元的荷电状态(state of charge,SOC)在充放电过程中都在安全范围内,一旦由于VSG直流侧的分布式电源功率波动或VSG参与一次调频导致储能单元SOC超出安全范围,则需停止放电或充电[9]。此时,若依旧采用VSG控制策略,则直流侧的分布式电源由于需要预留容量而无法实现最大功率控制[1]。此外,文献[6]指出当电网频率与储能VSG频率额定值之间的偏差较大时,常规VSG控制策略由于具有频率和电压下垂特性(本文称为下垂控制模式,即Droop控制模式),需要吸收或者发出大量有功功率才能与电网频率达成平衡,这可能导致储能VSG过载。因此,仅仅依靠VSG的频率下垂控制不能适应并网运行,有必要研究能够与VSG的Droop控制模式平滑切换的PQ控制(恒功率控制)模式。
VSG输出有功功率的动态和稳态特性由虚拟惯量和阻尼系数的大小决定,难以兼具良好的动态和稳态性能。为此,一些学者提出了改进的控制策略,主要包括:基于微分补偿环节虚拟惯量的方法[10]、自适应虚拟惯量的VSG控制算法[11-12]。改进后的控制策略可以提高VSG控制性能,但在电网频率发生波动时仍无法实现并网工况的恒功率控制。此外,虚拟阻抗方法也可以调节VSG的动态性能[7],但输出阻抗相对于动态响应与均流的控制规律相矛盾,也存在难以兼顾的问题。
为实现电网频率扰动下VSG的恒功率控制,目前主要的策略为:在VSG功率环中增加比例—积分(PI)调节器[13];增加切换策略,将并网的逆变微源切换成PQ控制[6];将实时测量的电网频率作为VSG的频率参考[14];通过上层控制系统进行二次调节[15]。
文献[13]通过增加PI调节器进行有功功率的闭环控制,进而可以实现并网稳态下VSG恒功率控制,但该方法增加了功率环的阶次,影响VSG原有的优越惯性和阻尼性能。文献[6]通过PQ控制与VSG控制之间的协调控制来提升并网性能,孤岛时采用VSG控制,并网时采用PQ控制,采用该方案时逆变微源无法为电网提供惯量和阻尼支撑,并且该方案增加了被动并网和离网切换难度。文献[14]将实时测量的电网频率作为VSG的频率参考值,可以实现并网稳态下VSG恒功率控制。但是,用于测量频率的锁相环存在非线性、响应慢、参数设计难等问题[2],需要进一步研究。
综上所述,现有控制策略难以同时实现并网运行VSG的恒功率控制与惯量、阻尼支撑相互协调。本文对比分析VSG功率环模型与基于虚拟功率的锁相环模型,提出将功率环模型校正为有零点典型二阶系统。校正后的功率环不仅具有同步机制和提供惯性功率支撑的能力,而且可以实现电网频率扰动下恒定稳态有功功率的控制。
1 VSG原理
VSG并网的主电路结构与同步发电机存在对偶关系,其物理等效关系为:将分布式电源及储能单元等效为原动机;逆变电路和电感—电容(LC)滤波器等效为发电机;逆变桥臂中点电压等效为发电机的内电势;输出电压(即滤波电容电压)等效为发电机的输出端电压;滤波电感等效为发电机的同步电感;滤波电感的电阻等效为发电机的电枢电阻。
基于对偶关系,通过控制策略的设计,使VSG可具有同步发电机的内部机制与外特性。一种VSG方案参见图1[5,7],控制部分主要包括:比例—谐振(PR)控制器、VSG电磁方程、无功和电压调节环、有功和频率调节环、空间矢量脉宽调制(space vector pulse width modulation,SVPWM)环节。
图1中:Dp和kv为下垂系数;J为虚拟惯量;kq为无功积分系数;ωs为电网额定角频率;U为VSG输出端电压有效值;UN为VSG并网点额定电压有效值;Pref和Qref为功率给定值;Pe和Qe为VSG的电磁功率;L为VSG的滤波电感(同时也是VSG的等效输出电感);R为VSG的等效输出电阻;C为VSG的滤波电容;E0为VSG空载电势有效值;E为VSG内电势有效值;φ为VSG内电势的相位角;δ为VSG的功角(即三相内电势eabc与三相输出端电压uabc的相角差);iabc为VSG的三相输出电流;irefabc为三相输出电流参考值;ugabc为电网三相电压;Ug为并网点电压有效值;Lg为电网等效电感。

图1 VSG的控制策略Fig.1 Control scheme of VSG
2 PQ控制模式及其切换方法
2.1 PQ控制模式的提出
2.1.1Droop控制模式的功率环模型
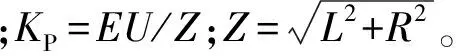

图2 Droop模式下VSG的功率环模型Fig.2 Model of power loop in VSG with droop mode
Droop模式下,VSG有功功率输入的开环传递函数为式(1),闭环传递函数为式(2)。
(1)
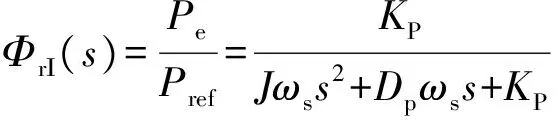
(2)
2.1.2基于虚拟有功功率的锁相环与功率环模型对比
文献[2,16]提出了基于虚拟电流或虚拟功率的VSG预同步方法,简化了VSG的预同步控制。文献[17]通过同步机数学模型设计了改进型锁相环,充分证明了同步机和虚拟同步机具有类似的同步机制。文献[18]介绍了一种基于虚拟无功功率的锁相环。上述文献的共同特点是通过虚拟功率的反馈间接实现相位同步跟踪。
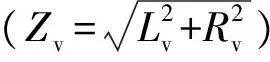
(3)
式中:Δφl为uabc与Pv-PLL电压elabc的相角差;αv为虚拟阻抗角;El为Pv-PLL电压elabc的有效值。
由式(3)可知,通过反馈Pv作为锁相环的输入可实现锁相环输出相位φl的调节。若αv≠π/2,在El=U时可实现uabc相位的无差跟踪;若αv=π/2,在El≠U时也可实现相位的无差跟踪。
线性化后可得到Pv-PLL模型,如附录A图A2所示,其中,KPv=ElU/Zv。虚拟有功功率输入的开环传递函数为式(4),闭环传递函数为式(5)。
(4)

(5)
式中:kpl和kil分别为锁相环PI调节器的比例系数和积分系数;Pvref为Pv参考值。
由式(1)可知,GrI(s)在自动控制原理中为典型Ⅰ型系统;由式(4)可知,GvrΠ(s)为典型Ⅱ型系统。因而Pv-PLL模型的稳态性能优于Droop模式功率环模型。
由式(2)可知,ΦrI(s)为无零点典型二阶系统;由式(5)可知,ΦvrΠ(s)为有零点典型二阶系统。无零点二阶系统的性能分析较为简单,而零点对二阶系统的影响则比较复杂,文献[19]分析了零点对二阶系统动态响应性能的影响,表明多数情况下零点的存在会恶化性能。
通过上述对比,主要考虑Pv-PLL模型的稳态性能,本文提出将VSG功率环模型校正为Ⅱ型系统,可得到一种基于PQ控制模式的VSG,目的是提高VSG并网运行的稳态性能。校正后的VSG功率环模型与Pv-PLL模型具有相同的结构,仍然具有同步机制,后面将具体分析。
2.2 PQ控制模式的实现及其切换方法
PQ控制模式实现方法如下:将VSG控制算法中的惯性环节替换为PI调节器环节,VSG可以实现电网频率扰动下有功功率给定值的无差跟踪;再将无功和电压调节环中的无功调节环闭合,VSG可以实现无功功率给定值的无差跟踪。
具体的功率环控制框图如图3所示,在图1的基础上加入了1个PI调节器环节、7个开关(S1至S7)以及1个预同步单元。图3中:Dvp和Jv为PI调节器参数;kvi为电压积分系数;ΔT和Δω1分别为惯性环节的输入和输出;Δω2为PI调节器环节输出;ΔE和Δωsyn分别为预同步单元输出的电压幅值和角频率调节量;ω为φ的微分量。当S1闭合,S2,S3,S4,S5断开时,VSG工作在Droop模式;当S1断开,S2,S3,S4,S5闭合时,VSG工作在PQ模式。选取Dvp=Dp,目的是实现控制模式的平滑切换。

图3 改进的VSG功率环控制框图Fig.3 Control block of improved power loop in VSG
考虑到VSG有3种运行模式,即并网模式、离网模式和预同步模式,通过组合这3种运行模式和2种控制模式可以得到5种有效的VSG模式,具体为:并网Droop模式、并网PQ模式、离网PQ模式、离网Droop模式和预同步Droop模式。此外,为了实现PQ模式的主动离网切换,增加了一种过渡模式——预离网Droop模式。
图4为6种模式切换流程图。切换流程如下。
1)首先,离网Droop模式的VSG收到并网指令后,预同步单元使能,闭合S6和S7,进入预同步Droop模式。
2)检测到预同步完成后发送并网开关合闸指令,同时断开S6和S7。
3)检测到并网开关合闸后预同步单元去使能,并复位预同步单元的PI调节器和积分调节器,ΔE和Δωsyn变为0,进入并网Droop模式。
4)断开S1,闭合S2,S3,S4,S5,VSG进入并网PQ模式;闭合S1,断开S2,S3,S4,S5,并复位PI环节的积分调节器和无功调节环的积分调节器,VSG再次进入并网Droop模式(并网Droop模式与并网PQ模式的切换条件视具体的控制策略而定)。
5)并网PQ模式的主动离网切换:收到离网指令后,闭合S1,断开S2和S4,将并网PQ模式切换为预离网Droop模式;发送并网开关分闸指令;检测到并网开关断开后,断开S3和S5,并复位PI调节器环节的积分调节器和无功调节环的积分调节器,VSG进入离网Droop模式。
6)并网Droop模式的主动离网切换:收到离网指令后直接发送并网开关分闸指令,并网开关断开后进入离网Droop模式。
7)若出现并网PQ模式被动离网的情况,则在检测到并网开关断开后,迅速将已经被动进入离网PQ模式的VSG切换为离网Droop模式。
8)并网Droop模式的被动离网切换自动进行。
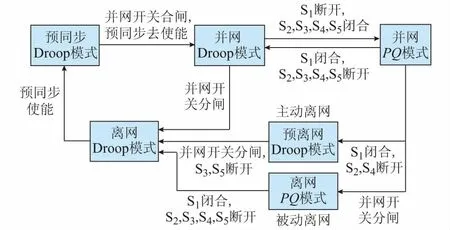
图4 运行和控制模式切换流程图Fig.4 Flow chart of switchover between operation and control modes
关于预离网Droop模式,作如下说明:对于要求VSG采用PQ模式并网运行的情形,在电网电压幅值或频率发生波动时(例如电网频率小于额定值),若并网PQ模式的主动离网切换流程是先转换到Droop模式再由Droop模式离网(此时会使得输出功率增加),则可以实现并离网平滑切换但无法满足功率控制的要求。若并网PQ模式的主动离网切换经由上述的切换流程5实现,则考虑到并网PQ模式切换为预离网Droop模式后PI调节器环节和无功调节环中积分调节器的输出值保持不变,与切换前一瞬间的值相同,并且在主动离网切换的较短时间内电网电压波动很小,因而可以基本满足功率控制的要求。
3 VSG并网性能分析
3.1 稳态性能分析
3.1.1Droop模式稳态性能
Droop模式下,VSG有功功率输入的误差传递函数为式(6);VSG频率扰动的闭环传递函数为式(7),误差传递函数为式(8)。
(6)
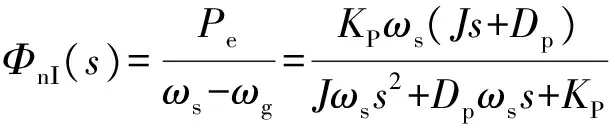
(7)
(8)
由式(1)可知,GrⅠ(s)为典型Ⅰ型系统,因而可以实现阶跃输入信号的无差跟踪,但不能实现斜坡输入信号的无差跟踪。斜率为Rp的斜坡输入信号Rp/s2作用时,输出有功功率的稳态误差为:
(9)
Droop模式下,阶跃扰动信号Δω/s和斜率为Rω的斜坡扰动信号Rω/s2作用时,稳态误差为:
(10)
3.1.2PQ模式的稳态性能及其对比分析
PQ模式下,VSG有功功率输入的开环传递函数为式(11),闭环传递函数为式(12);VSG频率扰动的闭环传递函数为式(13),误差传递函数为式(14)。
(11)

(12)

(13)
(14)
由式(11)可知,ΦrΠ(s)为典型Ⅱ型系统,因而可以实现阶跃和斜坡输入信号的无差跟踪。PQ模式下,阶跃扰动信号Δω/s和斜坡扰动信号Rω/s2作用时,输出有功功率的稳态误差为:
(15)
表1为2种模式下VSG稳态有功功率误差对比结果,可知PQ模式的稳态性能明显优于Droop模式。

表1 有功功率稳态误差对比Table 1 Comparison of steady-state active power error
3.2 动态性能分析
ΦrΠ(s)是具有闭环零点-Dp/Jv的二阶系统,零点的出现使系统响应速度加快,但超调量增大,因而PQ模式的惯性和阻尼性能均弱于Droop模式。以下对PQ模式的动态性能进行具体分析。
3.2.1功率环输入响应分析
Droop模式下,闭环系统的自然振荡角频率ωnI和阻尼比ξI分别为:
(16)
PQ模式下,闭环系统的自然振荡角频率ωnΠ和阻尼比ξΠ分别为:
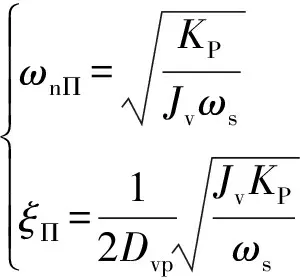
(17)
对比式(16)和式(17),可知随着Z的增大,ξΠ与ξΙ的变化规律相反。

选取Dvp=Dp,通过调节J和Jv来改变阻尼比,附录A图A3为不同阻尼比时2种模式的动态响应曲线。由图A3可知,PQ模式下Jv越大超调量越小,而响应越慢;相比于Droop模式,PQ模式的响应速度较快,但超调量和调节时间都大幅增加。因而PQ模式的动态性能弱于Droop模式。附录A图A4(a)进一步对比了不同阻尼比时2种模式的单位阶跃响应峰值。由图A4(a)可知,随着阻尼比的增大,2种模式的峰值均减小,PQ模式的峰值大于Droop模式,在过阻尼时Droop模式的峰值为1,即过阻尼时无超调量。
3.2.2功率环扰动响应分析
由式(13)可知,ΦnΠ(s)与二阶带通滤波器传递函数的结构相同,ΦnΠ(s)的通带中心频率即为ωnΠ,通带中心频率处的放大倍数为Dpωs,品质因数Q=0.5/ξΠ。因此,放大倍数与Z和Jv无关,品质因数与ξΠ呈反比关系。
在PQ模式下,通过控制参数的设计可以调整VSG对系统频率扰动的响应频段(即调整通带中心频率和品质因数),进而可以调节频率扰动下VSG为系统提供的惯性功率和能量大小;与此同时,能够保持对高频扰动的抑制和稳态输出有功功率的精确控制。
附录A图A5为不同J和Jv时的单位阶跃扰动响应曲线,由此可知:2种模式均具有惯性特性;PQ模式的调节时间较长,体现了其能够为系统提供一定的惯性功率和能量;PQ模式下,随着阻尼比的增大,超调量和调节时间都增大。附录A图A4(b)给出了不同阻尼比时2种模式的单位阶跃响应峰值。由图A4(b)可知,随着阻尼比的增大,Droop模式的峰值减小,PQ模式的峰值增大,但PQ模式的最大峰值仍小于Droop模式的最小峰值;在过阻尼时Droop模式的峰值最小,等于稳态误差值Dpωs。因而,在Dvp=Dp的条件下,PQ模式的最大峰值小于Droop模式的稳态误差值。
图5为不同J和Jv时的频率扰动闭环传递函数波特图,可知:2种模式具有相同的高频扰动抑制能力,2种模式均具有低频扰动响应能力,但PQ模式还具有超低频扰动抑制能力,即PQ模式在稳态时具有零误差的特点。图5中,随着Jv的增大,PQ模式的通带中心频率降低,通带宽度增大,但中心频率处的放大倍数不变。因此,通过参数的设计可以调整PQ模式对频率扰动的响应频段,进而可以调节PQ模式为系统提供的惯性功率和能量大小。
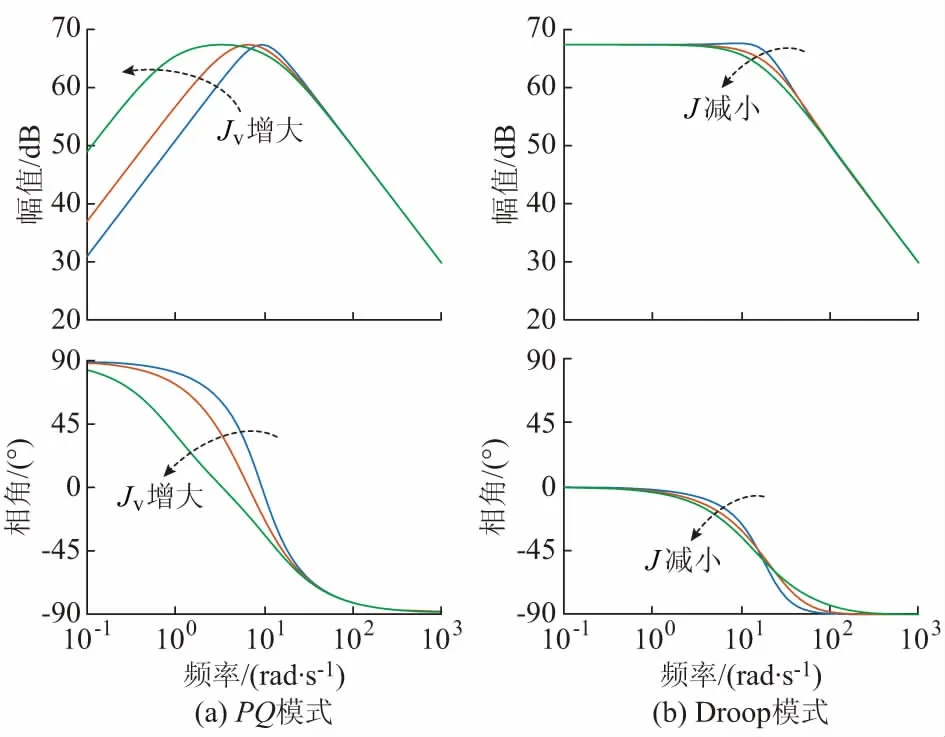
图5 不同J和Jv时的频率扰动闭环传递函数波特图Fig.5 Bode diagrams of closed-loop transfer function of frequency disturbance in the cases of different J and Jv
4 仿真和实验验证
搭建容量为10 kVA的VSG仿真模型和实验平台,对本文VSG的PQ控制模式及模式切换方法进行验证。仿真参数与第3.2节动态性能分析的参数一致,见附录B表B1。仿真和实验拓扑在图1的基础上增加了变比为150 kV/380 V的隔离变压器。仿真中未对由eabc与irefabc计算的瞬时功率进行滤波,VSG的电磁功率即为瞬时功率。附录B图B1和图B2为仿真结果。
实验中选取了过阻尼时的参数(J=0.06 kg·m2,Jv=2.4 kg·m2),其余参数见附录B表B1。实验中采用二阶带通滤波器(阻尼比为0.32)对采集到的输出端电压uabc进行滤波,之后反馈到VSG的电磁方程中,采用移动平均滤波器对瞬时有功功率50 Hz以上的谐波进行滤波,得到电磁功率Pe。图6和图7以及附录C图C1至图C6为实验结果,图中ig和iload分别为电网电流和负载电流;ug和u分别为电网电压和VSG输出电压。
4.1 VSG并网运行
仿真情形1:VSG并网运行,Pref由3.3 kW阶跃至6.3 kW。附录B图B1(a)为不同阻尼比条件下2种模式的电磁功率Pe的输入响应波形,图B1(a)中还给出了由2种模式的功率环模型得到的有功功率阶跃输入响应测试曲线,Droop模式的功率环模型见图2。对比可知:各阻尼比条件下的仿真结果与阶跃输入响应曲线能够基本重合,由仿真结果显示的2种控制模式的有功输入动静态性能与第3节的理论分析一致。
仿真情形2:VSG并网运行,电网频率骤降0.2 Hz。附录B图B1(b)为不同阻尼比条件下2种模式的电磁功率Pe的扰动响应波形,图B1(b)中还给出了频率阶跃扰动响应测试曲线。对比可知:各阻尼比条件下的仿真结果与阶跃扰动响应曲线能够基本重合,由仿真结果显示的2种控制模式的频率扰动性能与第3节的理论分析一致。
实验情形1:VSG并网运行,Pref由3.3 kW阶跃至6.3 kW。在2种模式下,VSG有功功率阶跃输入的电压电流波形和输出功率P如附录C图C1(a)和图6(a)所示,可知Droop模式的调节时间较短,为0.25 s;PQ模式的调节时间较长,为0.78 s,并且超调量大于Droop模式。稳态时,Droop模式和PQ模式的误差分别为-0.42 kW和-0.36 kW。
实验情形2:通过电网模拟器设置频率波动。电网频率骤降0.2 Hz时的电压电流波形和输出功率P如附录C图C1(b)和图6(b)所示,可知在频率突变时PQ模式下VSG可以提供0.96 s的惯性功率支撑,惯量功率最大值(功率峰值)为2.51 kW,而在Droop模式下VSG参与一次调频输出的稳态有功功率调节量为2.86 kW。显然,PQ模式的惯量功率小于Droop模式的一次调频量。
由于VSG输出电阻R和隔离变压器上的功率损耗,VSG的电磁功率Pe与输出功率P不相等。为便于比较实验和仿真结果,附录B图B2给出了J=0.06 kg·m2和Jv=2.4 kg·m2时VSG并网输出功率和扰动响应的仿真结果。在仿真和实验结果中,Droop控制模式和PQ控制模式的稳态特性保持一致,而动态特性则出现较小差别。表2至表4通过稳态误差、超调量和调节时间3个指标对理论值、仿真结果和实验结果进行比较,其中理论值由功率环线性化模型的阶跃响应得到;仿真值由输出有功功率P计算得到;调节时间特指响应到达2%误差范围所需的时间,PQ模式在扰动作用下的超调量等于功率峰值与0.4πDpωs的比值。
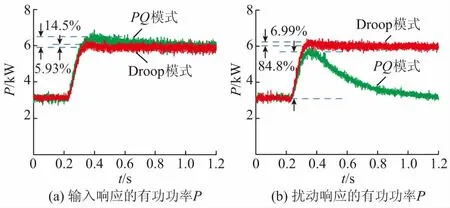
图6 并网VSG输入和扰动响应的实验结果Fig.6 Experimental results of input and disturbance responses of grid-connected VSG
由表2至表4可知,仿真值与实验值的稳态误差的差别较小,理论值、仿真值与实验值的调节时间差别也较小,而超调量具有较大差别。对于Droop模式,由于J=0.06 kg·m2时阻尼比大于1,因此理论值和仿真值的超调量均为0,但实验中应用了滤波器使得系统的动态响应性能变差,出现了5.93%(阶跃输入)和6.99%(阶跃扰动)的超调量。对于PQ模式,由于滤波器的影响使实验值的超调量大于理论值和仿真值。
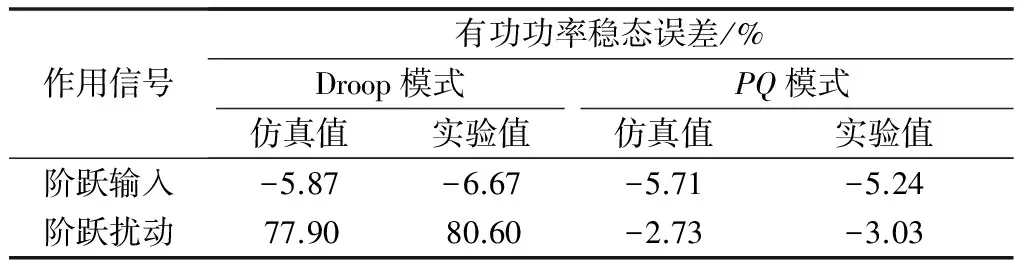
表2 有功功率稳态误差对比Table 2 Comparisons of steady-state active power error
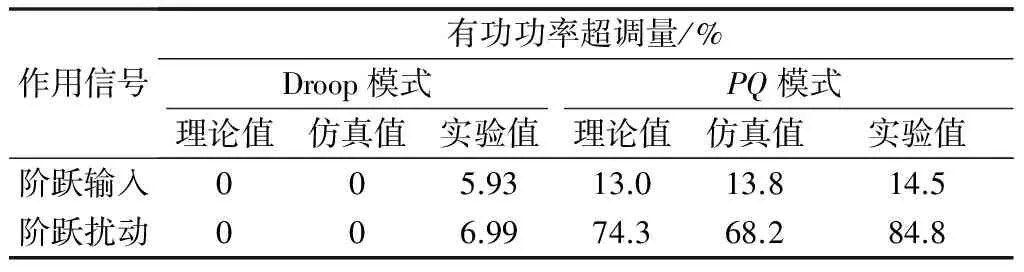
表3 有功功率超调量对比Table 3 Comparison of active power overshoot
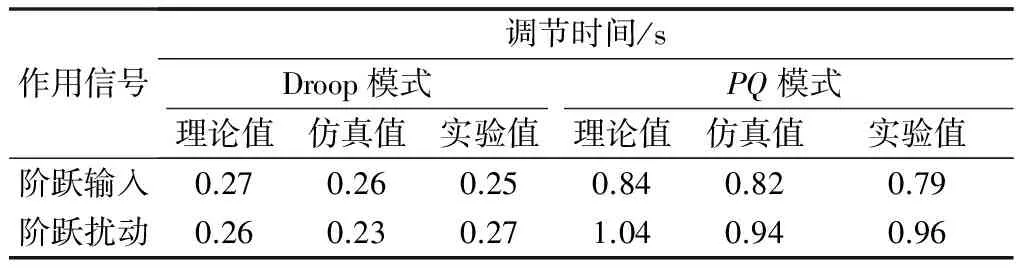
表4 有功功率调节时间对比Table 4 Comparison of active power settling time
4.2 VSG模式平滑切换
实验情形1:电网频率为49.8 Hz,并网运行VSG先由Droop模式切换到PQ模式,然后再切回Droop模式。图7为双控制模式切换的有功功率波形,附录C图C2为双控制模式切换的电压电流波形,可知:2种控制模式可以平滑切换,Droop模式向PQ模式切换的过程中无超调量,但调节时间较长(1.14 s);PQ模式向Droop模式切换的过程中有8.03%的超调量,调节时间较短(0.37 s);稳态时,PQ模式输出的有功功率为3.15 kW;而Droop模式的VSG参与了一次调频,稳态时输出有功功率为6.0 kW。
VSG控制模式切换过程分析如下。
1)Droop模式稳态时,图3中惯性环节的输入ΔT与输出Δω1满足Δω1=ΔT/Dp;切换为PQ模式的瞬间PI调节器环节的输入ΔT与输出Δω2满足Δω2=ΔT/Dvp。若Dvp=Dp,则切换前后ω未跳变,切换为PQ模式后ΔT作用于PI调节器环节的调节过程与PQ模式的有功阶跃响应相近,因而选取Dvp=Dp有利于实现控制模式的平滑切换。不同的是,Droop模式和PQ模式切换过程中未出现超调量且调节时间较长,这是由于PI调节器环节中比例环节的作用使得PQ模式在有功功率阶跃瞬间即出现了ω跳变,进而有功功率阶跃响应的动态过程快于Droop模式和PQ模式切换过程。
2)PQ模式稳态时,ΔT=0,ω=ωg,Δω2=ωg-ωs;切换为Droop模式的瞬间ΔT=0,Δω1=0,ω=ωs≠ωg。切换前后ω发生跳变,故切换为Droop模式后由ω跳变引起的调节过程与Droop模式的频率阶跃扰动响应相近。
因此,为实现VSG控制模式的平滑切换,应分析和提升2种控制模式的阶跃响应性能。

图7 并网VSG双控制模式平滑切换的实验结果Fig.7 Experimental results of smooth switchover between two control modes of grid-connected VSC
实验情形2:电网频率为50 Hz,Pref=3.3 kW,离网运行VSG接入2 kW本地负载,(在预同步使能后)VSG先进行预同步控制然后闭合并网开关。预同步单元采用PI调节器,并对PI调节器的输出进行了限幅,限值为±1.27 rad/s。预同步是否完成的判断:ab相间线电压差值Δuab=ugab-uab,当检测到4个工频周期(80 ms,对应800个采样点)的Δuab均小于设定值50 V时,认为预同步已完成。附录C图C3为VSG快速预同步并网的实验结果,附录C图C4是与图C3对应的VSG预同步并网过程中的电压差、虚拟功率和输出功率,可知:预同步在1.6 s内完成,预同步开始时的相角差为158.0°,预同步完成后再经过0.46 s的合闸判断时间并网开关闭合,最后实现了VSG无冲击电流并网。
实验情形3:电网频率为50 Hz,Pref=3.3 kW,并网运行VSG接入5 kW本地负载,在并网开关突然断开后VSG离网运行。并网开关状态检测方法:通过虚拟功率Pv的大小来检测并网开关的开合状态,当Pv>5 kW时认为并网开关已分闸。附录C图C5为VSG并离网切换的实验结果,其中,图C5(a)为并网Droop模式被动离网时的有功功率波形,图C5(b)为并网PQ模式被动离网时的虚拟功率和有功功率波形。附录C图C6是与图C5对应的VSG并离网切换的电压、电流波形。由实验结果可知,Droop模式的被动离网切换具有较好的动态性能;PQ模式被动离网切换时并网开关分闸状态的检测时间约为10 ms,在此时间段内,离网PQ模式的VSG通过惯性特性来维持系统的稳定,使得被动并离网过程中电压、电流只出现了5 ms的较小波动,在检测到并网开关断开后通过PQ控制模式向Droop控制模式的迅速切换,实现了VSG被动并离网平滑切换。
5 结语
本文主要针对双模式运行VSG的控制策略进行研究,提出一种VSG的并网功率控制策略。通过理论分析和仿真、实验验证,所得结论如下所示。
1)并网运行时PQ控制模式可实现无锁相环的自同步运行;PQ模式可实现电网频率扰动下恒定稳态功率控制,也即不参与电网的一次调节;PQ模式可以与Droop模式实时切换,通过PQ模式向Droop模式的实时切换可以实现VSG被动并离网工况的平滑切换。
2)与现有VSG的Droop模式相比,PQ模式的特点是:电网频率发生波动时,2种模式均可提供惯性功率支撑,但PQ模式具有更好的稳态性能;PQ模式有功功率输入的动态性能弱于Droop模式。因此,对于需要配置储能单元的VSG,考虑到储能单元电量约束,并网运行时PQ模式可以作为现有Droop模式VSG的有效补充,在电量不足时切换为PQ模式的VSG不参与一次调频,只为系统提供惯性功率支撑。
由于本文仿真和实验中VSG直流侧采用的是直流电压源,未考虑分布式能源与储能的特性,因此PQ控制模式在实际环境中的适用性还有待进一步研究。
本文得到国网辽宁省电力有限公司2018年科技项目“考虑源、荷波动特征的电网无功电压优化策略和评价指标研究”的资助,谨此致谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 吕志鹏,盛万兴,刘海涛,等.虚拟同步机技术在电力系统中的应用与挑战[J].中国电机工程学报,2017,37(2):349-359.
LÜ Zhipeng, SHENG Wanxing, LIU Haitao, et al. Application and challenge of virtual synchronous machine technology in power system[J]. Proceedings of the CSEE, 2017, 37(2): 349-359.
[2] ZHONG Qingchang, NGUYEN P L, MA Zhenyu, et al. Self-synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 617-630.
[3] WANG Shuo, HU Jiabing, YUAN Xiaoming. Virtual synchronous control for grid-connected DFIG-based wind turbines[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 932-944.
[4] ALATRASH H, MENSAH A, MARK E. Generator emulation controls for photovoltaic inverters[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 996-1011.
[5] 曾正,邵伟华,冉立,等.虚拟同步发电机的模型及储能单元优化配置[J].电力系统自动化,2015,39(13):22-31.DOI:10.7500/AEPS20140901007.
ZENG Zheng, SHAO Weihua, RAN Li, et al. Mathematical model and strategic energy storage selection of virtual synchronous generators[J]. Automation of Electric Power Systems, 2015, 39(13): 22-31. DOI: 10.7500/AEPS20140901007.
[6] 石荣亮,张兴,徐海珍,等.基于虚拟同步发电机的微网运行模式无缝切换控制策略[J].电力系统自动化,2016,40(10):16-23.DOI:10.7500/AEPS20150615012.
SHI Rongliang, ZHANG Xing, XU Haizhen, et al. Seamless switching control strategy for microgrid operation modes based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2016, 40(10): 16-23. DOI: 10.7500/AEPS20150615012.
[7] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):591-603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in mcrogrid[J]. Proceedings of the CSEE, 2014, 34(16): 591-603.
[8] 颜湘武,刘正男,张波,等.具有同步发电机特性的并联逆变器小信号稳定性分析[J].电网技术,2016,40(3):910-917.
YAN Xiangwu, LIU Zhengnan, ZHANG Bo, et al. Small-signal stability analysis of parallel inverters with synchronous generator characteristics[J]. Power System Technology, 2016, 40(3): 910-917.
[9] 孙孝峰,郝彦丛,王宝诚,等.微电网分布式储能单元荷电状态平衡和电压恢复[J].中国电机工程学报,2016,36(15):4047-4054.
SUN Xiaofeng, HAO Yancong, WANG Baocheng, et al. State-of-charge balancing of distributed energy storage units and voltage restoration in microgrid[J]. Proceedings of the CSEE, 2016, 36(15): 4047-4054.
[10] 徐海珍,张兴,刘芳,等.基于微分补偿环节虚拟惯性的虚拟同步发电机控制策略[J].电力系统自动化,2017,41(3):96-102.DOI:10.7500/AEPS20160420001.
XU Haizhen, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator based on differential compensation virtual inertia[J]. Automation of Electric Power Systems, 2017, 41(3): 96-102. DOI: 10.7500/AEPS20160420001.
[11] TORRES L M A, LOPES L A C, MORN T L A, et al. Self-tuning virtual synchronous machine: a control strategy for energy storage systems to support dynamic frequency control[J].IEEE Transactions on Energy Conversion, 2014, 29(4): 833-840.
[12] 张波,颜湘武,黄毅斌,等.虚拟同步机多机并联稳定控制及其惯量匹配方法[J].电工技术学报,2017,32(10):42-52.
ZHANG Bo, YAN Xiangwu, HUANG Yibin, et al. Stability control and inertia matching method of multi-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 42-52.
[13] 张昌华,钟庆昌,曹永兴,等.一种具有同步发电机特性的逆变控制器:CN103066876A[P].[2013-01-17].
[14] SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.
[15] TENG Wu, LIU Jinjun, ZENG Liu, et al. Load power estimation based secondary control for microgrids[C]// Proceedings of Ninth International Conference on Power Electronics-ECCE, June 1-5, 2015, Seoul, South Korea: 722-727.
[16] 魏亚龙,张辉,孙凯,等.基于虚拟功率的虚拟同步发电机预同步方法[J].电力系统自动化,2016,40(12):124-129.DOI:10.7500/AEPS20150727006.
WEI Yalong, ZHANG Hui, SUN Kai, et al. Pre-synchronization method of virtual synchronous generator using virtual power[J]. Automation of Electric Power Systems, 2016, 40(12): 124-129. DOI: 10.7500/AEPS20150727006.
[17] ZHONG Q C, NGUYEN P L. Sinusoid-locked loops based on the principles of synchronous machines[C]// Proceedings of the 24th Chinese Control and Decision Conference, May 23-25, 2012, Taiyuan, China: 1518-1523.
[18] 蒋连钿,张明,庄革,等.三相PWM整流器中基于虚拟无功的锁相环[J].电工技术学报,2013,28(8):212-217.
JIANG Liandian, ZHANG Ming, ZHUANG Ge, et al. A phase-locked loop method for three-phase PWM rectifier based on virtual reactive power[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 212-217.
[19] 赵耀,王建,杨晓梅,等.有零点二阶系统的动态性能分析[J].电气电子教学学报,2013,35(3):11-14.
ZHAO Yao, WANG Jian, YANG Xiaomei, et al. Dynamic performance analysis of second-order systems with a Zero[J]. Journal of Electrical & Electronic Engineering Education, 2013, 35(3): 11-14.
[20] 滕青芳,范多旺,董海鹰,等.自动控制原理[M].北京:机械工业出版社,2015:66-80.
颜湘武(1965—),男,教授,博士生导师,主要研究方向:新能源电力系统分析与控制、现代电力变换、新型储能与节能技术。E-mail: xiangwuy@ncepu.edu.cn
贾焦心(1991—),男,通信作者,博士研究生,主要研究方向:微电网运行及接口变换器控制。E-mail: jiajx33@163.com
王德胜(1994—),男,硕士研究生,主要研究方向:虚拟同步发电机及其在微电网的应用。E-mail: deshengw@foxmail.com

