一道课本题的多解、多变与多用

马爱平 陈德前

(1.江苏省兴化市戴泽初级中学 225721; 2.江苏省兴化市教育局教研室 225700)

义务教育教科书人教版八年级下册第62页第13题是：

题目如图1，E，F，M，N分别是正方形ABCD四条边上的点，且AE=BF=CM=DN.试判断四边形EFMN是什么图形，并证明你的结论.

一、在一题多解中复习知识

经过测量、观察可知四边形EFMN是正方形，通过对这个结论多种证明方法的研究可巩固平行四边形、菱形、矩形、正方形、全等三角形及勾股定理等众多知识.

思路1 先证明四边形EFMN是平行四边形，再证明它有一个角是直角和一组邻边相等.

思路2 先证明四边形EFMN是矩形(证三个角是直角)，再证明有一组邻边相等

思路3 先证明四边形EFMN是菱形(证四边相等)，再证明有一个角是直角.而证明四边相等又有两种方法：一是通过证明△NAE≌△EBF≌△FCM≌△MDN得到，二是利用勾股定理证明得到.

下面只给出思路3的证明，其他思路的解题过程请同学们作为练习，自己给出.

方法1 ∵四边形ABCD是正方形，∴AB=BC=AD，∠A=∠B=90°.∵AE=BF=DN，∴BE=AN，∴△NAE≌△EBF，∴EN=EF，∠AEN=∠BFE.同理可证EN=EF=FM=MN，∴四边形EFMN是菱形.∵∠B=90°∴∠BEF+∠BFE=90°，∴∠AEN+∠BEF=90°，∴∠NEF=180°-90°=90°，∴四边形EFMN是正方形.

方法2 ∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠A=∠B=∠C=∠D=90°.∵AE=BF=CM=DN，∴BE=CF=DM=AN，∴由勾股定理得EN=EF=FN=MN，∴四边形EFMN是菱形.下同方法1，略.

通过上述一题多解，我们不仅复习了平行四边形、菱形、矩形、正方形的判定方法，而且对四边形、平行四边形、矩形、菱形、正方形之间的知识结构会变得十分清晰.

二、在一题多变中学会探索

在一题多解的基础上，研究题目的多种变式，不仅可以提高我们的应变能力，而且能使我们在变式中学会探索，学会学习.

变式1 将点E，F，M、N特殊化，变成正方形ABCD各边的中点，则有：

如图2，E，F，G，H分别是正方形ABCD各边的中点.四边形EFGH是什么四边形？为什么？(课本八年级下册第67页复习巩固第6题)

解析很明显四边形EFGH仍是正方形，证明这个结论除上述方法外，还可连AC和BD，利用三角形中位线定理，先证明四边形EFGH是平行四边形，再证明它有一个角是直角和一组邻边相等(请同学们自己写出证明过程).

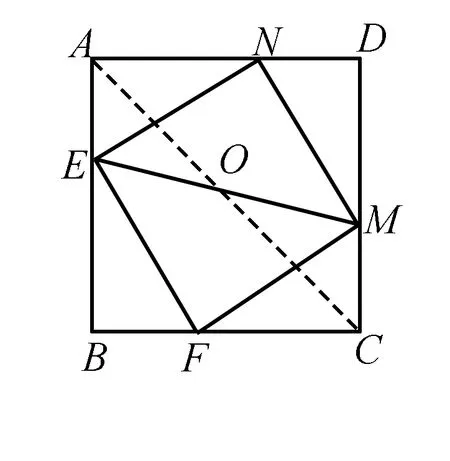
变式2 由变式1可发现，EG和FH一定经过正方形ABCD对角线的交点，那么在一般情况下这个结论是否成立呢？于是有：

如图3，E，F，M，N分别是正方形ABCD四条边上的点，且AE=BF=CM=DN.试判断直线EM是否经过一个定点，并说明理由.

分析连接AC、BD和EM发现它们交于一点，将图4绕正方形ABCD对角线的交点旋转也可得到这个结论，于是猜想直线EM经过一个定点(即正方形对角线的交点).然后证明这个结论正确即可.下面给出三种证明方法：

方法1 如图3，连接AC，设AC、EM相交于点O.∵四边形ABCD为正方形，∴AB∥CD，∴∠AEO=∠CMO，∠EAO=∠MCO.又∵AE=CM，∴△AEO≌△CMO，∴AO=CO.∵AC一定，∴O为定点，即EM一定经过正方形对角线的中点.

方法2 如图3，AC,设AC、EM相交于点O.∵四边形ABCD为正方形，∴AB∥CD，即AE∥CM.又∵AE=CM，∴四边形AECM是平行四边形，∴AO=CO.而AC一定，∴O为定点，即EM一定经过正方形对角线的中点.

方法3 如图3连接AC、BD，设AC、BD相交于点O.连接EO、MO.∵四边形ABCD为正方形，∴AB∥CD，AO=CO，∴∠EAO=∠MCO.又∵AE=CM，∴△AEO≌△CMO，∴∠AOE=∠COM.∵∠AOM+∠COM=180°，∴∠AOM+∠AOE=180°，即E、O、M三点共线，∴EM一定经过正方形对角线的中点.

变式3 在变式2的探索中，我们发现随着点E，F，M，N的变化，正方形EFMN的面积也在变化，很明显它有最大值，即正方形ABCD的面积，那么有没有最小值呢？于是又有：

如图4，正方形ABCD的边长为8cm，点E、F、G、H分别是AB、BC、CD、DA上的动点，且AE=BF=CG=DH.试问四边形EFGH面积是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由.

分析在图形的旋转中，我们发现，当E、F、G、H分别为AB、BC、CD、DA的中点时，S正方形EFGH最小，因此只要通过推理得到这个结论即可.

通过一题多变，我们得到了三个有价值的问题，其实我们还可以通过变式得到许多问题，同学们可以自己试一试.

三、在一图多用中提升能力

由图1，我们可以得到这样一个基本模型：

如图5，点E在线段BC上，∠ABE=∠AEF=∠ECF=90°，BE=CF，则△ABE≌△ECF.由于这个图形象“凹槽”，所以我们把它称为“凹槽全等型”，Rt△AEF称之为“凹槽直角三角形”.应用这个基本模型及其性质可以简捷地解决许多问题.

1.模型具备直接用

例1 如图6，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，则EF的长为 .

解析在正方形ABCD中，∠BAD=90°,AB=AD.∵BF⊥a于点F，DE⊥a于点E,∴∠BFA=∠DEA=∠BAD=90°.由上述基本模型和性质可得△ABF≌△DAE，∴AF=DE,BF=AE，∴EF=AF+AE=DE+BF=8+5=13.

2.模型残缺补全用

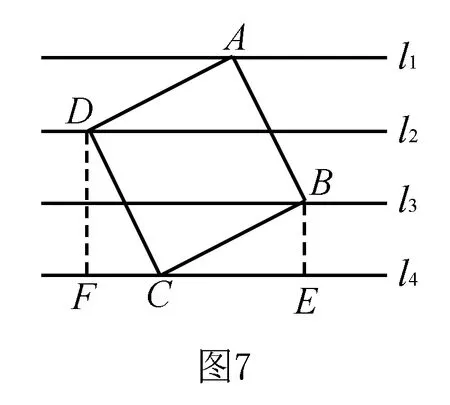
例2 如图7，平面内4条直线l1、l2、l3、l4是一组平行线，相邻2条平行线的距离都是1个单位长度，正方形ABCD的4个顶点A、B、C、D分别在这些平行线上，该正方形的面积是____平方单位.

解析如图7，分别过点B、D作直线l4的垂线，垂足分别为E、F.由上述基本模型和性质可得△DFC≌△CEB,∴FC=EB=1.又∵DF=2,∴S正方形ABCD=DC2=DF2+FC2=5.

3.多个模型反复用

例3 如图8①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.

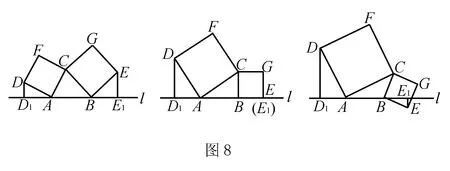
(1)如图8②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB；

(2)在图8①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由；

(3)如图8③,当点E在直线l的下方时,请写出三条线段DD1、EE1、AB之间的数量关系，并说明你的理由.

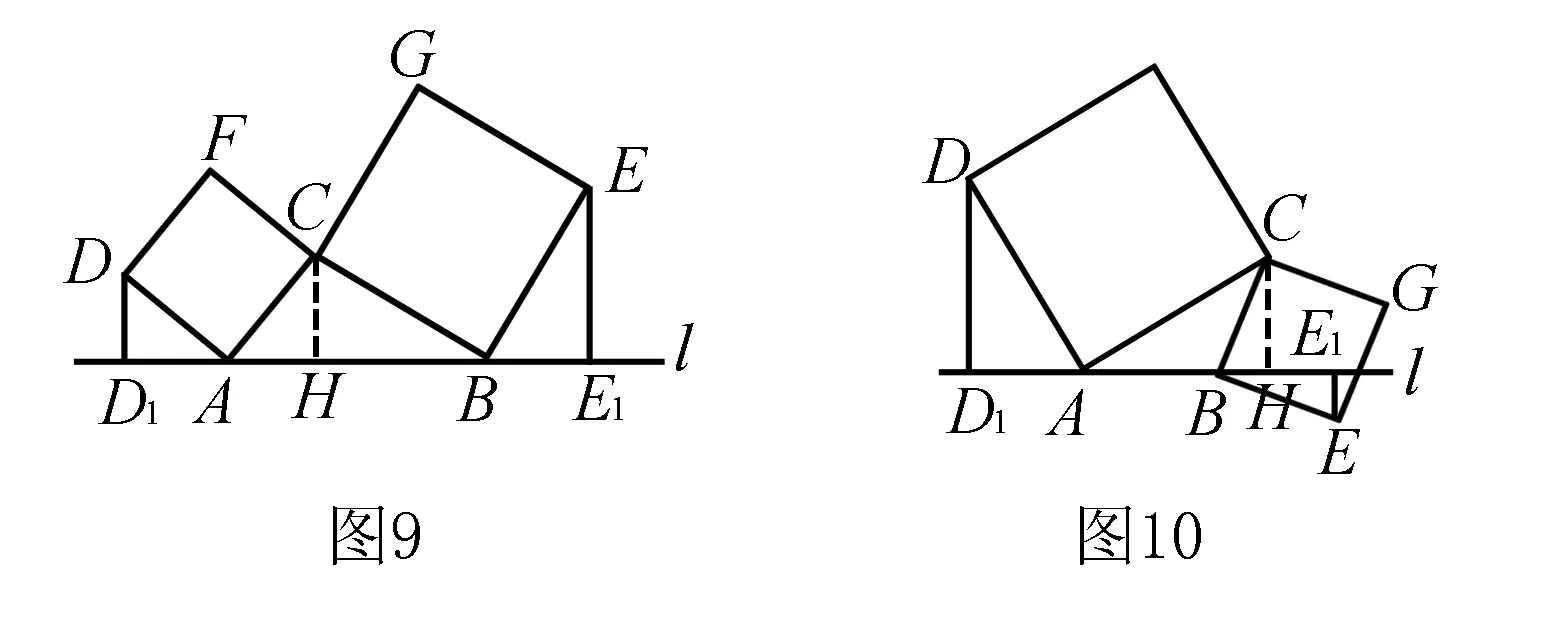
解析(1)由上述基本模型及其性质可得△ADD1≌△CAB，∴DD1=AB.

(2)DD1+EE1=AB，理由如下：如图9，过点C作CH⊥l，垂足为H，由上述基本模型及其性质可知△ADD1≌△CAH，△BEE1≌△CBH，∴DD1=AH,EE1=BH,∴DD1+EE1=AH+BH=AB.

(3)DD1-EE1=AB，理由如下：如图10，过点C作CH⊥l，垂足为H，由上述基本模型及其性质可知△ADD1≌△CAH，∴DD1=AH.再通过证明△BEE1≌△CBH，可知EE1=BH，∴DD1-EE1=AH-BH=AB.

以上我们通过模型的发现与构造，顺利找到了解决问题的途径，由此足见模型的巨大作用，我们在复习中要善于提炼基本模型，并灵活运用它来分析问题和解决问题.

参考文献：

[1]陈德前，王朝珍.利用典型考题 提高复习效率[J].中国数学教育(初中)，2017(4)：12-16.

[2]霍彩霞.如何进行审题[J].初中生学习指导(七年级)，2016(7-8)：98-101.