钢箱梁悬索桥模态阻尼比分析

杨舒蔚, 葛容华

(西南交通大学土木工程学院，四川成都 610031)

阻尼问题是动力学计算中必须考虑的一个重要问题。研究结构的实际阻尼特性既可以揭示结构的动力特性，以确定计算模型中合理的阻尼特性，同时也是评价现有阻尼计算模型适用性以及确定计算参数的重要依据。悬索桥的实际阻尼特性一般是通过模态阻尼比来表征的。从阻尼比与自振频率的相对关系的角度研究阻尼无论从理论表述或者是实际运用均是非常方便的。

研究阻尼特征的基本方法是采用实际测量的方式，目前中外都累积了大量的数据。在此基础之上，Davenport[1]在1989年通过经验数据拟合提出了一个经验公式。郭震山[2]对其在虎门大桥(钢箱梁悬索桥)的实测数据进行了拟合，也取得了较好的效果，但该方法并未在后期建设的诸多大跨径钢箱梁悬索桥的模态测量数据中进行验证，因而不能确定是否适用于其它钢箱梁悬索桥。Brownjohn[3]分析了悬索桥的阻尼来源并探究了实测数据误差的来源，从理论上指出风速、非线性效应等均会在一定程度上影响结果。同济大学防灾重点实验室在对泰州长江大桥进行模型试验[4]后指出是否采用阻尼器对结构阻尼比的测试结果也有重大的影响。Kawashima[5]基于模型试验的方法，为斜拉桥提出了一个基于能量损失率的阻尼比估计理论，郭震山[6]将其推广至悬索桥上使用，但仅在一座悬索桥上进行过计算。进入21世纪之后，悬索桥的模态阻尼比估算方法基本上采用环境激励法，但在数据处理上产生了多种方法，由此导致部分结果可能会产生较大的差异。总之，目前悬索桥的实测数据的精度与完整程度受客观环境的影响均存在一定的问题。因此精确地拟合悬索桥阻尼比是意义不大的，应将重点着重于在设计工程范围内可接受的悬索桥模态以及阻尼比的变化趋势上。

1 悬索桥阻尼数据拟合方法

悬索桥阻尼实测数据很多，对这些数据进行拟合分析是非常困难的。一方面，悬索桥阻尼机制非常复杂，很难提出合适的理论公式或者半经验公式进行拟合。另一方面，悬索桥阻尼比测量数据受其测量方式的影响，其离散程度较大。该部分对于数据的拟合应使得拟合公式在工程意义上可以为悬索桥阻尼的判断分析提供依据。

1.1 拟合公式的选定

Davenport[1]提出悬索桥结构的阻尼比与振型频率关系可以用下面的经验公式表示：

lg(ξ)=blg(f)+a

(1)

在上面的经验公式下，Davenport在对美国的一些悬索桥阻尼比实测数据进行拟合后，认为参数b应当是一个在-1附近的数字，即随着频率的增大，阻尼比会减小，表示在对数坐标下阻尼比的衰减率。然而Davenport的主要研究对象是美式的桁架式悬索桥，虽然郭震山[2]对虎门大桥的研究得到了类似的结论，但样本太小，无法说明钢箱梁悬索桥这一类结构的特性。事实上，由于悬索桥这一类结构在实际中需要考虑大量的模态，因此中高阶振型的模态并非是完全可以忽略的。但参数b小于0，因而式(1)是一个递减函数，这意味着阻尼会无限制的递减下去直至无穷小，这显然是不够合理的。事实上，从本文收集到的阻尼数据(图1(g)～图1(j))来看，达到一定的频率后，结构的阻尼比不会继续变小，而会在一定范围内波动。为了可以较好地表征出悬索桥模态的这一特性，我们可以简单地认为大于某一频率fh后结构阻尼比为一常数，即将式(1)扩展为：

(2)

1.2 实测数据处理及离散程度分析

直接用式(2)的分段函数进行拟合是有难度的，从悬索桥阻尼比数据来看，该类悬索桥的模态的振动频率数据在达到0.5 Hz左右后阻尼比已经基本达到了较低的水平，因此对于该类悬索桥，我们可以假设fh=0.5 Hz,然后分别进行拟合。

设ξ*(f) 为结构自振频率为f的模态的精确阻尼比，ξ(f)为用上式拟合后的阻尼比，e为拟合值的最大误差。则有：

(3)

若设ξu(f)、ξl(f)为结构的阻尼比上下限，即:

ξu(f)≤ξ*(f)≤ξl(f)

(4)

比较式(3)与式(4)可得：

ξu(f)=(1+e)ξ(f)

(5)

ξl(f)=(1-e)ξ(f)

(6)

在对数坐标下拟合线ξ(f)是一条折线，由式(5)与式(6)可以看出，上限ξu(f)与下限ξl(f)是两条与拟合线平行的折线，其间形成了一个带状区域是实际阻尼比可能落入的区域。考虑到测量带来的偶然误差等因素，在实际处理中，个别数据可能极大地离散于拟合的曲线，所以在确定拟合阻尼比的上下限时，使绝大部分数据位于这个上下限内便可。这里采用的做法是使总体数据的90 %位于上下限区域内。

2 悬索桥阻尼数据拟合结果

本文收集了国内外各种形式的十座钢箱梁悬索桥的阻尼比实测数据[7-15]，其中有较大的比重是2000年前后新建的大跨度悬索桥。对于各桥梁的阻尼比实测数据进行拟合后，将拟合参数结果、桥梁的主要特性列于表1中，而拟合线及原始横向、竖向振型的阻尼比数据见图1。同时图1中还绘制了式(5)与式(6)所表示的拟合上下限。

在进行数据分析时还进行了如下的处理：

(1)环境随机振动法测阻尼时其结果受风速影响很大，对于有多组不同风速下的测试数据，本文取阻尼比较小的那一组，这样分析下的结果是偏于安全的。

(2)在有多种测试方法，并且有多组数据的情况下，采取整体阻尼比较小的那一组，差别不大时，取测量时间较晚、测试手段较新的那一组。

(3)悬索桥阻尼数据都表现出一定的离散性，因此图中还绘制出拟合结果上限，拟合结果下限。上下限的确定是使得90 %以上的数据满足式(4)。各桥产生上下限的拟合离散参数e代表了结构的数据的离散程度。

(4)部分桥梁的测试资料上对于某些模态注明其结果不可靠，则在拟合时忽略掉这些模态。

表1 本文所考察钢箱梁悬索桥阻尼特性拟合

3 悬索桥模态阻尼特性

若要依据式(2)完全确定悬索桥的阻尼比拟合模型，则需要确定拟合参数a、拟合参数b两个参数，或者通过两个频率(结构基频与分段函数交界处0.5Hz)处的阻尼比反算。图2给出了不同桥梁拟合参数b的分布，表2与图3则给出了各桥梁关键频率处拟合阻尼比。

分析图表可以看出钢箱梁悬索桥的模态阻尼比具有以下几个明显的特性：

(1) 对于拟合参数b，据其基频的大小，基本可以分为两大类。一类是柔度很大，基频小于0.7 Hz的大跨度悬索桥，他们的跨度在1 300 m以上，其衰减比在-0.2～-1之间呈现出非常大的离散；另一类是基频大于0.7 Hz跨度在1 300 m之下的悬索桥，其衰减比一般位于-1.0～-1.3之间，平均为-1.2。

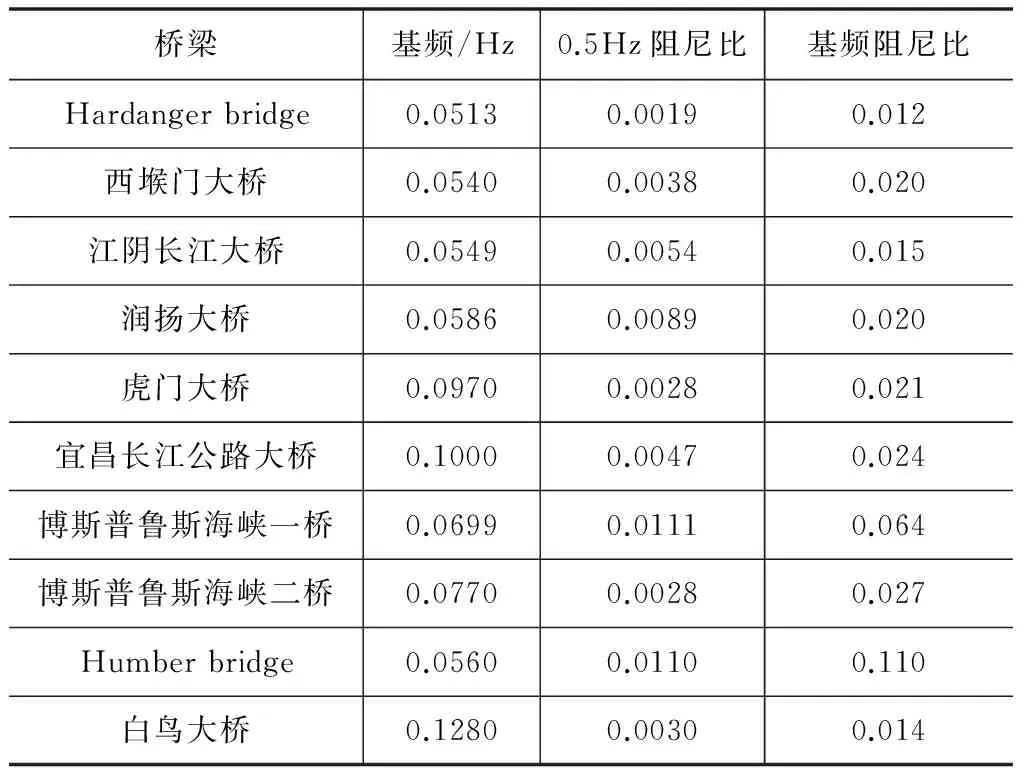
表2 悬索桥关键频率处拟合阻尼比

(a) Hardanger bridge

(b)西堠门大桥

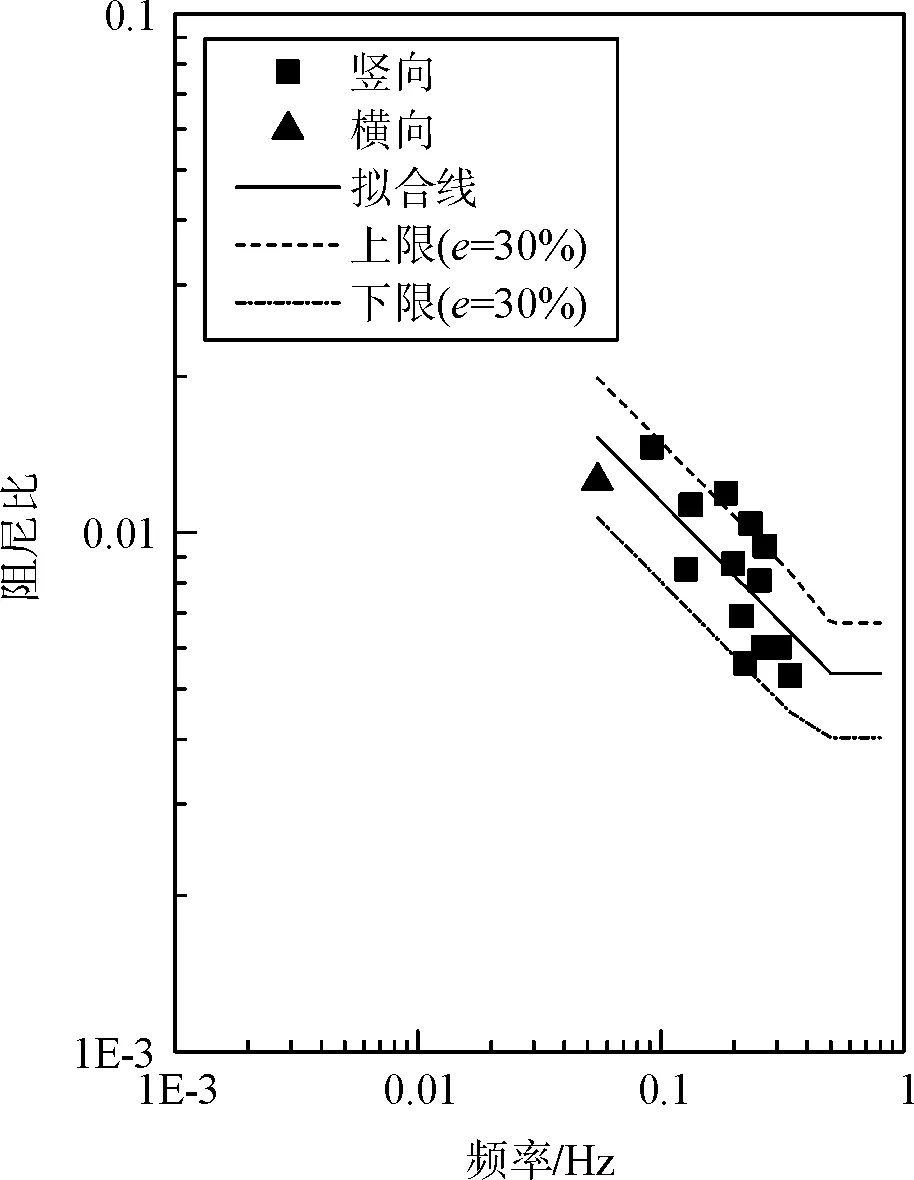
(c)江阴长江大桥

(d)润扬长江大桥

(e)虎门大桥

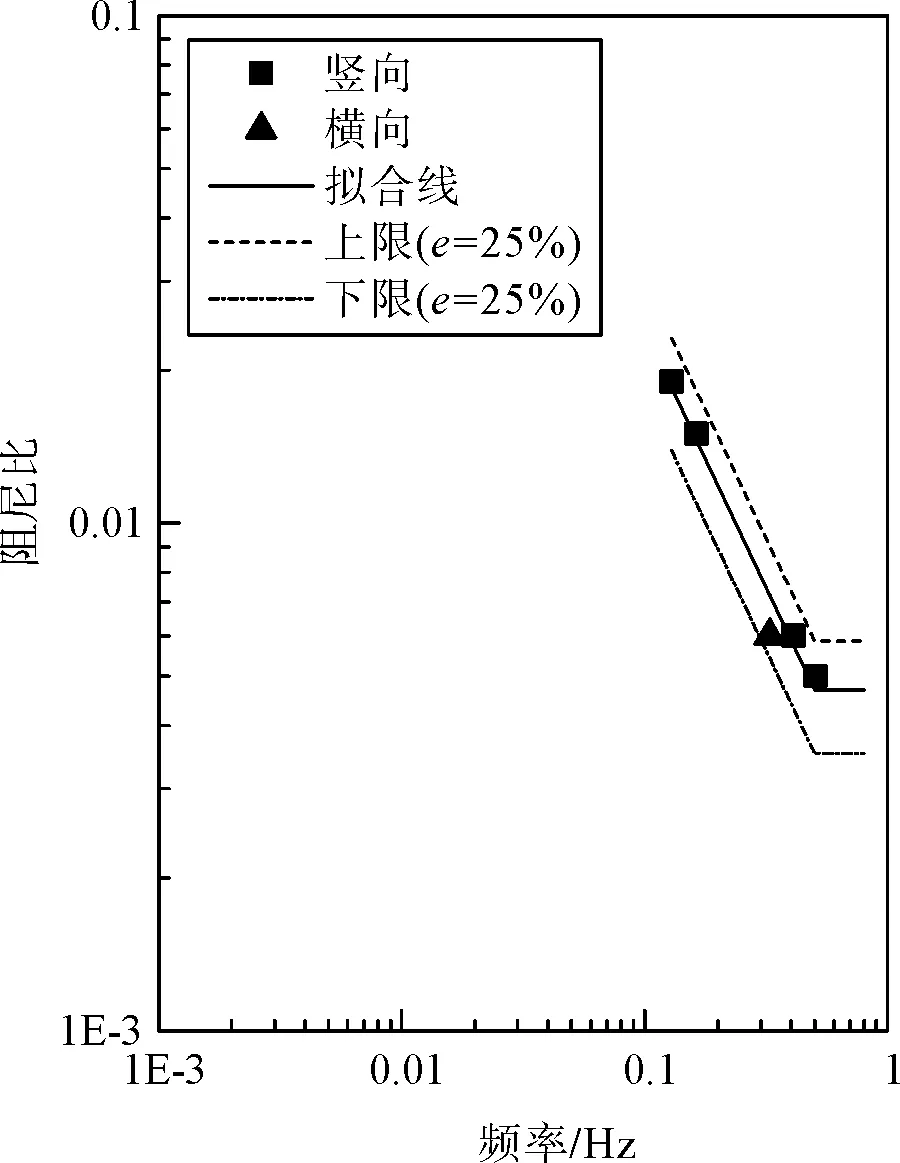
(f)宜昌长江公路大桥

(g)博斯普鲁斯海峡一桥

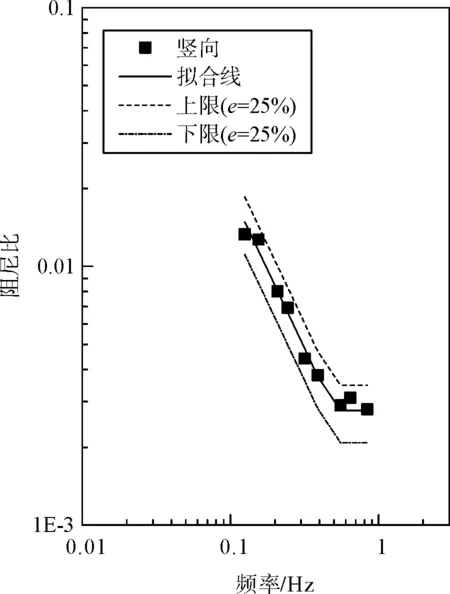
(h)博斯普鲁斯海峡二桥

(i)Humber bridge

(j)白鸟大桥

图2 拟合参数b随基频频率的关系

(a)基频处

(b)0.5Hz处图3 关键频率处拟合阻尼比随基频频率的关系

(2) 钢箱梁悬索桥的阻尼比拟合结果在各桥的基频处的阻尼比除两座斜吊索悬索桥(Humber bridge与博斯普鲁斯海峡一桥)外，均位于0.01～0.03之间，大部分位于0.02左右。斜吊索悬索桥之所以比较高，可能是因为斜吊索构成的空间桁架体系有效的增大了能量耗散，造成基频阻尼比的提高。

(3) 拟合曲线认为阻尼比在0.5 Hz之后将会为常值，从图1(g)～图1(j)的拟合结果来看，这个假定是合理的。

(4) 0.5 Hz处的阻尼比各桥大概在0.002～0.006之间。同样斜吊索悬索桥表现出了较高的结果，大概在0.01左右。值得注意的是，润扬大桥同样具有较高的阻尼比，推测这有可能是中央扣的设置限制了缆索的位移，增大了能量消耗与阻尼比。

本文的数据可以较好地用于悬索桥模态阻尼比的估计与预测，具体来说：

(1)估算基频阻尼比。对于本文研究的跨度600 m以上的悬索桥可取为0.02 Hz，可视情况略微在0.015～0.025间微调。

(2)估算0.5 Hz处的阻尼比可取为0.003，对于拥有中央扣等结构的悬索桥该值可适度放大，但取0.003是较为安全的估计。

(3)得到关键处的阻尼比后利用式(2)反算结构的阻尼比曲线，为便于计算，公式的参数可取fh=0.5 Hz。

4 结 论

本文通过改进Davenport的悬索桥模态阻尼比与频率间的经验拟合式，提出了新的经验公式，并利用该式对国内外的10座悬索桥的阻尼比实测数据进行了拟合。得到了如下结论：

(1)本文提出的两段式的拟合函数可以比较好地拟合悬索桥的阻尼特性，将高频处的阻尼比拟合为一常数，从而避免了原公式阻尼比无限减小的问题。

(2)悬索桥基频阻尼比除斜吊索体系外，绝大多数位于0.02附近，而高频处的恒定阻尼比除斜吊索体系及带有中央扣的悬索桥，基本在0.004附近。

(3)通过估计悬索桥在基频的阻尼比及高频的恒阻尼比，可以得到悬索桥阻尼的估测值以在设计中用以预测悬索桥阻尼特性。

[1] Davenport A.G.Larose G. The structural damping of long span bridges: an interpretation of observations[A]. Proc.

[2] 郭震山,陈艾荣,项海帆. 大跨缆索承重桥梁的结构阻尼特性[J]. 世界地震工程,2000(3):52-57.

[3] Brownjohn J M W. Estimation of damping in suspension bridges[J]. Structures & Buildings, 1994, 104(4):401-415.

[4] 闫聚考,彭天波,李建中.泰州长江公路大桥振动台试验——试验设计及抗震结构体系试验结果分析[J].东南大学报: 自然科学版,2014(2):357-362.

[5] Kawashima K et al. Estimation of damping ratio of cable-stayed bridges for seismic design[J]. Journal of Structural Engineering. 1993, 119(4):1015-1031.

[6] J.M.W. Brownjohn, Filipe Magalhaes, Elsa Caetano, Alvaro Cunha. Ambient vibration re-testing and operational modal analysis of the Humber Bridge[J]. Engineering Structures 2010， 32: 2003-2018.

[7] O. Øiseth, A. Rönnquist, K.A. Kvåle, R. Sigbjörnsson. Monitoring wind velocities and dynamic response of the Hardanger Bridge [J]. Conf ProcSoc Exp Mech Ser, 2015 (2): 117-125.

[8] 徐良,江见鲸,过静珺. 广州虎门悬索桥的模态分析[J]. 土木工程学报,2002(1):25-27.

[9] 王春苗. 基于环境激励测试值的润扬悬索桥动力特性分析[J]. 公路交通科技,2006(11):56-59.

[10] 郑凯锋,夏招广,佘川. 宜昌长江公路大桥悬索桥动力试验和计算研究[J]. 中国铁道科学,2002(5):103-109.

[11] Brownjohn J M W, Dumanoglu A A, Severn R T. Ambient vibration survey of the fatih sultan mehmet (second Bosporus) suspension bridge[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(10):907-924.

[12] Brownjohn J M W, Dumanoglu A A, Severn R T, et al. Ambient vibration survey of the bosporus suspension bridge[J]. Earthquake Engineering & Structural Dynamics, 1989, 18(2):263-283.

[13] 宋晖, 沈旺, 王昌将. 西堠门大桥建设关键技术[M].北京:人民交通出版社, 2015.

[14] Abe M,Fujino Y,Yanagihara M,Sato M. Monitoring of Hakucho Suspension Bridge by ambient vibration measurement[C]. Proceedings of the International Society for Optical Engineering SPIE, 2000:223-244.

[15] 张宇峰,张传刚,承宇,等. 基于GPS技术的江阴长江公路大桥动力特性分析[J].公路,2010(2):5-7.