反基础模型论解悖方法探析

赵 鹏

（河南工业大学马克思主义学院，河南郑州 450001）

“逻辑学家憎恨歧义但是喜欢悖论。”［1］3两千多年来，悖论一直以其自身的巨大魅力吸引着众多学者的研究兴趣。20世纪80年代，非良基集合论的兴起为学者们研究悖论问题提供了一个新视角。1987年，巴威斯（Jon Barwise）和艾克曼迪（John Etchemendy）在《说谎者：论真和循环》一书中把超集理论应用于情境语义学，创立了情境语义学解悖方案，用奥斯汀型阐释相对合理地解决了说谎者悖论和被称为语义学黑洞的强化的说谎者悖论。1996年，巴威斯和莫斯（Lawrence Moss）在《恶性循环：非良基现象的数学》一书中把超集理论应用于模型论，构造了解悖的数学框架——反基础模型论，其采用的方法可称之为反基础模型论解悖方法［2］100。

本文基于反基础模型论的基本理论，以说谎者悖论、强化的说谎者悖论、佐丹卡片悖论这三个包含真谓词的自指悖论为例，不仅重点阐释和具体说明了反基础模型论解悖方法的巧妙之处，同时还指出反基础模型论解悖方法揭示了悖论产生的根源，以及这一理论在消解其他自指的语义悖论（如指称悖论）方面所独具的价值。

一、反基础模型论的基本理论

巴威斯和莫斯使用了部分模型和克里尼三值逻辑的一些概念和结论。他们用Rel表示关系符号的集合，用Const表示常量的集合，用Var表示变量的集合。同时假定Rel∩Const∩Var＝∅，Var是无穷的，Rel中每一个关系符号R都有一个确定的元数，说明R是一个n元的关系符号，n为大于零的自然数。语句是通过逻辑联结词 、和∃作为初始符号构造起来的。

定义1（部分模型） 一个部分模型M是一个满足下列条件的六元组〈DM，LM，ExtM，AntiM，dM，cM〉：

（1）DM是一个非空集合，称作M的定义域；

（2）LM⊆Rel∪Const，称作 M的语言；

（3）ExtM和AntiM是定义在LM∩Rel上的两个函数，并且满足条件：对于每一个n元关系符号R∈LM，ExtM（R）和AntiM（R）是DM上两个不相交的n元关系，分别称它们为R在M中的外延和反外延；

（4）dM是从LM∩Const到DM上的一个映射；如果dM（c）＝b，则称b为常项符号 c在M中的指派；

（5）M的情境cM是从Var的一个子集到DM上的一个映射；如果cM（v）＝b，则称b为变项符号 v在M中的指派。

t在模型M中的指派记作denM（t）。如果t是一个常项，则称t在模型M中的指派为dM（t）；如果t是一个变项，则称t在模型M中的指派为cM（t）。如果语句φ中的每一个常项和变项在M中都有一个指派，那么我们说φ在M中被定义，用Def（M）表示M中被定义的语句集。如果模型M的定义域DM中的一个元素b在denM的值域中，那么我们说b在模型M中被命名。对于任意一个这样的b，我们使用去表示任意一个常量或变量在 M中的指派为 b。即，denM（）＝b，是任意一个常量或变量。需要注意的是，对于一个给定的b，是什么依赖于我们要考虑的模型M。即使M是一个固定的模型，也未必是唯一的。

定义2（全模型） 一个全模型是建立在一个部分模型M上并要求M中的元素LM满足下列条件：

（1）对LM中的任意n元关系符号R和M的定义域DM中的任意n个元素m1，…，mn组成的n元有序组〈m1，…，mn〉，〈m1，…，mn〉∈ExtM（R）∪AntiM（R）；

（2）LM中的每一个常项符号c在M中都有指派。

有两种扩大部分模型的方法。其一，是在保持部分模型M的定义域DM不变的基础上进行扩充；其二，是扩张部分模型的定义域DM。先看前者。

定义3 如果满足下列条件，则把模型M2称作模型M1的扩充，记作M1⊆M2：

（1）模型M1和模型M2的定义域相同；

（2）模型M1的语言是模型M2的语言的子集；

（3）对于每一个关系符号R∈LM1，R在M1中的外延和反外延分别是R在M2中的外延和反外延的子集；

（4）模型M1的指派函数是模型M2的指派函数的子函数；

（5）模型M1的语境是模型M2的语境的子函数。

用这种方法，可以将任意一个模型扩充成一个定义域保持不变的全模型。

定义4 如果模型M2是模型M1的扩张，记作M1M2，必须满足条件：

（1）模型M1的定义域是模型M2的定义域的子集；

（2）其他条件与M1⊆M2的相同。

有了模型，就需要考虑语句在模型中为真的问题。一个语句φ在全模型M中为真的定义，仍然采用的是标准赋值定义。一个语句φ在部分模型M中为真的定义，采用的是克里尼的三值赋值。

定义5（克里尼赋值） 对于模型M和M中定义的语句φ，定义M⊨φ和M⊨－φ如下：

如果φ是原子语句，即φ＝R（m1，…，mn），那么

M⊨ φ当且仅当〈m1，…，mn〉∈ExtM（R）；

M⊨ －φ当且仅当〈m1，…，mn〉∈AntiM（R）。

如果φ是合式语句，那么

M⊨ φ当且仅当M⊨－φ；

M⊨－ φ（当且仅当M⊨φ；

M⊨（ψ1ψ2）当且仅当M⊨ψ1M⊨ψ2；

M⊨－（ψ1ψ2）当且仅当M⊨－ψ1M⊨－ψ2；

命题1 如果M是一个全模型并且φ∈Def（M），那么M⊨ φ当且仅当Mφ。

证明：通过对语句φ的结构归纳证明可得，Mφ当且仅当M⊨－φ。由定义5，M⊨ φ当且仅当M⊨－φ，所以M⊨ φ当且仅当Mφ。

命题2 令模型M2是模型M1的扩充（或扩张）。如果M1⊨φ，那么M2⊨φ。类似地，如果M1⊨－φ，那么 M2⊨ －φ。

证明：通过对语句φ的结构归纳可证。

推论1 不存在模型M和语句φ使得M⊨φ并且M⊨－φ。

证明：用反证法。假定存在模型M和语句φ，使得M⊨φ并且M⊨－φ。令模型N是模型M的全扩充（或扩张），即N是一个全模型，由命题2可得，N⊨φ并且N⊨－φ。由定义5，M⊨ φ当且仅当M⊨－φ，可得，N⊨φ并且N⊨ φ。但是对全模型N，根据命题1，Nφ当且仅当N⊨ φ。这与N⊨φ并且N⊨ 相矛盾，所以假设不成立，命题得证。

如果M是一个部分模型，那么M⊨ φ和Mφ二者有很大的不同。例如，如果常量c在M中没有指派，那么R（c）在M中不为真，即MR（c）；同样，R（c）在 M中也不为假，即 M－R（c）。由定义 5，M⊨ R（c）等价于M⊨ －R（c）。

定义6 如果Mφ，那么语句φ在模型M中不为真。相反，如果M⊨ φ，那么语句φ在模型M中为假。

由上述定义可得，如果φ在模型M中为假，那么φ在模型M中不为真。这里，模型M既可以是部分模型，也可以是全模型。如果φ在模型M中不为真，那么φ在模型M中为假。这里，模型M只能是全模型。

模型的定义域中的元素可以是任何事物，尤其可以是本元、L的语句和L的模型。这就允许我们把语言限定为包含语义谓词的语言，像真谓词和指称谓词。巴威斯和莫斯受到可及世界和自返集合这两个概念的启发，给出了可及模型和自返模型的定义。

定义7 如果模型N是模型M的定义域DM中的一个元素，我们称模型N在模型M中是可及的。如果M可及自身，即M自身是其定义域中的元素，我们称模型M是自返的。

根据广义解引理，每一个模型都可以扩张为一个自返的全模型。

二、给语言增加真谓词

前面，我们建立了处理语义悖论的数学框架，因为要分析和真谓词有关的几个悖论，还需要在已有的语言中增加一个表示真的二元谓词：True。True（x，y）表示语句x在模型中y为真，通常将True（x，y）记作 Trueyx。对于一个固定的模型 M，用 True（a，b）表示〈a，b〉∈ExtM（True），False（a，b）表示〈a，b〉∈AntiM（True）。为了让谓词True表达“真”，可以增加如下条件：

如果M是一个全模型，那么对于所有的φ，N∈DM，

（T0）True（φ，N）当且仅当 N是一个模型，φ∈Def（N）并且 N⊨ φ。

条件（T0）是塔斯基T-模式的一个版本。如果M是一个部分模型，令（T1）是（T0）从左到右的方向，即：

（T1）如果 True（φ，N），那么 N是一个模型，φ∈Def（N）并且 N⊨ φ。

因为一个条件一定在True的外延中，所以条件（T1）总是成立。但是，True的反外延有两种可能性，即（T2）和（T3）。

（T2）如果 N是一个模型，φ∈Def（N），并且 False（φ，N），那么 N⊨ －φ。

（T3）如果 N是一个模型，φ∈Def（N），并且 False（φ，N），那么 Nφ。

如果 M和 N是全模型，那么（T2）和（T3）都等价于（T1）的逆。即，（T0）等价于（T1）和（T2）的合取，或者（T0）等价于（T1）和（T3）的合取。但是，如果M是部分模型，那么（T2）和（T3）这两个条件则有很大的不同。（T2）的意思是说“语句φ在模型N中为假”，（T3）的意思是说“语句φ在模型N中不为真”。

在《说谎者：论真和循环》一书中，巴威斯和艾克曼迪提出了关于悖论的两种不同的阐释，即罗素型阐释和奥斯汀型阐释。在这里，罗素型阐释对应于条件（T2），而奥斯汀型阐释则对应于条件（T3）。

定义8 令M是一个模型。

（1）对于所有的语句φ∈DM和所有的模型N∈DM，模型M如果满足条件（T1）和（T3），那么M是真值正确的（truth-correct）。

（2）如果M是真值正确的并且满足条件（T1）和（T3）的逆，那么M是一个真值完全（truth-complete）的模型。即，当N∈M并且 φ∈Def（N）时，N⊨ φ蕴含着True（N，φ），Nφ蕴含着 False（N，φ）。

可以看出，M是真值完全的当且仅当它满足条件（T0）。如果在M的定义域中只有全模型，那么条件（T2）和（T3）是等价的。这时，“为假”和“不为真”这两个概念是一致的。但是，对于定义域中包含非全模型的模型来说，“为假”和“不为真”这两个概念是不同的。

下面把“为假”和“不为真”这两个概念和塔斯基的T-模式做一比较：

语句是真的当且仅当S。

这里，指一个英语语句S。可以看出，塔斯基的T-模式无视条件（T2）和（T3）的区别。

塔斯基的T-模式隐含地假设世界是自返的，并且我们有在世界中讨论世界的方法。换句话说，T-模式隐含地假设我们有某个项指涉模型M自身。给定这样一个项，我们把True简记为 True（）。

命题3 令M是一个自返的模型，有一个项指派M自身，即denM（）＝M。对于任意的语句φ∈Def（M），φ在 M中有一个名字，即 denM（）＝φ。如果 M满足（T1）和（T1）的逆，那么True（）↔φ

证明：很容易证明，这里从略。

三、几个和真谓词有关的悖论

有了前面的工作做准备，下面我们以说谎者悖论、强化的说谎者悖论、佐丹卡片悖论为例，说明反基础模型论解悖方法的巧妙之处。为了方便，把谎言语句形式化为“ Trueh（this）”，这里True和h（指“here”）是指我们语言中的常量或变量。谎言语句的实际意思是“本语句在此模型中不是真的”，用反证法，可以证明下述谎言定理：

定理1（谎言定理） 令λ是谎言语句 Trueh（this）。如果M是一个真值正确的模型，那么至少下述三者之一不成立：

（1）This在M中的指派是λ；

（2）h在M中的指派是M；

（3）M⊨ λ λ。

特别地，如果（1）和（2）同时成立，那么M不是一个全模型。

证明：用反证法。假定（1）（2）和（3）同时成立，就会得到矛盾的结论。因为M⊨λ λ，根据定义5可得，M⊨ λ M⊨ λ。首先，假定 M⊨ λ，即 M⊨ Trueh（this），根据定义5可得，M⊨ －Trueh（this）。因为this在M中的指派是λ，h在M中的指派是M，由定义5，〈λ，M〉在True的反外延中。但是，由（T3），Mλ。Mλ与 M⊨ λ相矛盾。现在假定 M⊨ λ，即，M⊨ Trueh（this）。由定义5，〈λ，M〉在True的外延中，由（T1），M⊨ λ。M⊨ λ与 M⊨ λ相矛盾。所以（1）（2）和（3）不能同时成立。

因为（1）和（2）同时成立，所以（3）不成立。用反证法。假定M是一个全模型，所以〈λ，M〉要么在True的外延中，要么在True的反外延中。如果〈λ，M〉在True的外延中，根据（T1），M⊨λ。因为M是全模型，所以（T2）和（T3）是等价的。如果〈λ，M〉在 True的反外延中，根据（T2），M⊨－λ，由定义5可得，M⊨ λ。M⊨λ或者M⊨ λ，根据定义5可得M⊨λ λ。这与（3）不成立相矛盾。所以，如果（1）和（2）同时成立，M就不是一个全模型。

已经提出的说谎者悖论的大多数“解法”可以看作抛弃（1）（2）和（3）三者之一。塔斯基不允许语言中包含真谓词，所以语言层次理论使（1）成为不可能。真值间隙论认为世界是完全的，任何断言要么真要么不真，所以它放弃了（3）。语境敏感方案放弃了（2），其思想是认为忽略了语境的变动所以出现了悖论。h的指派在断定前和断定后是有所变动的。下面通过两个例子说明这种变动如何发生，并由此认为语境敏感对于解释说谎者悖论背后的直观推理似乎是有道理的。

例子1 首先，构造一个真值正确的模型M0，使M0尽可能地接近由谎言定理排除的模型，但是M0放弃了谎言定理中的条件（2）。构造的模型M0满足下列3个条件：

（1）This在 M0中的指派是 λ＝ Trueh（this）；

（2）M0是自返的并且有它自身的一个名字；

（3）M0是一个全模型。

由谎言定理，使它成为可能的是将有某个项而不是h在M0中的指派为M0。

令M0被定义如下：

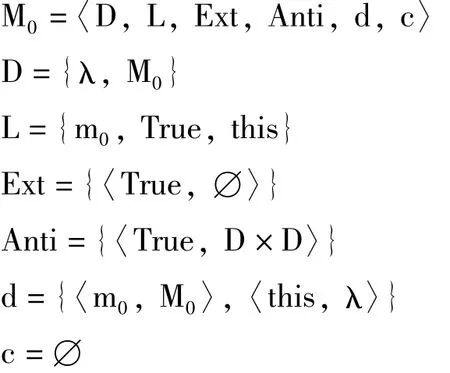
显然，模型M0有上述（1）（2）和（3）三个性质。可以看出，M0的定义域D中只有两个元素：λ和M0。可以在D中放入更多的元素，如x、y、z…，但是即使放入再多的元素，也没有什么用处。

需要注意的是，h在M0中没有指派，所以λ在M0中既不为真也不为假。由（T1），〈λ，M0〉在True的反外延中。

已经知道λ在M0中不为真，可以通过谎言语句 Truem0（this）这么做。因为 M0⊨ Truem0（this）。

在此，悖论消失了。因为有一个不同于λ＝ Trueh（this）的谎言语句λ′＝ Truem0（this），this在M0中的指派为 λ＝ Trueh（this）。

这个例子恰好回应了强化的说谎者悖论，然而并不完全是强化的说谎者悖论，因为语句从λ变为λ′。为了模型化强化的说谎者悖论，我们和最初的说谎者语句λ一样做出相同的断言。

例子2 构造一个真值正确的自返模型M1，并且使M1满足下列3个条件：

（1）This在 M1中的指派是 λ；

（2）h在 M1中的指派是M0；

（3）M1是一个全模型。

令M1被定义如下：

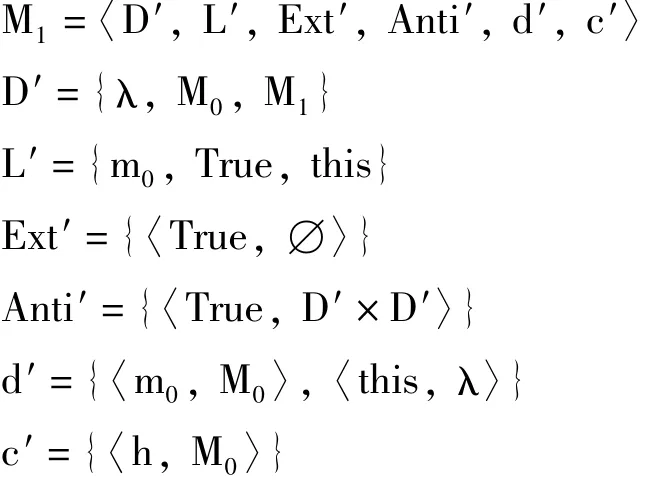
这里，模型M0是例子1中构造的模型。模型M0和M1是非常相似的，如果不在M1的语境c′中放入有序对〈h，M0〉，那么模型M0和M1是互模拟的，因此模型M0和M1是等同的。

例子3 构造一个满足下列3个条件的模型M2：

（1）This在 M2中的指派是 λ＝ Trueh（this）；

（2）h在 M2中的指派是M2；

（3）M2是一个真值正确的模型（但M2不是一个全模型，全模型的情况由谎言定理排除掉了）。

令M2被定义如下：

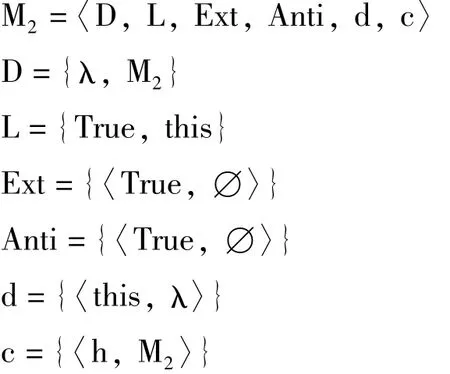
需要注意的是，M2是一个真值正确的自返模型，正如谎言定理预测的那样，M2既不使λ为真，也不使 λ为真。

再次看强化的说谎者悖论，这次使之与M2相联系。

例子4 存在一个满足下列3个条件的模型M3：

（1）This在 M3中的指派是 λ＝ Trueh（this）；

（2）h在 M3中的指派是M2；

（3）M3是一个真值正确的全模型。

令M3被定义如下：

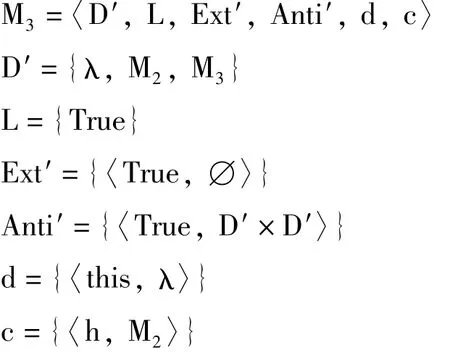
这里，悖论消失了，因为谎言语句不是关于模型M3的，而是最初的部分模型M2。用这种方法模型化事物，谎言语句就不是真的，但是强化的说谎者是真的。即，λ（和λ）在M2中不为真，但是λ在M3中为真。在谎言语句和扩展的谎言语句之间有一个语境的变化；它们同样是关于相同的模型M2，但是却是在模型M2和M2的扩张M3中被评价的。

例子5 令α＝Trueh1（that2），β＝ Trueh2（that1）。α表达的意思是“β语句在此模型中为真”。β表达的意思是“α语句在此模型中为假”。构造两个真值正确的全模型M4和M5，使得that2在M4中的指派是β，h1在M4中的指派是M4，that1在M5中的指派是α，h2在M5中的指派是M4。

令M4被定义如下：

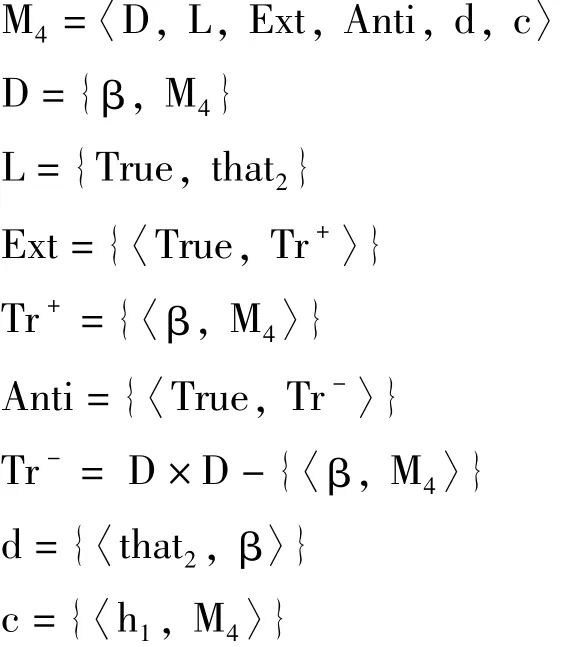
类似地，令M5被定义如下：

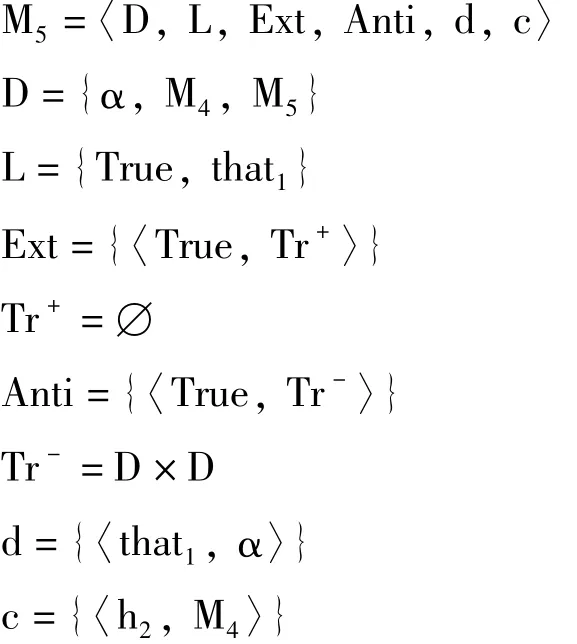
模型M4和M5都有想要的性质。

四、结语

可以看出，上文重点阐释和具体说明的反基础模型论解悖方法，不仅通过解释在不同情境中指派发生的变化以达到消解悖论的目的，同时还从侧面揭示了说谎者悖论产生的根源。由此可知，反基础模型论解悖方法对说谎者悖论进行处理的做法和情境语义学解悖方案有着相似之处。

本文主要讨论了在建构反基础模型论这一数学框架的基础上，通过给语言增加真谓词的方法，消解了几个包含真谓词的悖论。当然，用同样的方法，我们也可以分析诚实者语句、偶然的说谎者等与之类似的问题。同理，在巴威斯等所构造数学框架的基础上，我们还可以通过给语言增加指派谓词的方法，消解指称悖论，这也是笔者希望接着进行探讨的另一研究内容。