谈小学生运算能力的培养

苏巧真

一位初次教毕业班的青年教师问我，“在计算分数除法时，为什么有的学生“乱倒数”（被除数和除数都用它的倒数进行计算）？有时候被除数倒，除数不倒，有时候除号不变乘号，有时候乘法（的乘数）也在变倒数……”听着这位青年教师的话，我回忆起自己近十年教学毕业班的情景，班上都有若干个孩子出现上述情形，而且和同行交流时，也都有这种现象出现。于是，我们理所当然地认为是学生上课不认真听讲或遗忘造成的。但今年同样教学毕业班，在教学这个单元时，班上却没有一个孩子出现这种现象！细细回想，原因在于今年承担了一节《分数除以整数》的公开课，这节课经过较长时间的思考、实践，达到了较好的教学效果。在教学本课之前，经过细读教材和进行学生访谈，笔者思考了三个问题：一是这节课的计算方法较为简单，重点和难点是算理的教学，如何教才能让学生知其然并知其所以然？二是整数、小数、分数加减法的本质是相同计数单位相加减，乘法的本质是相同计数单位的累加，那么除法的本质是什么呢？分数除以整数与小数、分数除法在本质上一样吗？它们之间有什么联系和区别？三是计算是真的只要会算就行了吗？还应培养孩子哪些素养呢？笔者带着这些思考，经过实践，有了以下收获。

一、理解算理，掌握运算方法

算法、算理是运算能力的一体两翼，两者相辅相成，不可偏废。不掌握算法就无法确保实现运算能力的最低要求“正确”，只知怎样算，不知为什么这样算，充其量只是搬弄数字的操作技能。例如，在本课教学中，教师根据学生的已有认知，引导学生理解算理，迁移类推，在此基础上提升算法。

师：÷2，会算吗？想想，如何让大家看得懂你为什么这样算？在练习本上算一算、写一写。

生1： 里有4个，除以2，每份就有2个，也就是 。

生2：我的计算方法跟第一个同学一样，÷2= =，但想法不一样，我是想，分数乘法，是分母不变，分子相乘，所以，分数除法，应该也是分母不变，分子相除。

师：你用到了联想的方法，算除法想乘法。

生3：

÷2就是把 平均分成2份，每份占它的，也就等于×。

师：谁听明白他的意思了？老师把这个 请到黑板上来，谁再来说一说除以2为什么就是乘它的？

生：（边说边画），除以2就是把平均分成两份， ，这一份就是的 ，列式就是×。

师：同桌互相说说除以2为什么就是乘它的。

（画图只是手段，不是目的，其根本是为了建立操作过程与算理之间的联系，更好地让算理外显。关键时刻教师要善于想办法让学生摆脱直观的干扰和依附，变操作技能为心智技能。）

师：÷2大家不仅会算，而且还用了三种方法理解为什么这样算的道理。那÷3会算吗？

生：÷3=×=

生：÷3=÷3==

师：跟大家说说你是怎么想的？

生：因为分子4不能被3整除，我就把通分，变成 ，12可以被3整除。这其实是由÷2的第一种方法想到的。

生：（此时一位学生举起了手）老师，是不是所有的分数除以整数都可以用以上两种方法来做呢？（全班同学有的说“是”有的说“不一定”）

生：可以多举几个例子验证看看。

学生通过举例，发现了“一个数除以整数（0除外），等于乘这个数的倒数，可以用 ÷c= ×（a、c都不为0）”表示，还发现了“分数除以整数（0除外），如果分数的分子可以被整数整除，可以用分子除以整数的商做分子，分母不变;如果不能整除，把这个分数通分成分子是整数的倍数的分数，再用分子除以整数的商做分子，分母不变”。当教师引导学生对两种方法进行对比选择时，大部分学生选择了第一种，个别同学坚持第二种方法，部分同学选择“中间地带”，当分数的分子是整数的倍数时，用分子除以整数的商做分子，分母不变，当分数的分子不是整数的倍数时，则采用“一个数除以整数（0除外），等于乘这个数的倒数”的方法。

算理与算法构成运算能力的两翼。在以上教学中，教师引导学生利用直观、联系旧知等多种方式理解算理，并遵循着算理，发现算法、驾驭算法，巧妙地实现了算理与算法的有机融合。在此过程中，教师充分尊重学生的个性，允许学生保留自己喜欢的算法，真正做到了循理入法，以理驭法，培养学生的运算能力。

二、整体架构，厘清运算本质

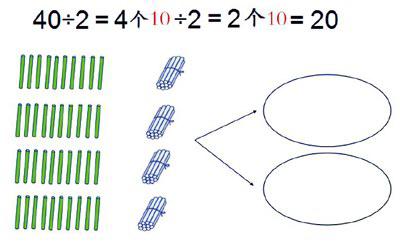
教师不仅要有从宏观上对数学知识整体结构的正确把握，更要把这种素养转化为对学生的培养，要引导学生对数学知识进行整体架构，沟通知识间的联系，凸显数学本质。数的运算隶属于“数与代数”领域，与数的认识联系紧密，在教学中，教师要引导学生突出对计数单位、位值制等核心概念的深入领会，从而沟通它们本质的联系。例如本课教学末，教师引导学生对整数除法、小数除法和分数除以整数的计算道理进行比较，有的学生认为它们的计算道理一样，有的认为不一样，在此基础上，教师借助“微课”（撷取其中几张画面）让学生在形象生动的画面中理解除法的本质——平均分，即把几个这样的计数单位进行平均分，分得每份是几个计数单位，就是几。

在以上教学中，教師把“分数除以整数”放在“除法”这一概念运算的范畴中进行教学，学生在理解“分数除以整数”的算理的基础上回忆整数除法、小数除法的计算道理，教师借助直观教学，从本质上沟通了三者之间的联系，让学生发现三者的计算道理是一样的，深化了对知识本质的理解。这样教学，从整体上进行建构，让学生既见“树木”，又见“森林”，有利于学生对算理的理解和算法的掌握，有助于提升学生的运算能力。

三、有效练习，提高运算水平

运算能力结构的刻画可用结构模型图来表示（见下图）。

对于小学生来说，基本口算反应与进一步的算法、算理共同构成运算能力的底部。运算能力的提高必须建立在这一基础上。运算策略是指运算信息的挖掘与运算问题的定向，运算方法的选择与运算过程的简化及其自觉评价。它表现在解决单纯的运算问题中，也表现在解决实际问题的运算决策与实施过程中。运算策略与其他三个要素相互关联，运算策略水平是鉴别运算能力的敏感因素。因此，在计算教学过程中，除了要引导学生理解算理，掌握算法外，还应培养学生灵活选择运算策略的能力，以期提高学生的运算能力。如本课教学中，在学生理解了算理、掌握了算法的基础上，教师出示以下练习：1.计算÷3、 ÷3、÷3、 ÷3、 ÷3 、÷3 ;2.为美化教室，同学们用彩带折纸花， 米可以折4朵纸花，照这样计算，米可以折多少朵纸花？

在学生的反馈中，第1题中前三题大部分学生采用“分子除以整数做分子，分母不变”的方法进行计算，后三题采用“分数乘整数的倒数”的方法进行计算。如此设计，旨在培养学生自觉根据运算信息，灵活选择运算方法的能力。第2题是这样解决的：有的列式÷4=（米），÷ =8（朵）;有的列式÷=2，4×2=8（朵）。÷和÷是分数除以分数的计算，学生还没学，但学生根据推理，把通分成，÷=8，同理可推出÷的结果。如此设计，不仅有利于学生靠理解算理和灵活选用算法来保证运算正确，而且激活了学生的思维，巧妙地将旧知与新知建立起联系，利用旧知学习新知，突出了运算思维的推理成分。

“课标2011年版”中指出：“运算能力主要是指能够根据法则和运算律正确进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。”言下之意，运算能力的培养，主要依靠根据法则和运算律提高正确性，通过理解算理与灵活运算解决问题，发展能力。为此，教师在进行教学时，应充分引导学生理解算理，掌握算法，掌握运算的本质，进行正确计算，并在此基础上精心设计练习，激活学生的运算思维，帮助学生灵活选择运算策略解决问题，培养学生的各种能力。