不同价态Mn掺杂InN电子结构、磁学和光学性质的第一性原理研究∗
徐大庆赵子涵李培咸王超张岩刘树林童军
1)(西安科技大学电气与控制工程学院,西安 710054)
2)(西安电子科技大学先进材料与纳米科技学院,西安 710071)
3)(西安微电子技术研究所,西安 710015)
(2017年11月22日收到;2018年1月19日收到修改稿)
1 引 言
在半导体中同时利用电子的电荷和自旋属性,把标准的微电子技术与自旋相关效应相结合,有可能实现包括自旋场效应晶体管、自旋激光器、自旋随机存储器等在内的各种新颖的半导体自旋电子器件.实现实用化半导体自旋电子器件的基本条件之一是在半导体材料和器件中实现室温自旋极化电子的高效注入.稀磁半导体(dilute magnetic semiconductors,DMSs)兼具半导体材料和磁性材料的性质,被认为是解决半导体自旋电子器件自旋极化电子高效注入难题的理想材料.目前,大多数DMSs材料的居里温度(TC)低于室温,因此研制具有室温铁磁性的DMSs是半导体自旋电子学领域研究的巨大挑战和重要目标[1].此外,由于DMSs的磁性形成机制尚存在争议,探讨DMSs磁性的起源和磁交换方式也是DMSs领域研究的一项重要任务.
InN作为一种重要的III族氮化物,具有高的电子迁移率和低的电子有效质量,在光电器件、高频率高速率器件和高功率微波器件等方面具有广泛的应用前景.研制基于III族氮化物InN的DMSs,可以在利用现有的III族氮化物半导体材料制备技术的同时,能有效、快速地与已有的III族氮化物半导体电子器件相结合制备集合电学、光学以及磁学特性的多种功能的新型半导体自旋电子器件.
近几年,有研究报道了在InN纳米结构和薄膜中存在室温铁磁性[2−6],也有研究机构对掺杂InN基DMSs体系进行了研究[7−10],虽然也报道了存在室温铁磁性,但材料的磁性起源及形成机制尚不明确,还有待深入研究.
过渡元素Mn离子在III-V族化合物半导体中大多数情况下以Mn2+(d5,S=5/2)价态存在[11,12],但在一定条件下,也可以Mn3+(d4,S=2)价态存在[13−15],而Mn2+和Mn3+性质的差异会对掺杂半导体材料的物理特性产生不同的影响.本文采用第一性原理方法对Mn2+,Mn3+分别掺杂InN的电子结构、能量、磁学以及光学性质进行了理论计算和比较分析,发现InN中过渡元素Mn离子价态的改变对材料的电子结构、能量、磁交换方式和光学性质有显著的影响.本文对III族氮化物InN基DMSs掺杂过渡元素的价态及其相关研究,有助于进一步揭示III族氮化物基DMSs磁有序的微观机理,为新型III族氮化物基DMSs及器件的研发奠定物理基础.
2 模型构建和计算方法
2.1 模型构建
计算所用的理想模型是InN纤锌矿结构,属于P63mc空间群,对称性为本研究所用晶胞是基于InN原胞建立的(3×3×2)超胞模型,掺杂时用Mn取代InN中的In.为研究Mn掺InN体系的晶体结构、稳定性以及判断磁性特征,分别构建了两个Mn原子替换两个In原子的三种相同掺杂量不同空间有序占位的In34Mn2N36超胞模型,如图1(a)—(d)所示.
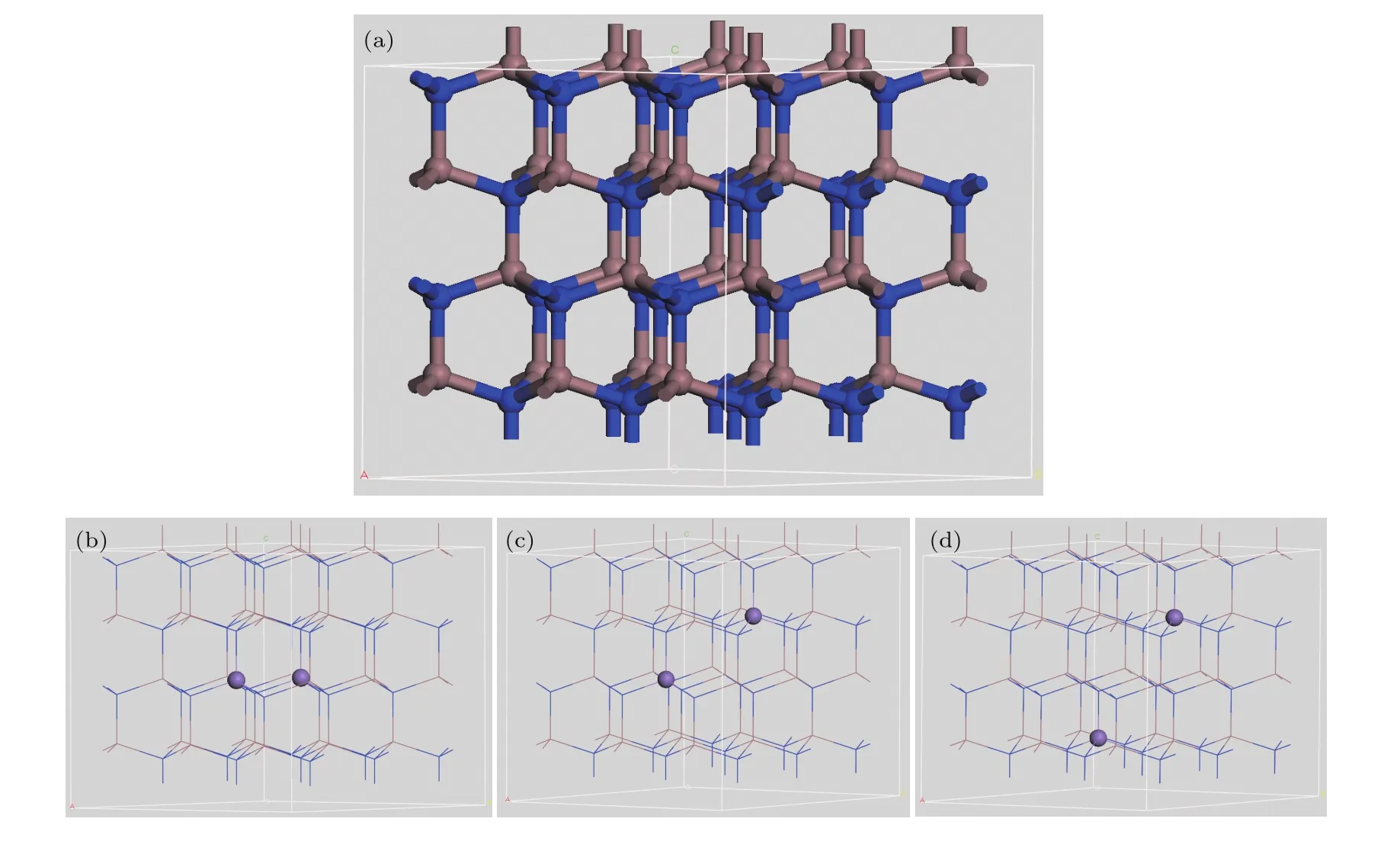
图1 (a)InN超晶胞的透视图及In34Mn2N36超晶胞的透视图;(b)结构I;(c)结构II;(d)结构IIIFig.1.(a)InN supercell and schematic structure of Mn double-doped InN;(b)configuration I;(c)configuration II;(d)configuration III(the blue,gray,purple spheres represent N,In and Mn atoms,respectively).
2.2 计算方法
采用基于密度泛函理论体系下的广义梯度近似(GGA+U)平面波超赝势方法的Castep软件[16],分别对未掺杂纤锌矿InN超胞和三种不同有序占位Mn2+/3+价态分别掺杂InN超胞模型进行几何结构优化和相关性能计算.在计算中,选取In,N和Mn原子的价电子组态分别为:In 4d105s25p1,N 2s22p3,Mn 3d54s2,截断能取350 eV,自恰收敛精度为1×10−6eV/atom,原子间相互作用力收敛标准为0.03 eV/nm,单原子能量的收敛标准为1.0×10−5eV/atom,晶体内应力收敛标准为0.05 GPa,原子的最大位移收敛标准为0.001 nm.因为广义梯度近似与局域密度近似在计算中往往低估总交换能,因此存在低估带隙的问题.计算通过引入Hubbard参数U(库仑作用能)来描述原子间强相关作用,所有体系中In的5p电子态和N的2p电子态分别取值U=4.0 eV和U=4.5 eV,Mn的3d电子态取值U=3.5 eV.
3 结果与讨论
3.1 体系结构和稳定性分析
为了研究Mn的不同价态对掺杂InN的影响,首先对未掺杂InN及Mn2+/3+价态分别掺杂InN的晶胞进行几何结构优化,计算中利用实验晶格参数先对InN超胞进行了几何结构优化,所得晶格结构参数与文献值的比较如表1所列.优化后c/a分别为1.6109,与文献[17]值1.6114符合得很好,偏差仅为0.3103‰,说明了本文计算方法的可靠性.可以看出Mn掺杂以+2价态存在时的超胞体积和晶格常数略有增大,这主要是由于Mn2+的离子半径为0.083 nm,略大于In3+的离子半径(0.081 nm),所以Mn2+掺入后会引起超胞体积和晶格常数有所增大.对于Mn掺杂以+3价态存在时,超胞体积和晶格常数则略有减小,这主要是Mn3+的离子半径为0.0645 nm,小于In3+的离子半径,所以Mn掺杂以+3价态存在时,会引起超胞体积和晶格常数减小.

表1 InN和Mn2+/3+价态分别掺杂InN晶格常数的优化计算值Table 1.The lattice parameters and volume of the pure and Mn doped InN after geometry optimized.
文献[10,18,19]报道,当Mn掺杂III族氮化物InN,GaN其掺杂量在0—10 at.%之内时,掺杂体系仍为纤锌矿结构,本文Mn掺杂InN,掺杂比例约为2.78 at.%,因此掺杂体系结构不会发生相变,满足本文限定的InN为纤锌矿结构的要求,这也保证了Mn掺杂InN计算结果的可靠性.
掺杂体系形成能是判断有序体系结构稳定性和掺杂难易程度的重要依据之一.为了说明Mn掺杂对InN体系稳定性和掺杂难易程度的影响,计算了不同空间有序占位Mn2+/3+价态分别掺杂InN的形成能,表达式如下[20]:
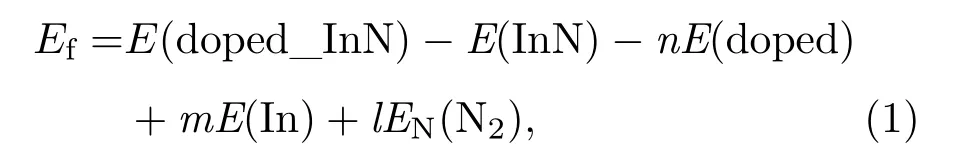
(1)式中,E(doped_InN)是掺Mn后的体系总能量,E(InN)是与掺杂体系相同大小的未掺杂InN超胞体系总能量,E(doped)和E(In)分别是Mn和In最稳定(基态)金属晶体的单个原子的能量,EN(N2)是N2分子中单个N原子的能量,n是掺杂Mn原子的个数,m是被替换In原子的个数,l是被替换N原子的个数.体系总能量和形成能的计算结果列于表2中.
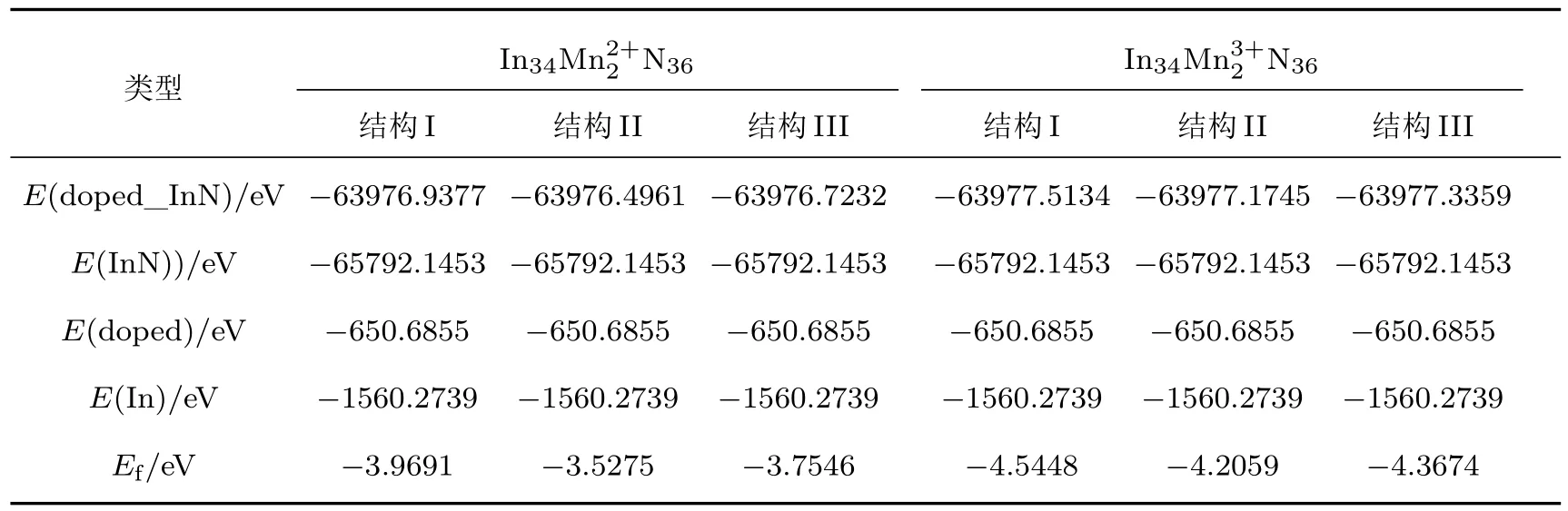
表2 不同空间有序占位Mn2+/3+价态分别掺杂InN的总能量和形成能Table 2.Total energies and formation energies for dif f erent systems of Mn2+/3+doped InN.
由表2可以看出,Mn2+掺入后三种不同有序占位双掺体系的形成能分别为−3.9691,−3.5275,−3.7546 eV,Mn3+掺入后形成能分别为−4.5448,−4.2059,−4.3674 eV,掺杂形成能越小,形成的结构越稳定、掺杂越容易.计算结果表明,Mn2+/3+价态分别替位In3+后掺杂体系都能够形成稳定的结构,与文献[8,10,18,21]报道的结果相符合.可以看出,与Mn2+掺杂InN相比较,Mn3+掺杂InN形成能更低,结构更稳定.
3.2 能带结构和态密度分析
利用几何优化后的晶体结构计算了未掺杂InN及Mn2+/3+价态分别掺杂InN的能带结构和态密度.图2(a)为InN的能带结构图.InN材料的带隙问题,虽然有文献报道认为其带隙为0.6—0.9 eV[22],而不是先前普遍接受的1.9 eV,但也有报道分析认为窄带隙是由InN中存在深的缺陷能级所造成的,InN的真正带隙约在1.25—1.30 eV[23].本文采用GGA+U的方法进行带隙修正,所得的带隙值约为 Eg=1.242 eV.图2(b)—(d)给出了InN的总态密度和分波态密度,从图中可以看到,InN的下价带主要是N的2s态、In的4d态及少量In的5s5p态和N的2p态贡献的;中价带主要是In的4d态、N的2s2p态及少量In的5s5p态贡献的;上价带主要是N的2p态、In的5s5p态及少量In的4d态和N的2s态贡献的.对于InN的导带部分,主要是来源于In的5s5p态和N的2s2p态的贡献.

图2 InN的能带结构和态密度图 (a)能带结构图;(b)InN总态密度;(c)In分波态密度;(d)N分波态密度Fig.2.(a)Energy band structure of InN;(b)total density-of-states DOS for InN;(c)partial DOS for In;(d)partial DOS for N.
图3 (a)和图3(b)为Mn2+掺杂InN的能带结构.掺杂后依然表现为直接带隙,并且能带结构变得更加紧密,这表明Mn2+掺杂使不同原子之间的相互作用增强.Mn2+掺杂后最显著的变化是能带图中位于价带顶上方出现了与Mn有关的自旋极化杂质带.从图3(a)和图3(b)中可以看出,费米能级与自旋上部分的能带相交,同时处于自旋下部分的能隙中.图3(c)—图3(f)为Mn2+掺杂InN的分波态密度以及In,Mn最邻近N和Mn的分波态密度.从图3(c)可以看出,自旋上和自旋下的总态密度呈现非对称性,这表明体系具有明显的自旋极化现象.由图3(c)并结合图3(d)—图3(f)可见,−15.6—−13.6 eV附近的峰值位主要来源于In的4d态和N的2s态,−13.4—−9.8 eV附近的峰值位主要来源于In的4d态和N 的2s2p态;−7.3—−0.5 eV附近的峰值主要来源于N的2p态、Mn的3d态、In的5s5p态以及少量In的4d态和N的2s态;−0.5—0.5 eV附近的峰值主要来源于Mn的3d态和N的2p态.可以看到,Mn的3d态与N的2p态有强烈的杂化效应.

图3 Mn2+掺杂InN的能带结构和态密度图 (a)自旋上能带结构;(b)自旋下能带结构;(c)Mn2+掺杂InN总态密度;(d)In的分波态密度;(e)Mn最邻近N的分波态密度;(f)Mn的分波态密度Fig.3.Energy band structure of Mn2+ions doped InN:(a)Spin up;(b)spin down and DOS curves for Mn-doped InN;(c)total DOS for Mn-doped InN;(d)partial DOS for In;(e)partial DOS for N nearest neighbor to Mn;(f)partial DOS for Mn.
图4 为Mn3+掺杂InN的能带结构和态密度图.由(图4(a)和图4(b)能带结构图)可以看到,与Mn2+掺杂InN相同,Mn3+掺杂后能带结构变得更加紧密,费米能级与自旋上部分的能带相交,同时处于自旋下部分的能隙中.能带结构图显示Mn3+价态掺杂体系发生了半导体-金属性转变,表现为半金属性.由图4(c)并结合图4(e)—(f)可见,与Mn2+价态掺杂体系态密度不同之处主要体现在位于价带顶上方与Mn有关的自旋极化杂质带明显展宽,且峰的强度明显减弱,同时位于价带底部的Mn的自旋上峰和位于导带底部Mn的自旋下峰均显著增强.
通常用p-d交换相互作用和双交换相互作用两种机制解释DMSs的铁磁性起源,但很难将某个DMSs毫无疑义地分类到一种磁交换相互作用机制中,而这两种交换相互作用对DMSs磁性主导作用的相对重要性取决于体系的电子结构,尤其是掺杂过渡元素d电子态的分裂分布以及杂质能带与费米能级的相对位置[24−26].对于Mn2+/3+价态掺杂InN,从Mn的分波态密度(如图3(f)和图4(f)所示)可以看到,由于交换劈裂使得Mn的3d态分裂为深入价带的上自旋态和深入导带的下自旋态,在晶体场和轨道杂化的作用下,过渡元素Mn离子的3d轨道进一步分裂形成了位于价带中的成键tb态和位于禁带中费米能级附近的反键ta态以及位于tb态和ta态之间的e态.这表明Mn掺杂InN中p-d交换相互作用和双交换相互作用在磁交换中起着重要作用.

图4 Mn3+掺杂InN的能带结构和态密度图 (a)自旋上能带结构;(b)自旋下能带结构;(c)总态密度;(d)In的分波态密度;(e)Mn最邻近N的分波态密度;(f)Mn的分波态密度Fig.4.Energy band structure of Mn3+ions doped InN:(a)Spin up;(b)spin down and DOS curves for Mn-doped InN;(c)total DOS for Mn-doped InN;(d)partial DOS for In;(e)partial DOS for N nearest neighbor to Mn;(f)partial DOS for Mn.
3.3 磁性分析
为了进一步分析掺杂体系的磁学特性,计算了不同空间有序占位Mn2+/3+价态分别掺杂InN样品的铁磁(FM)与反铁磁(AFM)的总能量、每个磁性过渡元素原子AFM与FM的相对能量差∆E=(EAFM−EFM)/2和总磁矩,计算结果如表3所列.

表3 不同空间有序占位Mn2+/3+价态分别掺杂InN的AFM和FM总能量、总能量之差和总磁矩Table 3.Total energies of AFM and FM,dif f erence of total energies and total magnetic moments for dif f erent systems of Mn2+/3+doped InN.
由平均场近似所给出DMSs的居里温度(TC)可近似表示为[24]

其中,kB为玻尔兹曼常数,TC是估算DMSs的居里温度,∆E是每个磁性过渡元素原子AFM与FM之间的能量差.从(2)式可见,∆E越大,TC亦越大.计算结果显示不同空间有序占位Mn2+/3+价态分别掺杂InN体系中,Mn2+双掺杂体系的E均小于热能kBT(30 meV)[27],而三种不同空间有序占位Mn3+双掺杂InN的E均大于零,且结构I和III空间有序占位Mn3+双掺杂InN的E大于热能kBT(30 meV),这表明对Mn掺杂InN体系而言,Mn掺杂的不同价态和空间有序占位对形成稳定的铁磁有序有着明显的影响,当Mn掺杂以+3价态存在时有利于掺杂体系形成稳定的铁磁有序,也预示着有可能获得Mn掺杂InN体系的室温铁磁性.这与文献[10,18]报道的结果相符合.
图5和图6分别为三种不同空间有序占位Mn2+和Mn3+价态掺杂InN中Mn的分波态密度.对比图5和图6可以看出,Mn以+3价态存在时位于价带底的自旋上tb态明显增强,尤其是位于导带底的自旋下态显著增强.计算表明(如表4所列),三种不同空间有序占位掺杂体系中Mn3+价态掺杂的tb/ta峰强比明显大于Mn2+价态掺杂的tb/ta峰强比.这表明在Mn3+价态掺杂InN中p-d交换相互作用对磁性能的主导作用强于Mn2+价态掺杂,由于p-d交换相互作用主导下材料居里温度与过渡元素掺杂浓度成正比,而双交换相互作用主导下材料居里温度与过渡元素掺杂浓度的开方成正比[24],因此在同样掺杂浓度下Mn以+3价态存在时材料更容易获得高的居里温度.这与3.2节的计算结果相一致.

图5 Mn2+双掺杂InN不同空间有序占位Mn的分波态密度 (a)结构I;(b)结构II;(c)结构IIIFig.5.Partial DOS curves for Mn of Mn2+doped InN:(a)Configuration I;(b)configuration II;(c)configuration III.

图6 Mn3+双掺杂InN不同空间有序占位Mn的分波态密度 (a)结构I;(b)结构II;(c)结构IIIFig.6.Partial DOS for Mn of Mn3+doped InN:(a)Configuration I;(b)configuration II;(c)configuration III.

表4 不同空间有序占位Mn2+/3+价态掺杂InN中Mn的3d电子成键态tb、反键态ta峰强及峰强比Table 4.Peak intensity and peak intensity ratio of Mn 3d electronic bonding state tband anti-bonding state tafor dif f erent orderly placeholder Mn2+/3+doped InN.
该发现对于通过控制掺杂过渡元素价态调节主导掺杂体系磁性能的磁交换相互作用,实现对材料磁性能的调控提供了一个新的研究方向,也将有助于进一步揭示III族氮化物基DMSs磁有序的微观机理,为新型III族氮化物基DMSs及器件的研发奠定物理基础.
3.4 光学特性
通过研究固体中的光吸收和光发射,可以获得有关固体中的电子状态、杂质缺陷态等多方面的信息.半导体的宏观光学性质可由与固体的电子结构相联系的复介电函数ε=ε1(ω)+iε2(ω)来描述,介电函数的虚部ε2(ω)可以通过计算电子在能带间的跃迁得到,介电函数实部ε1(ω)可利用Krames-Krönig关系由ε2(ω)推得,其他诸如吸收系数α(ω)、反射率R(ω)、折射率n(ω)和损失函数L(ω)等光学常数均可由ε1(ω)和ε2(ω)推算得到[28,29]:
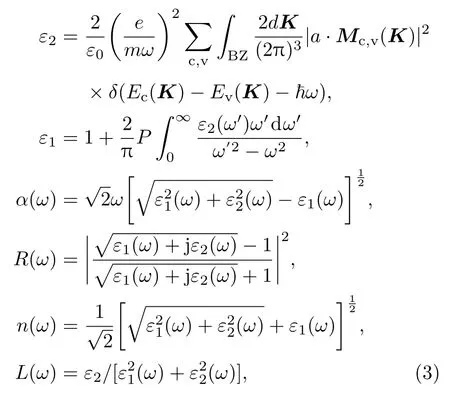
式中下标c,v分别表示导带和价带,BZ为第一布里渊区,K为倒格矢,|Mc,v(K)|为动量矩阵元,Ec(K)和Ev(K)分别为导带和价带的本征能级.
3.4.1 复介电函数
图7为计算所得Mn掺杂前后InN的介电函数实部ε1(ω)和虚部ε2(ω). 从图7(a)中可以看出,未掺杂InN的介电函数虚部ε2(ω)出现五个峰值.从态密度图能够看出,其中2.168 eV处的峰主要源于N-2p和In-5p(上价带)到In-5s和N-2s2p(导带底)之间的跃迁,3.443 eV处的峰主要是由于In-5p和N-2p(上价带)到N-2s2p和In-5s5p(下导带)之间的跃迁引起的,4.8152 eV处的峰主要是来自In-5p和N-2p(上价带)到In-5s5p和N-2s2p(中导带)以及In-5p和N-2p(上价带)到In-5s5p和N-2s2p(下导带)之间的跃迁,10.3341 eV处的峰主要是来自In-5s和 N-2p(上价带)到In-5s5p和N-2s2p(上导带)之间的跃迁,16.113 eV处的峰主要来源于In-4d和N-2s(中价带)到In-5s5p和N-2s2p(上导带)间的跃迁以及N-2s和In-4d(下价带)到In-5s5p和N-2s2p(下导带)之间的跃迁.与未掺杂InN相比可知,Mn的掺入使得InN的介电常数实部ε1(0)显著增大,且随着光子能量的增加迅速减小;对于Mn2+掺杂InN和Mn3+掺杂InN,介电函数虚部ε2(ω)曲线在高能范围(2—25 eV)和未掺杂InN的情形基本一样,而在低能范围内(0—2 eV)和未掺杂InN存在较大差异.Mn2+掺杂InN介电函数的虚部ε2(ω)在0.1656 eV左右,Mn3+掺杂InN介电函数的虚部ε2(ω)在0.2838 eV左右分别出现一强的新峰,其中Mn2+掺杂InN在0.1656 eV处峰值达到16.025,明显高于Mn3+掺杂InN在0.2838 eV处的峰值2.72.从能带结构和态密度图(图3和图4)可以看到,由于Mn 3d电子态和N 2p电子态之间强烈的杂化效应,在费米能级附近形成新的自旋极化杂质带,并且Mn3+掺杂InN中形成该自旋极化杂质带的Mn 3d电子态和N 2p电子态在费米能级附近的峰值强度明显弱于Mn2+掺杂对应峰的峰强.分析认为Mn2+掺杂及Mn3+掺杂InN介电函数虚部ε2(ω)在低能区分别出现的新峰可能主要来自价带顶与自旋极化杂质带之间的跃迁.

图7 介电函数实部和虚部 (a)未掺杂InN;(b)Mn2+双掺InN;(c)Mn3+掺杂InNFig.7.The real part and the imaginary part of the dielectric function of(a)the pure InN and(b)Mn2+doped InN,(c)Mn3+doped InN were calculated,respectively.
3.4.2 吸收光谱
图8 为未掺杂InN及Mn2+,Mn3+分别掺杂InN的吸收系数与能量的关系.对未掺杂InN,可以看到在能量低于1.021 eV的范围,对光的吸收损失为零.当光子能量大于1.021 eV后,吸收系数开始逐渐增大.在6.556 eV处吸收系数达到最大峰值.在能量为10.553 eV处出现第二个吸收峰,在能量为16.445 eV处出现第三个吸收峰.吸收谱的特征与介电函数虚部与能量的关系基本一致.对比InN和Mn2+/3+分别掺杂InN的吸收系数,可以看到Mn2+掺杂后体系在0.9380 eV处出现吸收峰,Mn3+掺杂后体系在0.8305 eV处出现吸收峰,这两个峰是未掺杂InN所没有的,其中Mn2+掺杂InN在0.9380 eV处的峰值达到27175,明显高于Mn3+掺杂InN在0.8305 eV处的峰值8231.分析认为,对于Mn2+,Mn3+分别掺杂InN,在0.9380 eV和0.8305 eV出现的吸收峰可能主要源于费米能级附近自旋极化杂质带和导带之间的跃迁.对于Mn3+掺杂InN,由于位于价带顶上方费米能级附近与Mn有关的自旋极化杂质带相对于Mn2+掺杂InN对应的杂质带向导带方向展宽了约0.1 eV,同时自旋极化杂质带的强度也明显降低,使得Mn3+掺杂InN中对应的吸收峰位移至0.8305 eV,且强度显著降低.
研究结果表明,Mn掺杂后体系的静态介电函数显著增大,掺杂体系介电函数虚部和吸收光谱在低能区分别出现了较强的新峰,结合能带结构和电子态密度分析,认为这主要是由与Mn掺杂在费米能级附近所产生的自旋极化杂质带相关的跃迁所致.这与文献[11,30,31]关于III-V族化合物中Mn掺杂杂质能级的报道分析相符合.从计算结果可以看出,Mn2+掺杂与Mn3+掺杂InN材料介电函数虚部和吸收光谱分别在低能区出现的新峰峰位几乎一致,但与Mn3+掺杂InN相比较,Mn2+掺杂InN材料介电函数虚部低能区出现的新峰峰值增大近6倍,吸收光谱低能区出现的新峰峰值增大3倍多,这表明Mn2+掺杂InN材料相应的光学效率更高,此发现对一定的InN基光学器件有潜在的应用前景.
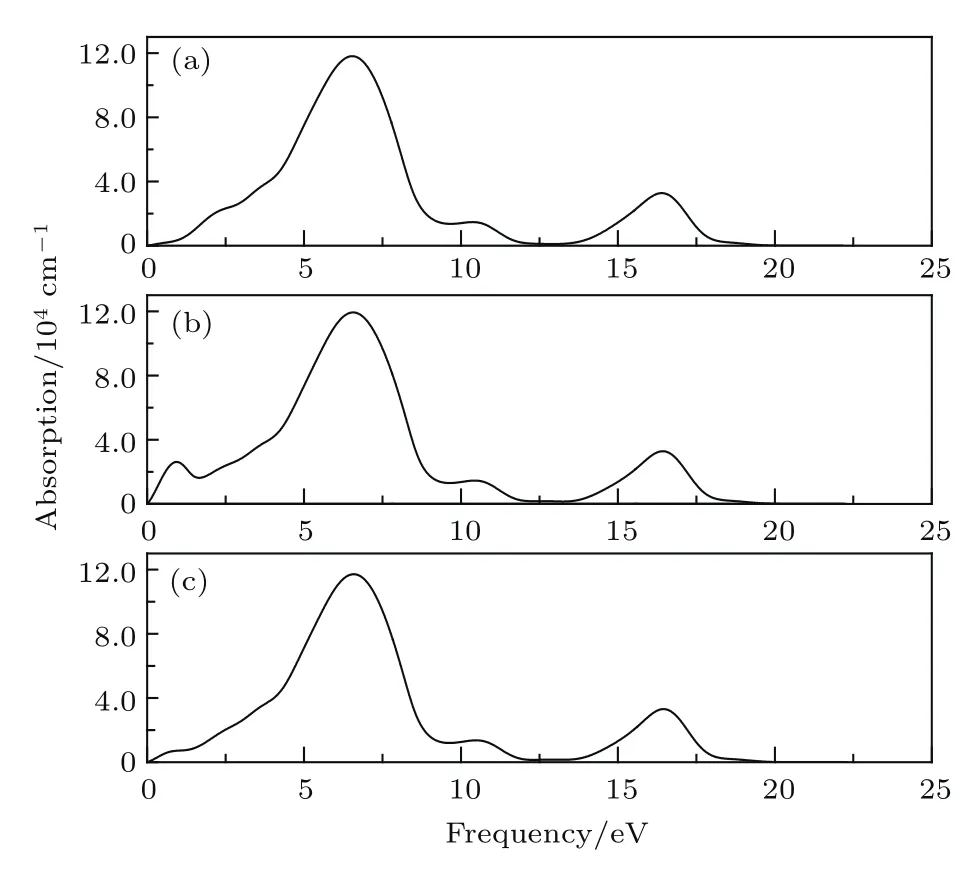
图8 吸收系数 (a)未掺杂InN;(b)Mn2+掺杂InN;(c)Mn3+掺杂InNFig.8.Absorption of(a)the pure InN and(b)Mn2+doped InN,(c)Mn3+doped InN were calculated,respectively.
4 结 论
采用基于密度泛函理论的平面波超软赝势方法,结合GGA+U计算了未掺杂纤锌矿InN超胞、三种不同有序占位Mn2+,Mn3+分别掺杂InN的电子结构、能量以及光学性质.研究表明,掺杂后体系总能量和形成能降低,稳定性增加,掺杂不同价态的Mn元素对体系电子结构、磁学和光学性质产生了不同的影响.电子结构分析表明,由于Mn 3d电子态和N 2p电子态之间强烈的杂化效应,在费米能级附近引入自旋极化杂质带,掺杂体系具有明显的自旋极化现象.磁性分析认为掺杂体系中的磁性来源于p-d交换机制和双交换机制的共同作用,Mn3+价态掺杂增强了p-d交换相互作用的主导作用,在同样掺杂浓度下Mn以+3价态存在有利于掺杂体系获得高的居里温度.与未掺杂InN相比,掺杂后体系的静态介电函数显著增大,掺杂体系介电函数虚部和吸收光谱在低能区分别出现了较强的新峰,分析认为介电函数虚部和吸收光谱中的新峰正是由于与费米能级附近自旋极化杂质带相关的跃迁所致.
[1]Dietl T,Ohno H 2014Rev.Mod.Phys.86 187
[2]Roul B,Kumar M,Bhat T N,Rajpalke M K,Krupanidhi S B,Kumar N,Sundaresan A 2014J.Nanosci.Nanotechnol.4 1
[3]Meng X Q,Chen Z H,Chen Z,Wu F M,Li S S,Li J B,Wu J Q,Wei S H 2013Appl.Phys.Lett.103 253102
[4]Ren M,Li M,Zhang C,Yuan M,Li P,Li F,Ji W,Liu X 2015Physica E67 1
[5]Caliskan S,Hazar F 2015Superlattices Microstruct.84 170
[6]Zhang K C,Li Y F,Liu Y,Zhu Y 2015J.Alloys Compd.625 101
[7]Fan S W,Huang X N,Yao K L 2017J.Appl.Phys.121 073905
[8]Chang P H,Chen H C,Lin J W,Lai M X,Hung S Y,Lee M J 2016Thin Solid Films618 184
[9]Alsaad A,Qattan I A 2014Physica B432 77
[10]Chen P P,Makino H,Yao T 2004Physica E21 983
[11]Wolos A,Palczewska M,Zajac M,Gosk J,Kaminska M,Twardowski A,Bockowski M,Grzegory I,Porowski S 2004Phys.Rev.B69 115210
[12]Graf T,Gjukic M,Hermann M,Brandt M S,Stutzmann M 2003Phys.Rev.B67 165215
[13]Graf T,Gjukic M,Hermann M,Brandt M S,Stutzmann M,Görgens L,Philipp J B,Ambacher O 2003J.Appl.Phys.93 9697
[14]Dalpian G M,Wei S H 2005J.Appl.Phys.98 1019
[15]Stefanowicz W,Sztenkiel D,Faina B,et al.2010Phys.Rev.B81 1601
[16]Zakrzewski T,Boguslawski P 2016J.Alloys Compd.664 565
[17]Zubrilov A 2001Properties of Advanced Semiconductor Materials GaN,AlN,InN,BN,SiC,SiGe(New York:John Wiley&Sons,Inc)pp49–66
[18]Alsaad A,Qattan I A 2011Physica B406 4233
[19]Kunert G,Dobkowska S,Li T,Reuther H,Kruse C,Figge S,Jakiela R,Bonanni A,Grenzer J,Stefanowicz W,Borany J,Sawicki M,Dietl T,Hommel D 2012Appl.Phys.Lett.101 022413
[20]Cui X Y,Medvedeva J E,Delley B,Freeman A J,Newman N,Stampf lC 2005Phys.Rev.Lett.95 256404
[21]Katayama-Yoshida H,Sato K 2003J.Phys.Chem.Solids64 1447
[22]Monemar B,Paskova P P,Kasic A 2005Superlattices Microsturct.38 38
[23]Briot O,Maleyre B,Ruf f enach S,Gil B,Pinquier C,Demangeot F,Frandon J 2004J.Cryst.Growth269 22
[24]Sato K,Bergqvist L,Kudrnovský J,Dederichs P H,Eriksson O,Turek I,Sanyal B,Bouzerar G,Katayama-Yoshida H,Dinh V A,Fukushima T,Kizaki H,Zeller R 2010Rev.Mod.Phys.82 1633
[25]Sato K,Katayama-Yoshida H 2012J.Non-Cryst.Solids358 2377
[26]Xu D Q,Li P X,Zhang Y M,Lou Y L,Li Y C 2016Thin Solid Films616 573
[27]Gopal P,Spaldin N A 2006Phys.Rev.B74 094418
[28]Sun J,Wang H T,He J L,Tian Y J 2005Phys.Rev.B71 125132
[29]Sahin S,Ciftci Y O,Colakoglu K,Korozlu N 2012J.Alloys Compd.529 1
[30]Graf T,Gjukic M,Brandt M S,Stutzmann M,Ambacher O 2002Appl.Phys.Lett.81 5159
[31]Titov A,Biquard X,Halley D,Kuroda S,Bellet-Amalric E,Mariette H,Cibert J,Merad A E,Merad G,Kanoun M B,Kulatov E,Uspenskii Y A 2005Phys.Rev.B72 115209

