绝缘层上单轴应变硅的应力计算与分析
苗东铭, 戴显英, 吴淑静, 赵天龙,邵晨峰, 郝 跃
(1. 西安电子科技大学 微电子学院,陕西 西安 710071;2. 西安电子科技大学 宽带隙半导体国家重点学科实验室,陕西 西安 710071)
绝缘层上单轴应变硅的应力计算与分析
苗东铭1,2, 戴显英1,2, 吴淑静1,2, 赵天龙1,2,邵晨峰1,2, 郝 跃1,2
(1. 西安电子科技大学 微电子学院,陕西 西安 710071;2. 西安电子科技大学 宽带隙半导体国家重点学科实验室,陕西 西安 710071)
为了研究晶圆级绝缘体上单轴应变硅的应力分布与应力变化趋势,首先利用绝缘体上硅晶圆在机械弯曲状态下退火的工艺,成功制作了绝缘层上单轴应变硅晶圆,其优点是工艺简单、成本低、应变量高.应用ANSYS仿真软件,重点对不同弯曲半径、不同晶向的机械致绝缘层上单轴应变硅晶圆的应力情况进行了模拟计算.模拟结果表明,应力随弯曲半径的减小而显著增加,且沿弯曲方向的应力最大,适于作为应变互补金属氧化半导体器件的沟道方向,但应力分布的均匀性会随弯曲半径的减小而略有下降.最后利用光纤光栅法对制备的绝缘层上单轴应变硅晶圆的应力分布进行了测量,其结果与ANSYS模拟结果吻合,证明了ANSYS模拟分析的准确性.
机械弯曲退火;晶圆级单轴应变;绝缘体上硅;应力分布;有限元分析
绝缘层上应变硅(strained Silicon-On-Insulator,sSOI)是兼具绝缘体上硅(Silicon-On-Insulator,SOI)与应变硅优点的具有创新与竞争力的前沿技术,可用于实现高速、低功耗集成电路[1-4].传统sSOI的制备是在绝缘层上锗硅(Si1-xGex-On-Insulator,SGOI)晶圆上外延生长Si,但只能制备双轴应变的sSOI,且其存在位错密度高、SiGe虚衬底影响器件和电路的散热、Ge的扩散影响工艺集成等问题,特别是空穴迁移率增强效应会在高场下退化[5].
单轴应变较之于双轴应变,其电子和空穴的迁移率增强效益在高电场下不退化,阈值电压漂移小,且在相同应变量下,单轴应变产生的迁移率增强效应更为显著.文献[6-8]的结果表明,单轴应变量即使低于0.05%,硅载流子迁移率的增强效应也可以达到15%.
基于绝缘体上硅材料的力学特性和弹性力学理论,笔者提出了利用单片绝缘体上硅晶圆、通过机械弯曲与退火工艺制作晶圆级单轴应变绝缘体上硅的新方法[9-10].在此研究基础上,采用有限元分析软件ANSYS,系统计算分析了单轴应变绝缘体上硅晶圆的应力和应变分布情况.利用光纤光栅法,对单轴应变绝缘体上硅晶圆的应力分布进行了测试表征,并与ANSYS模拟结果进行了分析对比.

图1 机械致单轴应变绝缘体上硅晶圆有限元模型
1 工艺原理与有限元模型建立
利用弧形弯曲台,通过圆柱形压杆将绝缘体上硅晶圆顶层Si朝上,使其贴服于弯曲台弧面,并在弯曲状态下放置于退火炉中高温热退火,制备单轴应变绝缘体上硅晶圆.根据弹性力学理论,当绝缘体上硅晶圆受压杆作用贴服于弧形弯曲台时,中性面之上的顶层Si沿弯曲方向产生拉伸作用,故晶格常数增大.由于SiO2的屈服强度为 8.4 GPa,小于单晶Si的 12.8 GPa,在一定弯曲退火工艺中,若使施加的外力超过SiO2的屈服强度而小于单晶Si的屈服强度,则使埋氧化层发生塑性形变,而单晶Si为弹性形变,这样绝缘体上硅从弯曲台卸下后,其埋氧化层在绝缘体上硅晶圆恢复原状后仍保持一定的拉持作用,使其上的顶层Si产生张应变,形成单轴张应变绝缘体上硅晶圆.
根据ANSYS软件的设置要求和弯曲台结构,定义了单晶Si、SiO2薄膜的材料参数与绝缘体上硅晶圆的材料结构尺寸,建立了机械致单轴应变绝缘体上硅晶圆弯曲退火装置的ANSYS结构模型,如图1所示.由于对称性的缘故,只建立了 1/4 模型,可减少计算量,节省计算时间,但并不影响模型的准确性.
2 ANSYS模拟结果与分析
对单轴张应变与压应变绝缘体上硅晶圆在室温下的应力与应变分布进行了ANSYS仿真,曲率半径分别为 1.00 m、0.75 m、0.5 m,对应的施加载荷分别为 260 N、295 N、408 N.
2.1 张应变绝缘体上硅晶圆应力分布
在弯曲半径为1 m的情况下,张应变绝缘体上硅晶圆顶层Si中应力沿x、y、z方向的分布分别如图2(a)~(c)所示,其中x方向为垂直于弯曲面的方向,y方向为弯曲方向,z方向平行于弯曲面并与x方向垂直.由图可见,其应力分布均匀,只有在压杆处(外力施加处)出现了较大波动,这是圣维南效应所致.因此采用该方法制成的绝缘体上硅晶圆片完全可以应用到集成电路器件制造工艺中.

表1 单轴张应变绝缘体上硅顶层Si在不同弯曲半径下各方向的应力
图2(d)~(f)给出了在1.00 m、0.75 m和0.50 m弯曲半径下张应变绝缘体上硅晶圆顶层Si沿y方向的应力分布.在 1.00 m 和 0.75 m 弯曲半径下的应力分布比 0.50 m 弯曲半径下的应力分布均匀,表明弯曲度越大,应力分布越不均匀.表1中给出了 1.00 m、0.75 m 和 0.50 m 弯曲半径下单轴张应变绝缘体上硅晶圆4个位置点处的应力对比,由表可知,弯曲方向(y方向)的应力随弯曲半径的减小而增加.

图2 单轴张应变绝缘体上硅顶层Si在1.00m弯曲半径下各方向以及不同弯曲半径下y方向的应力分布
图3 4个点的选取位置示意图
为了直观地分析绝缘体上硅晶圆顶层Si上应力的分布,选取了如图3所示的4个位置点处的应力数值,如表1所示.y方向(弯曲方向)与z方向的应力为正值,表明为张应力; 而x方向(垂直弯曲面)的应力值为负,说明x方向发生了相应的压应变.与x和z方向的应力比较可知,沿着弯曲方向的应力最大,约为108量级.所以,在设计制作互补金属氧化物半导体(Complementary Metal-Oxide-Semiconductor,CMOS)器件与集成电路时,应选用y方向(弯曲方向)作为沟道方向.
图4为单轴张应变绝缘体上硅中SiO2埋绝缘层在1.00 m弯曲半径下沿不同方向以及不同弯曲半径下y方向的应力分布.由图可见,在 1.00 m 弯曲半径下,SiO2埋绝缘层应力沿x、y、z方向的应力分布与单轴张应变绝缘体上硅晶圆顶层Si应力

图4 单轴张应变绝缘体上硅中SiO2埋绝缘层在1m弯曲半径下不同方向以及不同弯曲半径下y方向的应力分布
分布类似,只是在数值上较小,这是因为SiO2埋绝缘层和顶层Si一样,都处于中性面之上.在 1.00 m、0.75 m 和 0.50 m 弯曲半径下,SiO2埋绝缘层y方向的应力分布也与图2所示的顶层Si在不同弯曲半径下y方向的趋势相同,即应力随弯曲半径的减小而增加,而应力的均匀性却随弯曲半径的减小而降低.
2.2 压应变绝缘体上硅晶圆应力与应变分布
同样,对压应变下绝缘体上硅晶圆顶层Si应力分布进行了模拟,发现其应力分布趋势与单轴张应变的应力分布一致.表2给出了不同弯曲半径下单轴压应变绝缘体上硅晶圆顶层Si的4个点位置处的应力情况.y方向(弯曲方向)的应力为负值,表明为压应力; 而x方向的应力值为正,说明x方向发生了相应的张应变; 与x和z方向的应力相比,沿着弯曲方向的应力最大,约为107量级.与张应变的情况类似,在 1.00 m、0.75 m 和 0.50 m 弯曲半径下,单轴压应变绝缘体上硅晶圆顶层Si的y方向的应力分布也遵循相同的规律,即应力的大小及其分布的不均匀性随弯曲半径的减小而增加,如表2中结果所示.

表2 单轴压应变绝缘体上硅顶层Si在不同弯曲半径下各方向的应力
图5是单轴压应变绝缘体上硅中SiO2埋绝缘层在1.00 m弯曲半径下不同方向以及 1.00 m、0.70 m 和 0.50 m 弯曲半径下y方向的应力分布,其分布趋势与相同条件下单轴张应变绝缘体上硅晶圆SiO2埋绝缘层的分布趋势一致.而由图5(d)~(f)可见,在 1.00 m、0.75 m 和 0.50 m 弯曲半径下,单轴压应变绝缘体上硅晶圆SiO2埋绝缘层沿y方向的应力分布同样遵循应力随弯曲半径的减小而增加、应力的均匀性却随弯曲半径的减小而降低的规律.

图5 单轴压应变绝缘体上硅中SiO2埋绝缘层在1.00m弯曲半径下不同方向以及不同弯曲半径下y方向的应力分布
3 ANSYS结果与光纤光栅测试结果对比
为了验证应力有限元模型的准确性和应力计算的准确性,在5.3℃下进行了单轴应变绝缘体上硅晶圆应力的光纤光栅实验.根据胡克定律,若沿光纤平行的方向施加拉力F,光纤产生的轴向应变为
εz=(1/E) (F/S) ,
(1)
其中,E为光纤的杨氏模量,S为光纤截面积.而均匀轴向应变引起的波长漂移为

ΔλB/λB=(1-Pe) εz=k εz ,
其中,Pe为光纤的弹性光学系数;k=0.784,为波长变化的应变灵敏度系数.采用光纤光栅法,可以精确测量弯曲状态下单轴应变绝缘体上硅晶圆的应力.
考虑到单轴应变绝缘体上硅晶圆的对称性,选取了1/4晶圆的4个测试点,其中1、2、3号测试点的光纤光栅沿弯曲方向粘贴,4号测试点的光纤光栅则与应变分析呈45°角,如图6所示.
采用微光SM125型光纤光栅解调仪测试样品,光纤截面直径为 125 μm,杨氏模量E为 72 GPa.测试计算结果如表3所示.由表3可知,单轴张应变绝缘体上硅晶圆应力分布的光纤光栅实验计算结果与其ANSYS模拟结果基本一致.并且从表中可以发现,测试点1、2、3处的应力大小依次减小.这是由于点1和点2相比,对应测试点上沿直径方向的尺寸减小,使需要产生相同弯曲半径所需的弯曲力矩降低; 点1和点3相比,点3处于晶圆边缘,晶圆外侧区域很小,相应产生相同弯曲半径时对点3的作用力也更小; 而点4处利用光栅光纤法测试所得结果为晶圆弯曲方向及其垂直方向上应力的矢量和,由于单轴应变垂直方向上的应力很小,导致该方向上的应力最小.
表3室温下不同弯曲半径下张应变绝缘体上硅晶圆光纤光栅实验测试结果与计算结果
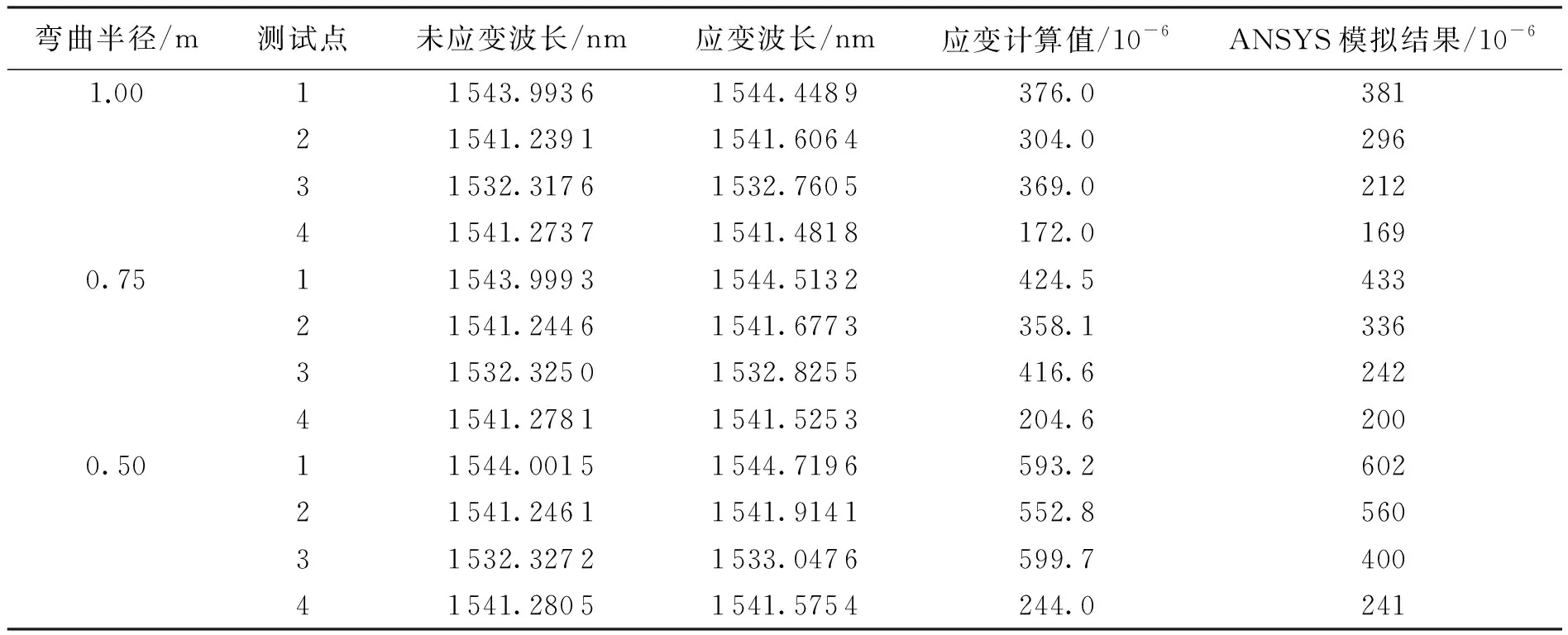
弯曲半径/m测试点未应变波长/nm应变波长/nm应变计算值/10-6ANSYS模拟结果/10-61.0011543.99361544.4489376.038121541.23911541.6064304.029631532.31761532.7605369.021241541.27371541.4818172.01690.7511543.99931544.5132424.543321541.24461541.6773358.133631532.32501532.8255416.624241541.27811541.5253204.62000.5011544.00151544.7196593.260221541.24611541.9141552.856031532.32721533.0476599.740041541.28051541.5754244.0241
4 结 束 语
根据弹性力学理论和绝缘层上单轴应变硅的工艺原理,笔者提出并建立了晶圆级单轴应变绝缘体上硅的有限元模型,对单轴应变绝缘体上硅晶圆的张应力和压应力的分布及变化趋势进行了系统的计算与分析.ANSYS模拟结果表明,在同样弯曲半径下,弯曲方向的应力最大,而垂直弯曲面方向的应力最小,且应力性质相反.因此,可将弯曲方向作为互补金属氧化物半导体器件的沟道方向; 而在不同弯曲半径下,应力随弯曲半径的减小而增加,但应力分布的均匀性却随弯曲半径的减小而降低.同时,单轴张应变绝缘体上硅晶圆应力分布的光纤光栅测试结果显示,其与ANSYS模拟结果基本一致,说明了文中模型的正确性与模拟结果的准确性.
参考文献:
[1] CHEN B W, CHANG T C, HUNG Y J, et al. Impact of Repeated Uniaxial Mechanical Strain on P-type Flexible Polycrystalline Thin Film Transistors[J]. Applied Physics Letters, 2015, 106(18): 183503.
[2] 戴显英, 王琳, 杨程, 等. 机械致单轴应变SOI晶圆的制备[J]. 西安电子科技大学学报, 2012, 39(3): 209-212.
DAI Xianying, WANG Lin, YANG Cheng, et al. Fabrication of the Uniaxial Strained SOI Wafer by Mechanical Bending[J]. Journal of Xidian University, 2012, 39(3): 209-212.
[3] DING Y J, CHENG R, ZHOU Q, et al. Strain Engineering of Ultra-thin Silicon-on-insulator Structures Using Through-buried-oxide Ion Implantation and Crystallization[J]. Solid-State Electronics, 2013, 83: 37-41.
[4] BESNARD G, GARROS X, ANDRIEU F, et al. Superior Performance and Hot Carrier Reliability of Strained FDSOI nMOSFETs for Advanced CMOS Technology Nodes[J]. Solid-State Electronics, 2015, 113: 127-131.
[5] DAI X Y, JI Y, HAO Y. A Growth Kinetics Model of Rate Decomposition for Si1-xGexAlloy Based on Dimer Theory[J]. Chinese Physics B, 2014, 23(1): 284-288.
[6] 戴显英, 郭静静, 邵晨峰, 等. CFD模拟RPCVD的正交法优化设计与分析[J]. 西安电子科技大学学报, 2013, 40(4): 72-78.
DAI Xianying, GUO Jingjing, SHAO Chenfeng, et al. Orthogonal Optimal Design and Analysis of RPCVD Simulation by CFD[J]. Journal of Xidian University, 2013, 40(4): 72-78.
[7] COQUAND R, CASSE M, BARRAUD S, et al. Strain-induced Performance Enhancement of Trigate and Omega-gate Nanowire FETs Scaled Down to 10-nm Width[J]. IEEE Transactions on Electron Devices, 2013, 60(2): 727-732.
[8] SHAO R W, GAO P, ZHENG K. The Effect of Tensile and Bending Strain on the Electrical Properties of p-type110Silicon Nanowires[J]. Nanotechnology, 2015, 26(26): 265703.
[9] HIMCINSCHI C, RADU I, MUSTER F, et al. Uniaxially Strained Silicon by Wafer Bonding and Layer Transfer[J]. Solid-State Electronics, 2007, 51(2): 226-230.
[10] DAI X Y, SHAO C F, HAO Y. Uniaxially Strained Silicon on Insulator with Wafer Level Prepared by Mechanical Bending and Annealing[J]. Applied Physics Express, 2013, 6(8): 081302.
Stresscalculationandanalysisofuniaxiallystrainedsiliconontheinsulator
MIAODongming1,2,DAIXianying1,2,WUShujing1,2,ZHAOTianlong1,2,SHAOChenfeng1,2,HAOYue1,2
(1. School of Microelectronics, Xidian Univ., Xi’an 710071, China; 2. State Key Lab. of Wide Bandgap Semiconductor Technology Disciplines, Xidian Univ., Xi’an 710071, China)
In order to study the wafer level uniaxial strained silicon insulation layer on the stress distribution and variation trend, a uniaxial strained SOI wafer is successfully fabricated by annealing in SOI mechanical bending at the wafer level, with the advantages of low cost and simple process. On this basis, the stress of mechanical induced uniaxially strained SOI wafers in various directions under different bending radii is simulated with ANSYS, and the results show that the stress along the bending direction, which is suitable for the channel of the COMS device, is much larger than that perpendicular to the bending direction. Also, the stress significantly increases and the uniformity of the stress distribution decreases with the decrease of bending radii. The stress distribution of the uniaxially strained SOI obtained by the optical fiber grating measurement is in good agreement with the ANSYS simulation results.
mechanical bending annealing; wafer level uniaxial strain; silicon on insulator; stress distribution; finite element analysis
2017-06-28
时间:2017-09-18
国家部委重点基金资助项目(9140A08020115DZ01024);高等学校学科创新引智计划资助项目(B12026)
苗东铭(1986-), 男,西安电子科技大学博士研究生, E-mail: miaodongming@126.com.
戴显英(1961-), 男,教授, E-mail: xydai@xidian.edu.cn.
http://kns.cnki.net/kcms/detail/61.1076.TN.20170918.1006.002.html
10.3969/j.issn.1001-2400.2018.01.029
TN30405;O35
A
1001-2400(2018)01-0162-06
(编辑: 郭 华)

