熔丝沉积成型中最优放置方向选择算法

魏潇然

(西北大学 新闻传播学院，陕西 西安 710127)

熔丝沉积成型中最优放置方向选择算法

魏潇然

(西北大学 新闻传播学院，陕西 西安 710127)

在熔丝沉积成型制造中，调整物体放置方向可以改善制造后模型表面精确度，并能有效减少打印耗材和打印时间．但是现有最优放置角度算法很少兼顾这三因素．文中在考虑这三因素的基础上，同时分析人们对显著特征区域精细程度主观观感的不同，以及去除支撑时对模型的损害，提出了支撑体积耗材、模型表面打印耗材、打印时间、模型表面精细度、模型表面显著特征加权精细度、支撑覆着表面积等6项成型指标与放置角度的关系函数，并根据这6项成型评价指标函数构造最优放置角度目标函数；最后，求解最优化目标函数以获取最优放置角度．实验结果表明，该算法可有效计算各种条件下的物体最优放置角度，优化了制造物体表面的精确度，节约了打印耗材和打印时间，避免了部分后处理对模型造成的损害．

快速成型;熔丝沉积成型;打印放置方向

三维(3-Dimensional，3D)打印是快速成型领域中的革命性技术，在工业设计、制造业、医学、建筑等领域已有广泛的应用．熔丝沉积成型技术[1]是3D打印中最常用的技术之一．在熔丝沉积成型制造前，调整物体放置角度可以改善制造后模型表面精确度，并能有效减少打印耗材和打印时间．关于3D打印以及熔丝沉积成型中的放置角度算法已有大量研究．

上世纪90年代起，已有许多学者对3D打印物体的放置角度选取进行研究．文献[2]首先分析定义了受不同放置角度影响的打印成型指标，包括模型高度、支撑结构体积和模型表面台阶效应，给出了这些指标的计算方法，并选择在若干个不同角度下计算这些指标，选择其中的最优放置角度．许多学者利用智能算法对该问题求解，文献[3]通过估计打印时间、后处理时间和平均表面粗糙度构造了一个多目标的适应度评价函数，利用遗传算法求解最优放置角度．文献[4]将球极坐标系下两个角度参数作为基因编码，构造遗传算法，对打印高度、台阶效应和打印耗材构造适应度函数，使用遗传算法求解，计算最优放置角度．另有学者专门研究打印放置角度对单项成型评价指标的影响，文献[5]利用图形处理器对深度图像的快速计算能力，提出了一种基于深度图像的快速支撑结构体积计算方法，并通过遍历各放置角度寻找支撑结构最小的打印放置角度．文献[6]分析了圆柱度公差与打印放置角度的关系，提供可视化工具，用于求解多圆柱特征模型的最优放置角度．也有学者将放置角度的选择和其他算法或需求结合起来进行研究，文献[7]结合人为主观对显著区域及优先视点的分析，计算旋转放置角度，使得支撑结构附着在非显著区域，避免去除支撑时对模型的损坏．文献[8]将模型分割与最优旋转放置角度相结合，将分割后模型的表面法向量尽可能地与打印方向垂直，使得分割后各子模型打印精度最高．许多学者通过确定放置角度，减少支撑结构耗材[9-11]．文献[9]计算待支撑面积最小的旋转放置角度，并在此角度下构造了省材的树形结构有效支撑模型悬空表面．

打印视角存在一个重要问题: 就是受打印放置视角影响的多个指标其最优角度可能相差很远，有时甚至是相悖的，例如减少支撑结构的旋转角度可能反而增加了物体表面的粗糙度，现有算法只考虑少数几个指标最优，会造成在提高模型某成型指标的同时，却降低了其他成型指标．

笔者针对熔丝沉积成型，提出外部支撑体积的快速方法、模型打印时间耗材快速估算方法、支撑附着表面积计算方法以及模型精确度、显著特征度粗糙度计算方法，并建立起这些成型指标和旋转放置角度的关系函数，构造最优放置角度目标函数，求解最优化问题，以选择最优放置视角．实验证明，利用该方法以最优放置角度打印模型，可大大提升模型的精细度，并有效减少模型打印耗材与模型打印时间．

1 最优角度选择算法

1.1 问题描述

首先分析打印放置角度与模型各成型指标间的关系．

(1) 放置角度与外部支撑结构的关系．在不同放置角度下，模型打印所需的外部支撑会发生变化，这是由于改变放置角度，每层打印切片的形态均会发生变化，各层切片需要支撑的悬空面积也会随之变化．如图1所示，在不同角度下，外部支撑体积差异很大，选择外部支撑结构体积相对较小的放置角度，可以有效节约打印外部支撑的耗材以及时间．

(2) 放置角度与支撑附着面积的关系．现有熔丝沉积成型技术中，通常采用与制造材料相同或相近的材质作为外部支撑，旋转模型改变外部支撑结构的同时，也改变了支撑结构所附着的模型表面区域，通过旋转模型角度来减少支撑附着面积，能在一定程度上减少去除支撑对模型造成的不必要损坏．

图1 不同放置角度下的外部支撑图2 台阶效应

(3) 放置角度与模型表面精确度的关系．熔丝沉积成型本质是一种分层制造技术，其各层间的台阶效应(如图2所示)是主要影响其表面精确度的因素，各层间倾角越小，其台阶效应越明显．旋转模型的打印放置角度，可以改变各层间的倾角，改善模型台阶效应．

图3 不同放置视角打印耗材差异

(4) 放置角度与显著特征精确度的关系．同样程度台阶效应在同一模型不同局部给人的感观是不同的，主观观测会更注重模型特征显著区域，对其精确度要求也较高．在某些应用场景下(如模型展示应用中)，期望显著特征较细致，而部分非显著特征可以适当粗糙，故计算时可将特征显著度加权，在整体精细程度变化不大的前提下，选择显著特征更精细的打印角度．

(5) 放置角度与模型打印时间、打印耗材的关系．在不同的放置角度下，模型的打印耗材与打印时间也会发生变化，一部分原因是由于外部支撑结构体的改变，另一部分原因是由于在模型各层壁厚相同情况下，同一曲面，倾角越大，需要打印的层数越多，耗材也越多．如图3所示，打印壁厚为常量，并且模型顶层、底层与模型侧壁厚度一致，左右两图中AD边、DC边和BC边分别平行或垂直于打印托盘，其打印耗材相同; 但是在AB边上，左侧模型要多打印两层，因每层壁厚相同，故左图需要耗费更多材料，相应的耗时也更多．合理调整模型放置角度，能有效节省模型表面打印材料和打印时间．

1.2 各指标的最优放置角度选择算法

对文中使用的坐标系进行定义，对打印空间建立笛卡尔坐标系，其中坐标y轴垂直于打印托盘，z轴朝向屏幕外，坐标系原点为打印托盘左后方点．模型的放置角度可以表示为(α，γ)，表示模型从初始位置绕x轴旋转角度α，然后绕z轴旋转角度γ．α和γ旋转区间均选择为[0，π]，即可覆盖所有放置角度解．

1.2.1 外部支撑耗材快速计算方法

当模型某网格i法向量Ni(ai，bi，ci)与y轴正方向夹角超过临界角度θ时，认定该处表面为悬空表面，需要添加支撑，文中设该临界角度为 π/2．则当模型表面某网格朝向模型外的法向量与y轴正方向夹角在(0，π/2] 区间时，该表面网格需要添加外部支撑．

(1) 将模型所有网格按照重心由高至低进行排序为M(m0， …，mn)，初始取i=0，计算mi在打印托盘平面上的投影si，mi为网格i的面积．计算mi到打印托盘所需要的支撑体积vi，vi为si面积乘以面片重心距打印托盘的距离．根据

(1)

计算mi与y轴的夹角，判断mi是否需要支撑．

(2) 若mi需要支撑，支撑体积V更新为V+vi．

(3) 若mi不需要支撑，则判断mi在打印托盘上的投影是否在(m0， …，mn)打印托盘的投影内，若在投影内，则支撑体积V更新为V-vi；若不在投影内，则支撑体积不变．若i≠n，i=i+1，则重复执行步骤(1)；若i=n，则返回V作为模型的外部支撑体积．

1.2.2 支撑附着面积计算

对于需要支撑的面片，可以计算其面积作为支撑附着面积．模型支撑附着表面积的计算公式为

(2)

下面分析模型旋转后，支撑附着面积的计算方法．

计算旋转后的法向量，并将其代入式(2)，可以获得当模型绕x轴旋转α，之后绕z轴旋转γ时，其对应的支撑附着面积为

(4)

1.2.3 模型表面精确度(台阶效应)评价方法

对台阶效应进行分析．如图2所示，梯形的斜边为实际模型表面，而斜边内侧阶梯状边为熔丝分层堆积形成的打印模型表面，由于熔丝沉积成型分层制造特点，该表面熔丝堆积呈现台阶状，与实际模型表面有一定差异．尖高(Cusp Height)h可以作为台阶效应的量化评价指标．尖高计算公式为

(5)

其中，l为层厚，cosθ为模型表面法向量与y轴正方向的夹角．

对于一个网格i，其上任意一点的尖高均为该网格法向量Ni(ai，bi，ci)与y轴正方向的夹角的绝对值，度量一个网格的表面精确度Hi，直接用该网格面积si乘以尖高即可．该网格绕x轴旋转α，并绕z轴旋转γ后，网格表面精确度计算为

(6)

模型整体的尖高为各网格面片尖高之和，模型上网格面片总数为n，模型绕x轴旋转α并绕z轴旋转γ后的整体尖高为

(7)

1.2.4 特征加权的精确度评价方法

高斯曲率可以反应模型某顶点潜在曲面的弯曲程度．文中将高斯曲率作为特征显著程度的评价指标，采用Meyer的Voronoi方法估算曲率．

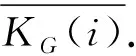
利用高斯曲率对各面片的精确度加权，以表示各面片的显著特征精确度．面片mi的显著特征精确度Sai(α，γ)和模型整体表面的显著特征精确度Satotal(α，γ)的表达式为

(8)

其中，k为常量，用于对表面弯曲分布不同的模型进行高斯曲率权重的调节．例如若模型呈现部分区域高斯曲率很大(平坦部分高斯曲率小于1，弯曲部分高斯曲率远大于1)，可以将k设置大于1，控制这些过大曲率．

1.2.5 打印耗材与打印时间计算方法

设模型一网格面片mi的表面积为si，其法向量Ni与y轴正方向的夹角为θ．根据余弦公式计算该夹角角度，进而计算其正弦值．任意网格的打印耗材的计算公式如下:

(9)

利用式(3)可计算模型绕x轴旋转α，绕z轴旋转γ后的θ，旋转后的表面耗材的计算公式为

(10)

外部支撑体积受旋转影响，但外部支撑始终垂直于打印平台，故外部支撑打印耗材可以直接根据体积计算．设喷头挤出速度为p，外部支撑为MS(α，γ)，则模型绕x轴旋转α，绕z轴旋转γ后的打印时间为

T(α，γ)=(M(α，γ)+MS(α，γ))/p．

(11)

1.3 求解最优放置角度

首先将这6大成型指标分类，可以分为3类: 第1类为打印消耗，其中包括模型表面打印耗材、支撑打印耗材和打印时间，这里估算的打印时间与模型表面打印耗材加上模型支撑耗材之和成正比，故之后进行最优化计算时，可以直接调整打印耗材与支撑耗材的权重即可将打印时间纳入计算中；第2类为表面精确度计算，其中包括模型表面精确度和显著特征加权精确度，显著特征精确度是对模型表面精确度进行曲率加权后的计算结果，可以将两类精确度计算公式合并表示；第3类为后处理代价计算，文中后处理仅考虑去除支撑的代价，即支撑在模型表面的附着面积．

选择最优打印放置角度时，可以根据需求进行选择(例如耗时最少，精度最高，后处理最简便)，选择三类指标中的某一项; 也可以同时考虑三类指标，由于三类指标均是越低越优，直接对其加权生成最优化目标函数，其公式如下:

min(C1(Ms(α，γ)+M(α，γ))+C2(Htotal(α，γ)+C21Satotal(α，γ))+C3S(α，γ)) ,

(12)

其中，C1为模型打印耗材耗费权重，C2为模型表面精确度权重，C21为模型表面显著特征精确度权重，C3为模型后处理代价权重．随着模型的变大，模型外部支撑耗材增加幅度远大于模型表面精确度和支撑附着面积等其他成形指标．这是因为与外部支撑计算体积相关，是三维空间中的度量; 而精确度、附着面积等均与面积相关，是二维空间中的度量，虽然模型表面耗材也是体积，但是它是由表面积乘以常量的形式计算获得的，故其也可以算作与面积相关．如果对其均用线性加权，则物体越大，外部支撑对目标函数的影响会越大，影响最终最优放置位置．故对最优化目标函数进行优化，优化后的目标函数为

min(C1(Ms(α，γ)3/2+M(α，γ))+C2(Htotal(α，γ)+C21Satotal(α，γ))+C3S(α，γ)) ．

(13)

观察上述各成型指标在不同旋转角度下计算公式可知，对于一个确定模型，这些公式变量均仅为(α，γ)，故最优放置视角问题的解可以表示为一个二维方向向量(α，γ)．优化算法仅需在二维解空间中搜索即可．最优化目标函数为存在多个一类间断点的无约束优化函数．

文中使用改进的Powell方法(Sargent形式)对最优打印放置角度进行计算，求解获得最优放置角度．

文中算法具体流程如图4所示．输入三维网格模型和打印参数，首先计算模型各网格的法向量与顶点曲率；之后生成各方向的模型打印相应指标计算函数，并构造最优化目标函数；最后求解获得最优放置方向．

图4 文中算法流程图

2 实验结果与分析

文中实验运行机器配置中央处理器(Central Processing Unit，CPU)为Intel Xeon(R) E5-2650@2.00 GHz，内存为 32 GB，图形处理器(Graphics Processing Unit，GPU)为NVDIA Quadro6000．模型打印使用的是Makerbot Replicator 2X型号的3D打印机．打印使用材料为丙烯腈-丁二烯-苯乙烯塑料(Acrylonitrile Butadiene Styrene plastic，ABS)，配置参数为打印层高 0.2 mm，模型壁厚为2层熔丝，打印速度为 90 mm/s，喷嘴空驶速度为 120 mm/s．

图5 最优放置位置打印结果示例

文中实验选取材料为ABS塑料，其材料密度ρ=1.05 g/cm3，壁厚t=2．若用户选取密度不同的材质或壁厚，则需对C1权重进行调整，若ρ大于文中材料密度，或t大于文中选取的壁厚，则C1取值减小; 若ρ小于文中材料密度，或t小于文中选取的壁厚，可适当提高C1取值．C1取值区间为[0.2，1.0]，C2取值区间为[0.5，2.0]，C21取值区间为[0.5，2.0]，C3取值区间为[0.2，2.0]，可根据具体需求调节权重取值．图5为不同需求下模型的最优打印角度选择，图5(a)、(e)、(i)为耗材较优打印放置角度，图5(b)、(f)、(j)为表面精度较优打印放置角度，图5(c)、(g)为后处理代价较优打印放置角度，图5(d)、(h)、(k)为各指标加权较优打印放置角度．表1为实验统计数据， 其中，#b表示模型打印包围盒尺寸， #t表示模型打印时间，#m表示模型打印耗材，#sm表示模型精确度，#sa表示支撑结构附着面积．

表1 算法实验数据统计

3 总结展望

以上分析了打印模型放置角度对模型成型各因素的影响，构造模型旋转放置角度与支撑结构、打印耗材、打印时间、表面粗糙度、显著特征粗糙度、支撑附着面积的关系公式，并构造最优放置角度目标函数，利用改进的Powell方法求解该最优化函数，获得最优放置视角．最后根据实验结果和实际应用中的具体需求，分析了最优化目标函数中各因素权重的选择，并根据实际需求构造了带约束的最优放置目标函数．实验结果表明，利用文中方法可有效计算各种需求条件下的物体最优放置角度，优化了制造物体表面精确度，节约了打印耗材和打印时间，避免部分后处理对模型造成的损害．

文中列举的各成型指标计算公式均是针对熔丝沉积成型基本原理和基本算法进行分析的，但在实际应用中，这些成型指标在打印时已有相应的优化算法，例如，具体支撑结构生成算法不会使支撑占用待支撑空间的全部体积，具体扫描线和切片算法已经对台阶效应进行了相应优化调整．针对实际场景计算旋转放置角度时，应将这些优化算法的因素也考虑进去．这也是后续的研究方向．

参考文献：

[1] 刘利刚, 徐文鹏, 王伟明, 等. 3D打印中的几何计算研究进展[J]. 计算机学报, 2015, 38(6): 1243-1267.

LIU Ligang, XU Wengpeng, WANG Weiming, et al. Survey on Geometric Computing in 3D Printing[J]. Chinese Journal of Computers, 2015, 38(6): 1243-1267.

[2] ALEXANDER P, ALLEN S, DUTTA D. Part Orientation and Build Cost Determination in Layered Manufacturing[J]. Computer Aided Design, 1998, 30(5): 343-356.

[3] CANELLIDIS V, GIANNATSIS J, DEDOUSSIS V. Genetic-algorithm-based Multi-objective Optimization of the Build Orientation in Stereolithography[J]. International Journal of Advanced Manufacturing Technology, 2009, 45(7/8): 714-730.

[4] PHATAK A M, PANDE S S. Optimum Part Orientation in Rapid Prototyping Using Genetic Algorithm[J]. Journal of Manufacturing Systems, 2012, 31(4): 395-402.

[5] EZAIR B, MASSARWI F, ELBER G. Orientation Analysis of 3D Objects toward Minimal Support Volume in 3D-printing[J]. Computers and Graphics, 2015, 51(6): 117-124.

[6] PAUL R, ANAND S. Optimal Part Orientation in Rapid Manufacturing Process for Achieving Geometric Tolerances[J]. Journal of Manufacturing Systems, 2011, 30(4): 214-222.

[7] ZHANG X, LE X, PANOTOPOULOU A, et al. Perceptual Models of Preference in 3D Printing Direction[J]. ACM Transactions on Graphics, 2015, 34(6):1-12.

[8] WANG W M, ZANNI C, KOBBELT L. Improved Surface Quality in 3D Printing by Optimizing the Printing Direction[J]. Computer Graphics Forum, 2016, 35(2):59-70.

[9] VANEK J, GALICIA J A G, BENES B. Clever Support: Efficient Support Structure Generation for Digital Fabrication[J]. Computer Graphics Forum, 2014, 33(5):117-125.

[10] 魏潇然, 耿国华, 张雨禾. 3D打印中的模型去支撑划分方法[J]. 西安电子科技大学学报, 2016, 43(2): 180-185.

WEI Xiaoran, GENG Guohua, ZHANG Yuhe. Partition Model into 3D-printable and No Supporting Parts[J]. Journal of Xidian University, 2016, 43(2): 180-185.

[11] ZWIER M P, WITS W W. Design for Additive Manufacturing: Automated Build Orientation Selection and Optimization[J]. Procedia CIRP, 2016: 128-133.

Optimalprintingdirectionselectioninfuseddepositionmodeling

WEIXiaoran

(School of Journalism and Communication, Northwestern Univ., Xi’an, 710127, China)

In Fused Deposition Modeling (FDM) manufacture, adjustment of the object printing direction can improve the surface accuracy of the manufactured model, and can effectively reduce the printing time and printing material. However, the existing algorithm seldom takes account of all these factors. Considering these three factors and analyzing the people’s subjective perception of the precision of the salient features and the damage caused by removal of the supporting, we propose the relationship functions among printing direction, support structure material, model surface printing supplies, printing time, model surface accuracy, salient features of precision and the processing cost of the model. According to these functions of the six evaluation indexes, the optimal printing direction objective function is constructed, and is solved to obtain the optimal printing direction. Experimental results show that the algorithm can be used to calculate the optimal printing direction of the object in various conditions, optimize the accuracy of the surface of the object, save the printing material and printing time, and avoid the damage caused by the post processing.

rapid prototyping; fused deposition modeling(FDM); printing direction

2017-02-23

时间：2017-06-29

国家自然科学基金资助项目(61373117)

魏潇然(1987-)，男，讲师，E-mail：wxran1987@163.com．

http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1735.036.html

10.3969/j.issn.1001-2400.2018.01.018

TP391

A

1001-2400(2018)01-0099-07

(编辑： 齐淑娟)